基于优化算法的2-bit编码超表面缩减RCS研究

董妮娅,张伟男,林 峰,谭沐莹

(1.重庆移通学院 公共大数据安全技术重庆市重点实验室,重庆 401520;2.重庆邮电大学 通信与信息工程学院,重庆 400065;3.重庆邮电大学 自动化学院,重庆 400065)

0 引言

近年来,各种人工新型材料被应用于宽带雷达散射截面(RCS)的缩减。编码超表面作为一个新兴的研究领域,为实现RCS的缩减提供了新的思路[1-2]。不同的编码序列对应的散射特性均不同,规则编码的散射特性也是规则的。当编码呈现无规律性时,散射特性会杂乱无章地发散至多个方向,根据能量守恒可知,每束散射波的能量都会变小,从而实现RCS的缩减。利用超表面实现RCS具有方法多,设计灵活等优点,是最常用的实现RCS缩减的方法[3-4]。

相位梯度超表面是一种亚波长尺寸的各向异性结构,能够使入射电磁波发生相位突变,在沿其表面切线方向产生相位梯度[5],并以此控制反射波或者透射波的传播方向。由于相位梯度超表面具有灵活控制波束方向的性能,可将反射波沿着非入射方向进行汇聚,从而减小入射方向上的RCS缩减。利用相位梯度超表面可以控制指定方向上的RCS,应用范围更广。

传统的超表面设计过程通常包括模型设计、参数扫描和优化。此过程还需数十次甚至数百次电磁仿真,既耗时又消耗计算资源,所以需要研究优化算法来对编码矩阵进行合理设计[6]。

1 相位梯度超表面单元设计

图1为单元结构图。由图1(b)可见,该单元结构由3层结构组成。中间层结构为介质层,选用的介质基板为FR-4(lossy),介质层厚度为h,其相对介电常数为4.3,损耗正切值为0.002。顶层、底层结构为金属层,金属部分为铜,其电导率(σ)为5.8×107S/m,厚度(d)为0.018 mm。金属层结构采用图1(a)所示的对称的 “十”字和半圆环结构的组合,图中L代表金属臂长,wm代表金属臂宽,p代表单元的周期边长,rin、rout分别代表内外圆的半径。

图1 PGM的单元结构模型示意图

通过使用控制变量的方法,改变金属臂长L单个参数来改变反射相位,并采用仿真软件CST对不同的单元结构参数进行扫描优化仿真。符合设计要求的4个单元结构的反射振幅特性和反射相位图如图2所示。由图可见,以频率14.42 GHz为中心,选择4组优化的参数L值,分别为3.59 mm、4.44 mm、5.00 mm、7.40 mm,使其在频率13～20 GHz都有较显著的相位梯度。

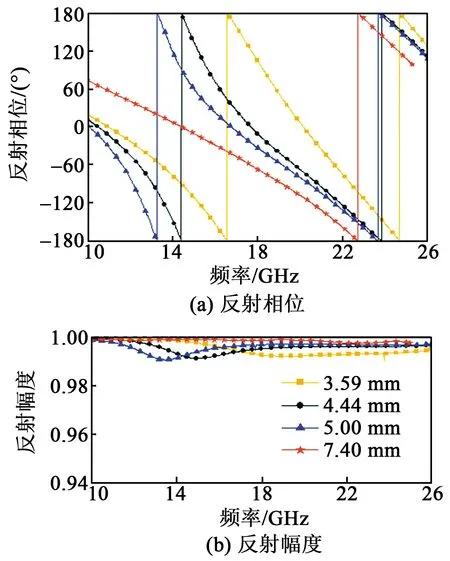
图2 4个基本单元的幅频特性图

由图2(a)可见,当L=5.00 mm时,在14.42 GHz处的反射相位值为90.17°,基本上可看作是90°;当L分别为7.40 mm,4.44 mm,3.59 mm时的相位值分别为 0.01°,179.78°,-89.88°。

由图2(b)可知,这4个单元结构在14.42 GHz处的幅值近似为1,反射相位差大致为90°,满足2-bit数字编码超表面的设计指标要求。详细的单元结构编码、几何参数值和对应的相位值如表1所示。设计完成2-bit编码超表面单元结构后,可以利用这4个结构进行后续的阵列研究。

表1 单元结构对应的编码表

2 优化算法设计

为了得到数字编码超表面的最佳缩减性能,将粒子群算法和遗传算法与常用在天线阵列的计算方法阵列模式综合(APS)相结合,得到一种改进的优化算法GAPSO-APS算法。

2.1 优化算法设计

在某一个N维的搜索空间中,存在种群规模为M的粒子群,其中第i个粒子在时刻t的状态由速度和位置两个向量表示。

在t时刻,第i个粒子的速度信息、位置信息分别表示为

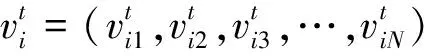
(1)

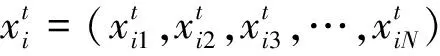
(2)

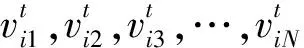
由于散射特性问题是一个连续性的问题,而采用2-bit编码量化是一个离散化问题,故考虑在完成一次种群遍历后,对算法求得的最优解进行一次最优解的邻域寻优判别过程,以此来进一步提高GAPSO-APS算法的全局寻优能力。

(3)

(4)

(5)

根据上述理论,在t+1时刻,种群中的每个粒子对应的速度和位置更新公式定义如下:

(6)

(7)

式中:w为惯性权重;t为当前种群的迭代次数;r1,r2,r3是介于0～1的随机数;c1,c2,c3c1,c2,c3分别为认知参数、社会远域参数和社会邻域参数,一般取c1=c2=c3∈[1,2.5]。

式(6)可以理解为粒子的下一步迭代的移动方向=惯性方向+个体最优方向+群体最优方向+邻域最优方向。

GAPSO-APS算法流程图如图3所示,算法具体实现过程如下:

图3 GAPSO-APS算法流程图

a) 程序开始。根据所求解的问题,对所搜索变量进行编码规则设定,进行程序参数的初始化。

b) 求解区域中所有个体的适应度值,并分类优劣种群,完成速度和位置更新。

c) 利用遗传操作处理“劣种群”,选择进化后的优势个体作为下一代。

d) 所有粒子在本轮寻径结束后,将所有路径作为一个种群进行选择、交叉、变异、再选择,得到本轮最优,再进行邻域寻优,计算适应度值。

e) 判断目前的迭代次数是否达到设置的终止条件。如果达到,则跳出循环。

在完成速度和位置更新操作后,评估本次迭代的适应度值。按照从高到低的顺序,将种群分为“优种群”和“劣种群”,并对这两类种群分别采取不同的进化迭代策略。“劣种群”通过遗传算法的交叉变异操作产生子代,再次评估对应的适应度函数值,若有适应度值高于优种群的,采取按位递补的方法替换优种群。“优种群”则在内部采取末位淘汰的方法,从而产生适应度相对较高的、新的种群进行下一次迭代。

借助Matlab-CST进行联合仿真,每条路径可视为随机排布的矩阵。2-bit编码超表面的阵列散射场函数可表示为

kDsinθ[(m-1/2)cosφ+(n-

1/2)sinφ}}

(8)

式中:θ和φ分别为电磁波的俯仰角和方位角;fs(θ,φ)为单个阵元的辐射强度值;k=2π/λ;φ(m,n)代表第m行、第n列所在的编码单元的反射相位;D为单个编码单元的周期。

由于算法优化的目标是远场散射函数的最大值越小越好,所以选择最符合问题的GAPSO-APS算法适应度函数为

fitness=min(max(f(θ,φ)))

(9)

2.2 改进的算法在编码超表面的仿真与分析

采用2.1节介绍的优化算法,在Matlab中经过算法优化后得到的编码矩阵的最终序列为

编码矩阵序列构建1个相位梯度超表面,由8×8个超级子单元组成。两个相位不同的单元之间会发生电磁耦合效应,为了避免这种现象,引入2×2的子单元来减小耦合。将第1节设计的4种2-bit编码单元结构使用CST仿真软件,按照优化后的编码矩阵进行建模,最终得到的相位编码超表面如图4所示。在全波仿真软件CST中分别构建相位梯度超表面和同面积的金属板,并进行对比仿真。为了验证优化后的超表面的RCS性能,将其与金属板进行对比,超表面RCS缩减性能如图5所示。

图4 CST构建的优化超表面

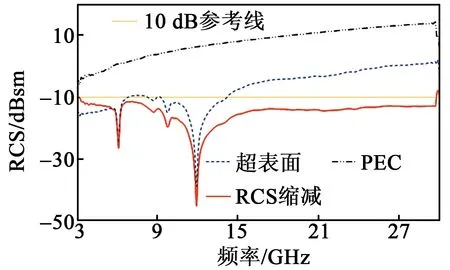
图5 算法优化后的RCS缩减性能

由图5可见,与金属板相比,优化后的超表面具有频率3.1～29.7 GHz的低散射特性。在该频率内,RCS的缩减值都高于10 dB,最大缩减在11.9 GHz时达到45.03 dB,RCS缩减相对带宽达到162%。仿真得到的三维远场方向图如图6所示。金属板具有恒定的反射相位,图6(b)中可以看到强反射。而对于优化的超表面(见图6(a)),由于表面阵列间的多次反射,主瓣能量被搬移到其他非法线方向,从而有效降低了RCS。

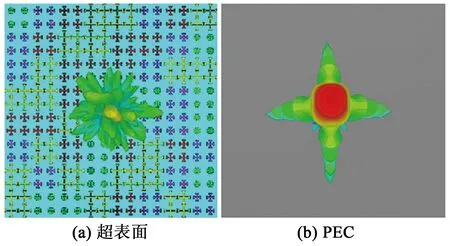
图6 超表面与金属板在11.9 GHz远场散射图

3 结束语

本文提出了一种应用于超表面编码矩阵优化的GAPSO-APS算法,利用算法快速生成的相位矩阵构建的超表面具有较小的RCS值。通过Matlab-CST联合仿真验证了该算法的收敛性能优于传统算法,将其应用于设计的2-bit 相位梯度超表面,实现了更高精度的RCS缩减。仿真结果表明,在3.1～29.7 GHz频带内都能实现很好的RCS缩减,相对带宽高达到162%,最大RCS缩减值达到45.03 dB,进一步验证了算法的有效性。