高品质因数压电驱动氮化铝基悬臂梁微谐振器

石 帅,杨清瑞,原 毅,李浩霖,牛鹏飞,刘伯华,张孟伦

(天津大学 精密测试技术及仪器国家重点实验室,天津 300072)

0 引言

悬臂梁微机电谐振器作为微机电系统(MEMS)中最重要的基础器件之一,其具有结构简单、易加工、频率范围广等优势,被广泛应用于质量传感器[1]、生物化学传感器[2-4]、原子力显微镜(AFM)[5]、能量采集器[6-7]、振荡器[8]及声学[9-10]等领域。悬臂梁谐振器的主要驱动方式分为静电驱动[11-12]和压电驱动[8-9,11,13-14]两种。静电驱动谐振器可实现高品质因数(Q),但前提是提供较大的直流偏置电压和较小的电容间隙,这在一定程度上限制了静电驱动谐振器的应用场景。近年来,压电驱动谐振器因具有驱动电压低、响应速度快、噪声小等优势而受到学术界广泛关注。

压电驱动悬臂梁谐振器主要有两种基础工作模态:面内弯曲振动模式和面外弯曲振动模式。在基于压电薄膜的悬臂梁结构中,悬臂梁的厚度一般小于宽度,悬臂梁谐振器的面外弯曲振动模态受到的模式干扰最少,一般具有更高的Q值[15]。面外弯曲振动模式的压电悬臂梁,常见的层叠结构从下至上依次是支撑层/底电极/压电层/顶电极[16],而当前主流的支撑层材料为单晶硅[14],在现有研究中表现出较高的Q值。压电驱动硅基悬臂梁谐振器通常需要在绝缘体上硅(SOI)衬底或包含预埋空腔的SOI(Cavity SOI)衬底上进行加工。在SOI衬底上进行加工时,通常需要对背部支撑硅层进行深硅刻蚀,从而使悬臂梁悬空,但存在加工难度较大而导致的良率受限,同时不利于实现器件的进一步真空封装,进而限制了此器件在传感器中的应用。使用Cavity-SOI衬底加工能够避免上述工艺步骤,但Cavity-SOI通常需要根据每种器件进行定制,因此制造成本较高。

相较于锆钛酸铅(PZT)、氧化锌(ZnO)、铌酸锂(LiNbO3)和钽酸锂(LiTaO3)等压电材料,氮化铝(AlN)具有高声速、低弹性温度系数、高导热性及低材料损耗等优势[17],近年来成为谐振式微谐振器中常用的薄膜压电材料。如Fabian等设计了基于AlN支撑层的梁式结构谐振器,并将其应用于加速度计[18],但并未开展针对该层叠结构谐振器的性能研究。Yuan等研究了以AlN作为支撑层的面内弯曲振动模式的音叉谐振器[19]。

本文以悬臂梁谐振器为基础,设计了一种以AlN为压电层和支撑层材料,工作在面外弯曲振动模式的压电悬臂梁谐振器,并完成了该谐振器的加工和测试。该结构能够有效降低加工难度,且易与互补金属氧化物半导体(CMOS)电路集成,有利于获得更高集成度的MEMS系统。通过理论分析研究了固定频率下谐振器品质因数与器件尺寸的关系,并对比了AlN和硅两种支撑层材料对谐振器品质因数的影响,证明了该层叠结构能够在缩小器件尺寸的同时保持高品质因数。综合考虑性能和加工难度,本文确定了合适的器件尺寸。通过实验研究了电极尺寸对在真空中谐振器性能的影响,从而确定了工作在面外弯曲振动模式的压电驱动氮化铝基悬臂梁谐振器的最优设计。

1 谐振器的设计及仿真

1.1 谐振器基本结构

本文研究的工作在面外弯曲振动模式的氮化铝基悬臂梁谐振器的层叠结构如图1(a)所示。图中谐振器以较厚的AlN为支撑层,压电层材料为AlN,电极材料为钼。图1(b)为该谐振器的俯视图,图中LC、WC分别为悬臂梁的长度和宽度,LE、WE为顶电极的长度和宽度。驱动谐振器工作时,谐振器的顶电极和底电极分别连接信号端和接地端,其面外弯曲振动模态如图1(c)所示。

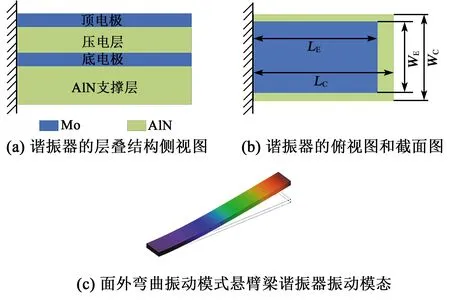
图1 氮化铝基悬臂梁谐振器结构设计及振动模态

1.2 理论分析

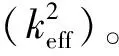
悬臂梁谐振器的谐振频率[20]:

(1)

式中:ω0为悬臂梁谐振器的谐振角频率;E为材料的杨氏模量;I=(wt3)/12为悬臂梁在振动方向上的转动惯量,w为悬臂梁的宽度,t为悬臂梁的厚度;ρ为材料的密度;A为悬臂梁的截面面积;l为悬臂梁的长度;an为由边界条件决定的常数,对于单端固支的悬臂梁谐振器,an=1.875。由式(1)可知,工作在面外弯曲振动模式的悬臂梁谐振器,其谐振频率与厚度成正比,与长度的平方成反比。

谐振器的Q值能够直观反映器件中的能量损耗情况,是衡量谐振器性能的重要参数。Q值影响到谐振器的频率准确性和稳定性,较高的谐振器Q值有利于实现具有较高检测灵敏度和较高信噪比的传感器。谐振器的总Q值可以通过各种能量损耗对应Q值之和进行定义:

(2)

式中:Qanc表示锚点损耗所决定的Q值;QTED表示热弹性阻尼损耗所决定的Q值;Qair表示空气阻尼损耗所决定的Q值;Qothers表示其他损耗因素所决定的Q值,包括材料损耗、界面损耗等。

本文研究的悬臂梁谐振器主要测试和工作条件为真空环境,因此,空气阻尼可忽略,而锚点损耗和热弹性阻尼是影响和决定悬臂梁谐振器Q值的最主要因素。本节将针对这两种损耗机理对氮化铝基和硅基的悬臂梁谐振器的影响展开对比分析,相关材料参数[21-22]如表1所示。

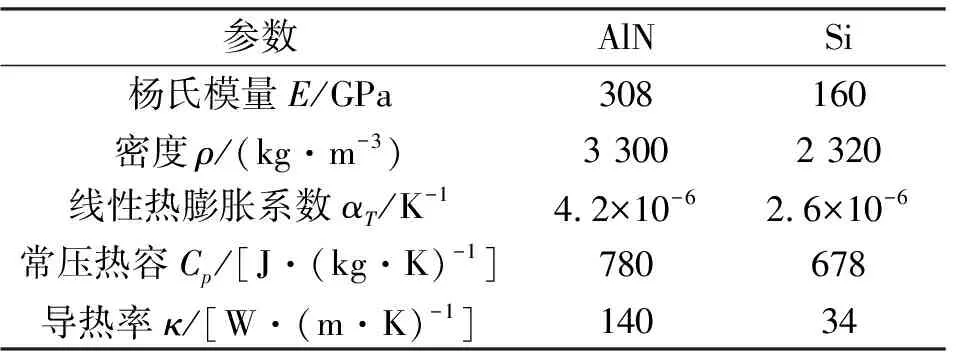
表1 AlN与Si相关材料参数

锚点损耗是振动能量以弹性波的形式通过锚固点扩散至基底导致的能量损耗。悬臂梁谐振器的Qanc[23]为

(3)

式中ts为悬臂梁谐振器支撑层的厚度。将其代入式(1),可得Qanc与悬臂梁的长度、谐振频率的关系:

(4)

通过式(4)可推导出在悬臂梁谐振器频率保持不变的情况下,Qanc与l3呈反比关系,且随着长度的缩短而有明显提高。根据式(1)的推导,当悬臂梁长度缩短时,为保持频率不变,需要同时减小悬臂梁谐振器的厚度。因此,悬臂梁谐振器的小型化不仅可以提高系统集成度,还能显著提高其Qanc值。

式(4)适用于单一材料所构成的悬臂梁结构,虽然本文的悬臂梁结构中还存在用于驱动的电极材料,但电极材料的厚度占比仅为8%,故在计算中近似使用了单一材料的模型。分别将AlN和Si的材料参数代入式(4),得到不同谐振频率下悬臂梁谐振器的Qanc与长度的关系如图2(a)所示,其中A、B、C分别对应固定频率为30 kHz、60 kHz、90 kHz的氮化铝基悬臂梁,D、E、F分别对应固定频率为30 kHz、60 kHz、90 kHz的硅基悬臂梁。图中上坐标轴列出了在对应谐振频率和长度下悬臂梁的厚度。由图可见,在相同谐振频率和长度下,氮化铝基谐振器的厚度比相应硅基谐振器的厚度约低14%,同时氮化铝基谐振器的Qanc略高于硅基谐振器。

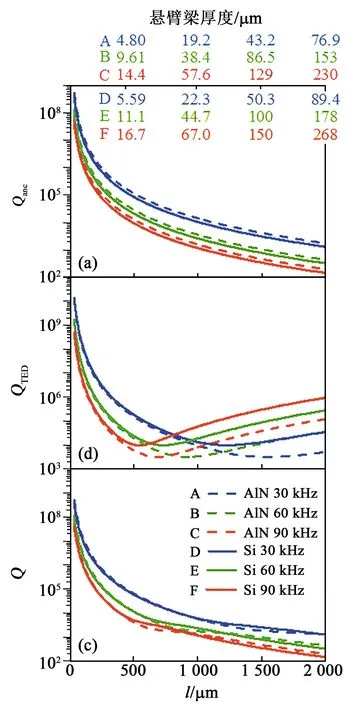
图2 恒定频率下悬臂梁谐振器品质因数随其长度变化情况

谐振器的热弹性阻尼损耗是指振动过程中因不均匀的弹性形变产生了温度梯度,导致局部热传递,从而引起不可逆的能量损失的现象。这种损耗所决定的QTED[23]为

(5)

式中:ρb和Cp分别为悬臂梁材料在常压下的密度和热容;αT为材料的线性热膨胀系数;T为工作温度;f0为悬臂梁的谐振频率;F0=πκ/2ρbCpt2为悬臂梁的热弛豫频率,其中κ为材料的热导率,将式(1)代入式(5),并以悬臂梁的长度为变量,当谐振频率保持不变时,悬臂梁的长度与谐振器的等效热弹性阻尼损耗品质因数(QTED)之间的关系如图2(b)所示。由图可见,对于固定频率的悬臂梁谐振器,其QTED随着悬臂梁厚度、长度的增加呈现先下降后上升的趋势,且频率越低,其转折点对应的梁长度越大,这说明硅基和氮化铝基悬臂梁谐振器的小型化有利于提高其QTED。此外,当悬臂梁长度小于500 μm时,对于不同频率的悬臂梁而言,氮化铝基的悬臂梁谐振器的QTED与硅基悬臂梁的QTED相当。

利用式(2)得到基于Qanc和QTED的谐振器总Q值,其结果如图2(c)所示。由图可见,固定频率的悬臂梁谐振器,其总Q值随长度增加而单调下降。通过分析Qanc和QTED的数量级可知,在梁长度较小时,二者量级相当,均会显著影响总Q值;在长度较大时,锚点损耗逐渐开始占主导地位,总Q值的趋势与Qanc一致。同时,在悬臂梁长度较低时,氮化铝基悬臂梁谐振器和硅基悬臂梁谐振器的总Q值相当,但使用氮化铝作为谐振器主体能有效减小谐振器厚度,也更符合氮化铝薄膜的加工制造特性。

由上述理论分析可知,通过选择合适的梁长度和厚度,可以实现相同频率下与硅基悬臂梁性能相当的氮化铝基悬臂梁谐振器。综合考虑悬臂梁谐振器的性能及加工难度,本文选定的基础器件设计尺寸参数为WC=50 mm,LC=300 mm,WE=44 mm,LE=298 mm,谐振器支撑层厚度(TS)、压电层厚度(TP)和电极层厚度(TE)分别为2.5 mm,1.0 mm,0.15 mm。

本文设计了不同的顶电极尺寸,用于研究电极设计对谐振器性能的影响。表2为电极设计参数变化范围。在悬臂梁谐振器的加工及测试中,每次仅会变更一组设计参数,剩余的设计参数与上述一致。顶电极长度和宽度的变化分别反映了谐振器在长度和宽度方向的电极覆盖率的变化。

表2 悬臂梁谐振器变量列表

2 谐振器加工及测试结果分析

2.1 谐振器加工

图3为悬臂梁谐振器的加工流程示意图。由图3(a)可见,首先是底部空腔刻蚀及牺牲材料的填充,该步骤中所用的牺牲材料为磷硅酸盐玻璃(PSG);图3(b)是支撑层AlN和底电极Mo的沉积及底电极Mo的图形化,支撑层和底电极的厚度分别为2.5 μm和0.15 μm;图3(c)是厚度为1 μm的压电层及厚度为0.15 μm的顶电极沉积;图3(d)是顶电极的图形化;图3(e)是测试电极图形的刻蚀;图3(f)是压电层和支撑层AlN的刻蚀;图3(g)是测试电极金的沉积和图形化,该步骤采用lift-off工艺,顶电极和底电极均被连接至位于底电极层的测试电极,金通过图3(e)所刻蚀的图形同时覆盖顶电极和测试电极以实现顶电极的电连接,底电极在步骤(b)的图形化阶段直接连接,在该侧视图中并未示出;图3(h)是悬臂梁谐振器的释放,该步骤使用氢氟酸溶液将牺牲材料去除干净。完成加工的悬臂梁谐振器在光学显微镜和扫描电子显微镜(SEM)下的表征结果如图4所示,图中同一空腔中的两悬臂梁谐振器相距足够远,保证了其性能不会相互影响。

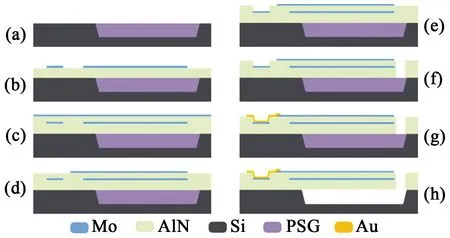
图3 悬臂梁谐振器的加工流程示意图

图4 悬臂梁谐振器的光学显微镜及SEM照片

2.2 谐振器测试及结果分析

本文主要研究在真空条件下悬臂梁谐振器性能及真空度对谐振器性能的影响。使用真空探针台和安捷伦E4990A型号阻抗分析仪对谐振器进行单端口测试,测试连接原理图如图5所示。真空探针台与真空泵、分子泵相连,可实现105～10-2Pa的真空度变化。在对悬臂梁谐振器的真空性能进行测试时,10-2Pa的真空度极大程度地减小了空气阻尼损耗对悬臂梁谐振器性能的影响,故空气阻尼损耗可忽略不计。

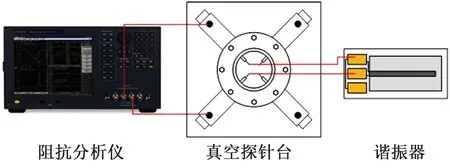
图5 悬臂梁谐振器测试连接原理图

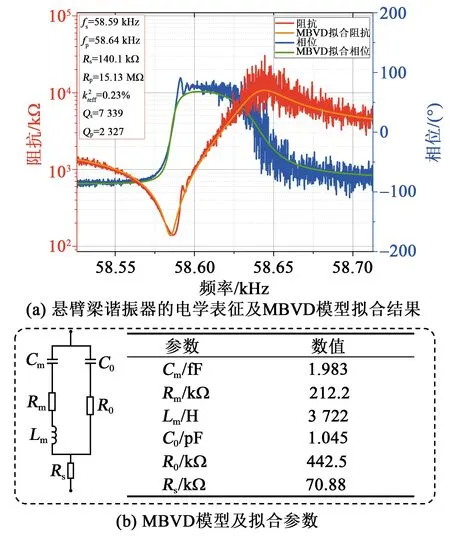
图6 悬臂梁谐振器基础器件的电学表征及MBVD模型拟合结果

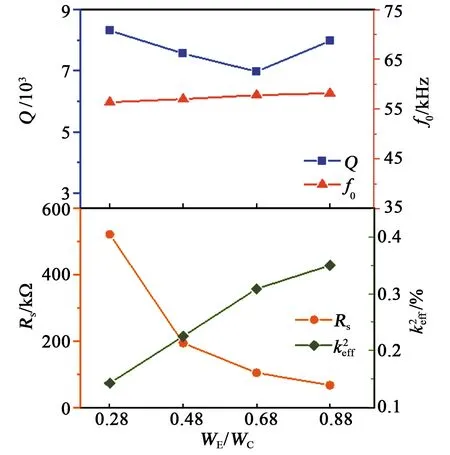
图7 顶电极宽度方向覆盖率对谐振器关键性能参数的影响

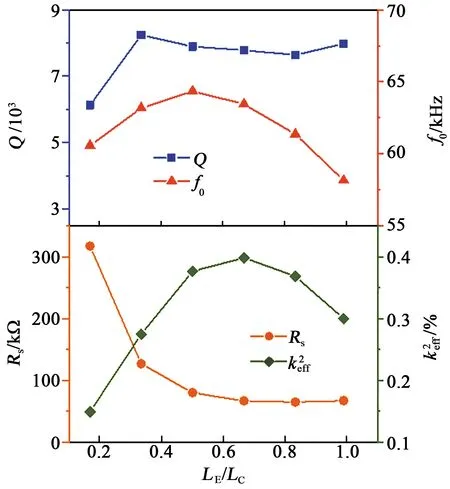
图8 顶电极长度方向覆盖率对谐振器关键性能参数的影响

在真空测试研究的基础上,本文对谐振器Q值受真空度变化的影响进行了研究,以确定谐振器可正常工作的真空度范围。图9展示了图6所使用的谐振器的性能随真空度变化的测试结果。由图可见,面外弯曲振动模式的悬臂梁谐振器受真空度变化影响显著,其Q值随压强的升高而迅速降低,在压强为230 Pa时基本无谐振特性。因此,在面外弯曲振动模态应用中必须采用较高真空度的封装才能保证其优良的Q值特性。

2.3 与现有研究成果对比

表3是本文所研究的悬臂梁谐振器与现有研究成果的对比,其中悬臂梁谐振器的测试条件均为真空。由表可见,由于PZT材料的高介电损耗,使用PZT作为压电材料的悬臂梁谐振器的品质因数普遍较低,而使用AlN作为压电材料将提高品质因数。与硅基悬臂谐振器相比,本文的AlN基悬臂谐振器具有更高的品质因数。

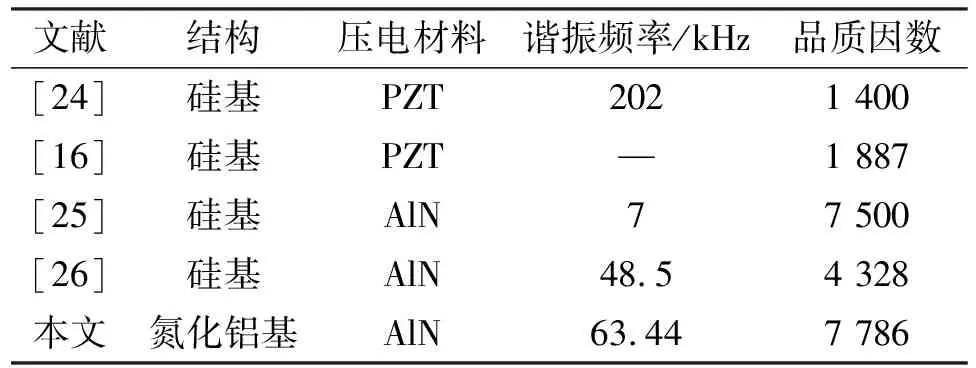
表3 现有研究与本文中悬臂梁谐振器真空条件下测试结果对比

3 结束语

本文提出了一种新型的面外弯曲振动模式压电驱动氮化铝基悬臂梁谐振器层叠结构,并对该结构的谐振器进行了设计、加工及测试分析。相比于传统压电驱动硅基悬臂梁谐振器,该结构能够简化加工流程,易与CMOS集成加工,且具有与硅基谐振器相当的品质因数。本文从理论和实验两方面研究了固定谐振频率下品质因数与器件尺寸的关系,以及谐振器的顶电极在宽度、长度方向的电极覆盖率对其性能的影响,并给出了最优设计参数范围。当悬臂梁谐振器的电极宽度占比为1,长度占比为0.50～0.83时,其表现出较高的品质因数及较低的运动阻抗,其中在电极长度占比为2/3时性能最佳。未来该新型悬臂梁谐振器有望集成到真空封装的谐振式压力传感器、加速度计、陀螺仪等传感器中,从而实现新型高性能谐振式MEMS传感器。