基于反对称模态驱动的MEMS加速度计灵敏度优化方法

刘 晨,武焕臣,洪逸飞,王发光,李 磊

(山东理工大学 交通与车辆工程学院,山东 淄博 255049)

0 引言

微机电系统(MEMS)传感器具有体积小、响应速度快、品质因数高、成本低和可集成的优势,被广泛应用于机械、汽车导航、消费电子等领域[1-4]。微机械谐振式传感器通过测量敏感元件谐振频率的偏移来反映被测物理量,具有稳定性好的优势。MEMS传感器作为一个重要的研究方向,逐渐被开发应用于加速度检测,质量检测,滤波,压力检测等[5-8]。

MEMS加速度传感器按照敏感机理的不同可分为谐振式、压阻式、电容式和隧道电流式。电容式加速度传感器是由质量块的运动位移导致检测电容发生变化,进而实现检测加速度的一种方式,但小输入范围和非线性限制了其应用。与微加速度电容式传感器相反,谐振式加速度传感器将加速度通过弹性梁支撑的质量块转化为惯性力,引起谐振元件谐振频率、谐振振幅或相位发生变化,通过检测这些变化来实现检测加速度的大小[9]。此外,谐振梁工作时受到轴向载荷,由此可获得大输入和宽动态范围[10]。目前,谐振式加速度传感器在已报道的微加速度传感器中具有最高精度。

2009年,Claudia Comi等[11]设计了一种高灵敏度的谐振式加速度计,它由2个单谐振梁、质量块、支撑梁、驱动及检测极板组成。实验测量了谐振器随加速度的频率变化,灵敏度为149 Hz/g。以频移作为输出的MEMS加速度计可以通过缩小尺寸来提高其灵敏度,但是随着尺寸的缩小,谐振器信号易受到外界干扰的影响。在不缩小尺寸的情况下,许多学者通过激发高阶模态来提升谐振器工作的灵敏度。2017年,Gao等[12]制作了一个压电质量传感器,通过实验测试发现,相较于一阶检测灵敏度,四阶模态检测灵敏度得到大幅提升;此外,谐振梁结构简单,也可用于其他物理量的测量。2019年,Li等[13]研究了静电激励双端固支梁的反对称响应进行质量检测应用,引入数值研究验证了质量检测方法的有效性。

在不减小谐振元件尺寸的前提下,通过驱动高阶模态可提高加速度检测灵敏度。由于二阶模态为反对称模态,一般难以被激发,为了更易驱动和检测反对称模态,本文设计了分布式电极来进行反对称模态的驱动和检测。同时设计了质量块以及具有小刚度的折叠梁作为加速度惯性元件,其制造工艺简单,幅值噪声低。为了减小空气阻尼的影响,在气压低于5 Pa的真空腔内对谐振式加速度计进行了实验。

1 加速度计结构尺寸和加工流程

单自由度的谐振式加速度计如图1所示。该结构由弹性梁支撑的质量块和谐振梁构成,将其用于加速度的检测。各项尺寸参数如表1所示。

表1 加速度计尺寸参数和物理特性

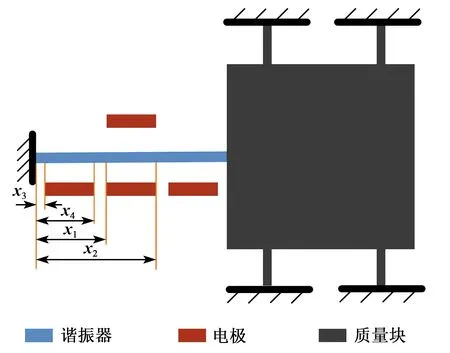
图1 加速度计结构示意图

本文设计的谐振式微加速度传感器采用商业SOI MEMS铸造工艺[14]。采用4英寸(1 in=2.54 cm)(100)P型双面抛光晶圆制作,器件层厚25 μm,绝缘层厚2 μm,基底层厚350 μm。加工工艺如图2(a)所示,其中①为基底层光刻胶沉积和图形化;②为ICP刻蚀基底层,刻蚀深度350 μm至埋氧层;③为BOE漂除埋氧层和正面光刻胶沉积和图形化,埋氧层厚度2 μm;④为器件层电极图形化;⑤为器件层结构光刻图形化和导气槽陪片粘贴;⑥采用ICP刻蚀器件层,刻蚀深度为25 μm,去除器件层图形光刻胶和移除导气槽陪片。最后采用激光划片得到单个器件结构,谐振器封装在DIP24常压陶瓷管壳中,以便后续实验对谐振器结构进行性能测试。封装和结构图如图2(b)所示。

图2 SOI加工流程、封装实物图

2 动力学模型分析

图3中一阶模态为弯曲模态,二阶模态为反对称模态。为了有效驱动一阶、二阶模态,采用分布式电极进行驱动。一阶模态采用中间电极进行驱动,二阶模态采用左侧电极驱动。采用不同的驱动方式可以激发不同模态。

图3 驱动形式及振型图

加速度计简化模型如图1所示,考虑非线性,直梁在静电激励下的横向运动微分方程[14]为

(1)

边界条件为

(2)

引入无量纲变量:

(3)

将式(2)、(3)带入式(1),得到无量纲方程为

(4)

其中

(5)

(6)

(7)

(8)

驱动电压下微梁挠度w(x,t)由直流电压的静态分量wd(x)和交流电压wa(x,t)的动态分量组成,即

w(x,t)=wd(x)+wa(x,t)

(9)

忽略式(4)中对时间的导数,交流驱动项的静挠度公式为

[U(xi)-U(xj)]

(10)

静位移对谐振器的固有频率有着重要影响,当轴向力为0时,计算中间电极驱动时的吸合电压。由图4可知,吸合电压约为167 V。

图4 静位移曲线

将式(9)带入式(4),再带入式(10)消除平衡位置得到前二阶公式为

(11)

由于Vd≫Va,得到

式(11)的解可表示为

(12)

式中φi(x)为第i个线性无阻尼阵型,特征值方程为

(13)

将式(13)带入式(10),得到

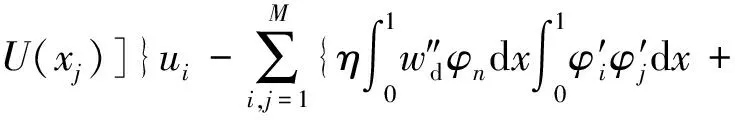
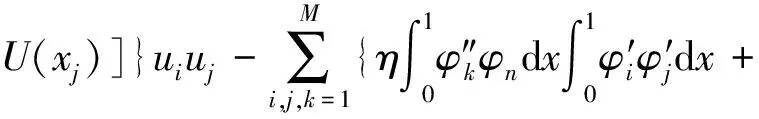
uiujuk=fncosΩt[U(x1)-U(x2)]

(14)

其中

(15)

通过式(14)得到频率的表达式为

(16)

3 实验方法及数据处理

测量系统包括直流稳压电源、真空腔、锁相放大器、跨阻放大器(OPA657)和PCB电路板等其余辅助设备。采用静电驱动、电容检测的方式开环检测了不同加速度时谐振频率的变化。电容式检测作为常用的一种检测方法,通过检测电容极板的电荷变化量来感知谐振梁的振幅变化,具有低功耗和检测精度高的优势。

图5给出了实验中谐振器开环测量电路及设备图。图中,中间电极2、3用于第一模态的驱动和检测,两侧电极1、4用于第二模态的驱动和检测。谐振器接地,交流电压Vac和直流偏置电压Vdc加载在平行驱动极板上,用于驱动谐振器。检测极板上通直流偏置电压Vd,用以产生运动电流,为了降低检测直流偏置电压对谐振梁的影响,这里Vd尽可能远小于Vdc。跨阻放大器用于将谐振器产生的电流信号im转换为电压信号vi,并放大输出信号。锁相放大器(LIA,Zurich Instruments MFLI)输出正弦激励信号,同时接受谐振器振动产生的振幅和相位信号来执行频率扫描,在显示器上即可读出谐振器的振幅、相位响应信息。实验过程采用重力法对谐振器加速度在-g～g内进行开环加速度灵敏度测试。

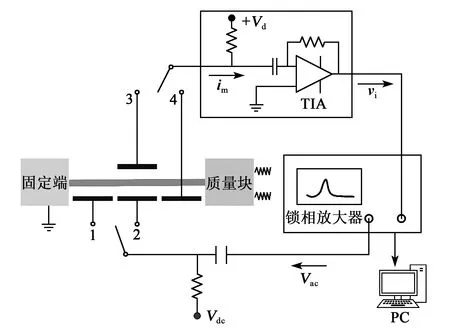
图5 实验测试原理图

MEMS接口电路中存在寄生馈通信号,馈通信号会使谐振器的实际振幅和相位发生偏转。如图6(a)所示,实验测量了直流偏置电压为7 V、交流电压为1 mV时,谐振器一阶补偿后带有馈通信号的振幅信号和馈通信号(关闭Vdc)。用matlab程序计算消除馈通信号后,可得谐振器的实际振幅曲线。

图6 测试信号和线性响应曲线

根据图6(b)中谐振梁的一阶、二阶线性频率响应曲线来确定其固有频率。谐振梁的一阶频率ω1为151.153 kHz,二阶频率ω2为406.167 kHz。在较小的激励下,利用半功率带宽法,根据图6(b) 线性响应曲线计算出谐振梁的品质因数。一阶的品质因数(Q)为14 152,二阶的品质因数(Q)为45 129。

图7 加速度为-g～g时谐振器一阶振幅响应曲线

图8为谐振器在Vdc=7 V,Vac=7 mV时的二阶振动幅频曲线。由图可见,谐振梁在二阶模态时,加速度在0～g内变化时,灵敏度为149.3 Hz/g;在-g～0内变化时,灵敏度为131.4 Hz/g。二阶检测灵敏度相对于一阶检测灵敏度有较大提升。其中正向检测灵敏度相较于一阶提升了49%,负向检测灵敏度提升了89%,实验证明高阶模态检测可以提高灵敏度。

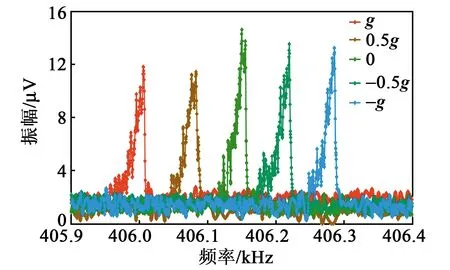
图8 加速度为-g～g时谐振器二阶振幅响应曲线

实验过程中,驱动交流电压Vac保持不变,改变直流偏置电压的值,探究了直流偏置电压对一阶加速度灵敏度的影响。

如图9所示,检测范围在-g～g,驱动电压为3 V、4 V和5 V时,加速度和频率成良好的线性关系。当电压为3 V时,加速度在-g～0时,灵敏度为72.8 Hz/g;加速度在0～g时,灵敏度为95 Hz/g。电压为4 V时,加速度在-g～0时,灵敏度为71.5 Hz/g;加速在0～g时,灵敏度为98.2 Hz/g。电压为5 V时,加速度在-g～0时,灵敏度为69.5 Hz/g;加速度在0～g时,灵敏度为100.1 Hz/g。驱动直流偏置电压为6 V时,在加速度为0.7g线性曲线发生了偏折;驱动直流偏置电压为7 V时,在加速度0.5g线性曲线发生偏折,此时加速度灵敏度提高,但是检测范围减小。这是因为施加直流电压过大,造成微梁静态弯曲,且谐振梁一阶为弯曲模态,受影响较大,导致灵敏度增大的同时测量范围缩小。

图9 不同电压下一阶加速度折线图

施加直流偏置电压引起的结构弯曲,可以通过测量谐振梁固有频率的改变来反映挠度。如图10所示,电压和谐振梁的固有频率成非线性关系,随着电压的升高,谐振梁的频率下降加快。

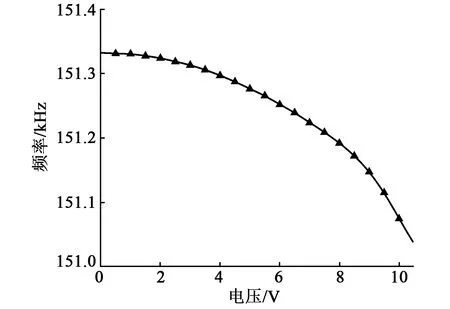
图10 电压对固有频率的影响

图11为直流偏置电压对二阶检测灵敏度的影响。由图可见,在二阶驱动电压下,直流偏置电压在4～8 V调节时,加速度和频率成良好的线性关系。因为二阶模态为反对称模态,谐振梁发生静态弯曲时对反对称模态的影响较小,实验结果证明了二阶反对称模态的检测稳定性优于一阶弯曲模态。

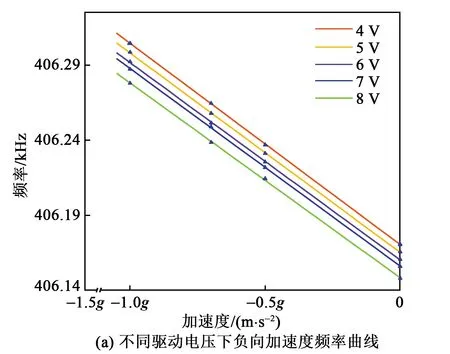
图11 不同电压下二阶加速度折线图

图12为加速度灵敏度和直流偏置电压的关系。由图12(a)可见,随着直流电压的升高,负向检测灵敏度不断降低,这说明电压增大的同时降低了负向检测灵敏度。由图12(b)可见,随着直流偏置电压的不断升高,正向加速度检测灵敏度不断升高,电压的升高有利于提高正向加速度检测灵敏度。

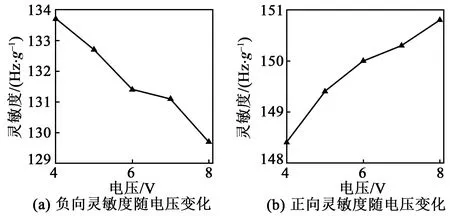
图12 二阶灵敏度随电压变化

幅值噪声也是衡量谐振器的一个重要指标。图13为关闭驱动电极直流偏置电压,仅施加交流驱动电压时,采集谐振器振幅信号,利用标准差计算谐振器的幅值噪声值为1.713 6×10-6。

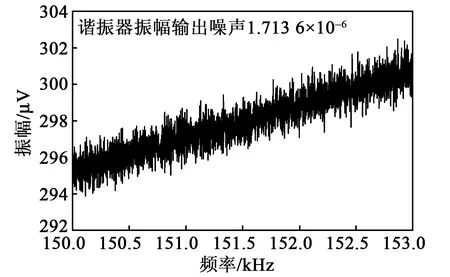
图13 谐振器的幅值噪声

微机械谐振器非线性的主要来源有几何非线性(硬化非线性)和静电非线性(软化非线性)。当几何非线性主导时,谐振器会产生刚度硬化现象,利用可调的静电非线性可以抵消几何非线性。实验测试结果如图14所示,直流偏置电压Vdc为10 V时,几何非线性占主导,此时产生刚度硬化现象;当Vdc为23 V时,此时几何非线性和静电非线性相互抵消,实验结果显示为线性振动。

图14 非线性相互抵消

4 结束语

本文设计制造了分布式电极驱动及检测MEMS加速度计,驱动了谐振梁的反对称模态。建立了谐振梁在不同驱动条件下的一阶、二阶加速度传感器动力学理论模型。首先通过实验测量了谐振梁前二阶模态的品质因数,二阶模态比一阶模态具有更高的品质因数。采用重力法测量了不同加速度条件下谐振梁的频率变化,对比谐振梁的一阶、二阶加速度检测灵敏度,发现二阶正向检测灵敏度比一阶提高了49%,负向检测灵敏度比一阶提高了89%。实验探究了不同电压下加速度对一阶的频率变化,并进行了加速度频率曲线拟合。对于一阶模态,当驱动电压不断增大时,其检测灵敏度提高检测范围在减小。实验发现加速度和二阶频率成良好的线性关系,其原因是反对称模态受谐振梁弯曲影响较小。二阶正向灵敏度随着电压升高而提高,而负向灵敏度会降低。结果表明,二阶反对称模态比一阶弯曲模态具有更高的灵敏度和品质因数,电压稳定性优于一阶。最后实验探究了几何非线性和静电非线性现象两者的相互作用,逐步增大直流电压直至抵消几何非线性。