基于snake算法的声呐图像轮廓提取方法

杨卫东,叶长彬,陈正林,董加和,肖 强

(中国电子科技集团公司第二十六研究所,重庆 400060)

0 引言

21世纪初,联合国缔约国文件指出:“21世纪是海洋世纪”,如何成为海洋强国必将成为各国发展的重要目标。随着各国对海洋重视程度日益加深,为了进一步开发和利用海洋资源,人们对海洋技术的发展也愈加重视。成像声呐作为水下声呐设备的一种探测结果,伴随着海底环境的日益复杂,测扫等成像设备往往无法给出明确的结果。此时,成像声呐水下目标检测技术显得尤为重要。传统的成像处理方法在去除背景时,通常采用背景相减法,该方法直接应用原始图像与对应的背景图像相减,从而实现图像的去背景效果。研究发现,声呐设备采集到的成像图片[1]均具有一定的随机性,采用背景相减法所获得的前景图,往往会出现目标的随机缺失。其次在进行目标边缘提取时,传统边缘检测方法[2]有两种:一种是以一阶导作为基础算子,通过图像梯度值变化实现边缘检测,常见算法有Roberts、Sobel、Prewitt等;另一种是通过二阶导为基础,以二阶导数中零交叉进行边缘检测,常见算法有Laplacian、LOG、canny。虽然以上方法也可实现对目标轮廓的提取,但该类方法实现需要声呐图像较强的前景和背景识别度,且所得检测结果不具备连续性。

为解决上述问题,本文充分利用成像声呐背景的高斯特性,通过高斯模型对图像中各个点元素进行统计,构建高斯背景模型[3-4];再通过高斯模型对图中点元素进行判定,对图像中前景和背景进行区分。为进一步保证高斯背景模型的时效性,对背景信息采用迭代更新,当判定该点为背景时,将该点纳入高斯模型进行统计,反之判定为前景则跳过。然后结合梯度矢量流(GVF)改进的snake模型对图片中前景目标进行轮廓提取,得到连续的目标轮廓曲线。最后利用计算机仿真对本文方法与传统方法进行对比分析,验证了所提方法的有效性。

1 声呐图像前景提取算法

传统声呐图像前景提取方法,通过简单的背景相减法对图像前景目标进行提取。背景相减法是声呐图像通过与之匹配的声呐背景图像进行相减,被减去背景后的声呐图像便作为声呐前景图像。其表达式为

P(x,y)=I(x,y)-B(x,y)

(1)

式中:(x,y)代表图像在笛卡尔坐标系下横坐标x和纵坐标y位置;I(x,y)为声呐原始图像在(x,y)位置处像素值;B(x,y)为声呐背景图像在(x,y)处像素值;P(x,y)经过传统背景相减法后取得的声呐前景图像在(x,y)处像素值。

本文采用基于高斯模型算法对声呐图像进行前景提取。通常水声成像设备在进行水下图像采集时会受到噪声的干扰。当面对静态图像进行采集时,受噪声影响所采集到的声呐图像像素值并非恒定不变,往往在原始图像像素值的基础上加入一个随机值随着时间变化,通常声呐图像中背景可当作静态目标。基于上述特征,本文引入高斯模型对声呐图像所采集的背景信息进行高斯建模,通过高斯模型对一段时间内图像中所有像素进行统计,区分前景和背景。

假设声呐图像中像素点都相互独立,且均服从一维的正态分布,首先对一段时间内多帧声呐图像进行处理,计算出声呐图像中每个像素点的灰度值方差和均值,计算公式如下:

(2)

结合式(2)中统计信息,得到高斯模型:

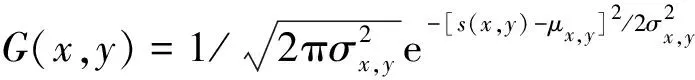
(3)

根据式(3),通过多次运算统计可找到一个区分前景和背景的阈值th,将(x,y)处像素点分别代入高斯模型中,输出概况密度小于经验阈值th时,定义该点为背景点,反之则定义为前景点。即

(4)

根据式(4)的结果,当判定该点属于前景时,该点背景模型参数不变;当判定该点属于背景点时,则对该点模型进行迭代更新,以保证高斯模型的实时有效性,更新公式为

Bt(x,y)=αIt(x,y)+(1-α)Bt-1(x,y)

(5)

式中:α为更新系数;Bt(x,y)为当前(x,y)处的背景信息;Bt-1(x,y)为前一帧(x,y)处的背景信息;It(x,y)为当前(x,y)处原始声呐图像。

由上述推导可见,采用高斯法对声呐图像进行前景提取时,每个图像点处像素点的概率密度和阈值存在一定关系。为了提高判定准确率,选择合适的阈值对声呐图像前景、背景的判定至关重要。经验阈值计算公式为

th=Ωσx,y

(6)

由式(6)可计算(x,y)处前景、背景判定经验阈值,其中Ω为经验系数,该系数通常选取2.5～3之间。

2 前景目标轮廓提取方法

与传统边缘检测算法不同,本文采用改进的snake模型方法实现对声呐图像前景目标的轮廓提取。该方法结合B样条曲线[5]自身所具有的内力和声呐图像数据带来的外部约束力的相互作用下移动变形的轮廓曲线,再根据轮廓当前位置以及形状决定空间变化方式,最终逼近声呐图像前景目标轮廓。

首先给出B样条曲线表达式为

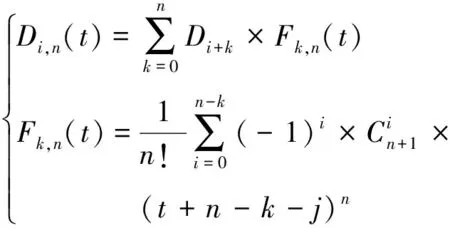
(7)

式中:0≤t≤1;i=0,1,2,…;通过对B样条曲线进行分段定义,给定m+n+1个定点Di,n(t),即可定义m+1段n次参数的曲线;Fk,n(t)为n次B样条曲线的基础函数。

通过连接曲线段所组成的线条为n次snake曲线,依次用直线连接Di,n(t)多点组成多边形折现即为B样条曲线在其i段的snake特征[6-7],如图1给出定点为5情况下拟合三阶B样条曲线。

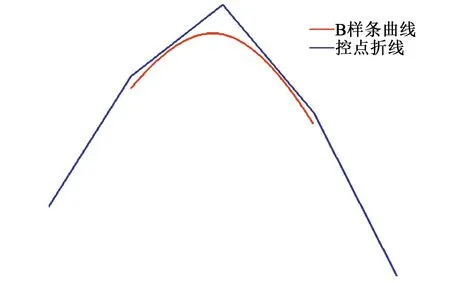
图1 5点三阶B样条曲线

假设取弧长为h∈[0,1],活动的轮廓曲线为d(h)=[x(h),y(h)],则其能量函数可写为

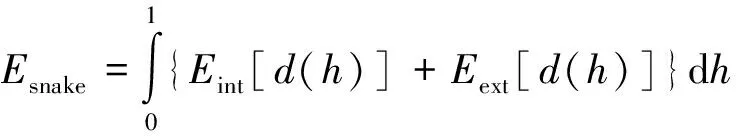
(8)

式中Eint和Eext分别表示内部能量和外部能量。

内部能量可写为

(9)

式中:α和β分别为控制参数曲线弹性和刚性的参数;d′和d″分别为d的一阶导数和二阶导数。

外部力是由声呐图像与其外部约束力所产生,其能量组成为

Eext(d(s))=γ(h)Eimage(d(h))+

Econstrain(d(h))

(10)

式中:Econstrain表示snake曲线的外部约束力所带来的能量;Eimage表示图像能量,反应声呐图像的本质特征,可保证snake曲线逼近期望目标发生形变。通常可采用以下函数进行表达:

(11)

式中:Gσ为标准差σ的二维高斯函数;∇为梯度算子。

根据式(8),对snake曲线d(h)沿着弧长以N个采样点进行抽样,每个采样点为di,i=1,2,…,N,得到离散能量函数表达式为

(12)

外部力和内部力分别表示为

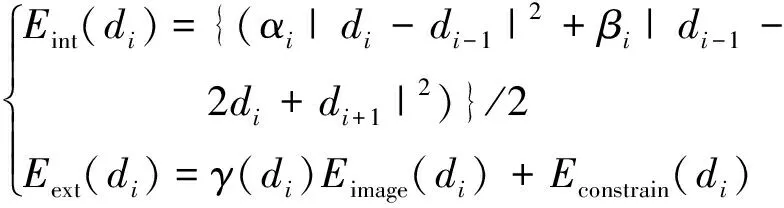
(13)

snake曲线是根据能量最小原则来实现对前景目标轮廓的逼近。为了保证总能量Esnake趋于最小,通过欧拉方程可以得到其一阶偏微分方程,以此来得到能量平衡方程为。

αd′(h)-βd″(h)-∇Eext=0

(14)

通过能量方程得到力的平衡方程为

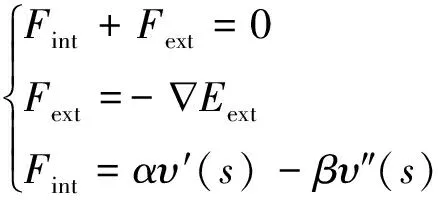
(15)

式中:Fext为外部力可使轮廓逐渐向真是轮廓逼近;Fint为内部力可控制曲线特征。

因此,为实现snake模型完成声呐图像目标轮廓提取,不仅需要内部力驱使初始线条的特征逐渐逼近真实轮廓曲线的过程,而且需要外部力使活动轮廓逼近真实轮廓,当力达到平衡时,即外部力和内部力相加为0,此时表示snake模型曲线已停留在真实轮廓上面。

3 基于GVF改进的snake模型[8-10]

梯度矢量流(GVF)首先是在真实轮廓边缘建立一个扩散的梯度矢量场,动态轮廓通过该外部力的作用,可更快地逼近声呐图像前景目标轮廓。

设GVF矢量场d(x,y)=[φ(x,y),φ(x,y)],首先在声呐图像中获取一个初始轮廓f(x,y),由此可得边界矢量梯度值∇f是初始轮廓趋于较大的值,而均匀区域∇f趋近于0,且该矢量梯度方向是朝向内轮廓。以此为条件求解能量函数最小化为

|∇f|2×|d-∇f|2dxdy

(16)

其中

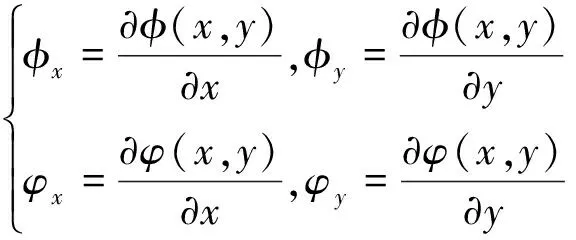
(17)

规则化参数μ可根据实际声呐图像中的噪声情况进行取值,噪声大,则可增加μ值,反之则减小。在处理声呐图像均匀区域时,∇f较小,此时将矢量场偏导平方和作为当前能量,产生一个变化较缓的矢量场。

由式(14)可见,活动轮廓向真实轮廓逼近,实质上是寻求能量函数最小值的过程,当内部力和外部力为0时可达到平衡。因此,利用变分原理,通过对式(14)进行求解可得梯度矢量场为

μ×∇2d-(d-∇f)×|∇f|2=0

(18)

式中∇2为拉普拉斯算子。通过fx=∂f(x,y)/∂x和fy=∂f(x,y)/∂y可得:

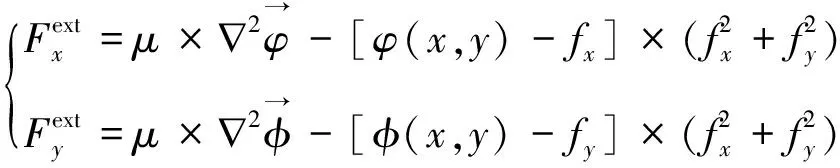
(19)

初始轮廓曲线可分成多个线段实现,表达式为

{Di(t)|i=0,1,2,3,…,n-1,t∈[0,1]}

(20)

曲线段通过控制点列(V1,V2,V3,…,Vq)来达到曲线形状,因此可得m次等间距分割B样条曲线公式为

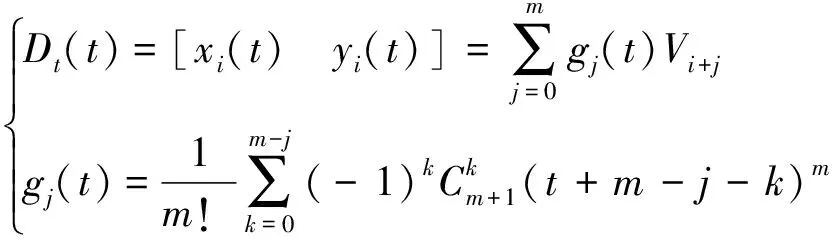
(21)

式中:i=0,1,2,…,n-k;j=0,1,2,…,m;控制点Vi+j的基函数为gj(t)。本文采用三阶B样条曲线实现曲线对真实轮廓逼近,得到活动轮廓初始位置在第i段的三阶B样条曲线矩阵函数表达式为

(22)

由式(22)可见,三阶B样条曲线的每段都由4个控制点来实现,改变其中一点仅影响相邻两段曲线,增加一个点便可增加一条新的曲线段,在不影响原曲线段的同时,新增加的曲线段还与原曲线段具有连续性。

在给定n个离散点作为初始控制点时,其B样条曲线上的节点可表示为

(23)

对式(23)进行变化后可得系数矩阵Cj:

(24)

式中(gj(t))-1是gj(t)卷积的逆变换。通常所提取的目标轮廓为一个封闭曲线,故对封闭曲线而言,控制点必须满足首尾相连,即

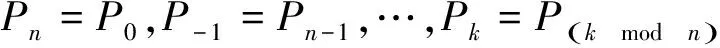
(25)

Fint=αd′(h)-βd″(h)

(26)

本文方法与传统snake轮廓曲线相比,传统方法是在曲线上的像素点进行迭代更新以实现逼近轮廓。假设每段曲线离散m个像素点,对于n段三阶B样条曲线构成的运动轮廓而言,其在逼近过程中经过的坐标点数为m×n个,所需时间复杂度为O(m×n)。本文基于GVF改进的方法,其三阶B样条曲线是由4个控制点完成,逼近过程中经过坐标点数为4×n,即时间复杂度为O(n)。通常情况下m≫4,通过GVF改进后的snake曲线节约了对声呐图像前景目标轮廓提取的时间。

4 算法仿真分析

仿真分析分别针对不同背景(固定干扰背景及动态噪声干扰背景)下,所选取声纳图像中目标个数分别为单目标及双目标情况下,进行声呐图像前景提取及目标轮廓提取的仿真分析。

4.1 前景提取试验

如图2和图3、4所示,分别给出两种不同环境下声呐图像。其中图2中存在固定干扰背景,图3、4中存在动态噪声干扰背景。分别对两种不同环境下的声呐图像进行前景提取。通过对比分析发现,传统的背景相减法,所取得结果前景图像连续性较低,原因在于当图像声纳中背景点与前景点重合时,前景所在位置像素值会被该点背景像素值减掉,从而导致前景目标不完整,存在部分缺失,如图5(a)和图6(a)所示。本文所采用的方法对前景目标的整体影响较小,且对背景去除较为彻底,如图5(b)、图6(b)和图7所示。

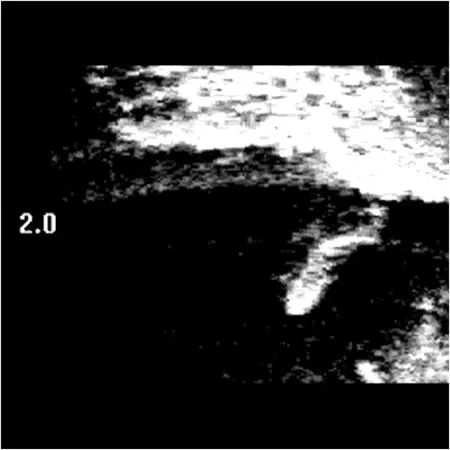
图2 原始声呐图像1

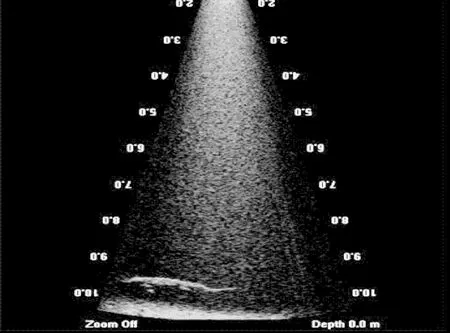
图3 原始声呐图像2

图4 原始声呐图像3

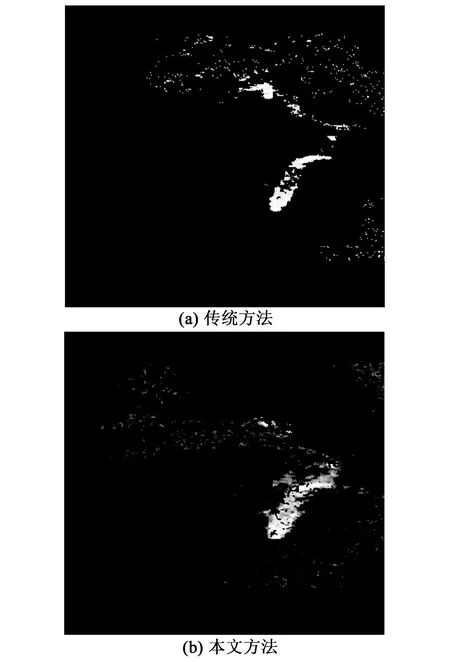
图5 去背景后声呐图像1

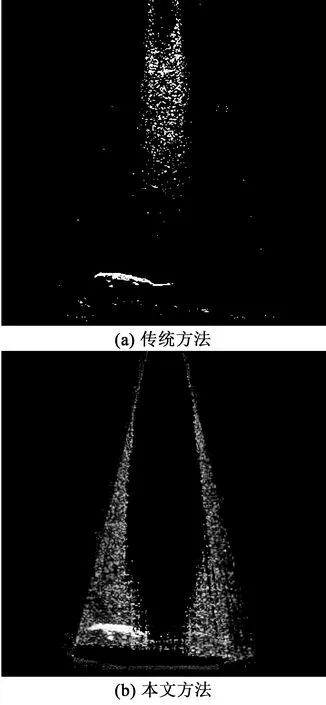
图6 去背景后声呐图像2

图7 去背景后声呐图像3

4.2 目标轮廓提取

图8和图9分别为同一段声纳探测结果中不同帧图像,图10为存在固定干扰的声纳图像单帧图像,图11为传统轮廓提取图像。对图8原始声呐图像经过传统Sobel边缘检测方法的结果如图12所示,图中可以看出传统方法虽然大致寻到了目标轮廓,但所提取的轮廓边缘存在不连续断点,在处理声纳图像背景复杂度较高的图像时,所检测到的边缘与实际目标轮廓误差较大,从而间接导致依据目标轮廓特征来判别目标类型出错。

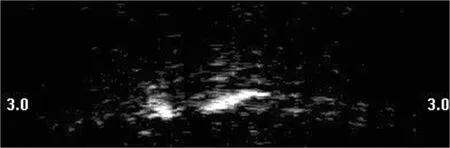
图8 原始声呐图像3

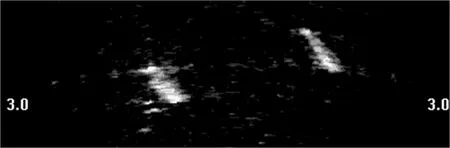
图9 原始声呐图像4

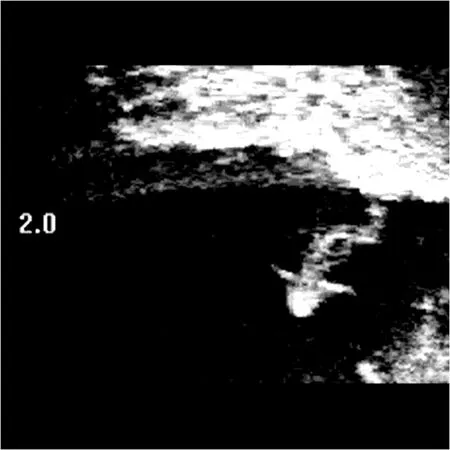
图10 原始声呐图像5

图11 传统轮廓提取图像3

图12 传统轮廓提取图像4

为提高目标前景的完整性,本文首先采用高斯法对声纳图像中前景和背景信息进行区别,从而活得完整的图像目标像素点集。其次采用基于GVF改进的snake目标轮廓提取方法,进一步成功获得目标完整的轮廓曲线。如图12和图13所示,图12中(a)和(b)分别为图9中双鱼目标轮廓提取结果,图13为图10中目标轮廓提取结果。

图13 传统轮廓提取图像5

采用传统Sobel算法所提取的目标轮廓结果与本文基于GVF改进的snake方法对比可看出,传统方法所取得结果连续性较差,且会造成目标缺失,而本文所采用的方法所得到的目标轮廓连续且精细化高。

5 结束语

本文针对声呐图像目标轮廓提取的问题,结合高斯模型算法和snake模型算法提出了一种基于snake算法的图像轮廓提取方法。在前景提取方面,该方法利用声呐图像中前景和背景的不同特性,构建了声呐图像背景中各个像素位置处像素值的高斯模型,以高斯概率密度对前景和背景进行判定区分,并在处理的同时对声呐图像进行迭代更新,保证了模型的实时有效性,最终实现目标前景像素集的识别。高斯法前景提取方法与传统背景相减法相比,高斯法具有更高的去背景能力以及保留更完整的前景目标。在目标轮廓提取方面,本文利用snake曲线自身特性,构建snake模型,再结合GVF对其进行改进,最终实现快速有效的目标轮廓提取。与传统目标轮廓提取算法相比,该方法所获得轮廓更接近真实目标,且保证了轮廓的连续性。