基于全期望公式的随机红包算法分析

张志刚, 刘秀芹, 陈 萱

(北京科技大学 数理学院,北京 100083)

0 引 言

随着移动互联网的崛起,微信的全球用户数已突破10亿大关,成为在中国普及率最高的通讯社交软件.微信红包是腾讯公司于2014年推出的一款应用,其发放形式共有两种:一种是普通等额红包,一对一或者一对多发送;另一种被称作“拼手气红包”,用户设定好总金额以及红包个数之后,可以生成不同金额的红包,在功能设计上遵循随机发放的原则.文献[1]基于随机红包金额的数值特征,构造红包金额的模拟算法,并对随机红包中的一些问题进行了分析.但此类相关的研究还较少,本文利用全期望公式相关知识,来对随机红包分配机理层层分析.有关全期望公式的应用有很多,如巴格达窃贼问题、复合泊松过程的期望、方差的计算等[2],然而这些应用与实际生活关系并不紧密,难以引起学生对事件背后原因的探索.文献[3]选择以新型冠状病毒为例,从全期望公式的角度对事件进行分析,极大地调动了学生的探索求知兴趣.本文选择对微信红包这一与生活息息相关的问题进行分析,引发同学们的求知欲,从而引导学生循序渐进的计算总结相关过程,让学生理解和掌握相关知识点,进一步加深印象,并能从实际中来,回到实际中去,达到“学以致用,以用促学”的目的[4-6].

1 全期望公式

随机变量的数学期望作为最基本的数字特征之一,反映了随机变量平均值的大小.在某些情形下,随机变量的期望很难直接计算,需要借助全期望公式进行:设X,Y是任意两个随机变量,则它们之间满足以下等式:

E(X)=E(E(X|Y)),

(1)

称(1)式为全期望公式,证明可以参见文献[2].

2 全期望公式在随机红包分布中的应用

随机红包问题中,设每份红包的金额服从零到剩余平均金额的两倍之间的均匀分布.用s表示红包总金额,n表示红包份数,Xi表示第i个领取者抽到的金额,将Xi视为连续型变量,则

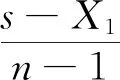
同理得

2.1 当红包个数小于4时随机红包金额的概率密度函数

由于红包金额服从均匀分布,因此,将对随机红包金额的概率密度函数进行推导,以进一步推导出红包金额的数学期望.

从而得到X1,X2的联合概率密度函数

(2)

将f(x1,x2)对x1进行积分,得到X2的概率密度函数

从而得到X1,X2,X3的联合概率密度函数

f(x1,x2,x3)=fX1(x1)fX2|X1(x2|x1)fX3|(X1,X2)(x3|(x1,x2))

由于知道x1,x2,x3的取值范围,根据截面,可以确定积分范围(图1),再通过对x1,x2进行二重积分,得到X3的概率密度函数.

图1 前三个人红包金额的取值空间示意图(n=4,s=1)

对X3的坐标,按照从高到低排列有

随后,只对上述一种情况进行分析,其余情况类似可得

由推导过程可知,随着红包个数的增加,红包金额的概率密度函数的计算复杂度会随之增加,在此不再进行后续的推导.

利用前文得到的密度函数,可计算随机变量Xi的期望

由此可知,依赖于红包金额的概率密度函数进行期望的计算,在随着红包个数增加时,也会由于密度函数计算的复杂性增加,而增加自身计算的复杂性,因此需要寻求一种更加简单的方式,来计算红包个数已知条件下每个随机红包金额的期望.

2.2 利用全期望公式求解随机红包金额的期望

类似地,可以得到

由此可知,当红包个数较多时,通过概率密度函数表达式计算期望非常复杂,而基于全期望公式的随机变量期望的计算简单很多,因此可以考虑采用全期望公式计算随机变量Xi的期望.

2.3 利用全期望公式求解随机红包金额的方差

(i) 计算X1的方差.

(ii) 计算X2的方差.

由全期望公式:

(iii) 计算X3的方差(n≥3).

先计算X1与X2的协方差Cov(X1,X2),

其中

E[(s-X1-X2)2]=D(s-X1-X2)+[E(s-X1-X2)]2

即DX3>DX2.

显然,在计算DX3时,用到了X1与X2的协方差Cov(X1,X2),求协方差的关键是计算E(X1X2).

(iv) 计算X4的方差(n≥4).

下面计算(X1,X2,X3)的协方差,

DX4=D(s-X1-X2-X3)=DX1+DX2+DX3+2Cov(X1,X2)+2Cov(X1,X3)+2Cov(X2,X3)

显然,在计算DX4时,用到了(X1,X2,X3)的协方差矩阵,关键是计算E(X1X2),E(X1X3),E(X2X3).

接下来计算(X1,X2,X3)与X4的协方差,

Cov(X3,X4)=Cov(X3,s-X1-X2-X3)

综上,已经推导出(X1,X2,X3,X4)的协方差矩阵.

(v) 下面给出计算Xk方差的步骤(任意k∈,n≥k).

E[(s-X1-…-Xk-1)2]=D(s-X1-…-Xk-1)+[E(s-X1-…-Xk-1)]2,

其中

为计算Cov(XiXj),先计算E(XiXj) (1≤i

按顺序依次计算以下矩阵上三角中的元素

由此,给出了计算Xk的方差的步骤.

3 实例分析

对于随机红包问题的分析,主要考虑从三个方面入手,一是对抢到的红包金额的均值而言,是先抢多还是后抢多;二是抢到红包金额的波动,是先抢大还是后抢大;三是通过计算不同位次处拿到手气最佳的概率,明确应该在何处抢红包最合适.而这三个问题,简要来说,就是对随机红包金额的期望、方差以及最值的概率这三个数字特征进行考察.

3.1 两个人抢红包

设红包的总金额为s,分给2个人,随机变量Xi表示第i个领取者抽到的金额,将Xi视为连续型变量,即X1～U(0,s),第一个人抢到红包之后,X2=s-X1.则有

可见,两个人抢到的红包期望和方差都是相等的,说明先抢后抢得到的红包金额均值以及金额波动没有区别.

3.2 三个人抢红包

计算第二个人红包金额的期望和方差,由X2|X1～U(0,s-X1)及全期望公式得到X2的期望

进一步计算(X1,X2,X3)的协方差矩阵

由此可知,三个人抢红包,先抢后抢获得的红包金额均值是相同的;但方差不同,即抢到的红包金额的波动性不同,方差越大,抢到的金额出现较大值和较小值的概率更高,对于进取型的人来说,适合采取此方法,但需要同时承担的风险也越大;方差越小,抢到的金额基本会贴近红包金额的均值,适用于保守型的人抢红包.

为了验证计算结果,利用Matlab软件进行计算机模拟演示.以总金额s=1,红包个数n=3为例,计算机模拟300次实验,模拟结果如图2、图3所示.

图2 随机红包的平均值模拟 图3 随机红包的方差模拟

图2中,横轴表示实验次数,纵轴表示每个人红包的平均值,三条曲线分别表示三个人的红包平均值曲线.由图2可见,随着模拟次数的增加,三个人红包的均值将基本稳定在1/3附近,与前面随机红包金额期望计算结果一致.图3是三人随机红包的方差模拟图,横轴表示实验次数;纵轴表示每个人红包值的方差;三条曲线分别表示三个人的红包金额方差曲线.由图3可见,随着模拟次数的增加,第一位抢红包的人的金额方差基本趋近1/27(≈0.037),而后面两位抢红包人的金额方差基本趋近4/81(≈0.049),这些计算机模拟结果与随机红包金额方差理论计算值一致.

接下来,将对三个红包的最值的概率进行推导,求得红包金额X1,X2,X3各取得最大、最小值时的概率.

由前文推导得到的X1与X2的联合概率密度函数(式(2))曲面如图4所示,图5为X1,X2,X3取得最大、最小值对应的平面区域:

图4 前两个红包金额联合概率密度函数曲面图

图5 求大、最小值概率的二重积分对应的积分区域示意图

(i)X1取得最大值的概率

p1=P{X1≥X2,X1≥X3}=P{X1≥X2,2X1+X2≥s}

(ii)X2取得最大值的概率

p2=P{X2≥X1,X2≥X3}=P{X2≥X1,X1+2X2≥s}

=0.3185.

(iii)X3取得最大值的概率

p3=P{X3≥X1,X3≥X2}

=P{s-X1-X2≥X1,s-X1-X2≥X2}

=0.3185.

(iv)X1取得最小值的概率

p4=P{X1≤X2,X1≤X3}=P{X1≤X2,X1≤s-X1-X2}

(v)X2取得最小值的概率

p5=P{X2≤X1,X2≤X3}=P{X2≤X1,X2≤s-X1-X2}=P{X2≤X1,X1+2X2≤s}

(vi)X3取得最小值的概率

由此可知,当只有3个人抢红包时,第一个人抢到手气最佳的概率最大,第二个和第三个人抢到手气最佳的概率是相等的;而第一个人抢到手气最差的概率最小,第二个和第三个人抢到手气最差的概率相等.

为了验证计算结果,利用Matlab软件进行计算机模拟.以总金额s=1,红包个数n=3为例,计算机模拟106次,模拟结果如图6(第一张图)所示,图中,横轴表示抢红包的位次,纵轴表示抢到手气最佳和最差红包的概率,由图可见,三个人抢红包时得到手气最佳、手气最差的概率值与前面的计算结果一致.

图6 人数从3到14时,不同位次抢得手气最佳和手气最差的概率变化图

由于对不同位次抢红包得到最大金额和最小金额的计算随着人数的增加而趋于复杂,因此利用模拟实验以进一步探索多人抢红包情况下,不同位次抢红包得到金额的最大值、最小值与综合收益的概率情况,模拟结果如图6、图7所示.

图7 人数从3到26变化时,不同位次的收益变化图

由图6可知,多人参与抢红包,人数小于9时,第一个抢红包的人得到手气最佳的概率最大,人数大于8时,手气最佳的概率随着位次的增加,先减少后增加,且最后两个人得到手气最佳的概率最大且相等.而不论人数多少,手气最差的概率随着位次的增加而增加,且最后两个人得到手气最差的概率一直为最大.

进一步,利用上面模拟产生的数据,对于不同位次的人抢红包的收益情况做了进一步分析,对一个给定的人数n(3≤n≤26),按照前面给出的概率分布产生第1到n个人的红包金额,将这n个人的红包金额从小到大排序,用第i个人(i=1,2,…,n)抢到的红包金额在数组中的次序除以1到n的和,作为他的收益值,上述步骤重复106次,然后计算第i个人的平均收益;参与抢红包的人数n取3到26变化的情形下,都计算第i个人的平均收益,并绘制收益折线图,由图7可见,当总人数从3到9时,位次靠前的人得到的红包金额更大,且随着位次的后移,金额随之减少,最后两个人得到的红包金额相等;当人数在10到12时,金额虽然随着位次的增加,出现了先减少后增加的变化,但整体上变化不大;当人数大于12时,可以发现金额随着位次的增加,出现了先减少后增加的变化,且最后两个人得到的金额最大且相等,而这一规律也与图6中所表示的手气最佳和手气最差的概率规律相吻合.

因此通过对红包金额的期望、方差以及相关事件发生的概率进行分析,可以更好地揭示随机抢红包的原理机制,引导学生理解掌握相关知识,达到学以致用,以用促学的目的.

4 结 论

有趣而又贴近生活的随机红包案例,通过全期望公式简洁地揭示了随机红包金额背后的分配原理,既能成功的抓住学生的注意力,调动学生的参与热情,激发学生的兴趣和求知欲,同时又有目标、有条理并逐步深入地帮助学生找到解决问题的方法,并通过Matlab模拟,加深学生对全期望公式的直观印象,有助于学生更好地学习和掌握内容.通过实际问题的解决,也让学生对全期望公式乃至概率论与数理统计有了更加深入的理解,对理论知识在实际问题中的运用有了深刻的认识,从而促进学生的学习兴趣,达到了“用以促学”,培养学生的创新精神和思维能力.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.