面向数据质量的隐私保护多分类LR方案
曹来成,吴文涛,冯 涛,郭 显
(兰州理工大学 计算机与通信学院,甘肃 兰州 730050)
1 引 言
随着计算机计算能力的发展,机器学习技术在推荐、认证、威胁分析等服务中被广泛应用于生成预测模型。虽然该技术在语音、图像、文本等领域中都取得了重要的突破,也使得很多问题有了新的解决办法,但是它需要收集大量的用户数据,因此其安全和隐私问题不容小觑,如何保护数据的隐私已经成为了一个重要问题[1]。
保护数据隐私的一种方法是在将数据上传到云中之前对数据进行加密。在现今流行的云计算服务中,服务器和云服务提供商在用户结束服务很长时间后依旧可以访问用户数据,但云计算不能侵犯用户的数据隐私,这个挑战可以通过使用同态加密方案[2]来解决,该方案允许在不解密的情况下对加密数据执行操作,而不会泄漏结果以外的任何信息,在密文域中进行计算,将计算后的结果解密就相当于在明文下直接计算。同态加密技术可以对机器学习进行隐私保护,利用加密数据训练机器学习模型,将结果返回给用户自行解密,达到保护用户敏感信息的目的。
AHARONI等[3]提出了一个基于同态加密的安全逻辑回归模型,但这种解决方案只能分析二分类问题,而现实生活中存在许多分类问题[4]。SINHA等[5]使用近似同态加密方案(Cheon-Kim-Kim-Song,CKKS),以位分片的形式应用量化和适当的数据打包,以减少噪声;然而随着迭代次数的增加,CKKS方案的参数也需要变大,这使得训练时间急剧增加。JANG等[6]引入扩展的CKKS方案MatHEAAN(Matrix HEAAN),以提供有效的矩阵表示和运算以及改进的噪声控制;但是随着样本数量的增加,可用操作的范围和网络的深度会受到限制。YAN等[7]提出了一种具有隐私保护特性的算法来解决多分类问题,将目标函数的梯度信息作为代理的隐私信息;但是该算法在训练期间没有考虑数据质量和数据稀疏问题。JIA等[8]结合可搜索加密和同态加密,使服务器可以通过盲查询陷门和索引执行密文数据搜索,使用搜索到的同态密文进行模型训练;但是在对于不同用户发送相同请求的冗余训练时,模型存储空间增大,耗时较长。FU等[9]提出了一种两方纵向联邦逻辑回归协议,该协议通过同态加密技术来保证特征数据和标签信息的安全,虽然可以保证模型无损,但是没有对非线性函数使用多项式近似计算,且没有考虑模型参数隐私。ZHAO等[10]构建了一个逻辑回归模型,将数据聚合矩阵构建算法和对称同态加密技术相结合,在整个训练过程中保护局部训练数据和全局模型免受推理攻击。虽然云服务提供商和参与者之间不需要交互,减少了模型训练开销,但是最终不能确定模型的性能是否满足逻辑回归分类要求。EDEMACU等[11]提出了一个具有低质量数据过滤的多方隐私保护逻辑回归框架,在分布式环境中提出一种度量梯度相似性,用于从具有较差质量数据的数据贡献者中过滤出参数;但是该梯度下降方法和求解逻辑回归模型参数方法不适用于特殊情况,例如数据集是高维稀疏矩阵。
为解决上述问题,文中设计了一个在保证数据质量的情况下用户数据隐私和模型参数隐私保护多分类逻辑回归(Privacy Preserving Multi-classification Logistic Regression,PPMLR)方案,允许云服务提供商与参与者之间交互,使得模型的性能满足逻辑回归分类要求。利用同态加密中的批处理技术和单指令多数据(Single Instruction Multiple Data,SIMD)机制,将多条消息打包成一个密文,并在多个明文时隙上执行相同的算术计算,减少所需的存储空间并优化计算时间。
2 基础技术
2.1 近似数算术同态加密
近似数算术同态加密(Homomorphic Encryption for Arithmetic of Approximate Numbers,HEAAN)是将加密噪声视为近似计算过程中出现错误的一部分,即给定私钥ks和密文模数q,对于小的误差e,一个明文m的加密密文c满足〈c,ks〉=m+e(modq)。减小了一定的精度而大幅提高效率,并支持定点算数,有着出色的运算效率。近似数算术同态加密支持一种并行单指令多数据技术,利用中国剩余定理将多个数据打包到一个多项式中,并在明文槽上提供旋转操作,可以安全地将加密的向量移位成明文向量对应的密文。
近似数算术同态加密是以容错学习(Learning With Errors,LWE)问题[12]为理论基础。 对于2的整数幂N,模数为N的分圆多项式定义为R=Z[X]/(XN+1),对于一个正整数p,R模p的剩余环定义为RP=R/pR。 近似数算术同态加密中提供的主要功能描述如下:
(1) 密钥生成:给定预设的安全参数λ,近似数算术同态加密中默认的最大密文模数p以及离散高斯分布χ,取样s←R,a←Rp,e←χ,输出私钥ks←(1,s)和公钥kp←(b,a)∈Rp×Rp,其中b← -as+e(modp),设P=p2,取样s′←s2,a′←RP,e′←χ,输出计算密钥kev←(b′,a′)∈RP×RP,其中b′← -a′s+e′+ps′(modP)。
(2) 加密(kp,m):输入明文m∈R,取样u←χ,e0←χ,e1←χ,输出密文ct←ukp+(m+e0,e1)(modp)。
(3) 解密(ks,ct):输入密文ct=(ct0,ct1),输出m←ct0+ct1s(modp)。
(4) 加法(ct1,ct2):输入两个密文ct1和ct2,输出ctadd←ct1+ct2(modp)。

(6) 重缩放(ct,bits):重缩放操作将密文的大小降低到适当的级别,新的缩放因子比原始缩放因子小2bits位,但保留ct的相同消息。
(7) 旋转(ct,kr):输入密文ct和旋转密钥kr,输出ct的明文向量旋转r个位置后的密文ct′(包括向左旋转和向右旋转)。
2.2 逻辑回归
逻辑回归广泛应用于二分类任务中,用sigmoid函数估计二元值变量是否属于某一类。 假设用于回归的响应是输入x∈R(1+d)的线性函数,通过sigmoid函数g(z)=1/(1+exp(-z))将整条实线βTx映射到(0,1)。 逻辑回归可以公式化如下:
(1)
其中,向量β∈R(1+d),y∈{±1}是类标签,向量x=(1,x1,…,xd)∈R(1+d)是协变量。
逻辑回归问题可以转化为一个优化问题,其对数似然函数l(β)最多有一个惟一的全局最大值,梯度为0,通过Hessian矩阵的牛顿法求解∇βl(β)=0时的β值。


(2)
由于需要反转加密域中的固定海森矩阵,因此将矩阵H替换为对角线矩阵B,其对角线元素仅为矩阵H中每一行的和,并以特定的计算顺序以更有效地获得B。对于固定海森矩阵矩阵B,其对角元素可以为0,尤其是当数据集是高维稀疏矩阵时,这导致该对角矩阵B不可逆。 为了使简化的固定海森矩阵推广为在任何情况下都是可逆的,应用如下方法:

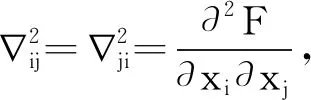
其中,ε是一个较小的正数,以避免被零除(通常设置为1×10-8)。
3 稳私保护多分类逻辑回归方案
稳私保护多分类逻辑回归方案主要分为4个部分,即预处理阶段、数据加密阶段、模型训练阶段和模型返回阶段,图1是系统架构图。

图1 安全多分类系统架构图
3.1 预处理阶段
3.1.1 初始化权重矩阵
在逻辑回归二分类的基础问题上,基于拆解方法中的 “一对其余”(One vs.Rest,OvR)策略[13],扩展二分类逻辑回归模型来解决多分类问题。
给定数据集D={(x1,y1),(x2,y2),…,(xm,ym)},yi∈{C1,C2,…,Ck}。OvR 策略只需训练k个分类器,在训练过程中,每次只把一类样例作为正样本,其他所有样例都作为负样本,这样就会得到k个二分类问题。使用二分类模型对k个数据集可以训练出k个二分类模型,即k个分类器,记为{F1,F2,…,Fk},比较各个分类器的预测置信度,选择最大置信度对应的标记类别作为该样本的预测分类结果。
“一对其余”策略只需要训练k个分类器,相对其它拆分策略,存储和测试时间开销通常较小。使用 “一对其余” 策略得到的多分类逻辑回归的详细过程如算法1所示。
算法1多分类逻辑回归算法。
输入:X∈RN×F,y∈RN,α>0
输出:w∈RN×F
初始化权重矩阵w
for iter=0 toTdo
fork=0 toKdo
fori=0 toNdo
Pi←
Si←σ(Pi)
end
forj=0 toFdo
wkj←wkj-αvj
end
end
end
returnw
3.1.2 客户端数据处理
为了充分利用计算和存储资源,首先将二维训练数据集划分为多个固定大小的矩阵;这些矩阵仍然保留完整的样本信息数据结构,需要预先设置数据矩阵的大小,以便每个矩阵能够以逐行的方式打包成单个密文。如果训练数据集的大小不能被矩阵的这个预设大小整除,则可以将零填充到最后一个矩阵中。然后,将这样一个完整的矩阵逐个打包成一个密文,并对每个密文并行执行操作,这样可以对加密在密文中的明文矩阵的任何元素或任何部分执行同态加密操作。
(3)
可进一步转换为
(4)
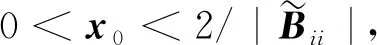

3.2 数据加密阶段
在数据加密阶段,基于近似数算术同态加密方案的开源代码库,定义Secretkey对象可以得到私钥ks,通过私钥ks和环境变量,定义Scheme对象生成公钥kp。 输入明文m,槽的数量slots,批数量batch等参数,调用encrypt(加密)方法加密明文,如算法2所示。
算法2加密。
输入:明文m,槽的数量slots,批数量batch,缩放因子wBits,密文模数log Q,样本数sampleDim
输出:密文ct
步骤1 定义Scheme对象生成公钥kp
/* 调用encrypt方法加密明文m*/
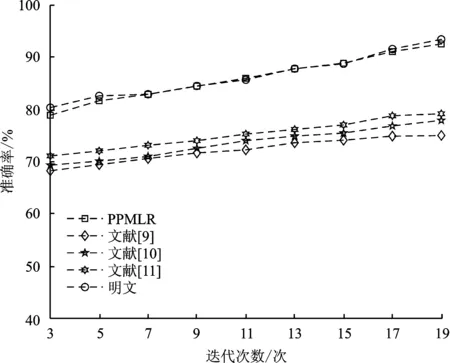
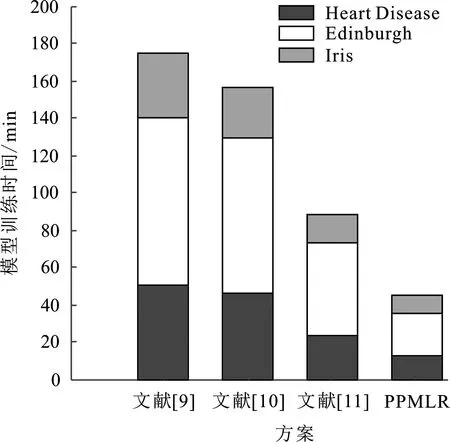
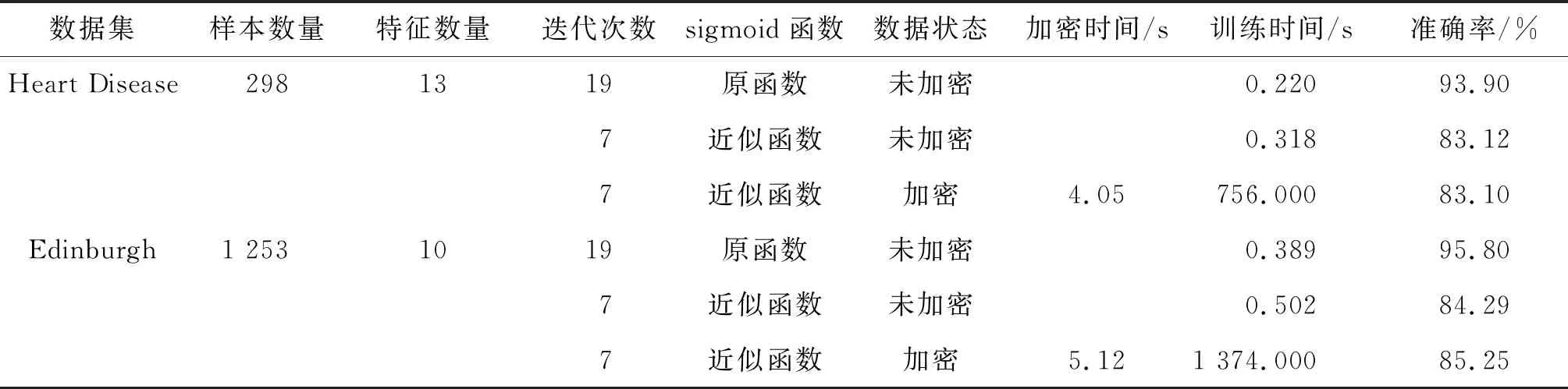
步骤2 for(longj=0;j for longi=0;i m[batchj=1].real(m[j][batchi+1]); ∥real(·)函数用于返回复数的实部 /* 加密得密文ct←slotskp+(m+wBits,log Q)(modp) */ ct=scheme.encrypt(m,slots,wBits,log Q) 数据提供者使用公钥将4个矩阵x0、X、Y、W分别加密为密文ex0、eX、eY、eW。 对这4个数据矩阵加密后,客户端将生成的密文发送到云服务器(Cloud Server,CS)。 云服务器收到加密矩阵后,运行密文域的多分类逻辑回归算法。 由于同态加密的同态性,在密文域上运行多分类逻辑回归算法得到的结果解密后和在明文上运行此算法得到的结果一致。 多分类逻辑回归算法的具体构造如下: 步骤1 在收到数据提供者上传的密文后,云服务器在eX和eY之间执行单指令多数据乘法以获得密文eZ。 在剩下的训练过程中,云端不再需要密文eX和eY。 步骤3 云端对接收到的密文ex0和得到的密文eB进行运算,调用迭代公式(4),得到密文eB-1加密B的逆近似。 步骤4 云端通过对密文eZ和权重密文eW的同态加密操作计算出原始梯度密文eg。其计算过程如下: 云端接受两个密文eZ和eW,并评估梯度下降算法以找到最佳建模向量。 每次迭代的目标是使用损失函数梯度更新权重密文矩阵eW的建模向量W(t): (5) 其中,αt表示第t次迭代时的学习速率,每次迭代包括以下8个过程: (1) 对于给定的两个密文eZ和eW,将它们相乘并按p位重新缩放: (6) 输出密文如下: e2←Add(e1,Rotate(e1;2j)) , (7) 对于j=0,1,…,log(f+1)-1,输出密文e2加密第一个列和其他列中的一些“垃圾”值,其中“垃圾”值用*表示: (3) 执行常量乘法以消除垃圾值。 通过计算编码多项式cm←Encode(C;pc)对矩阵进行编码: 对某些整数pc使用2pc的比例因子。 选择参数pc作为明文的位精度,将多项式cm乘以密文e2,并用pc位重新缩放: e3←ReScale(CMult(e2;cm);pc) 。 (8) 输出密文e3在第一列中是内积结果,在其他列中用零填充: (4) 将内积值复制到其他列,与②类似,通过将输入密文添加到其列中来实现递归移位,但方向相反: e4←Add(e3,Rotate(e3;-2j)) 。 (9) 对于j=0,1,…,log(f+1)-1,输出密文e4每行内积值相同: (6) 云端将密文e5与加密数据集eZ相乘,并将所得密文重新缩放p位: e6←ReScale(Mult(e5,eZ);p) 。 (10) e7←Add(e6,Rotate(e6;2j)) 。 (11) 对于j=log(f+1),…,log(f+1)+logn-1,输出密文矩阵如下: e8←ReScale(Δ(t)·e7;pc) , (12) (13) 最后,返回加密更新的建模向量的密文。 步骤5 云端通过在密文eB-1和eg之间的一次单指令多数据乘法,生成密文eG。 步骤6 云端对不同的算法使用不同的学习速率设置策略,使用密文eG更新权重密文eW。 步骤7 在每次迭代结束时,云端检查权重密文eW的剩余模是否足够大,以完成下一轮密文eW更新。 否则,云将使用旋转键引导这些权重密文,以大模数呈现权重密文。 步骤8 如果算法达到预设的最大迭代次数t,则云服务器向数据提供者发送权重密文,否则训练过程转到步骤4继续运行。 通过上述8个步骤,执行了内积计算、sigmoid函数多项式近似、重缩放、移位等操作,完成了密文运算,即密文的多分类逻辑回归算法。 整个训练过程完成后,云服务器将密文训练模型发给数据提供者,数据提供者解密密文训练的结果,并确定模型的性能是否满足要求。如果是,停止训练。否则,继续训练。其中训练模型的性能满足要求的标准为:模型的准确率是否与未加密情况下的准确率近似,且准确率是否高于之前的方案,同时判断运行时间在某些注重隐私保护的领域中是否属于可接受范围内。 在半诚实对手模型[14]中,假设数据提供者和云服务器持有公钥kp,数据提供者持有私钥ks。 对于稳私保护多分类逻辑回归方案的评估确定性函数f,分析其安全模型,即数据提供者加密其私有数据x并将结果发送给云服务器。 云服务器对加密结果执行同态操作以获得y,同态评估密文模型函数,数据提供者解密y并获得f(x)。 定理1假设云服务器是一个半诚实实体,并假设数据提供者和云服务器不相互勾结。x是数据提供者的私有数据。如果同态加密方案提供了语义安全性[15],那么在对x执行同态运算并对密文求评估函数后,数据提供者获得f(x),云服务器什么也不能获得。 安全证明:假设稳私保护多分类逻辑回归的安全性证明遵循基于仿真的范式。 设数据提供者和云服务器在评估期间的视图分别为VDP和VCS,云服务器的视图VCS由{kp、x、y、f(x)}组成。 首先同时构建一个模拟器SCS,SCS随机选择输入数据{x′、y′、f(x′)},然后SCS通过V′CS={kp、x′、y′、f(x′)}模拟VCS;由于同态加密方案提供语义安全性,因此VCS和V′CS无法区分,即稳私保护多分类逻辑回归对半诚实云服务器是安全的。 云服务器能够得到加密数据集D′和密文矩阵,本节证明在半诚实模型下,云服务器在得到加密数据集D′以及密文矩阵时无法恢复出明文集合D={x1,x2,…,xn}。 首先,密文ci对应的明文为xi,其中i=1,2,…,n;为了便利,简化加密过程为c=HE.E(x,S),其中HE.E(·)表示调用同态加密中加密函数,S为密钥。因此可以推论当同态加密自身是安全且云服务器无法获取密钥时,那么明文数据集就是安全的。 当然也可假设密钥在数据提供者的私有云存储,且公共云无法获取私有云信息。 其次,构建特殊矩阵U来构造密文下的损失函数,通过等式I*=AM求解出矩阵A(其中M是密钥转换矩阵),然后通过矩阵A来构造矩阵U=ATA;由于密文和明文之间满足关系c=M(ωx)*,因此当云端拥有矩阵U和密文c时,可能会通过以上3个等式联合求解明文。 但是,对于一个随机的正定矩阵Q,满足关系QTQ=I,其中I为单位矩阵。 于是可得到等式U=ATA=ATQTQA=ATIA=U。 很明显,不能从U=ATA中恢复出矩阵A,因为矩阵Q是随机选取的。 因此云服务器无法从密文c和矩阵U中恢复出明文。 稳私保护多分类逻辑回归方案在功能上分别与文献[9-11]进行对比,如表1所示。 文献[9]使用同态加密技术来保证特征数据和标签信息的安全,但是没有对非线性函数使用多项式近似计算;文献[10]可以在整个训练过程中保护局部训练数据和全局模型免受推理攻击。虽然云服务提供商和参与者之间不需要交互,减少了模型训练开销,但是最终不能确定模型的性能是否满足逻辑回归分类要求;文献[11]在模型训练过程中过滤掉质量较差的数据。但是该梯度下降方法和求解逻辑回归模型参数方法不能适用于任何情况。稳私保护多分类逻辑回归方案可以解决多分类问题,用多项式近似值代替sigmoid函数,将二维训练数据集划分为多个固定大小的矩阵;这些矩阵仍然保留完整的样本信息数据结构,在模型训练期间,能够减轻数据的稀疏性,保证数据质量。 表1 方案功能比较 文中所有的实验都在Intel Core i7-8750H 2.20 GHz机器上实现。使用了来自加州大学欧文分校(University of California Irvine,UCI)数据库的Heart Disease、Edinburgh 、Iris 3个数据集、Heart Disease数据集,共298个样本,每个样本包含13个特征;Edinburgh数据集共1 253个样本,每个样本包含10个特征;Iris数据集共150个样本,每个样本包含4个特征。 为验证方案的分类性能,分别在Heart Disease数据集、Edinburgh数据集上对稳私保护多分类逻辑回归方案和文献[9-11]的方案进行了准确率对比实验,采用5倍交叉验证方法来获得实验结果的有效性,最大迭代次数λ取19。从图1和图2中看到使用sigmoid原函数进行计算时,通过增大迭代次数,可以达到较高的准确率,同样使用sigmoid近似函数进行计算时,方案对加密数据训练得到的准确率与对未加密数据训练得到的准确率几乎相同,且高于其他方案的分类准确率。 由此可以验证本方案同态计算的可行性和准确性。 图1 Heart Disease数据集精度 图2 Edinburgh数据集精度 本小节测试了稳私保护多分类逻辑回归方案与文献[9-11]的方案在3个数据集上完成加密和模型训练所需要的时间开销;图3和图4反映了每个方案的计算时间开销对比情况。根据实验结果,从加密时间来看,在Heart Disease数据集下,所提模型的加密时间比文献[9-11]分别减少了约61.65%、52.03%、37.98%,在Edinburgh数据集、Iris数据集下,加密时间也减少了。用户只参与最终密文预测结果的解密计算,没有参与密文训练过程,所以用户的解密计算时间开销不会随数据集的样本和特征数的增加而增加。在大规模训练数据集上,稳私保护多分类逻辑回归方案在对多项式的近似、数据集的划分、执行具体的同态加密操作等步骤中充分利用计算和存储资源,对于医疗、财务、个人信息等隐私数据而言,该模型的效率是较好的。 图3 数据集上加密时间和对比 图4 数据集上模型训练时间和对比 根据上述的实验分析,表2列出了在Heart Disease数据集,Edinburgh数据集上分别对未加密数据和加密数据进行计算的模型的性能,由于迭代次数越大,计算开销也越大,将加密状态下的迭代次数设置为7次。对实验中的加密时间,模型训练时间以及准确率进行计算和统计。 表2 使用5倍交叉验证的模型的实验结果 文中提出了一种在加密的训练数据上实现多分类逻辑回归的方案,使数据所有者能够利用云服务提供商的强大存储和计算资源进行多分类逻辑回归分析,而不暴露训练数据的隐私,利用同态加密中的批处理技术和单指令多数据机制来加快训练进度;同时该方案能够保证训练数据的质量,在不影响多分类数据准确率的同时降低了计算开销。通过性能分析和实验对比,在真实数据集上进行模拟,该方案综合性能较好。3.3 模型训练阶段

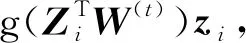

3.4 模型返回阶段
4 安全性分析
4.1 语义隐私性
4.2 数据隐私性
5 性能分析
5.1 功能对比

5.2 损失分析

5.3 计算开销分析

6 结束语

