面向流量预测的时间相关图卷积网络构建方法
张可涵,李红艳,刘文慧,王 鹏
(1.西安电子科技大学 综合业务网络理论及关键技术国家重点实验室,陕西 西安 710071;2.淘宝(中国)软件有限公司,浙江 杭州 311100)
1 引 言
在全球数字经济快速发展的变局下,数字技术已经成为了各国基础建设的重要发展目标之一。2022年我国大力推行了“东数西算”工程,通过构建数据中心、云计算、大数据一体化的新型算力网络体系,优化数据中心建设布局,促进东西部协同联动[1]。由此可见数据中心网络作为数据传输、计算和存储的中心[2],是数字经济时代最重要的基础设施之一。据统计,全球超大规模数据中心数量已增至659个,而我国政府、企业、教育机构等拥有各类数据中心机房约7.4万个,约占全球数据中心总量的23%[3]。随着数字经济的快速发展,数据中心市场高速增长。
数据中心网络中核心业务场景为计算任务。该类任务请求多以虚拟网络形式存在,即通过将数据中心网络中的计算任务拆分成多个子计算任务,支持将不同计算子任务部署在不同的服务器节点执行分布式并行计算[4-5]。相比于将全部任务部署于同一个节点进行计算,分布式并行计算可大大压缩任务的计算时延,提升用户的体验。此外,虚拟网络技术[6-9]支持数据中心计算资源、存储资源和网络资源的共享[10],可有效提升数据中心资源利用率和网络吞吐量,降低网络运营成本。具体地,数据中心虚拟网络由节点和链路构成,节点代表计算子任务,每个子任务对所部署的服务器节点有计算能力要求,用Flops衡量[11];链路代表子任务间的通信需求,可用链路通信速率衡量。进而,数据中心网络部署计算任务的过程称为虚拟网络映射,即将虚拟网络中节点部署于满足其计算能力需求的服务器容器中,不同节点所部署容器之间连接的网络容量(即端到端带宽)需满足该子任务间的通信需求。在虚拟网络中,每个子任务会处在不同服务器的虚拟机中,根据虚拟机编号可以查找出一个业务下的所有子任务,据此构建一张业务虚拟网络拓扑图。如图1所示,一个计算任务下涵盖5个子任务,将计算任务映射于数据中心的服务器中,虚线代表该子任务映射于所指向服务器的容器中,最终这些子任务按序或并发执行。事实上,由于虚拟网络流量预测精度欠佳,虚拟网络映射多依据业务需求的峰值进行资源分配,制约了数据中心资源利用率[12-15],阿里巴巴集团控股有限公司中数据中心计算资源利用率仅约为39.28%[16],亟需提出高效精准的虚拟网络业务预测模型,支撑数据中心网络资源的高效分配,提升数据中心网络的资源利用率。

图1 业务虚拟网络拓扑图
目前,大部分数据中心网络流量预测工作集中在单链路流量预测领域,但由于链路之间的通信带宽需求会相互影响,单链路预测难以捕获不同链路间的关联关系,导致预测精度难提升。文献[17]提出了基于卷积神经网络(Convolutional Neural Network,CNN)的网络流量预测方法,将网络流量的时间序列转换为图像,用卷积核来捕获流量特征。由于卷积神经网络的卷积核大小有限,难以捕获长周期序列的相关特征[18]。基于此,文献[19]提出了循环神经网络(Recurrent Neural Network,RNN)模型,在隐藏层的神经元之间建立连接,表征了神经元的当前状态与历史状态之间的关系,易于捕捉较长周期序列的相关特征,由于神经网络固有的梯度消失的问题,RNN神经网络仍然无法精准预测长周期序列。文献[20]等提出了基于长短期记忆网络(Long Short-Term Memory,LSTM)流量预测方法。与RNN网络相比,LSTM网络中的神经元增加了3个门结构,用于控制历史信息在隐藏层中的传播方式,在一定程度上避免了梯度消失问题。
虚拟网络环境中,由于任务之间的相关性,链路流量不仅与本链路的历史信息相关,还与网络中的其他链路流量相关。图2刻画了不同链路上的通信流量大小随时间变化的曲线,如图2(a)和图2(b)所示,容易发现两条链路的流量趋势呈现明显的相关性,即当图2(a)中的曲线在20~30时刻上升时,图2(b)中的曲线也在30~40时刻内出现上升趋势。因此,充分挖掘链路流量之间的空间相关性和时间相关性信息,是提升数据中心网络流量的预测精度的关键。
事实上,图神经网络(Graph Neural Network,GNN)[21]具备从图中提取节点间相关关系的能力。当前用于预测的两种热门图神经网络:图注意力网络(Graph Attention neural Network,GAN)[22]和图卷积神经网络(Graph Convolutional Network,GCN)[23-24],两者都能够挖掘并利用不同链路之间的空间相关性。其中,GAN网络是在GCN网络基础上进行改进所提出的模型,适用于动态图的建模,但在虚拟网络中一个业务下分割的子任务数往往是固定的,即网络的节点数是不变的,且所构成的网络规模较小,而GAN网络参数比GNN网络和GCN网络更多,计算复杂度更高,并不适用于小型网络的建模。而对于传统的GCN网络,由于其难以学习节点的时间特征,往往需要和其它时序模型进行结合。文献[25]提出了时间图卷积网络,利用图卷积神经网络GCN捕获道路间的流量关系,利用门控循环神经网络(Gated Recurrent Unit,GRU)[26]提取道路流量的时间序列特征。然而,时间图卷积网络只能提取某一时刻下链路间的时间特征,难以表征链路之间的异步关系,即链路之间在一定时差下的相关性。因此,尽管GCN网络以及基于时间的GCN网络可有效挖掘网络中不同链路的相关性,将传统GCN网络以及基于改进的CCN网络应用于虚拟网络流量预测,仍面临如下挑战:①虚拟网路各任务的启动可能存在先后顺序,而GCN网络假定图中各节点同步,忽略了虚拟链路之间的异步特征,导致预测模型精度低;②GCN固定长度的卷积核难以捕获不同时段的流量特征,如图2(a)所示,0~80时刻内,流量随时间上升且波动较小;80~240时刻内,流量随时间剧烈抖动,若采用相同长度的卷积核,难以匹配该流量的实时变化情况,使得不同时段预测精度差距较大。

(b) 任务1与任务3之间的通信流量
针对上述问题,笔者提出了一种时间相关图卷积神经网络(Temporal Correlation Graph Convolutional Network,TC-GCN),通过充分挖掘虚拟网络各链路间的时间和空间相关性,以及利用不同时间窗口长度的GCN网络进行联合学习,精准预测了虚拟网络各链路的流量。首先,利用皮尔逊相关系数的流量相关性分析方法,分析虚拟网络各链路流量之间的时间关系,解决了虚拟网络链路间由于流量异步性导致的预测偏差,据此提出了具有时间属性的GCN网络邻接矩阵,并设计了时间相关GCN神经网络,实现链路相关性的精准表征;其次,分别构建长窗口/短窗口时间相关GCN神经网络,作为序列特征的训练模型,用于学习流量序列平滑段和波动段,以此匹配流量在不同时段的特征,有效避免了神经网络对于长序列学习后的梯度消失问题;最后,设计了一个误差加权单元(Error Weighted Unit,EWU),依据长窗口、短窗口GCN网络模型的预测精度,构建长短窗口GCN网络输出值的加权系数,提升虚拟网络的流量预测精度;利用反向传播算法学习时间GCN网络、误差加权单元的参数,构成虚拟网络流量预测模型TC-GCN。在数据中心所产生的真实数据集上,设计了数值仿真实验,验证了TC-GCN模型的流量预测精度高于传统GCN网络。文章最后总结了文中工作,讨论了后续的研究工作。
2 虚拟网络链路相关性分析
如图3(a)所示,虚拟网络可以用图F进行表征,图中的节点为计算任务节点,节点间的链路为虚拟链路,仅承载任务节点之间的流量。为方便GCN网络进行计算,这里将图F映射为链路流量关系图G,如图3(b)所示,图中的节点vi对应虚拟网络中的链路li,若虚拟网络中的两条边为邻接关系,如边l1和边l2,则在链路流量关系图中v1与v2亦为邻接关系。

图3 虚拟网络与链路流量映射关系
(1)

节点v1与v2,v3与v4的皮尔逊相关系数分别如图4(a)和4(b)所示。在图4(a)中,可以观察出v1与v2这两个节点的相对时刻为5时,虚拟网络两条链路的相关性最大。链路流量相关性随着相对时刻的增加而降低,各链路之间的相关性存在差异。图卷积神经网络依据链路之间的相关性预测链路流量,若链路流量相关性与序列的相差时刻有关,图卷积神经网络的邻接矩阵需考虑序列的时间因素。
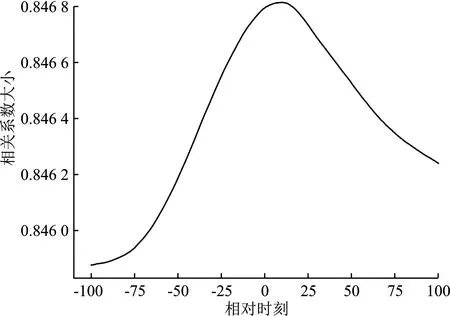
(a) 图3(b)中节点v1与节点v2之间的相关系数

(b) 图3(b)中节点v3与节点v4之间的相关系数
3 时间相关图卷积网络流量预测方法
3.1 时间相关图卷积神经网络流量预测
这里提出了时间相关图卷积网络架构。如图5所示,TC-GCN由两个时间相关图卷积神经网络和一个误差加权单元构成。设计了两个时间相关图卷积神经网络TC-GCNl和TC-GCNs,其中TC-GCNl将包含较长时刻l的节点特征矩阵输入TC-GCN进行图卷积运算,TC-GCNs将包含较少时刻s的节点特征输入TC-GCN进行图卷积计算。两者分别表征业务流量不同时段的缓变与剧烈波动特征。TC-GCNl用于匹配流量的缓变特征,TC-GCNs用于匹配流量的剧烈波动特征。误差加权单元对两个图卷积神经网络的输出进行加权求和,旨在提升预测精度。与传统图卷积神经网络相比,时间相关图卷积神经网络中的邻接矩阵引入了链路流量的时间相关性,精准表征了链路流量之间的关联关系。

图5 TC-GCN网络结构
3.2 时间相关图卷积神经网络
虚拟网络中各计算节点联合承担大型计算任务,各计算节点所承载子任务不同,导致各链路流量存在时间偏差和特征偏差,基于此,文中提出了时间相关图卷积神经网络,如式(2)所示。其中,Xt∈RN×M表示t时刻上N条链路流量的特征矩阵,每条链路的流量窗口长度为M个时刻。参数矩阵W用于提取链路流量序列的特征,W∈RL×M,W由M个卷积核构成,L为卷积核长度,通过训练W提取链路流量的序列特征。
Y=ReLU(ADRXtW) 。
(2)
ADR∈RN×N表示N条链路流量之间的时间相关矩阵,用于替代传统的图邻接矩阵。按照式(1)计算出每条链路之间的最大时间相关系数,采用softmax激活函数对所得相关系数进行归一化处理,旨在对每条链路流量与其他所有链路流量之间的相关系数按照总和为1分配权重,如式(3)、(4)所示。归一化后所得即为时间相关矩阵ADR的参数。
(3)
(4)
为了学习流量的不同局部时间特征,TC-GCN由两个不同输入窗口长度的GCN组成:长窗口图卷积网络TC-GCNl捕捉流量曲线中变化相对平缓的时间特征,短窗口图卷积网络TC-GCNs捕捉流量曲线中变化相对剧烈的时间特征,两者都可以学习到流量的空间相关性。计算公式如下所示:
(5)
(6)
3.3 误差加权单元
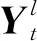
(7)
(8)
(9)

图6 误差加权单元结构
其中,Wl和bl代表TC-GCNl预测误差的参数和偏置量,Ws和bs代表TC-GCNs预测误差的参数和偏置量,xi为误差大小。另外,激活函数NegR将各模块预测值的输出权重定义为一种与误差负相关的关系,即误差越大则为相应预测结果分配的权重越小,误差越小则为相应预测结果分配的权重越大,且两个输出权重之和为1。这样做的目的是尽可能使得误差小的预测结果成为决定最终预测值的主导方,使得误差大的预测结果对最终预测值的影响尽可能小。
最后,将两个模块的预测值按照输出权重进行加权求和,得到最终结果Yt+1输出,计算公式如下所示:
(10)
其中,ol和os分别代表TC-GCNl和TC-GCNs的输出门权重系数。误差加权单元EWU通过对TC-GCNl和TC-GCNs两个模块的预测值加权求和,生成时间相关图卷积网络TC-GCN的预测值,如此构成时间相关图卷积网络TC-GCN。
3.4 损失函数
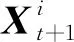
(11)
4 仿真实验
4.1 实验数据
实验数据集为2021年9月从3所大学的数据中心采集,其中包括1 980台服务器,这些服务器部署于北京,每5 min采集一次,采集时长为8 d。收集的数据中包括时间戳、流量优先级、到达和处理时间、容器Pod编号与源端口和目的端口。数据文件内包含1 040 000多条流量累计数据,总大小为2.7 GB。根据任务编号和执行时间可分析出虚拟网络的拓扑结构,从而构建出相应的图结构。实验选取前80%的流量序列作为训练集,剩下20%的流量序列作为测试集。
4.2 实验设置
4.2.1 基线模型
文中选择以下5种对比模型。
差分整合移动平均自回归模型(Auto Regressive Integrated Moving Average model,ARIMA)[27]:为线性预测模型。
长短期记忆网络(LSTM):通过3个门结构控制信息的更新与传播,适用于时间序列预测。
图卷积神经网络(GCN):对图数据进行操作的神经网络架构,适用于存在空间特征的序列预测。
时间图卷积神经网络(T-GCN):通过GCN提取时间特征,通过GRU提取空间特征。
时空图卷积神经网络(STGCN)[28]:通过多个时空卷积模块进行特征提取,其中,时间模块由一个一维卷积核与一个GLU组成,空间特征由图卷积神经网络提取。
4.2.2 实验环境
实验使用Python3.7基于Pytorch1.0.1实现,实验的编译和测试均在Windows10系统下,使用CPU Inter(R)Core i3-7100 @ 3.90 GHz,GPU的型号是NVIDIA GeForce GTX 1050,内存8 GB。在实验中使用了Facebook公司的Pythorch框架对神经网络模型进行编写,相比于TensorFlow,PyTorch网络定义方便,更有利于研究小规模项目快速做出原型。实验中,设置学习率learning rate=0.001,batch_size参数m=64,训练次数epoch=50。
4.2.3 评价指标

准确率RAccuracy
(12)
平均绝对误差RMAE
(13)
均方根误差RRMSE
(14)
其中,RAccuracy值越大,预测性能越好;RMAE和RRMSE值越小,预测性能越好。
4.3 实验结果分析

表1 不同模型预测虚拟网络流量的性能
如表1中的结果所示,文中提出的时间相关图卷积网络TC-GCN性能较其它4个基线模型有较明显提升,证明文中模型更加适用于数据中心虚拟网络流量预测。
通过指标数据很容易观察到不同基线模型在预测虚拟网络流量时的性能差异;结合真实数据,根据各个模型的预测结果分别绘制相应的曲线图,如图7(a)所示。可见,传统的统计方法ARIMA表现不佳,预测值在数据上升阶段容易超出峰值,在数据下降阶段容易低于峰谷,主要是由于线性方法很难处理复杂的、非平稳数据。GCN在对时间序列数据进行预测时,可以大致学习出数据的变化趋势,但很难准确拟合真实曲线,极有可能的原因是其难以学习数据复杂的时间特性,以及相邻链路流量时间相关性。LSTM的预测性能优于ARIMA和GCN,但相较组合模型STGCN和T-GCN显现出较大的劣势,这主要是因为实验数据采集于数据中心网络,受到网络拓扑结构的影响较大,相邻链路的流量数据会直接影响预测结果,而LSTM无法明确捕捉并利用到这些空间特征进行有效预测。STGCN也是基于迭代预测机制的组合模型,但是更多的网络结构层导致其比TC-GCN引起更多的误差累积,其使用一阶门控卷积单元学习数据的时间特征,也远不及T-GCN的时间特征学习能力,同时也未考虑相邻链路数据的时间相关性,对于流量峰值的预测还不够准确。而T-GCN也因为针对的是同一时刻的流量数据,忽略了不同时刻的时间关系,存在一定的时刻偏差,所以对于虚拟网络的流量预测不精确。因此STGCN和T-GCN的预测性能相对逊色于TC-GCN的预测性能,如图7(e)和图7(f)所示。

(a) Arima预测结果图
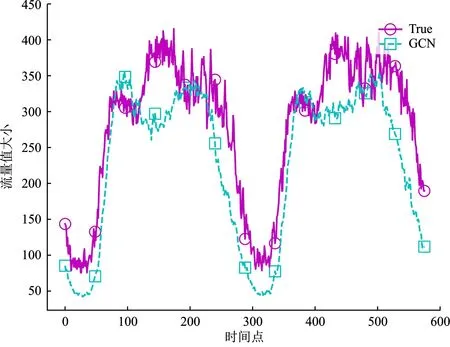
(b) GCN预测结果图

(c) LSTM预测结果图

(d) STGCN预测结果图
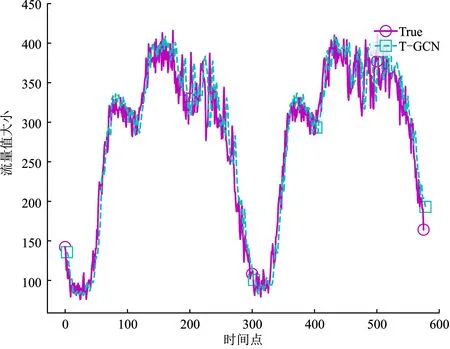
(e) T-GCN预测结果图

(f) TC-GCN预测结果图
时间相关图卷积网络TC-GCN中添加了基于皮尔逊相关系数的相关性分析方法,不仅通过GCN计算相邻链路在相同时刻的空间相关性,也能计算相邻链路在不同时刻或时间段的时间相关性,充分捕捉了时空相关性对流量曲线波动的影响;另外,TC-GCN分别使用两种GCN模块捕捉流量的时间特性,通过输入不同时间窗口的节点特征矩阵,训练模型提取流量的长期特性和短期特性,其中短期特性对应着业务虚拟网络流量值变化相对剧烈的时段,这样也可以使得模型对于峰值的预测更加精准,并且能够拟合流量曲线的包络。这样的预测结果对于数据中心资源分配工作具有更加重要的现实意义,当分配的资源能够满足需求最大值时,也就能保障业务整体的QoS。
5 结束语
笔者提出了时间相关图卷积神经网络,利用皮尔逊相关系数,构建了具有时间属性的GCN网络邻接矩阵,精准表征了链路之间的相关性;设计了长/短窗口GCN加权的流量预测机制,利用不同的窗口长度匹配流量序列在不同时段的缓变与波动特征,提升了虚拟网络的流量预测精度。利用数据中心所生产的真实数据验证了所提模型的有效性。可见依据流量特征对GCN网络进行改进,有助于提升神经网络的可解释性,降低神经网络的规模,提升神经网络在在线流量预测中的适用性。在下一步工作中,将进一步改善GCN网络的邻接矩阵,并考虑动态图建模的情况,结合图注意力网络,嵌入式图卷积网络等结构,以提升流量预测的精度。

