基于PSO-RBF优化的船舶六相推进电机缺相故障新型自适应滑模容错控制研究

施伟锋,朱倍志,谢嘉令

(上海海事大学 物流工程学院,上海 201306)

0 引 言

船舶电力推进系统推进用电和船舶负载用电合一,可减小推进装置空间占比、提高船舶电力系统供电稳定性且降低船舶运行时能源管理难度,是船舶控制系统智能化的主要发展方向[1]。六相永磁同步电动机(six phase permanent magnet synchronous motor,SPPMSM)具有输出功率高、谐波失真小、故障容错高、电机结构紧凑、易于控制等特点,是船舶电力推进电机的理想选择。

船舶电力推进系统中设备繁多,工作环境复杂,如在风浪较大的情况下船舶会发生剧烈摇摆,使推进装置工作环境恶化,使船舶电力发生故障,影响船舶运行[2]。文献[3]通过分析电机故障时自由度的损耗,提出了一种通用容错电流计算表达式,保证了电机故障后平稳运行,降低了容错控制复杂度;文献[4]提出了一种使用模型预测电流的容错策略,通过重构故障后解耦矩阵从而得到新的预测模型,提高了容错控制性;文献[5]基于故障后电机的数学模型,对传统的电流环结构进行改造,设计一种双层电流环结构,使故障后电机系统可更加完全的解耦,提高了电机控制的稳定性。综上,针对永磁同步电机断相后容错策略,大致可以分为2类:① 通过对故障后剩余健康相电流进行补偿,保证故障前后定子绕组生成的磁动势不变;② 采用新型旋转坐标,建立新的电机数学模型,使故障后的电机模型在新坐标系下解耦,实现电机容错控制。

目前永磁同步电机矢量控制系统中,普遍采用PI调节器作为速度控制器,但对非线性、强耦合的六相永磁同步电机来说,当控制系统受到环境干扰或者电机内部参数变动影响时,PI控制方法并不能满足实际控制需求。响应速度快、不易受到扰动和参数影响的滑模控制(sliding mode control,SMC)容易满足电机的控制需求[6]。文献[7]提出了一种基于改进变指幂次数趋近律的滑模控制器,通过新型趋近律提高了运动点的趋近速度,提高了系统控制性能;文献[8]提出一种模糊规则与指数趋近律相结合的混合滑模控制策略,对滑模控制器的趋近律参数进行实时调整,提高了控制性能;文献[9]通过神经网络优化滑模控制中的切换增益,实现了对负载变化以及外界扰动影响的实时补偿,提升了电机控制系统稳定性。

相关研究在不同程度上提高了运动点趋近速度,抑制了滑模控制中的抖振现象,但未考虑永磁同步电机在断相故障下的容错控制。因此,笔者在传统的船舶推进电机滑模控制基础上,提出一种针对推进电机缺相故障下RBF神经网络与滑模控制相结合的容错控制策略,利用神经网络对SMC中的切换增益进行实时调整,并通过粒子群算法的全局寻优能力对RBF神经网络的权值、中心向量及宽度进行优化,同时引入新型指数趋近律和自适应律提升滑模控制性能,以保证船舶推进电机在缺相故障状态下的稳定运行。

1 六相推进电机模型

船舶电力系统主要由发电单元、配电单元、电力推进单元及其他负载单元组成,其中电力推进单元容量约占船舶电网容量的3/5[10]。

船舶电力推进系统通常由推进电机、变频器和螺旋桨等设备组成,螺旋桨是船舶航行的主要动力源[11]。现代船舶典型电力系统结构如图 1 。

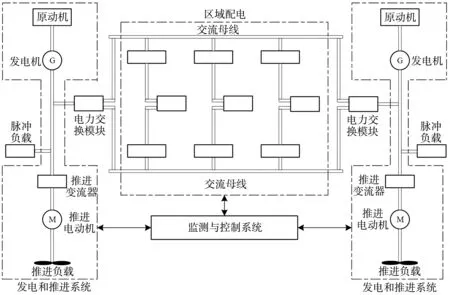
图1 船舶电力系统结构Fig. 1 Structure diagram of ship power system

相较老式船舶机械推进单元,现代船舶电力系统结构更为复杂,船舶设备都依靠电源,这使各种设备出现故障的概率增加。现代船舶电力推进系统各用电负载间的联系更为紧密,如发生故障,可能会导致其他健康设备也受影响[12]。

船舶SPPMSM在理想状态下电压方程如式(1):

(1)

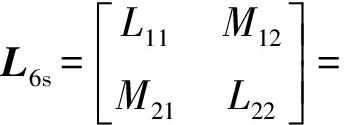
λ6s=[sinθesin(θe-2π/3) sin(θe-4π/3) -sin(θe-π/6) sin(θe-5π/6) sin(θe-3π/2)]T;u6s=[uAuBuCuUuVuW]T;i6s=[iAiBiCiUiViW]T;ψ6s=[ψAψBψCψUψVψW]T;R6s=diag[RRRRRR]。

当电机正常运行时,通过式(2)～式(4)坐标变换(忽略零序分量的影响),得到基于双d-q坐标变换的同步电机电压和磁链方程如式(5)、式(6):

(2)

P1=

(3)

P2=

(4)

(5)

(6)

式中:ud1、ud2、uq1、uq2、id1、id2、iq1、iq2为电机在d-q轴上的电压与电流分量;ψd1、ψd2、ψq1、ψq2为电机的磁链;Ldd=1.5LAAd,Ld=Ldd+LAA1,Lqq=1.5LAAq,Lq=Lqq+LAA1;LAAd、LAAq为绕组d轴和q轴自感系数;LAA1为漏自感系数。

此时电磁转矩方程可写为:

Te=1.5Pn(iq1ψd1-id1ψq1+iq2ψd2-id2ψq2)

(7)

式中:Pn为电机极对数。

2 优化的自适应滑模容错控制

2.1 船舶推进电机新型自适应滑模控制

SPPMSM的运动方程和经简化后的转矩方程如式(8):

(8)

式中:TL为负载转矩;B为阻尼系数;ωm为机械角速度;J为转动惯量。

定义SPPMSM状态变量如式(9):

(9)

式中:x1、x2为状态变量;ω*为设定转速。

将式(8)与式(9)联立得:

(10)

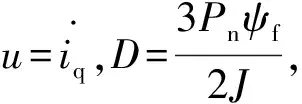
(11)

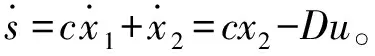
笔者引入一种新型的指数趋近律如式(12):

(12)

式中:0<δ<1;a、b、q为大于0的常数;σ>0。

由式(12)可知:当|s|的值很大时,f(s)近似为1/δ,g(s)近似为1,-εf(s)·g(s)为大于ε的数,运动点趋近滑模面的速度较传统指数趋近律快;当|s|逐渐减小时,f(s)逐渐趋向1,-εf(s)·g(s)逐渐趋近于0,使得滑模运动的运动轨迹由带状变为渐进收敛至0的形状,优化了与滑模面之间的趋近运动,并使运动系统快速收敛,削减了系统抖振。

为减小故障对控制性能的影响,同时针对断相故障导致的系统不稳定,需设计一种自适应律来抑制扰动并优化控制器在故障下的控制性能,设计自适应律为:

(13)

式中:μ、γ为常数。

故由式(8)～式(13)得到控制器方程与q轴参考电流为:

(14)

2.2 基于PSO-RBF优化的新型自适应滑模控制

2.2.1 RBF神经网络滑模控制器

为优化滑模控制性能,削减系统抖振,利用RBF神经网络的学习与自适应能力对SMC中的切换增益进行实时调整,算法如式(15):

(15)

(16)

故神经网络权值最终学习算法如式(17):

w(t)=w(t-1)+Δw(t)+α[w(t)-w(t-1)]

(17)

式中:η为神经网络学习速率;α∈(0,1)为惯量系数。笔者取η=0.1,α=0.05。

将式(15)的输出结果带入式(14)中,得到基于RBF神经网络的SMC方程与q轴参考电流:

(18)

2.2.2 PSO优化原理

神经网络输出结果主要受w、Cij和bi影响,故通过粒子群算法(particle swarm optimization,PSO)的寻优能力来优化神经网络参数,进一步提升控制系统性能。

设置第n个粒子位置pn和速度vn为:

pn=[b1b2b3C11C12…C23w1w2w3]

(19)

vn=[vn1vn2vn3…vn12]

(20)

粒子经过t次迭代后的个体极值inbest(t)和全局极值gbest(t)为:

(21)

粒子位置及速度的更新公式为:

(22)

式中:W为惯性权重,且W=0.1;c1、c2为学习因子,且c1=c2=2;r1、r2均为服从均匀分布U(0,1)的随机常数。

经计算,粒子个体极值和全局极值更新为:

(23)

gbest(t+1)=min{y[inbest(t+1)]}

(24)

式中:y(x)为粒子适应度函数,且

(25)

式中:Nd(t)为期望输出;N(t)为实际输出。

综上,基于PSO-RBF优化的新型自适应滑模控制框图如图(2)。

2.3 船舶推进电机缺相容错控制

在船舶运行期间,推进同步电机常见的逆变器与电机的开路、短路问题均可利用故障隔离技术转为断路运行状态。以SPPMSM为研究对象,根据故障前后定子磁势不变原则,设计单相断路故障容错策略。

SPPMSM正常运行时,其定子电流会在气隙中生成一个可与转子磁场相互作用的旋转磁势,进而产生可驱动电机正常运行的稳定电磁转矩。电机出现缺相故障后,定子电流产生的旋转磁势会由稳定的圆形磁势分解为多个旋转磁势,这些磁势都会与转子磁场相互作用,产生导致合成转矩发生剧烈波动的额外不平稳转矩[13]。基于定子磁势不变的容错控制策略,就是通过调节故障后剩余健康相的电流幅值与相位,补偿缺相造成的磁势变化,保证电机稳定运行[14]。

当SPPMSM正常运行时,各绕组产生磁势为:

图2 基于PSO-RBF优化的新型自适应滑模控制器Fig. 2 New adaptive sliding mode controller based on PSO-RBF optimization

(26)

式中:FA、FB、FC、FU、FV、FW分别为A、B、C、U、V、W六相瞬时磁动势;Fm为基波磁动势幅值;θ为电机电角度。

得到SPPMSM正常运行时合成磁动势为:

∑F=iA+iBej120°+iCe-j120°+iUej30°+

iVej150°+iWe-j90°=3Fmejθ

(27)

当SPPMSM正常运行时,注入定子绕组的为对称正弦电流,各相生成的磁动势中负序分量会相互抵消,只留下正序分量,产生圆形合成磁动势轨迹。

SPPMSM的A相出现断相故障时,iA=0,六相电机变为五相不对称结构,绕组分布如图3。此时,剩余五相健康相合成磁动势可分解为两个幅值有差别旋转方向相反的磁动势,导致剩余健康相合成磁动势轨迹转变为椭圆形。

此时只要式(27)成立,就可以使得故障前后定子合成总磁势不变。实际上,每相电流可由式(28)表示:

ir=arImcosθ+brImsinθ

(28)

式中:r=A,B,C,U,V,W。

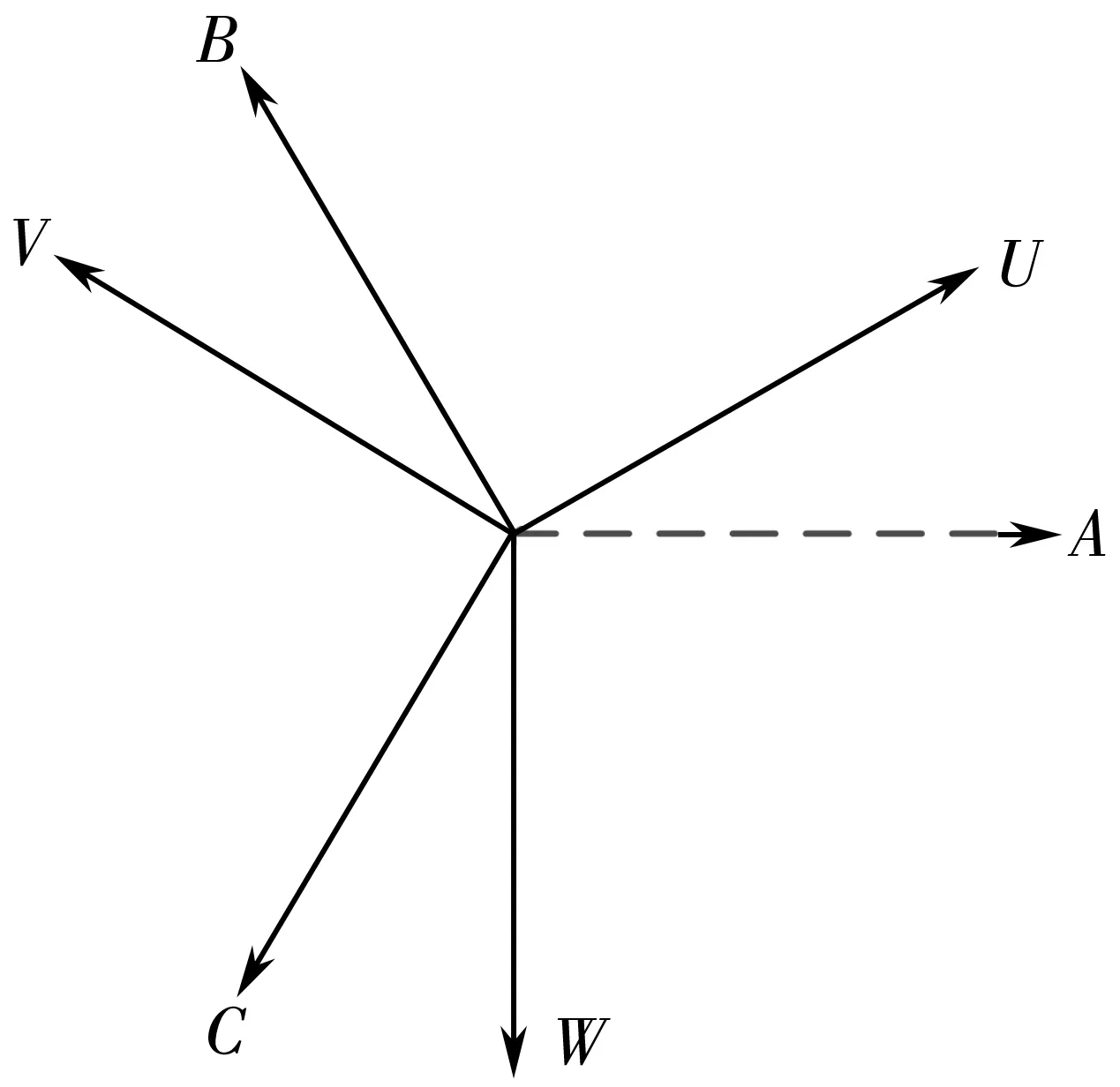
图3 A相断相故障下船舶推进电机绕组分布Fig. 3 Winding distribution diagram of marine propulsion motor under phase A phase failure

将ar和br作为待求量,根据式(27)与式(28)可得:

(29)

当两套绕组的中性点通过中线连接时,各相电流之和恒为零,如式(30):

(30)

为了保证故障后剩余绕组之间的电流相互平衡,即缺相后剩余各相电流幅值相等,如式(31):

(31)

SPPMSM在缺相故障运行时,为保证输出转矩平稳,各相定子电流的幅值会随之增大,这样定子铜耗会随着电流的增大而增大,这对于船舶十分不利。故笔者以定子铜耗最小为目标,其可以转换为求取各健康相定子电流幅值的最小平方和f,有:

(32)

可得到缺相故障下基于定子磁势补偿的剩余相电流为:

3 新型自适应滑模容错控制系统

SPPMSM容错控制框如图4,其中包括一个转速环SMC调节器和4个电流环PI调节器。

这种控制方法可以将对SPPMSM的控制等效为对两台三相PMSM的控制,且两套系统均采用id=0的控制策略。当iq1=iq2时可保证两套绕组输出电流幅值相等且均为正弦,从而保证输出功率一致。

由PSO-RBF优化的自适应滑模控制器作为转速环的控制器,由PI控制器作为电流环的控制器在断路故障发生后通过对剩余健康相电流进行补偿,以此达到推进电机容错控制的效果,从而实现推进电机容错控制。

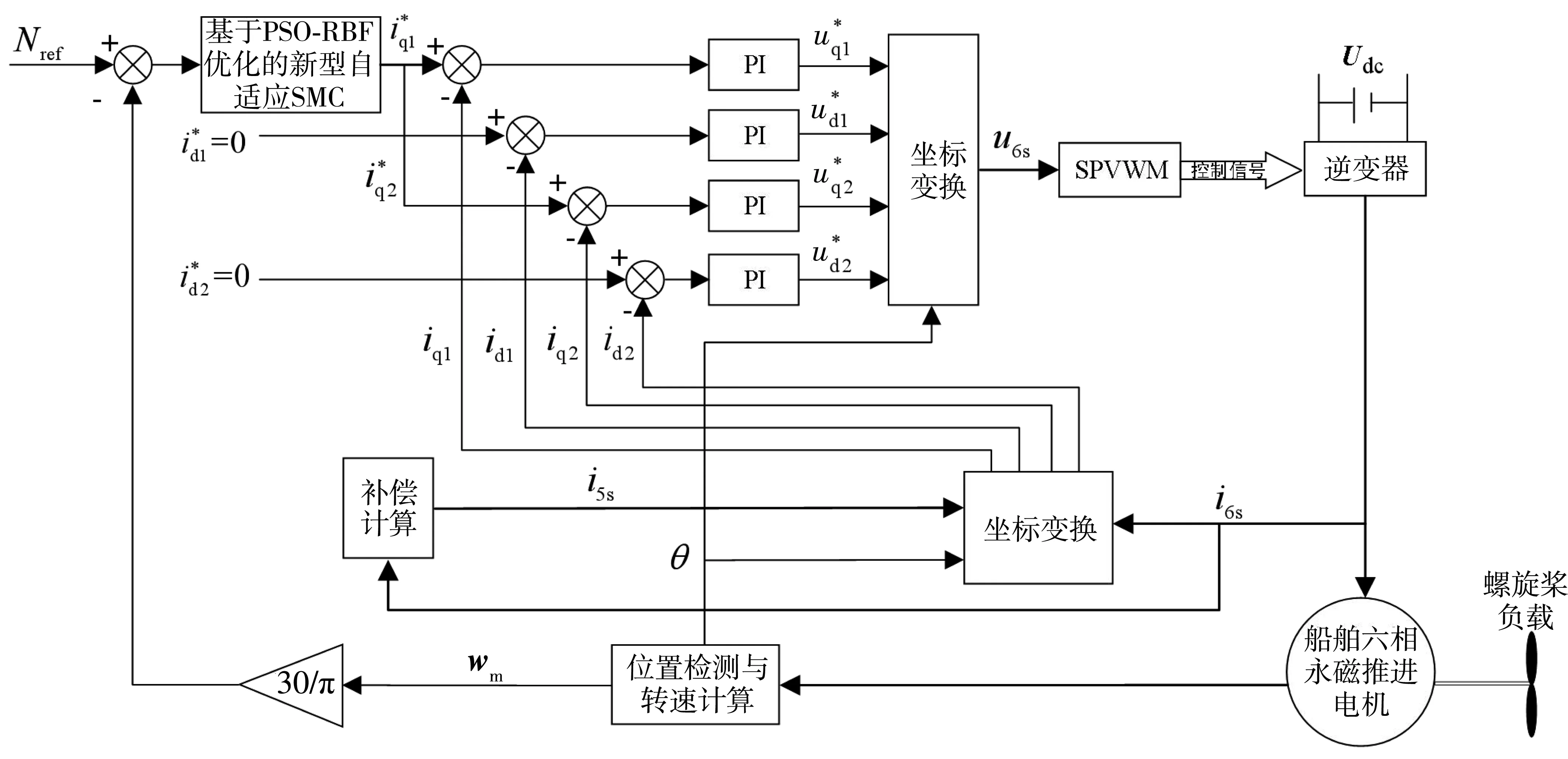
图4 船舶六相推进电机容错控制框Fig. 4 Fault-tolerant control block diagram of ship six phase propulsion motor

以某小型渔船电力推进系统为研究对象,船舶六相推进电机模型参数如表1,在MATLAB/Simulink仿真环境下,分析船舶在进出港、海上全航速工况以及螺旋桨负载突加、减情况下的系统控制性能。

仿真试验中电机运行时间小于实际电机运行时间,但这对于船舶推进电机控制算法的性能验证没有影响。定义正常运行时螺旋桨转矩为400 N·m,将传统SMC、新型SMC以及基于PSO-RBF优化的新型SMC 3种控制策略下的结果进行比对。

仿真中定义80 r/min为港内全速,120 r/min为海上全速,滑模转速控制器参数设置为c=3.5,q=1 500,μ=2,σ=0.05,电流环PI控制器参数KP=9.6,KI=1 680,采样时间均为10-5s。

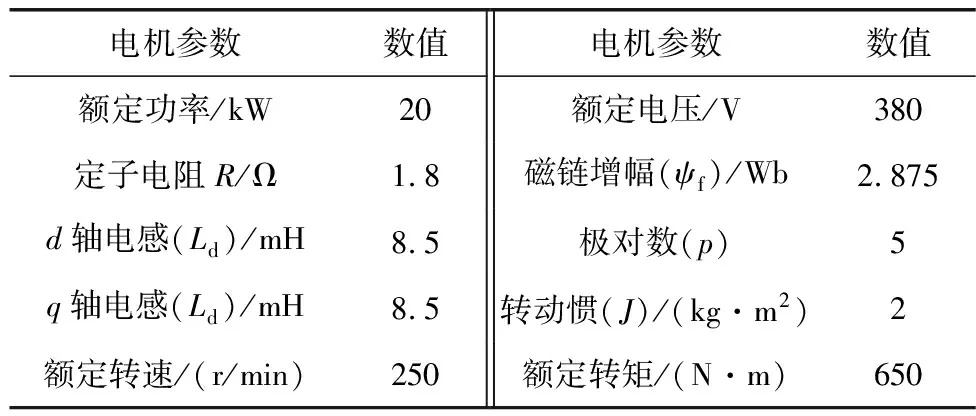
表1 船舶六相推进电机仿真参数Table 1 Simulation parameters of ship six phase propulsion motor

3.1 推进系统加减速及突加减负载仿真

为验证控制系统性能,进行如下仿真:

初始阶段船舶在港内启动至全速,推进电机转速在1.3 s时稳定至80 r/min,转矩稳定至400 N·m;3.5 s时船舶出港随后加速到海上全速,推进电机转速在4.8 s时稳定至120 r/min;7 s时在海上受到风浪影响螺旋桨部分出水,导致转矩骤降至200 N·m;9.0 s时恢复正常,推进电机在10.1 s时恢复稳定;12 s时准备进港,推进电机在14 s时减速至80 r/min;15.0 s时螺旋桨被异物缠绕导致转矩骤增至600 N·m,推进电机在16.0 s时恢复稳定;18.0 s时转矩恢复至400 N·m,直至20.0 s仿真结束。仿真期间推进电机转速、转矩变化曲线如图5。

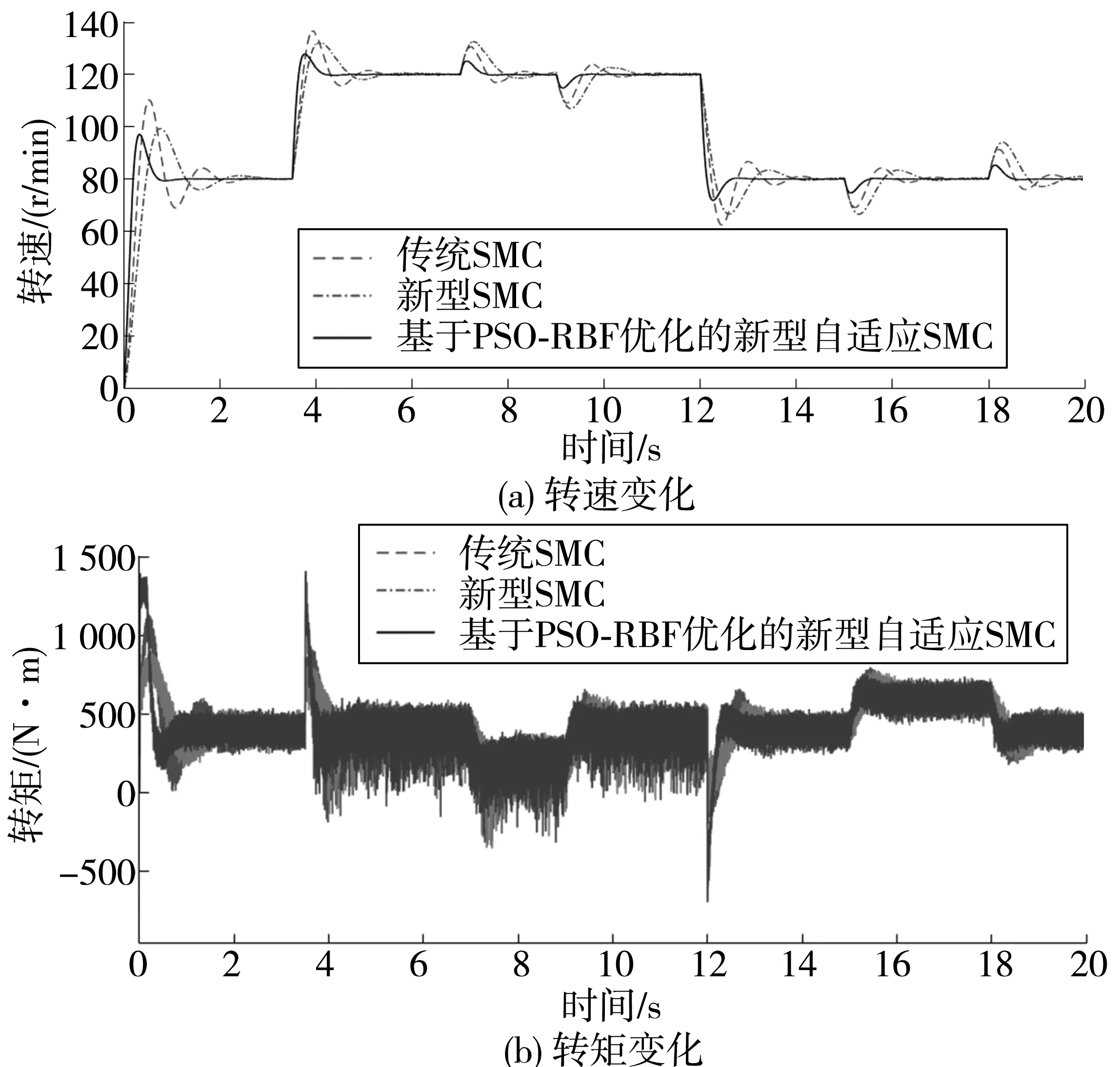
图5 三种控制策略下船舶推进电机仿真结果Fig. 5 Simulation results of ship propulsion motor under three kinds of control strategies

由图5可知:基于PSO-RBF优化的新型自适应滑模控制器的控制效果,明显优于传统滑模控制器和新型滑模控制器。在面对船舶加减速以及负载突变的情况下,笔者提出的新型控制策略调节速度快,转速脉动也明显低于其余两种控制策略,可以预想基于PSO-RBF优化的新型自适应滑模控制下的船舶推进电机在正常航行及面对突发情况时将有更好性能。

3.2 缺相故障容错仿真

仿真条件为:舶推进电机带螺旋桨负载启动且稳定运行,转速稳定至120 r/min,转矩稳定至400 N·m;3.0 s时推进电机A相发生断路故障,随后容错控制开始。基于PSO-RBF优化的新型自适应滑模容错控制策略下的船舶推进电机电流如图6。

由图6可知:A相发生断路故障时,故障相电流ia降为0,B相和C相两健康相电流相位互差180°。在容错控制策略的作用下,剩余五健康相电流从故障前的40 A增至55 A,约为原先电流幅值的1.3倍,与之前分析结果一致。

在3种控制策略下的船舶推进电机控制性能对比如图7。

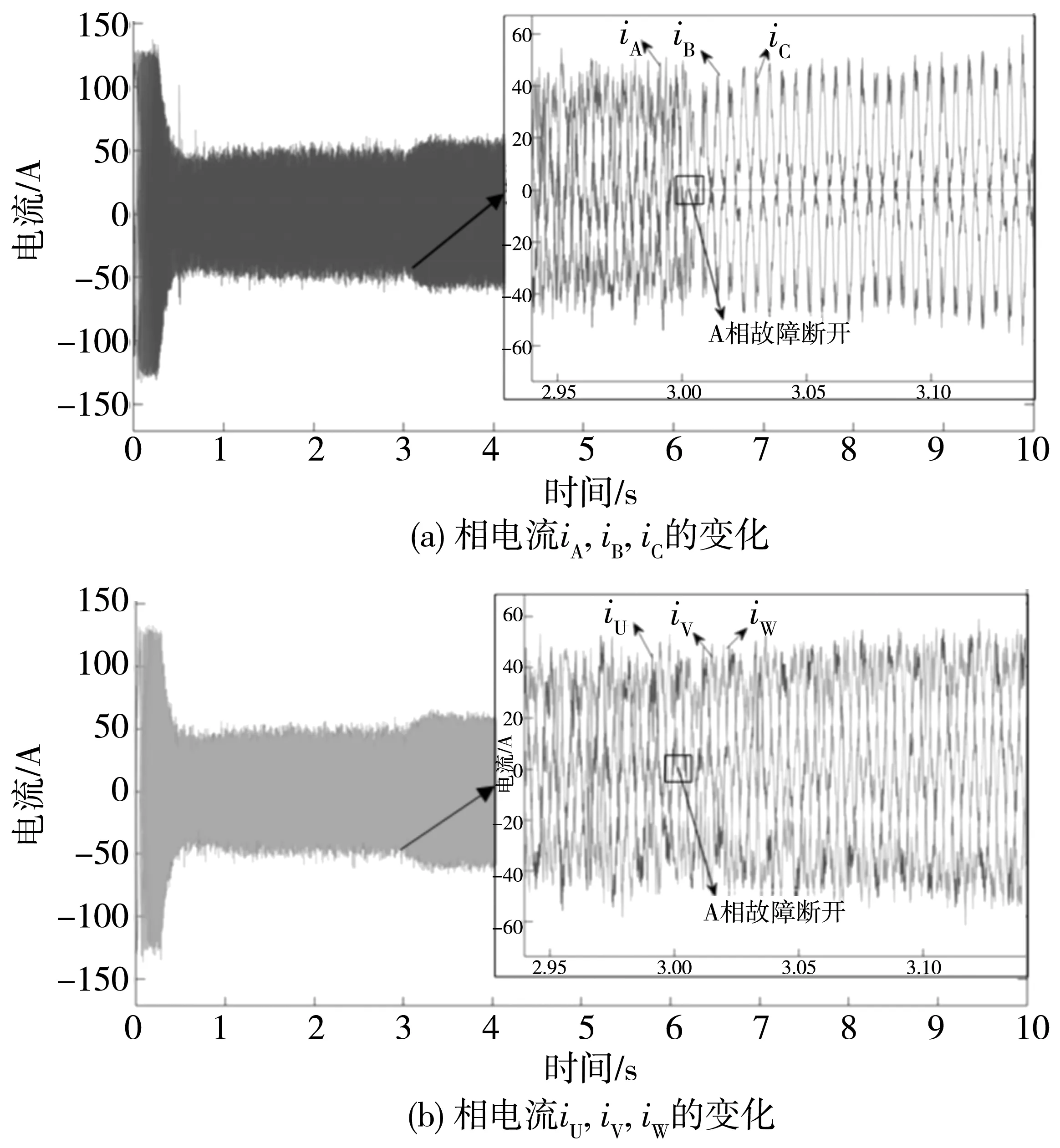
图6 基于PSO-RBF优化的新型自适应滑模容错 控制策略下的船舶推进电机定子电流Fig. 6 Stator current diagram of marine propulsion motor under a new adaptive sliding mode fault-tolerant control strategy based on PSO-RBF optimization

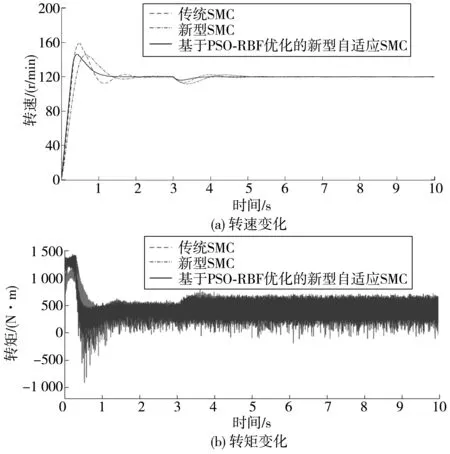
图7 3种控制策略下船舶推进电机控制性能对比Fig. 7 Comparison of control performance of marine propulsion motor under three kinds of control strategies

由图7可知:故障发生后,船舶推进电机转速及电磁转矩出现较大波动,随后立即进行容错控制,基于PSO-RBF优化的新型自适应SMC使得调节时间相较于传统的滑模控制缩短了1.7 s,且转速脉动更小,推进电机能够更加平稳地运行。但由于出现故障,导致系统控制性能下降,3种控制方法的转矩脉动会增大,3种控制策略性能比较如表2。

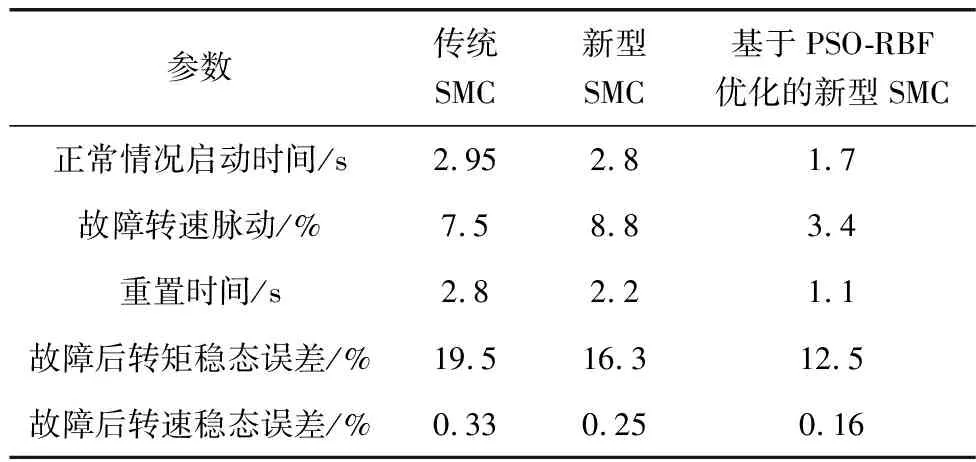
表2 3种控制策略性能对比表Table 2 Performance comparison of three kinds of control strategies

由表2可知:采用笔者提出的新型容错控制策略,船舶推进电机的输出转矩更加稳定,可获得更加稳定的转速控制性能。

提出的基于PSO-RBF优化的新型自适应滑模控制器可以在船舶推进电机出现单相缺相故障时,使转速更快恢复到额定转速,并让船舶推进电机转矩稳态误差更小,具有较强的容错性。

4 结 论

以船舶六相永磁同步推进电机为研究对象,综合分析了推进电机故障前后的定子磁势不变的控制策略,提出了一种基于PSO-RBF优化的缺相故障新型自适应滑模容错控制策略。实验结果表明:

1)提出的新型控制策略在船舶推进电机正常运行状态下,面对船舶加减速以及突加突减负载等工况时,在转速稳态精度和转矩响应速度上较传统滑模控制有明显改进。

2)根据推进电机断相前后磁动势不变原理,通过对剩余健康相电流进行补偿,配合PSO-RBF自适应滑模控制器,在推进电机出现缺相故障后,相比传统的滑模控制,转速脉动变小,转速稳态误差和转矩稳态误差均有所减小,推进转速恢复正常更快,具有较强的容错能力。