基于菲克第二定律的再生沥青中新旧沥青扩散融合研究

田小革,姚世林,卢雪蓉,窦文利,昶慧芹

(1. 长沙理工大学 交通运输工程学院,湖南 长沙 410114; 2. 河北省高速公路京雄筹建处, 河北 保定 071700; 3. 承德市交通局交通规划设计院,河北 承德 067000)

0 引 言

在低碳环保观念的逐渐深入和石油等不可再生能源逐渐匮乏的时代背景下,如何充分、有效地对废旧沥青混合料进行再生利用已经迫在眉睫[1-3]。

目前,已有学者从宏观或微观角度对新旧沥青间的融合状态进行了少量研究。 ZHOU Peili等[4]利用Material Studio软件,基于沥青的四组分建立相应模型,并以扩散系数作为融合评价指标,结果表明,扩散模型在20 ps后趋于稳定且扩散程度随温度升高而增大;S. VASSAUX等[5]使用红外成像显微镜,以羰基函数的空间分布定义了融合程度,研究了温度和时间对老化沥青混溶程度的影响;高飞[6]采用扩散定律数学表达式并结合Crank单向扩散模型对新旧沥青的扩散过程进行研究,结果发现,新旧沥青间的扩散可以采用菲克第二定律进行描述;林怡婧等[7]、陈龙等[8]采用分子动力学从分子尺度构建新旧沥青混溶模型,在微观尺度模拟了新旧沥青混溶过程,同时分析计算了再生沥青的宏观物理性能;石鹏程等[9]、郭鹏等[10-11]利用红外光谱分析仪(FTIR)和原子力显微镜(AFM)对再生沥青中新旧沥青的扩散融合进行了试验研究,结果显示,羰基指数和亚砜基指数与再生沥青中的新沥青掺量呈现相反规律。

目前,针对新旧沥青界面扩散融合行为的评价研究主要聚焦在利用不同混合模型和不同扩散理论从微观或宏观的角度定性或定量分析,而针对新旧沥青界面扩散融合程度所产生的内部性质变化(模量、官能团、组分等)以及温度和时间的变化对新旧沥青的扩散行为还需要进一步研究。

针对上述问题,笔者采用新旧双层沥青试样,通过动态剪切流变试验,结合菲克第二定律给出适合新旧沥青混溶体系的扩散模型;利用再生沥青中新旧沥青占比不同对应其复数剪切模量值不同的特性,以新-旧沥青混合体系的复数剪切模量G*值作为性能变化的表征参数,研究不同扩散时间、不同扩散温度下的再生沥青的扩散规律;最后采用双因素方差分析法评价时间、温度对扩散融合的显著性。该项研究有利于掌握再生沥青中新旧沥青扩散特性, 提高旧沥青的再生程度,促进沥青再生体系的完善。

1 新旧沥青扩散融合试验

1.1 老化沥青的制备

选用东莞泰和沥青产品有限公司生产的埃索(Esso)70# 以及90# A级道路石油沥青为基质沥青,其性能指标分别见表1。根据JTG E20—2011《公路工程沥青及沥青混合料试验规程》,先利用旋转薄膜烘箱对基质沥青进行短期老化,老化条件为在163 ℃保持85 min;然后再采用PR9-300压力老化仪(PAV)进行长期老化,老化条件为封闭加压至2.1±0.1 MPa,在100 ℃下老化20 h。

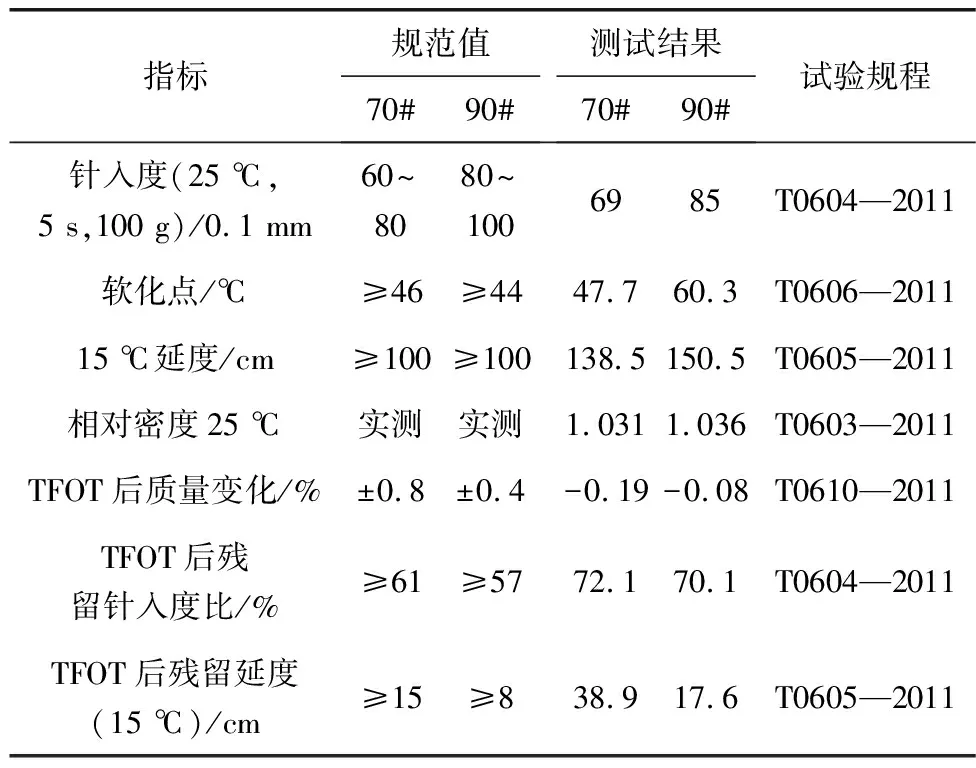
表1 埃索 -70# &90# 基质沥青的性能指标Table 1 Performance index of Esso-70# &90# base asphalt

1.2 基于菲克第二扩散定律的计算模型

笔者采用菲克第二定律对再生沥青的扩散融合行为进行计算和研究,见式(1):

(1)

式中:c为新沥青浓度;t为扩散时间;r为扩散位置;D为扩散系数。

1.2.1 计算模型

笔者采用直径为25 mm,厚度为2 mm的老化沥青与新沥青双层沥青试样。新沥青在上,旧沥青在下,新沥青均匀分布在旧沥青的表面,且新、旧沥青层厚度相同。将再生沥青任意划分为等厚度的子层,模拟再生沥青混合料表面新旧沥青的扩散融合,如图1。

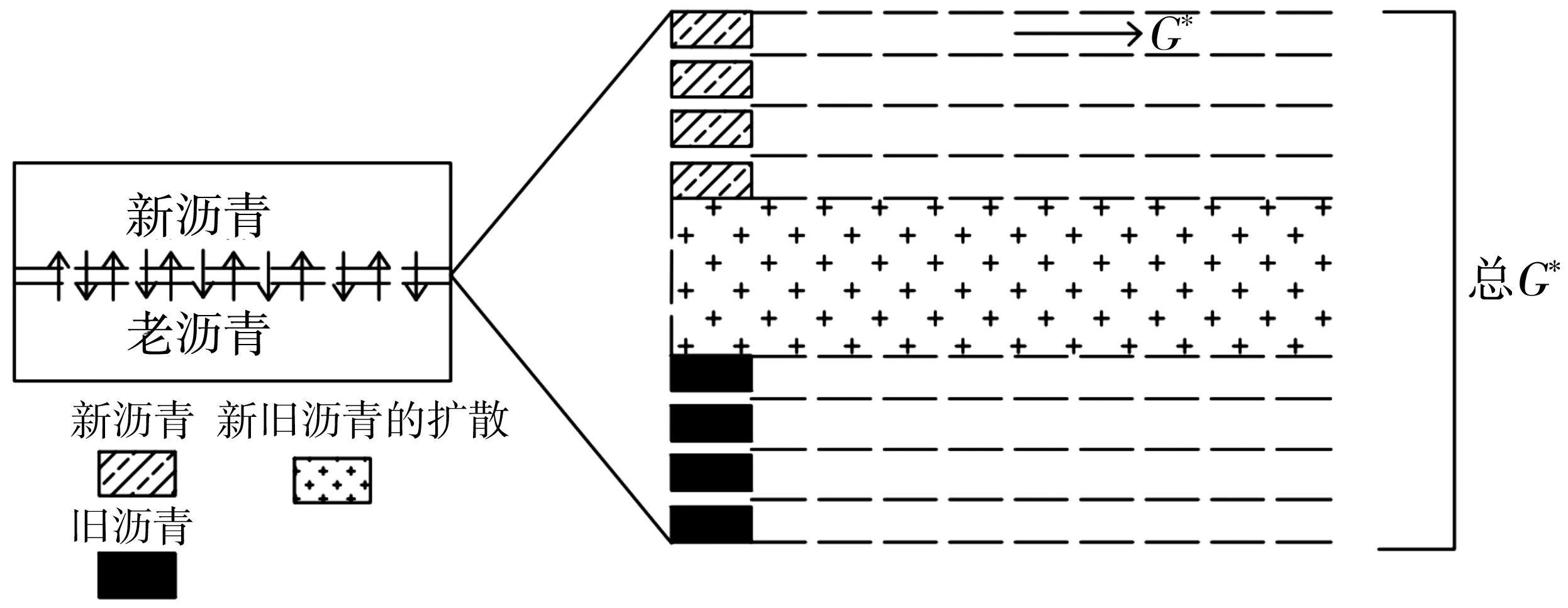
图1 新-旧沥青双层沥青试样模型Fig. 1 Model of new-old asphalt double-layer asphalt specimen

1.2.2 初始条件

在初始时刻,认为新沥青层各处的浓度均匀分布且相等,旧沥青层中新沥青的质量分数定义为0,而新沥青层中新沥青的质量分数定义为c0,取c0=1,如式(2):

(2)

式中:r1为骨料半径;r2为旧沥青层到骨料中心半径;r3为新沥青层到骨料中心半径;初始时刻取c0=1。

1.2.3 边界条件

在旧沥青与骨料界面处,规定新沥青的扩散通量为0,如式(3):

(3)

式中:t为扩散时间。

1.2.4 新沥青在旧沥青中扩散过程的理论解

笔者将旧沥青划分为n层,结合计算模型与初始条件、边界条件,根据学者们的研究推导[6],各分层中的新沥青浓度可根据菲克第二定律得出,其中新沥青在旧沥青层中的质量分数(即浓度)如式(4):

(4)

式中:C(r,t)为扩散时间t时,距离骨料与旧沥青表面r1处新沥青的浓度;D为扩散通量,又称扩散系数;r3-r1为扩散总层厚,取r3-r1=2 mm;n为双层沥青试样被划分的层数,取n=10;r为再生沥青各层距旧沥青与骨料的接触面r1处的距离。

1.2.5 计算思路

(5)

式中:a、b、c为拟合参数;x为新沥青浓度。

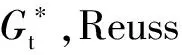
(6)

式中:T为总沥青层厚度,T=2 mm;h1,h2,h3,…,hn分别为每个分层的厚度;G1,G2,G3,…,Gn分别为每个分层的复数剪切模量。

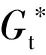
1.3 试验思路与步骤

复数剪切模量G*值易于测试且敏感性较强,因此笔者采用新-旧沥青混合体系的G*值作为再生沥青性能变化规律的评价指标,并以此为基础研究新旧沥青扩散融合规律。笔者定制了直径为25 mm,槽深为1 mm以及直径为25 mm,槽深为2 mm的耐高温硅胶模型,利用该模型实现新旧沥青在不同条件下分子扩散,以此来模拟菲克第二定律下再生沥青混合料中新旧沥青的扩散融合过程,步骤如下:

1)利用前期经过短期和长期老化的70# 老化沥青与90# 老化沥青,将老化沥青和同等级的新沥青加热至流动状态与玻璃注射器一起放入烘箱中备用。

2)在旧沥青中加入相同等级的新沥青,将其搅拌均匀,以25%为浓度梯度改变新沥青占新-旧沥青总质量的百分数(0%,25%,50%,75%,100%)。等再生沥青冷却至常温后,采用MCR301型动态剪切流变仪(转动轴直径为25 mm,试验频率选定10 rad/s,底板与转动轴板之间的间距调为1 mm,应力设为2%)对两种不同新沥青掺量的70# 再生沥青与90# 再生沥青进行动态剪切流变试验 (64 ℃温度下),测其复数剪切模量,得到回归方程。

3)将槽深为1 mm的硅胶模型放置平稳,并用玻璃注射器向一组硅胶模型槽中缓慢注射一定质量的新沥青,在另一组硅胶模型中注入旧沥青,注意注入沥青不能超过槽深,沥青液面需平整,室温冷却后将新、旧沥青试样放入槽深为2 mm的硅胶模型中,旧沥青试样在下,新沥青试样在上。

4)将装有新-旧沥青双层试样模型的槽深为2 mm的硅胶模型平稳放置在烘箱中,分别在80、100、120、140 ℃的烘箱内分别保温不同时间(10、20、30、60、90、120 min)后取出,为立即停止新、旧沥青的扩散,将硅胶模型放入冰箱中冷冻15 min。

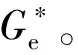
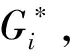
2 基于菲克定律的新旧沥青间扩散融合

2.1 不同新沥青掺量下的再生沥青复数剪切模量

不同新沥青掺量的再生沥青G*值变化规律如图2。根据图2可以发现,70# 再生沥青的G*均大于90# 沥青G*值,且变化趋势一致,这可能是因为在相同温度下90# 沥青更加容易扩散。两种再生沥青的复数剪切模量与新沥青掺量的线性回归方程精度分别为0.990、0.988,拟合精度较高。为计算出含有任意比例新沥青的双层新旧沥青模型的总复数剪切模量G*,试验选择将复数剪切模量与新沥青掺量进行线性回归,其中70# 再生沥青如式(7)、90# 再生沥青如式(8):

G*=15.469e-0.018 9x-0.735 1

(7)

G*=11.547e-0.0204x-0.097 9

(8)

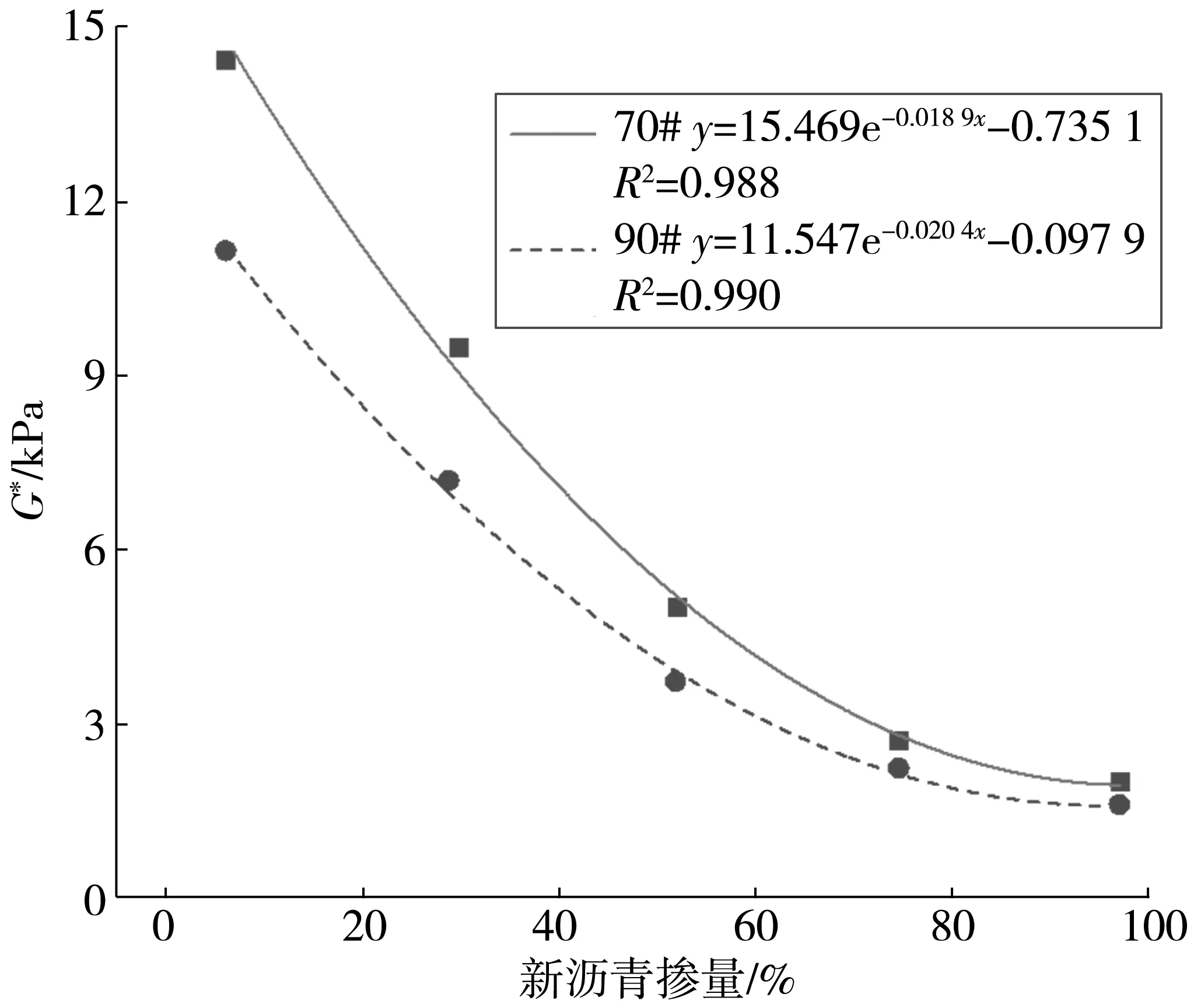
图2 不同新沥青掺量的再生沥青G*值变化规律Fig. 2 Change laws of the G* value of recycled asphalt with different new asphalt contents

2.2 再生沥青中新旧沥青间的扩散试验结果与分析

根据计算思路中式(5)和式(6)的相关方法得到不同扩散温度(80、100、120、140 ℃)、扩散时间下(10、20、30、60、90、120 min)70# 与90# 再生沥青的理论值与实际值,如图3、图4;将理论值与实际值取其平均探究温度对不同种类再生沥青复数剪切模量的影响,如图5。

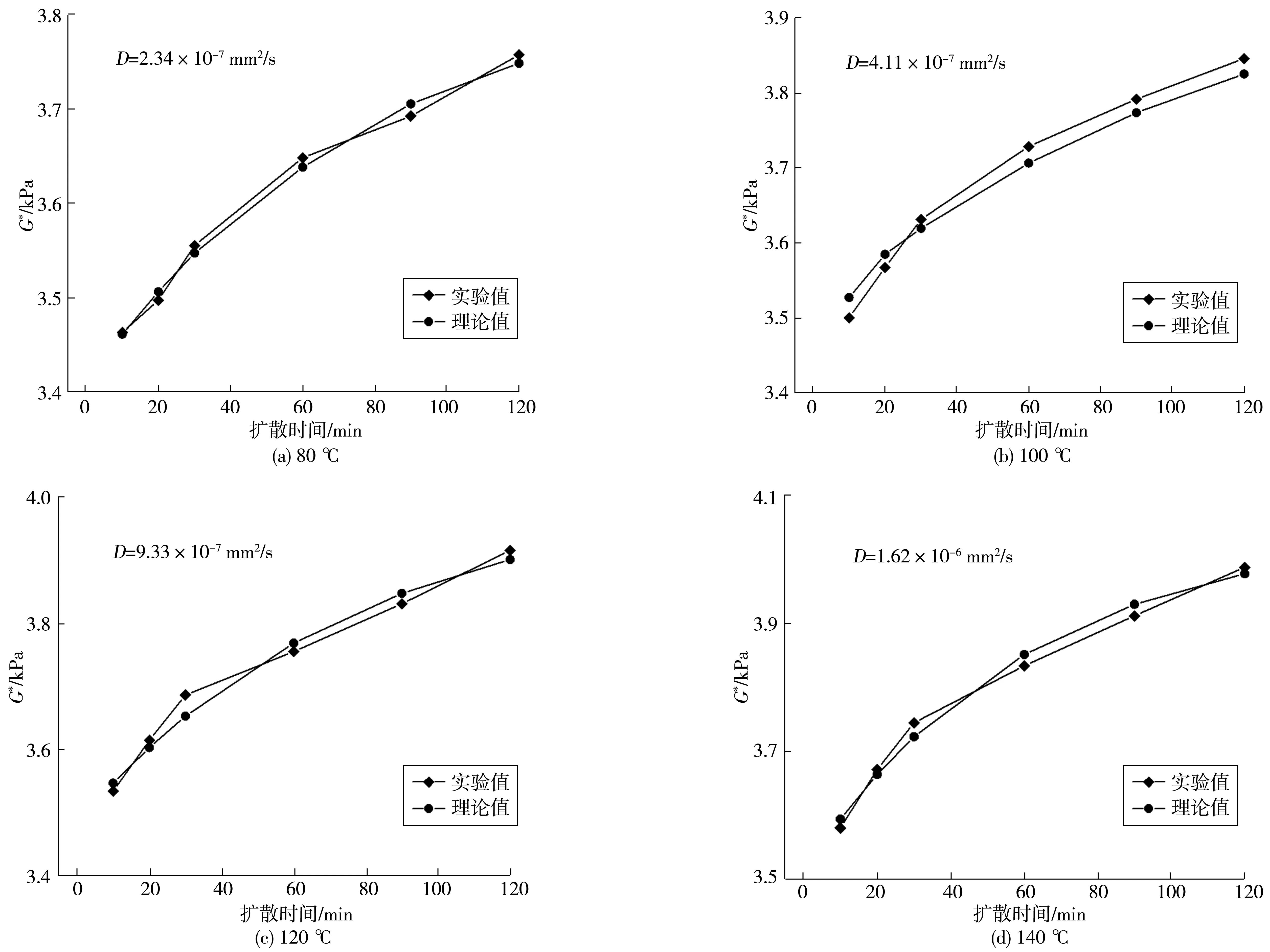
图3 不同扩散时间下70# 再生沥青的理论值与实际值Fig. 3 Theoretical and actual values of 70# recycled asphalt at different diffusion times

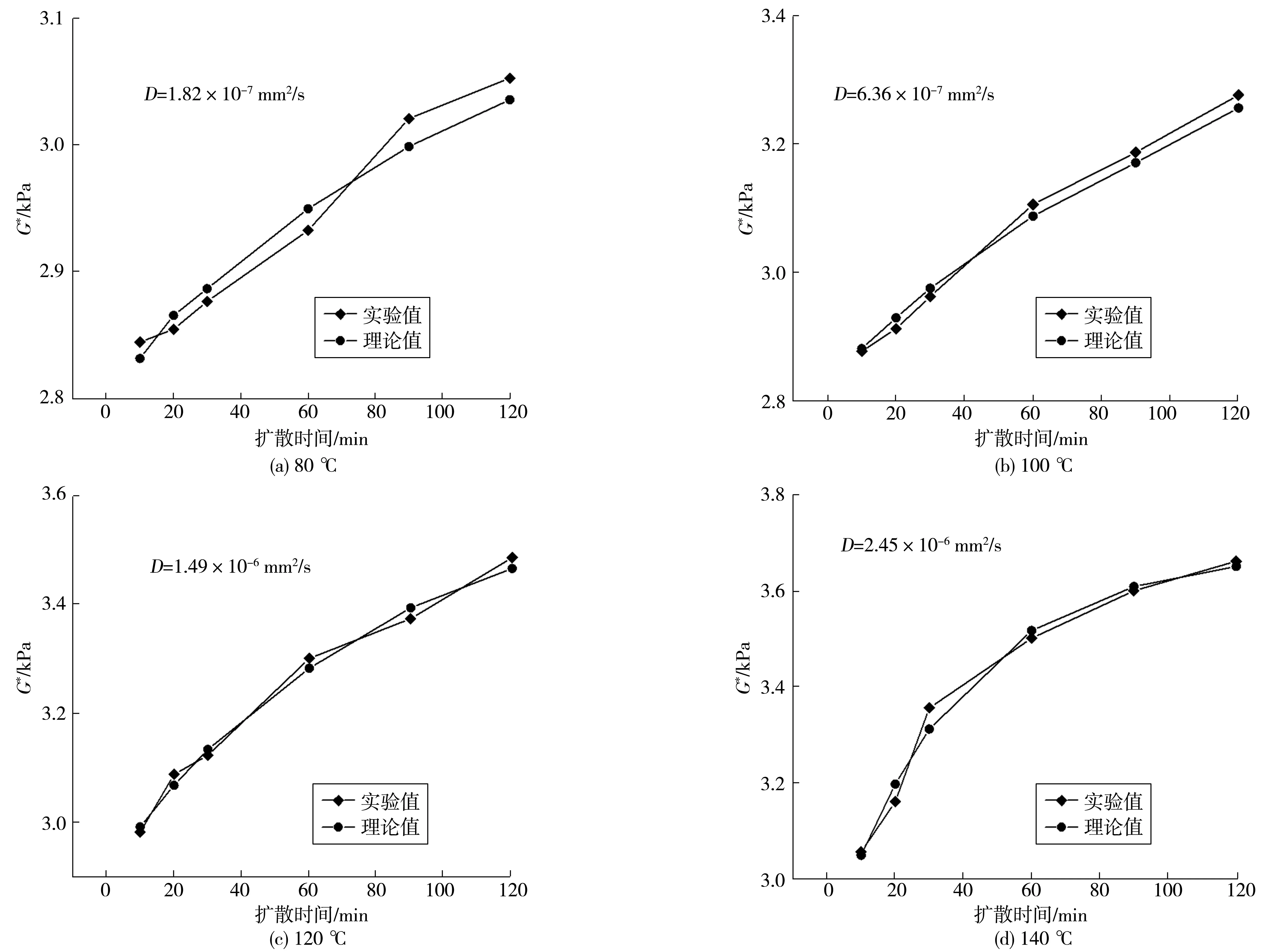
图4 不同扩散时间下90# 再生沥青的理论值与实际值Fig. 4 Theoretical and actual values of 90# recycled asphalt at different diffusion times

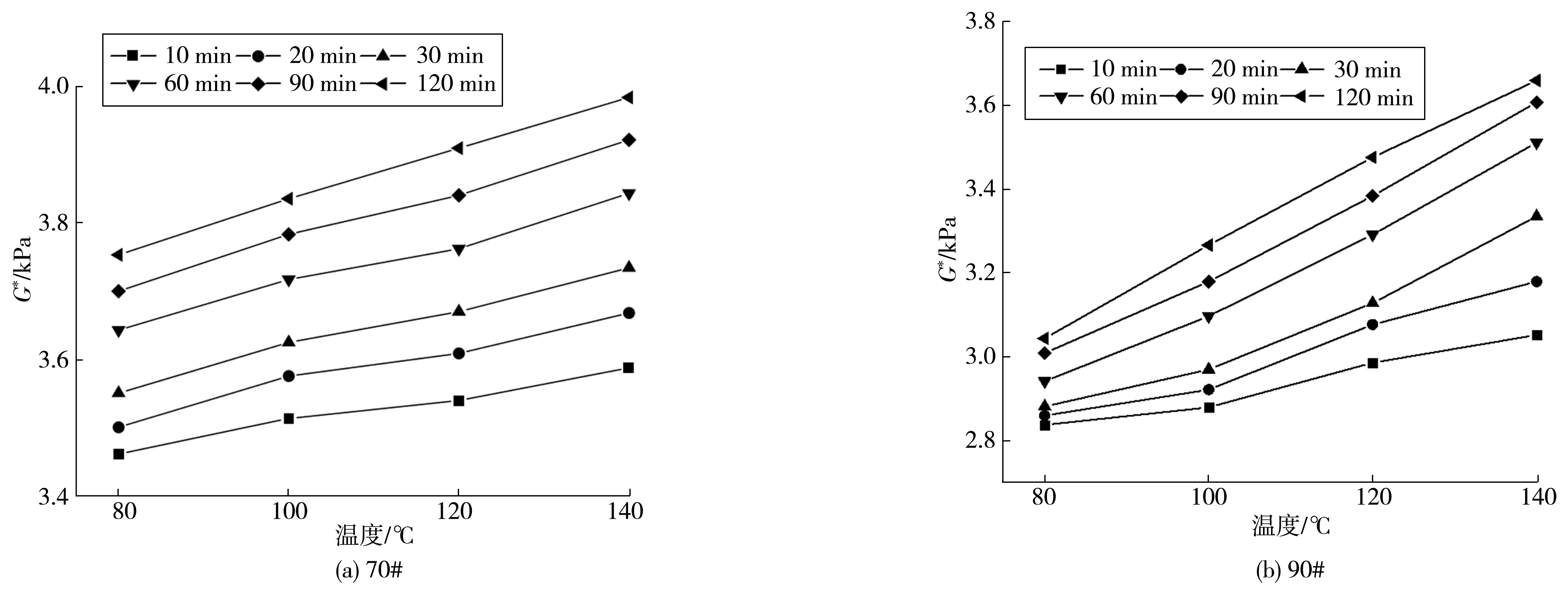
图5 不同温度下再生沥青的复数剪切模量Fig. 5 Complex shear modulus of recycled asphalt at different temperatures

由图3～图5可以发现:

1)采用菲克定律以及混合体系的Reuss模型对再生沥青的扩散现象进行描述,对于确定的扩散系数D,再生沥青复数剪切模量的试验值与理论值具有很好的吻合效果,所以新-旧沥青间的扩散融合规律可以采用菲克第二定律进行描述。

2)随着扩散时间、扩散温度的增加,不同种类再生沥青试样的G*值逐渐增大。这是因为在层间界面位置处,新、旧沥青分子在高温和时间的作用下发生了扩散融合,新沥青分子不断扩散渗透入老化沥青中,使前者弹性成分逐渐增大。

3)当扩散温度为80～100 ℃时,两种再生沥青的复数剪切模量在前30 min增长幅度缓慢,后90 min增长幅度变大,扩散速度加快,这说明温度较低时,新旧沥青之间一开始也会发生扩散现象,只是扩散现象缓慢,随时间的延长,扩散现象逐渐加快。当温度提高至120～140 ℃ 时,两种再生沥青的复数剪切模量随时间的延长呈指数形式增长,其增长率在前60 min均比后60 min要大。这是因为在高温条件下,沥青可以得到充分软化,其流动性逐渐增强,分子运动剧烈,扩散现象明显,随着新沥青逐渐扩散进入旧沥青中,其浓度差逐渐减小,界面分子扩散驱动力逐渐不足,因此扩散现象逐渐减弱。

2.3 扩散时间、温度对再生沥青扩散系数的影响

排除试验误差和畸点,再生沥青的复数剪切模量G*试验值与根据菲克第二定律计算得到的理论值具有较高的吻合度,其扩散系数如图6。

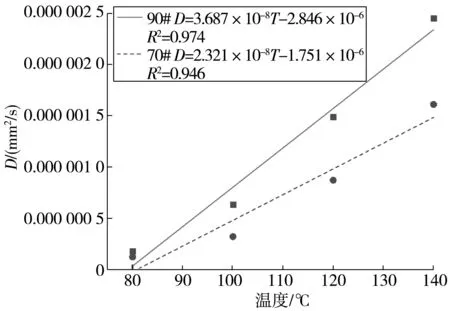
图6 两种再生沥青在不同温度下的扩散系数Fig. 6 Diffusion coefficients of two types of recycled asphalt at different temperatures

由图6可以发现:

1)当温度每上升20 ℃,70# 再生沥青的扩散系数大约上升2倍左右,而90# 再生沥青的扩散系数大约上升2～3倍左右。由此可看出,在旧沥青中添加与其相同等级基质沥青的扩散组合受温度影响的敏感性程度不同。此外,扩散温度对新旧沥青界面处的扩散融合作用显著,且温度的增加对新旧沥青扩散系数的影响比较平均。

2)当温度为80～140 ℃时,90# 再生沥青的扩散系数大于70# 再生沥青,这是因为在高温条件下,90# 再生沥青比70# 再生沥青更容易软化,呈流动状态,而沥青分子的运动遵循布朗运动,温度越高,分子运动越剧烈,扩散系数也越大。此外,沥青作为一种黏弹性材料,随着温度的升高,新、旧沥青的黏滞性降低,分子间的作用力减小,有利于扩散系数的增加。

3)不同标号的沥青对再生沥青的扩散融合程度影响不同。随着扩散温度的上升,两种再生沥青的扩散系数不断增长,90# 和70# 再生沥青的扩散系数均呈线性模式增长,其线性回归方程的拟合精度分别为0.974、0.946,90# 再生沥青斜率明显大于70#,说明在相同温度条件下90# 再生沥青扩散融合程度更好。

2.4 扩散时间、温度对不同再生沥青扩散规律的因素敏感性分析

利用IBM SPSS Statistics 26软件对两种再生沥青进行扩散时间、扩散温度的敏感性分析,主体间效应检验(因变量为复数剪切模量)结果如表2。

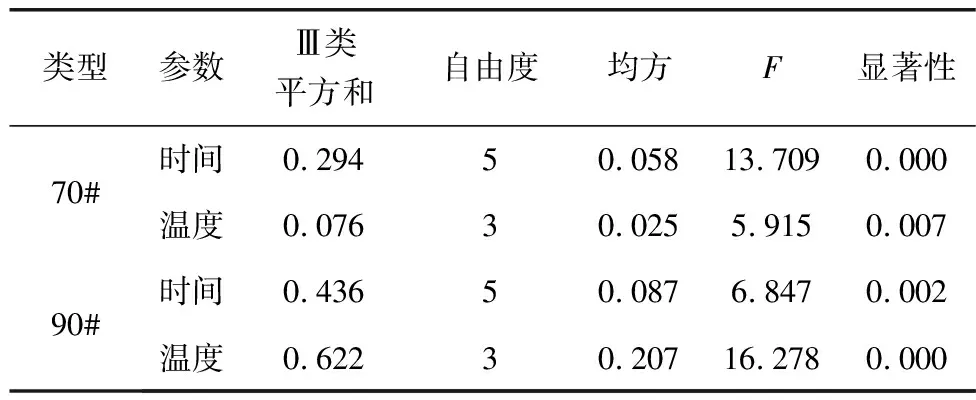
表2 再生沥青扩散结果方差分析Table 2 Analysis of variance of diffusion results of recycled asphalt

由表2可以发现:

1)扩散时间与扩散温度对两种再生沥青的扩散融合作用均有显著影响。这是因为无论是70# 沥青还是90# 沥青都会随着温度升高,先软化呈流动状态,温度越高,分子运动也会更加剧烈,扩散作用越明显。相同的,随着时间的延长,沥青可以得到充分软化,分子间的运动也会随着时间的延长而增加作用次数,从而提高沥青间的扩散融合。

2)对于70# 沥青的扩散效应,时间的影响更大,而对于90# 沥青的扩散效应,温度的影响更大。这是因为70# 沥青的高温稳定性高于90# 沥青,90# 再生沥青的软化点较低,因此同等温度下,90# 再生沥青对温度更加敏感,温度增加降低了沥青的黏度,有利于分子间相互扩散,而温度升高,分子运动也会更加剧烈,从而促进新旧沥青间扩散融合。70# 再生沥青在同等温度作用下分子活跃程度低于90# 沥青,但随着时间的延长,新旧沥青扩散程度也会累加,而在高温条件下,随着时间的延长,新旧沥青可以得到充分软化呈流动状态,分子间的运动也会更加频繁。

3 结 论

通过动态剪切流变试验测定不同比例同等级基质沥青与旧沥青再生沥青的复数剪切模量,模拟新-旧沥青扩散融合过程,并采用菲克扩散第二定律对再生沥青的扩散融合过程进行数学计算,将根据动态剪切流变试验得到的试验数据与模拟数据进行对比,可以得到以下结论:

1)采用菲克第二定律以及混合体系的Reuss模型对再生沥青的扩散行为进行描述,结果表明,再生沥青复数剪切模量的试验值与理论值能很好地吻合,且扩散时间和扩散温度与不同种类的再生沥青试样动态复数剪切模量G*值成正相关。

2)再生沥青中新旧沥青扩散速率具有相同量级,为10-7左右,随着温度上升,90# 与70# 再生沥青的扩散系数均呈线性模式增长。不同老化沥青与基质沥青组成的扩散组合受时间、温度敏感性影响的程度不同。当温度较低时,70# 再生沥青的扩散系数比90# 大,而当温度逐渐升高时则相反。

3)采用无重复双因素方差分析法分析了扩散时间、扩散温度对再生沥青扩散融合的影响,结果表明,扩散时间、扩散温度均有显著影响。