深度学习：让数学学习走向深入

黄秋芳

［摘  要］ 在小学数学教学中，深度学习是促进学生思维进阶的有效途径。让学生基于课堂进行深度学习，能领悟和运用数学思想方法，开展合作交流，提升学习力和思维力。教师要以教学设计为支架，助力学生思维进阶，让数学学习走向深入。

［关键词］ 小学数学;  深度学习；思维进阶；教学设计

深度学习是一种基于建构主义理论的学习方式。北京师范大学郭华教授认为，深度学习就是在教师的引领下，学生围绕学习主题，全身心积极参与、体验成功、获得发展的有意义的学习过程［1］。在此基础上，笔者认为，在实际的数学教学中，深度学习体现在：教师立足于教学目标，基于教学设计，以问题为支架，让学生在知识建构和方法迁移中深化对知识的理解，进而促进其思维的发展。

一、问题引领：深度学习的立足点

小学数学看似简单，但是这简单背后需要教师深入地研读教材，教材研读是课堂教学的“根”。教师只有把教材“读厚”，正确到位地研读教材，课堂教学才不会偏离方向，才能更好地实现教学目标，构建高效课堂。

在教学设计中，驱动性问题是学生学习所指向的核心问题。深度学习视域下的数学学习鼓励学生提出问题，从学生的问题出发，既尊重他们的内在需求，又能生成课堂学习的焦点［2］。教师应以疑问为起点研读教材，触摸知识本质，感悟数学思想。同时教师应以学生的疑问为媒介，激发学生思维的积极性，引导学生去思考、探究、交流，使学生在探索数学问题的过程中能感受到学习数学的乐趣，促进学生思维品质的发展。

在教学“用方向和距离确定位置”时，简单的两页教材让学生产生很多疑问：在以前的学习中学生已经学习并认识了东北方向、东南方向等，为什么这一课要以北和南为基准来确定方向呢？为什么在确定位置的时候要确定方向（角度）和距离呢？在确定位置时一定要方向和距离同时存在吗？为了让学生真正理解，笔者对教材进行了再解读，并在教学过程中引导学生带着这些驱动性的问题进行了深入探讨。

教学片段：

师：本节课的课题是“用方向和距离确定位置”，为什么不能是用方向或距离确定位置？如果我们只知道距离，我们能确定的是什么？

通过教师引导学生进行思考讨论，学生从有争议到统一认识。

生：如果我们只确定距离，那我们能确定以观测点为圆心、以距离为半径的这个圆的范围。

师：如果我们只知道方向（角度）呢？

生：那么我们只知道那个具体的位置在一条射线上。

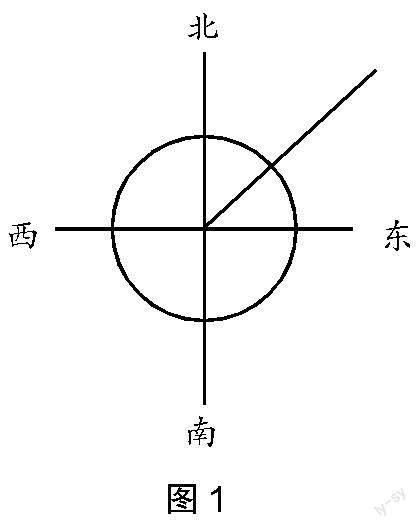
师：所以单独的方向或距离并不能确定具体的位置。那么当方向（角度）和距离同时存在时，二者相交的地方就是我们确定物体的位置（如图1）。

在这一探索的过程中，让学生带着疑问在问题的对比中经历探究的过程，能促进学生的深度理解。学生学会综合运用已有的知识理解确定位置几大要素的形成过程，体会数学中由“面”到“线”及“点”的本质，感受数学的严谨性，让数学知识的获得过程变得丰满而深刻，能促进思维深刻性和批判性的发展。

“为了理解而教”是哈佛大学的一句口号。理解是教育真正的核心目标，深度学习是为了培养学生的理解性思维，进而促进学生思维深刻性、批评性的发展。在学习过程中，学生通常习惯性接受教材的概念或者定义，教师要引导学生思考教材为什么会这样规定，让学生在追寻答案的过程中能一次次接近概念的本质。

二、表达交流：深度学习的有力支架

《义务教育数学课程标准（2022年版）》倡导：“学会用数学的语言表达现实世界。”［3］史宁中教授同样倡导学生学会数学地表达。可见数学表达在促进学生思维发展上的重要作用。学生的学习方式是多样的，在数学课上，教师需要给学生独立思考的空间和合作探究的机会，让他们在相互交流中促进自身数学表达和思考能力的提升。学生在合作探究的过程中，一方面通过交流、质疑、思辨能加深对知识的理解，实现深度学习；另一方面通过不同方法的交流，拓宽了学习的路径，促进了学生创造性思维的发展。

比如在学习了“圆的面积”的基础上，学生在学习“圆柱的体积”时能通过自主操作交流发现可以将圆柱转化成近似的长方体（如图2），进而根据圆柱和长方体之间的关系推导出圆柱體积的公式，即圆柱的体积：V=Sh。同时，通过操作，学生从另一个角度发现：圆柱的体积=侧面积的一半×半径。利用这一发现，学生就能够快速地解决不同类型的数学问题。

学生对于数学知识的学习，不能局限于对数学概念和数学公式的识记，这样思维会一直处于低阶的阶段。教师要激发学生无限的潜能，发挥学生的主观能动性，让学生在分析、综合、创造中发展空间观念，提升学生的核心素养，促进其高阶思维的发展。

新课程标准倡导教、学、评的一致性，这一主张从教学方法上改变了教、学、评的分离状态。因此，教师要为学生创造宽松的探索氛围，充分尊重学生的独特思维方式，培养学生善于分析、勤于思考的习惯。教师要鼓励学生在数学学习中学会交流、辨析、创造，让学生在思考中体会到探索、创造的乐趣，促进学生对数学知识的深度理解。

三、合作探究：深度学习的有效路径

合作探究是小学数学思维课堂的重要途径，课堂的合作探究不应流于形式，应以核心的问题为导向，让真问题成为学生理解问题、解决问题的脚手架，给予学生充分的空间与文本对话、与同伴对话，拓宽学生思维的广度和宽度，进而促进学生思维的进阶。

教学五年级下册“圆的面积”这一课时，教师通常利用教材给予的范例，让学生将圆平均分成若干等份拼成一个近似的长方形，经过操作交流发现：长方形的长等于圆周长的一半，长方形的宽等于圆的半径，因此推导出圆的面积公式是S=πr2。

学生已经学习了若干个平面图形，它们和圆能产生联系吗？教师不妨给予学生一个探索问题的空间，让学生借助学具创造出不同的方法来推导圆的面积公式。

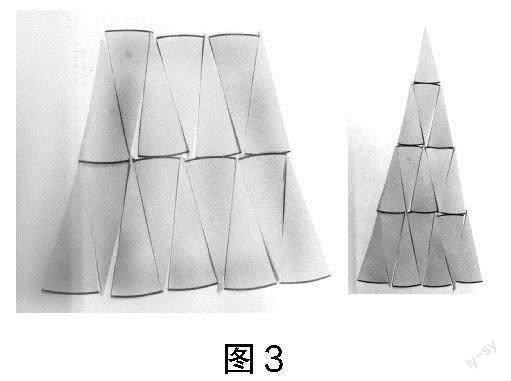
比如将圆平均分成16等份，可以拼成一个近似的梯形（如图3），梯形的上下底之和是圆周长的一半，即πr，高是2r，由梯形的面积公式S=（a+b）×h÷2，最终推导出圆的面积是S=πr2。这样，能让学生在问题的启发中、在实际的操作中体验、感悟和丰富圆的面积推导方法，进而在分析、综合、归纳中聚焦对圆的面积的理解。

在合作探究中，问题不仅能够激发学生的探究兴趣，而且导引着学生的探究行为。在课堂上，教师对问题的设置不能只局限于指向思维的记忆等低阶阶段，应结合具体的教学内容，引导学生能多角度、多侧面、多层次、多结构去思考、探究，在不同的呈现方式中抽象出事物的本质，促进发散性思维的发展［4］。

四、拓展延伸：深度学习的进阶生长

“问题解决”是数学学习、研究的最终指向所在。在数学教学中教师常常通过练习题的方式来进行思维的训练和检查学生的学习情况，但问题的解决不能等同于练习题。那么如何让学生在练习中既充满兴趣又能在挑战中促进思维进阶呢？这需要教师在遵循教学内容的梯度和学生的“最近发展区”的基础上，根据教学内容对练习题进行适当的拓展延伸。

在六年级上册“长方体和正方体”的练习题中，教师可以根据学生已有水平设计如下题目：“用1块长40厘米、宽20厘米的长方形硬纸片，做1个高为5厘米的无盖月饼盒（接缝处忽略不计），你有多少种设计方案？请画图表示，并算出这个纸盒的容积。”

这是一个开放性的题型，基于学生已有知识水平，学生能够探索出以下方法（如图4）：

（40-10）×（20-10）×5=30×10×5=1500（立方厘米）。

对于学有余力的学生来说，通过分析长方形的长和宽，能够从另一角度探索出第二种方法：将长中的20cm平均分成4份，将这4个长方形作为无盖月饼盒的两组对面（如图5）。

20×20×5=2000（立方厘米）。

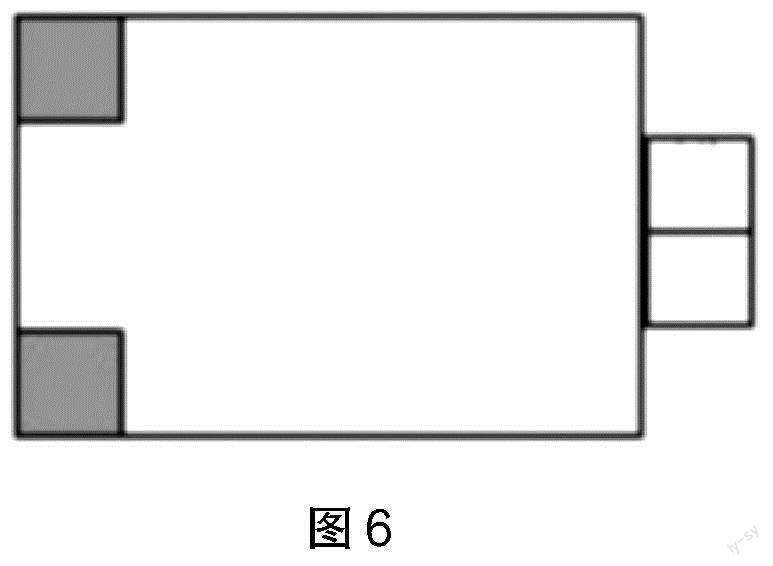
学生基于思维定式，很难发现第三种研究方法：即剪下两个边长为5cm的小正方形即可（如图6）。但在教师出示图形之后，学生经过观察、分析、讨论，能理解第三种表示方法的含义。

（40-5）×（20-10）×5=35×10×5=350×5=1750（立方厘米）。

《义务教育数学课程标准（2022年版）》中指出：“使得人人都能获得良好的数学教育，不同的人在数学上得到不同的发展。”［3］面对学生的疑问时，教师要善于以问题为媒介，用问题引导学生，让学生在已有知识的基础上，不断突破原有知识，挖掘简单数学问题下的方法的多样性。在教学设计中，这种练习题不仅能够深化学生对知识的理解程度，而且能够激发学生的学习兴趣，促进学生思维灵活性的發展。

五、回顾反思：深度学习的有效提升

回顾反思是学生在数学学习过程中应具备的重要能力。反思思维是理性思维，是深度思维，也是高阶思维。在数学学习中，有效的回顾反思不仅能深化学生对知识的理解，而且能促进其思维系统性的发展。

在复习三年级“年月日”这一单元时，由于知识点太过琐碎，学生在平常的复习中存在一定的难度。教师可以设计这样的问题，让学生在思考中回顾和系统地串联知识点。思考题：在班级里找出两位同学的生日（比如2008年10月5日、2009年3月6日），比较谁的年龄大，大多少天？

在活动中提出以下要求：

1. 学生独立列出计算公式，得出计算结果；

2. 在小组里交流、批阅。

评分要求：能根据大小月进行计算，但计算错误得1分；能根据大小月进行计算，能根据平闰年进行2月天数的计算，但计算错误得2分。

新课程标准倡导在教学设计时应注重知识间的结构性联系，体现知识建构的整体性和一致性。教师以一道开放的思考题，将散碎的知识点综合起来，让学生借助已有知识进行解决，才能更好地实现教学目标，攻破教学重点、难点，构建省时、高效的数学课堂，增强学生思维的系统性。

基于深度学习视域下的小学数学教学设计在学生与数学本质间构建了一座思维的桥梁，学生能够在问题中优化自身的数学学习，在横向上体会知识的来龙去脉，在纵向上领悟知识背后的思想，在厚度上发展抽象能力、推理能力、创新能力，促进自身思维品质的发展，使数学学习走向深入。

参考文献：

［1］ 刘月霞，郭华. 深度学习：走向核心素养（理论普及读本）［M］. 北京：教育科学出版社，2018.

［2］ 马云鹏，吴正宪. 深度学习：走向核心素养［M］. 北京：教育科学出版社，2019.

［3］ 中华人民共和国教育部. 义务教育数学课程标准（2022年版）［M］. 北京：北京师范大学出版社，2022.

［4］ 孙双金. 深度学习与批判性思维的研究［J］. 江苏教育，2019（01）：7-9.