大范围弱刚性运动模拟系统的振动特性分析与振动抑制方法

朱世清，连荫俊，郝永波,3，李 博，臧立彬

（1.北京控制工程研究所，北京 100190； 2.天津航天机电设备研究所，天津 300301；3.天津市微低重力环境模拟技术重点实验室，天津 300301）

0 引言

空间飞行器在轨服务与维护是未来航天发展的重要方向，也是航天领域研究的热点之一[1-9]。应用在轨服务飞行器执行任务之前，必须对其开展半物理仿真和全物理仿真，以验证其控制策略及执行效能。为在地面微重力模拟环境下对空间飞行器进行有效验证，需建立一个大范围运动模拟半物理仿真平台[10]，以模拟服务目标（中小型）在复杂初始运动条件下被操作时的运动学过程。但在地面上进行运动模拟时，机械传动部件之间的摩擦、运动系统控制精度和反馈控制中的动态响应误差等会使运动模拟系统产生振动[11-12]；尤其对于大范围运动模拟系统，纵向运动的二维平动系统主梁和横向运动的小车在急停或启动时产生的惯性力容易诱发系统的振动[13]。此外，由于质量受控，大跨度系统刚性降低，系统动态运行时含有复杂的激励源，如二维平动系统起停和加减速，模拟目标星周期自旋运动等，都可能引起整个运动模拟系统的振动。

有文献提出通过减小加速度、增强系统实时性的方法来抑制运动系统的振动，但这种方法会影响系统的响应速度[14]，因此不适用于大范围三维平动系统。通过优化电机系统的PID 参数也可以起到一定的抑振效果，但对于大范围运动模拟系统来说，抑振效果有限[15-16]。

因此，本文通过简化三维平动系统的力学模型，分析系统对惯性激励的响应。探究试验小车在纵向二维平动系统主梁不同位置下的系统响应、固有频率，以及伸缩立柱长度的影响，确定系统振动的主要来源；并提出一种由弹簧、质量块及阻尼器组成的调谐质量阻尼器（tuned mass damper, TMD）抑振方法，并通过仿真分析和实验验证所采用的动能吸振装置的减振效果，旨在减小系统结构破坏的风险，提高系统的运行可靠性。

1 大范围运动模拟系统结构

1.1 三维平动系统组成

大范围运动模拟系统为龙门悬吊式三维平动装置，主要由横向二维平动系统（包括x向主梁和y向试验小车）和竖向平动系统（z向伸缩立柱）等组成，具体结构参见图1。该运动模拟系统的x向运动行程可达60 m，y向运动行程可达40 m。本文通过有限元方法建立该运动模拟系统的精确模型，用来分析在轨服务飞行器运动过程中所产生的振动特性。从图1 还可看到整个龙门悬吊式大范围三维平动装置在GNC 厂房中的布局关系，实验室原二维平动系统（天车）位于南侧，龙门悬吊式三维平动装置位于北侧。大范围三维平动装置用于安装和承载博弈目标运动模拟器（即并联机构和模拟目标星），并实现其在实验室三维空间的大范围平动运动。

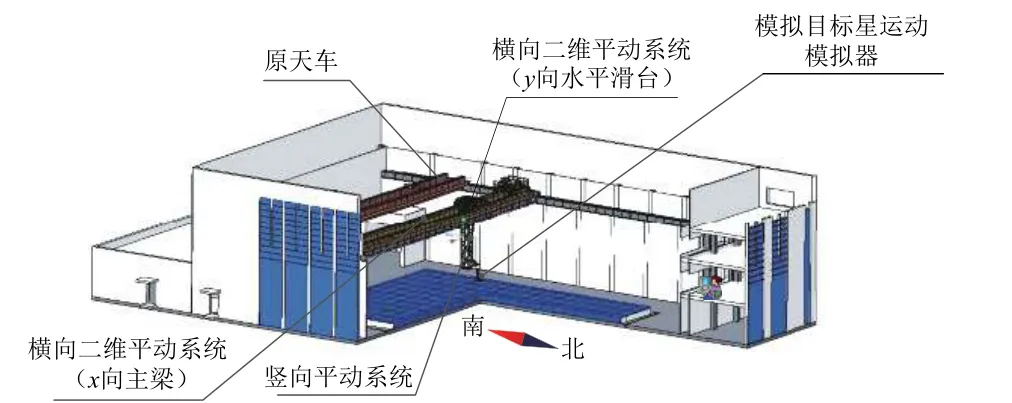
图1 大范围运动模拟系统结构及布局示意Fig.1 Structure and layout of the large-scale kinematic simulation system

1.2 三维平动系统有限元仿真模型

三维平动系统的主梁采用双梁桁架结构，单根桁架梁由4 段拼接而成，拼接处用销轴和高强度铰接螺栓连接固定，梁跨距45.6 m、高度2.1 m、端梁宽度8.0 m，如图2 所示。单段桁架梁采用型材焊接而成，为了减重并提高刚性，桁架梁截面形状设计为三角形：下弦梁选用2 根135 mm×135 mm×12 mm 的方管，上弦梁采用250H 型钢，斜腹杆采用φ76 mm×6 mm 圆管，材料均为Q355B。伸缩立柱同为桁架梁焊接结构，采用100 mm×100 mm×5 mm 的方管焊接而成，材料为Q345 钢。

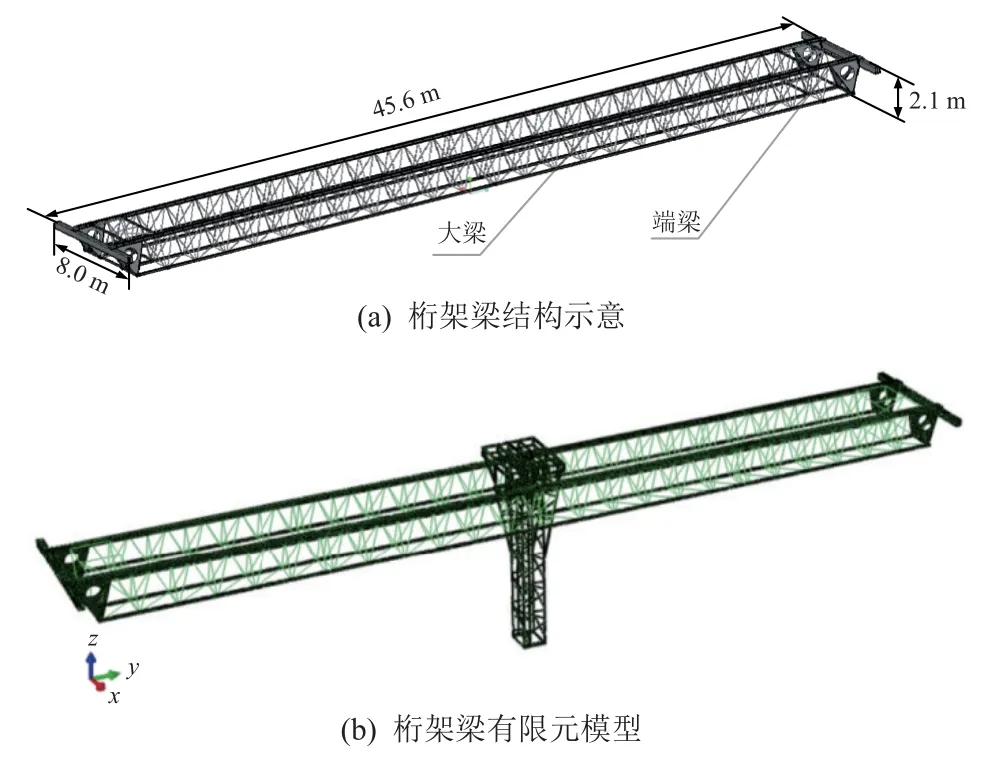
图2 桁架梁结构及有限元模型Fig.2 Structure and finite element model of the truss beam

为分析桁架梁刚度，边界条件定义如图3 所示，梁结构作简支约束，分析时计算带载和不带载2 种工况，带载时单根主梁的承载为10 t/2=5 t，载荷与桁架主梁的z向距离为5.6 m。

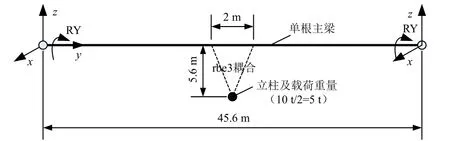
图3 桁架梁边界条件设置Fig.3 Boundary condition setting for the truss beam

在建立模型前，为便于仿真分析，对系统做如下简化：

1）去除纵向大车行走平台的4 个车轮，在车轮与水平滑台的4 个接触圆柱面处添加固定约束；

2）将水平滑台和纵向二维平动系统主梁之间的轮-轨接触改为面-面接触；

3）将立柱和博弈目标运动模拟器（即并联机构和模拟目标星）用等效质量块替代。

2 系统静态载荷、振动模态及响应分析

2.1 系统静态载荷及振动源介绍

为简化双梁计算，采用荷载减半的形式分析单梁变形情况，二维平动系统中段承载竖直向下5 t载荷（加载方式见图4(b)）和空载时的桁架梁变形如图4 所示。仿真结果显示二维平动系统最大变形发生在中段，桁架梁整体因载荷作用呈向下弯曲的形态，空载和5 t 载荷下的最大变形分别为46.1 mm和78.1 mm。

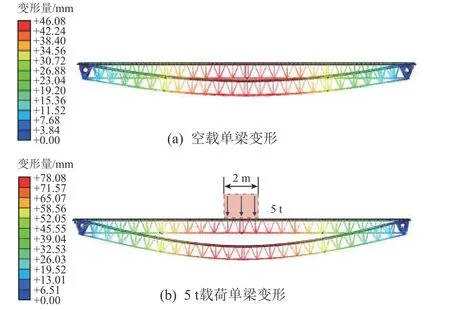
图4 桁架梁静态载荷及形变分析Fig.4 Static load and deformation analysis of the truss beam

由于该运动模拟系统具有多个自由度运动，振动来源比较复杂，主要有：

1）纵向运动的二维平动系统主梁和横向运动的小车在启动或刹车/急停时产生的惯性力；

2）模拟目标星高速旋转过程中由于不平衡产生的简谐振动；

3）并联机构作动时产生的简谐激励。

2.2 系统振动模态计算

试验小车在主梁上运动到不同位置时，主梁的变形是不同的；伸缩立柱伸长量不同时，立柱结构的尺寸和刚度均发生变化。可见，整个结构的基频是随着运动工况发生变化的，系统为一个变结构系统。因此，运动系统的模态分析应针对不同工况分别进行。

2.2.1 工况划分和编号

按试验小车在主梁上的位置和伸缩立柱长度对系统的工况进行划分和编号，详见表1。

表1 工况编号Table 1 Numbering of working conditions

2.2.2 模态分析结果

计算不同工况下运动系统前6 阶固有频率，如表2 所示。分析表中数据可知：当伸缩立柱长度保持不变时，试验小车偏离主梁中心的距离越大，运动系统的后4 阶固有频率就越小，而对前2 阶固有频率影响不大；当试验小车在主梁上的位置保持不变时，伸缩立柱长度对后4 阶固有频率影响不大。

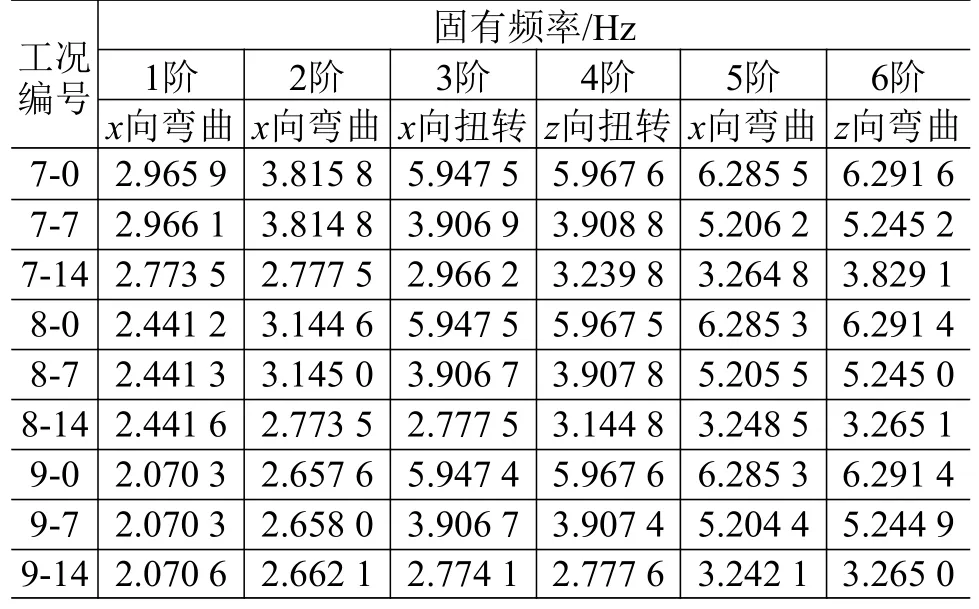
表2 系统模态频率Table 2 System modal frequencies

2.3 系统振动响应分析计算

2.3.1 材料及边界条件设置

进行有限元仿真分析时，首先要设置模型各部分材料属性，添加边界条件，进行网格剖分处理等。

1）将二维平动系统主梁、试验小车、伸缩立柱和并联机构的材料设置为结构钢，将模拟目标星等效为质量块；

2）将模型中的全部装配接触关系（即所有接触面）均设为Bonded 类型；

3）对于约束条件，在承载轮与试验小车的4 个接触圆柱面处添加固定约束。

2.3.2 载荷设置

如2.1 节所述，引起振动的载荷主要有惯性力、模拟目标星偏心旋转激励和并联机构简谐激励。

1）惯性力

根据实际工况，给予系统x向和y向大小为0.2 m/s2的加速度载荷，载荷为阶跃函数。

2）模拟目标星偏心旋转激励

模拟目标星质量为200 kg，质心偏心100 mm，自旋角速度为65 (°)/s。在模拟目标星自旋过程中，由于偏心产生的激励可以分解为沿y向和沿z向的简谐激励fy和fz，均为正弦激励函数。

3）并联机构简谐激励

根据并联机构的作动能力，最大可使平台z向产生0.1 mm 的位移，频率为10 Hz。因此在仿真分析时给予并联机构一个幅值0.1 mm、频率10 Hz 的简谐位移激励。

2.3.3 结果分析

不同工况在3 种激励分别作用下，伸缩立柱末端的响应如表3 所示。分析表中数据可知，主振动方向是由主梁x向作动引起的。因此减振器的功能应为减少卫星等效质量块沿x方向、频率为2 Hz 的振动，这符合弱刚性模型的假设，可以采用TMD来抑制振动。

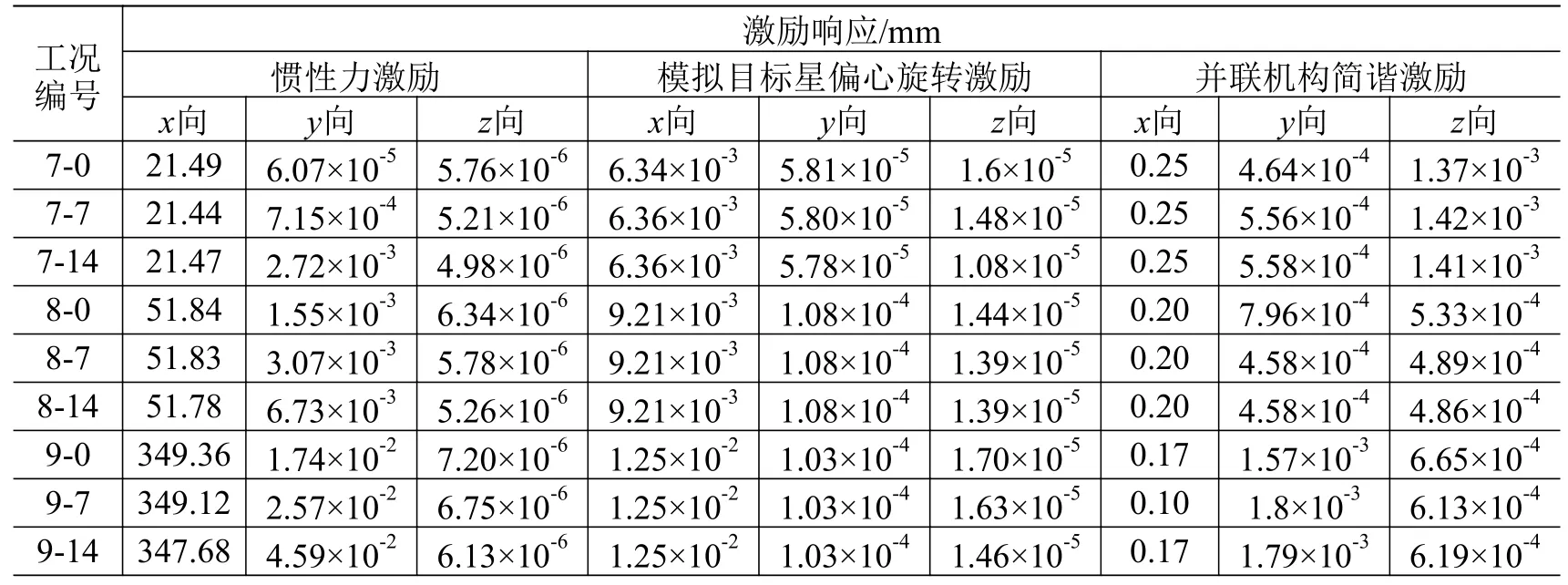
表3 伸缩立柱末端在3 种激励下的响应Table 3 Response of telescopic rod end under three excitations

3 减振理论及实际效果分析

通过分析得知，模拟目标星的偏心、并联机构以及惯性力均会对系统产生振动激励，且均会导致主梁发生x、y、z三个方向的形变，其中x向激励产生的振动幅值最大。若减振系统可以实现x方向的振幅减小，则可以在其余两方向也加装减振系统以实现振动隔离。因此本文将作用在主梁上x方向的激励作为振动的主要激振力，采用TMD 来吸收主梁所受到的振动激励。

3.1 减振模块理论分析

在待减振结构上安装TMD 实现振动隔离的系统可以等效为二自由度系统，其理论模型见图5。图中m1、k1、c1、x1分别为系统主结构的质量、弹簧刚度、阻尼系数、位移响应；m2、k2、c2、x2分别为TMD 系统的质量、弹簧刚度、阻尼系数、位移响应；F0表示系统施加的外部激励。

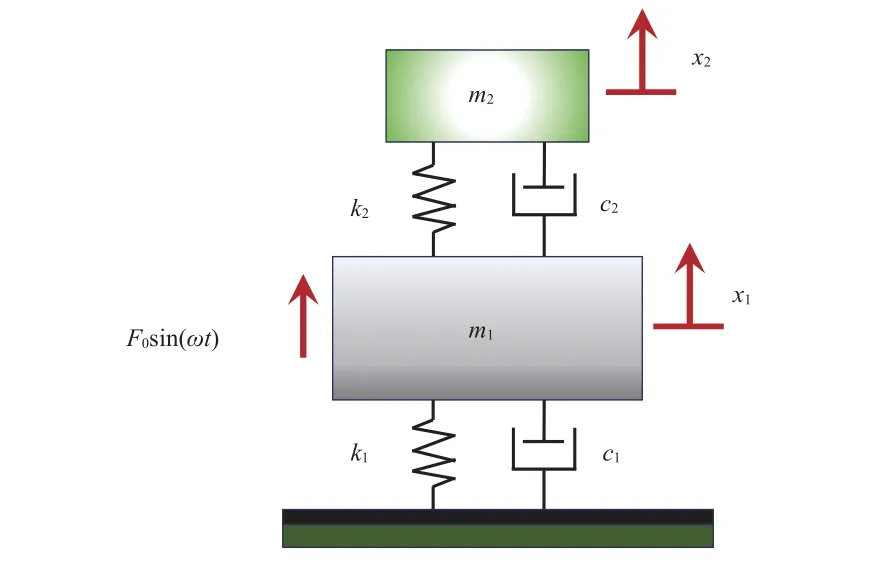
图5 TMD 理论简化模型Fig.5 Theoretically simplified model of TMD

将TMD 安装在系统主结构上，主要是将弹簧和阻尼器连接到待减振结构上，则在外部激励作用下，待减振结构与 TMD 同时振动，TMD 振动会吸收待减振结构的振动能；此外，由于 TMD 的调谐减振使原有系统在共振频率处的振幅减小，故可降低共振对原有系统造成的破坏。

建立图5 所示二自由度振动系统动力学模型[17]

根据文献[17]，获得主系统位移振幅比量纲为1 的表达式

其中：μ为等效质量比，μ=m2/m1；s为激振力与主系统固有频率之比；α为TMD 与主系统固有频率之比；ζ为阻尼比。

3.2 TMD 结构设计及减振效果

根据3.1 节的理论分析，对TMD 进行设计，取质量比μ=0.02，阻尼比ζ=0.1，频率比s=0.98。TMD主要由1 个质量块、4 根弹簧以及2 个阻尼器组成，外形尺寸为550 mm×500 mm×500 mm，结构如图6 所示。

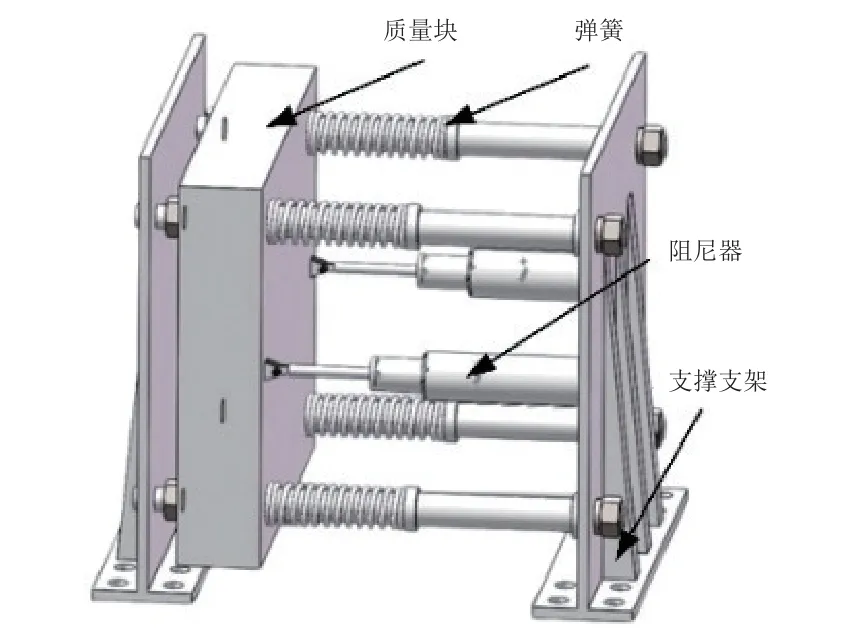
图6 TMD 结构三维模型Fig.6 Three-dimensional model of the TMD structure

为探究TMD 对主梁的减振效果，将所设计TMD 安装在伸缩立柱根部，对系统在惯性载荷激励下x方向上的振动情况进行仿真，结果如图7 所示。可以看到，TMD 能够在固有频率范围内实现对系统（x方向）的有效减振，大幅降低振动幅值。

图7 TMD 对主梁x 方向振动的抑制效果Fig.7 Suppresing effect of TMD on x direction vibration of the main beam

4 结束语

本文针对在轨服务目标星大范围运动模拟系统低频振动问题，通过仿真方法研究了运动模拟系统振动机理，提出振动抑制方法。首先分析了不同运行工况下的系统响应、固有频率以及激励分别作用时模拟目标星在各个方向上的最大位移，确定了系统振动的主要来源；然后设计TMD 来降低系统振动幅值以提高系统稳定性。研究结果表明：在不同运行工况下，系统的固有频率不同，为变结构系统；采用TMD 可以有效抑制系统振动，降低系统发生共振的风险，进而提高系统的运行可靠性。