基于CNN 和LSTM 的航天用涂层型自润滑关节轴承寿命预测及可靠性评估

刘云帆，林亮行，马国政，孙建芳，苏峰华，郭伟玲，朱丽娜，王海斗,4

（1.中国地质大学（北京） 工程技术学院，北京 100083；2.陆军装甲兵学院 装备再制造国防科技重点实验室，北京 100072；3.华南理工大学 机械工程学院，广州 510000；4.陆军装甲兵学院 机械产品再制造国家工程研究中心，北京 100072）

0 引言

自润滑关节轴承是一种无需补充润滑剂的特殊关节轴承，在其相对运动表面涂（镀）或黏结有一层固体润滑材料，可以起到减小摩擦阻力、延长轴承寿命的作用[1-6]。应用于各类航天器机构中的关节轴承通常会面临着高真空、高低温循环、原子氧及紫外辐射等极为苛刻的服役环境[7-8]。因此，研究人员尝试将一些具有优异真空摩擦学性能的固体润滑材料（层状化合物、非晶碳基薄膜等）以涂层的形式运用至关节轴承表面[9-13]，来提高轴承在空间环境下的服役寿命和可靠性。目前，涂层型自润滑关节轴承这一新型轴承已广泛应用于航天装备中的重要基础运动部件；对其服役寿命进行准确预测和可靠性评价是航天装备研制中的重要工作。

关节轴承的服役寿命及可靠性研究一直以来都是轴承相关研究中的重点[14-16]。针对传统的衬垫型关节轴承，国外的SKF、NTN、INA 以及FLURO等著名轴承公司很早就提出了适用于各自产品的轴承寿命计算公式[17]。同时，杨咸启等[18-19]引入设计制造质量系数，建立了一套适合于国产关节轴承的寿命计算方法，并推进颁布了JB/T 10860—2008标准，有力推动了国内关节轴承寿命计算方法的标准化进程。进一步地，邱明团队[20-21]基于组合磨损理论建立了衬垫型自润滑关节轴承的磨损寿命计算模型，并基于两参数Weibull 分布模型以磨损量作为退化量对轴承进行可靠性评估。为缩短加速寿命试验的时长，邱明团队[22]设计了双加速应力试验方案对关节轴承在重载高频工况下的服役可靠性进行评估，结果表明轴承能在正常可靠度范围内维持长时间服役。杨育林等[17,23]则针对重载低速工况下的衬垫型关节轴承进一步优化了寿命预测模型。然而，现有的关节轴承寿命预测研究主要集中于衬垫型关节轴承，其自润滑衬垫的磨损量通常为mm 量级，但涂层型自润滑关节轴承的自润滑涂层厚度仅有1～5 μm，其磨损量难以由位移传感器精确实时地测量获取，因此不能参考传统的衬垫型关节轴承利用磨损量作为退化信息进行寿命预测和可靠性评估[21]。基于一些对滚动轴承的失效研究[24-26]以及我们的前期工作[27-28]可以发现，摩擦扭矩能够较好地反映关节轴承摩擦接触面在运行过程中的磨损状态，因此可以将扭矩信号作为退化特征来表征涂层型自润滑关节轴承的退化状态。

随着机器学习、深度学习理论的快速发展，基于人工智能技术的寿命预测方法已成为进行机械零部件剩余寿命预测的主要手段之一[29-30]。邱明团队[22]基于灰色神经网络建立了衬垫型关节轴承的寿命预测模型，与传统BP 神经网络模型相比，该模型将轴承预测寿命的平均相对误差降至3.9%。长短期记忆（LSTM）神经网络对时间序列有很高的敏感度，近年来在滚动轴承的寿命预测领域得到广泛应用。比较具有代表性的是Hotait 等[31]对滚动轴承采集特征进行主元分析及筛选，将特征集合作为训练集输入LSTM 神经网络得到轴承的寿命预测模型，经验证该模型有较好的泛化能力和预测精度。涂层型自润滑关节轴承的寿命预测可以借鉴这种较新的思路，寻找适合的特征（如摩擦扭矩）建立轴承的寿命预测模型。由于振动信号具平稳性，滚动轴承多采用时域或频域分析法进行信号特征提取。而涂层型自润滑关节轴承的摩擦扭矩信号为非平稳信号，因此须采用时频域信号分解方法对非平稳信号进行有效处理，以充分挖掘信号所包含的信息，实现信号特征提取[32]。卷积神经网络（CNN）具有收敛速度快、准确率高等优势，且能够挖掘数据中的深层特征[33-34]。CNN 配合LSTM 在处理时间序列应用中的优势，正好能够精确高效地对涂层型自润滑关节轴承剩余寿命进行预测，具备较好的预测精度以及失效预警效果。

近年来，国内部分研究团队虽然已在涂层型自润滑关节轴承状态监测和失效机理研究方面取得了一些成果[22,27]，但并未深入进行轴承的寿命预测和可靠性评估工作，尤其缺乏适用于涂层型自润滑关节轴承的寿命预测方法。基于上述研究背景，本文针对涂层型自润滑关节轴承，以摩擦扭矩信号为原始输入，提出一种CNN 与LSTM 相结合的关节轴承寿命预测方法，以期为航天用涂层型自润滑关节轴承的可靠性评价、服役状态监测和在线维护提供理论依据和方法借鉴。

1 基于CNN 和LSTM 的涂层型自润滑关节轴承寿命预测模型

1.1 CNN 模型及特征提取原理

涂层型自润滑关节轴承的工作环境复杂多变，因而其摩擦扭矩信号具有非平稳、随时间变化的特点。本文首先利用CNN 对涂层型自润滑关节轴承的摩擦扭矩信号进行特征提取，其卷积层输出为

式中：xl(rj)为第l层中第j个卷积计算的局部序列r；为第l层的第i个卷积核的第j′个权值； *为卷积运算符，W为卷积核的宽度，在一维卷积中表现为覆盖区域信号的长度。

然后，使用ReLU 激活函数对yl(i,j)进行处理，

式中，al(i,j)为yl(i,j)经激活函数处理后的结果，f代表激活函数。

之后，还需要通过池化层对al(i,j)进行特征降维处理，本文中采用最大值池化方法，令

式中：al(i,t)为第l层第i个特征的第t个神经元输出激活值；V为池化宽度。

1.2 LSTM 模型原理

为能准确预测涂层型自润滑关节轴承的服役寿命，选用LSTM 模型进行剩余寿命预测，该模型能够有选择性地添加新的信息或者遗忘先前的信息[35]。LSTM 模型结构如图1 所示。

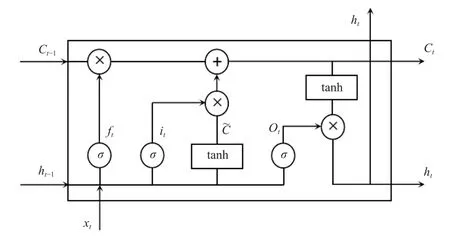
图1 LSTM 模型结构Fig.1 Structure of LSTM model

t时刻LSTM 的输入为序列xt，隐藏层t-1 时刻状态为ht-1，记忆单元t-1 时刻状态为Ct-1，经过激活函数σ计算可得，

式中：ft、it和ot分别为遗忘门、输入门和输出门的计算结果；Wf、Wi和Wo分别为三者的权重矩阵；bf、bi和bo分别为三者的偏置项。

在t时刻后，更新后的状态Ct以及隐藏层状态ht为

式中：C～ 为候选状态更新值；Wc和bc分别为更新后的权重矩阵和偏置项；符号◦ 表示按元素乘。

1.3 基于加速寿命试验的涂层型自润滑关节轴承寿命预测模型的建立

涂层型自润滑关节轴承需要通过分析其摩擦扭矩信号的变化，利用CNN 提取扭矩信号中的失效特征，然后由LSTM 模型实现对涂层型自润滑关节轴承剩余寿命的准确预测。图2 所示为本文提出的涂层型自润滑关节轴承寿命预测流程。

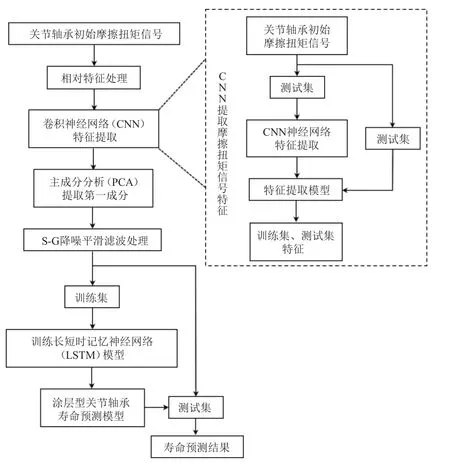
图2 涂层型自润滑关节轴承寿命预测流程Fig.2 Flow chart for life prediction of coated self-lubricating spherical bearings

具体流程如下：

1）使用扭矩传感器对涂层型自润滑关节轴承的摩擦扭矩信号进行采集，并选取不同工况下的扭矩值作为训练集。

2）对摩擦扭矩信号进行相对值处理，采用相对特征来表征轴承的失效状态，从而消除不同工况下关节轴承退化过程中摩擦扭矩的变化差异。

3）将步骤2 中的摩擦扭矩值作为CNN 的输入，通过多层CNN 对扭矩信号进行特征提取，得到能够表征关节轴承全寿命周期的信号特征，详细计算过程参考2.1 节。

4）对CNN 所提取的摩擦扭矩信号特征进行主成分分析（PCA），将信号特征重新组合成一组新的综合变量，从而实现数据降维、减少计算量，获取能够表征轴承失效过程的第一成分。

5）将信号特征输入LSTM 模型前利用Savitzky-Golay（S-G）滤波法进行降噪平滑处理，将处理后的特征输入LSTM 神经网络进行训练，构建寿命预测模型。其中，训练数据中退化节点前的轴承寿命设置为1，退化节点后轴承剩余寿命需经过Min-Max标准化处理；最后采用均方误差（MSE）以及平均绝对误差（MAE）对寿命预测模型的预测精度进行评估。

2 航天用涂层型自润滑关节轴承加速寿命试验及结果分析

2.1 加速寿命试验方案及平台

为验证本文所提出的轴承寿命预测模型效果，首先在低速摆动磨损寿命试验机上进行轴承加速寿命试验以获取关节轴承寿命数据。具体采用高精度的扭矩传感器对摩擦扭矩信号进行采集，设定每间隔120 个摆动周期采集1 次扭矩最大值[27]。试验所用轴承为自制的涂层型自润滑关节轴承，型号GE17E/HEK，且为同一批次生产。轴承实物和结构如图3 所示，内圈外球面涂层为双层a-C:H/MoS2薄膜，外圈内球面涂层为a-C:H 薄膜。

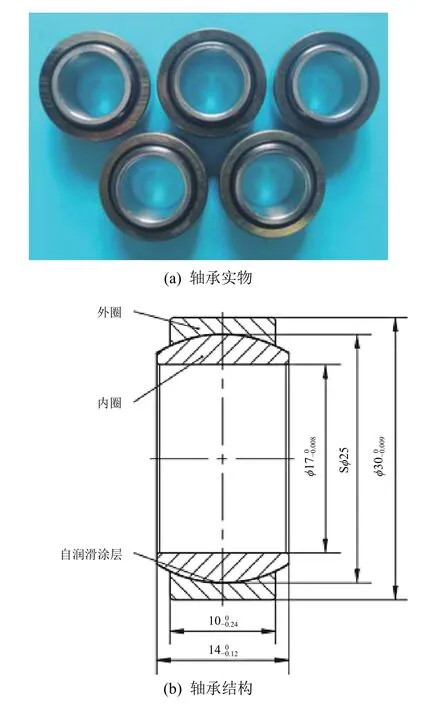
图3 GE17E/HEK 涂层型自润滑关节轴承Fig.3 GE17E/HEK coated self-lubricating spherical bearing

加速寿命试验方案要点如下：1）在常温常压环境下进行；2）试验机的固定摆动角度为±10°，摆动频率为2.0 Hz；3）基于设备条件，加速试验为恒定单一应力加速寿命试验，加速应力为径向载荷，设置4 个加速应力等级（分别为100 N、200 N、300 N 和500 N），每个加速应力下的重复组数为4 组；4）前期研究中发现当轴承在运行过程中出现扭矩信号明显上升或突变时说明轴承已经发生磨损失效，因此在加速寿命试验中设定，当轴承扭矩上升为平均值的1.5 倍以上且持续时间超过5 min 时判定轴承失效，停止试验。表1 所示为加速寿命试验参数及试验结果。

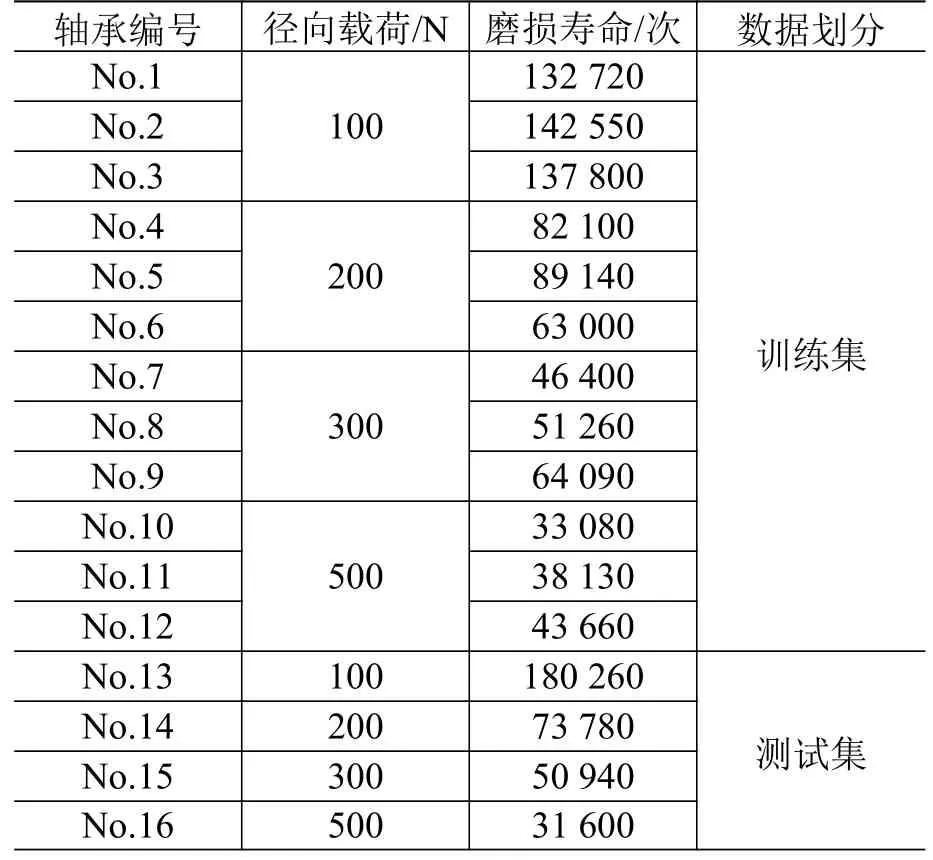
表1 加速寿命试验结果Table 1 Accelerated life test results

2.2 涂层型自润滑关节轴承寿命预测结果与分析

如表1 所示，将轴承No.1～No.12 的测试数据作为训练集，轴承No.13～No.16 的测试数据作为测试集。按照图2 所示的流程将原始摩擦扭矩值作为输入，将经过预处理后的扭矩值输入多层CNN中，CNN 的主要结构参数如表2 所示。利用CNN对摩擦扭矩信号中能够表征轴承失效状态的特征进行提取，以100 N 工况为例，CNN 处理后的结果如图4 所示。

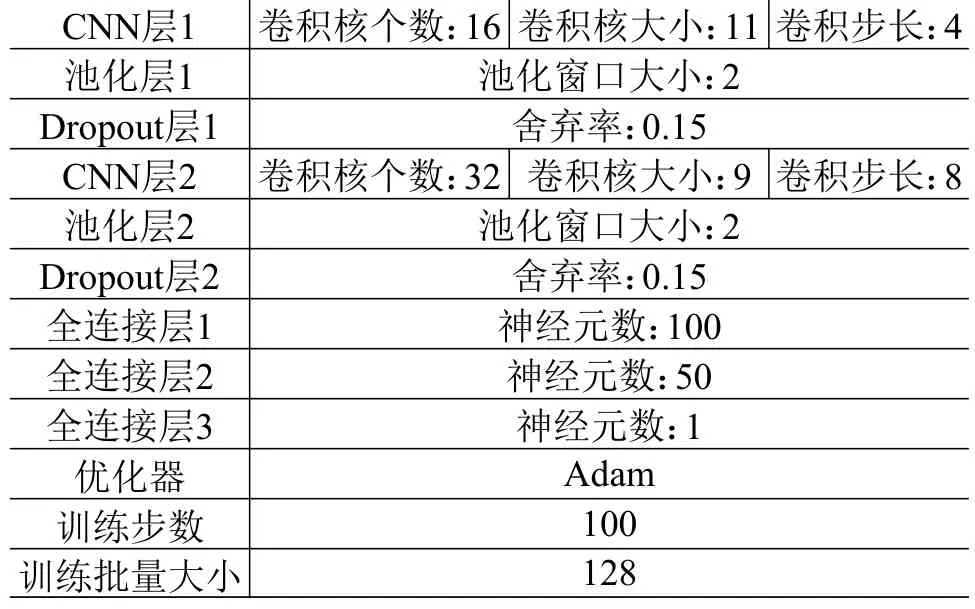
表2 CNN 结构及训练参数Table 2 CNN structure and training parameters

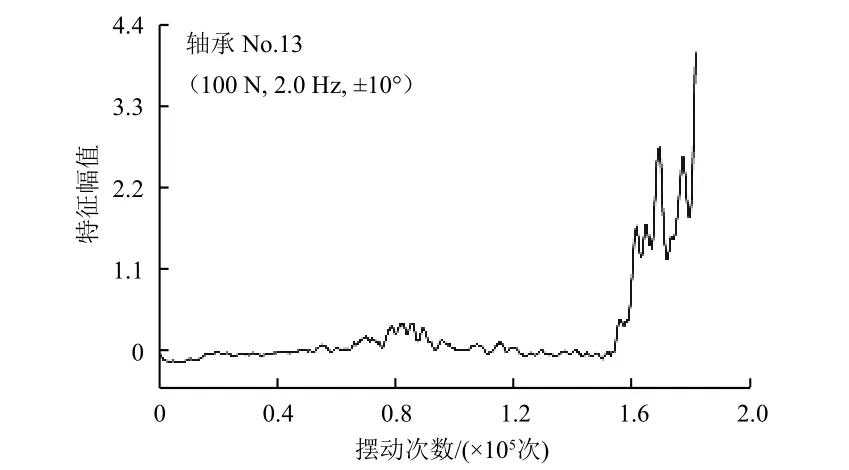
图4 CNN 对100 N 工况下轴承摩擦扭矩信号的特征提取结果Fig.4 Feature extraction results of bearing friction torque signal under 100 N by CNN

随后对提取的特征信号进行PCA，其中本文所提取的第一成分方差贡献率均大于90%，将经过S-G降噪平滑处理后的特征输入本文建立的涂层型自润滑关节轴承寿命预测模型中。LSTM 的主要结构参数如表3 所示，采用Adam 优化器，为提高预测模型的训练精度及速度，初始学习率设置为0.001；为防止预测模型过拟合，选用舍弃率表征模型中记忆体单元被暂时舍弃的概率，并将舍弃率设置为0.3；为提高收敛速度和预测趋势的准确度，训练步数和批量大小分别设置为200 和128。如图5 所示，寿命预测模型的收敛速度较快，且随着训练次数的增加，训练集误差与测试集误差逐渐降低，最小误差低于0.02 并趋于稳定，表明模型收敛性好。

表3 LSTM 结构及训练参数Table 3 LSTM structure and training parameters

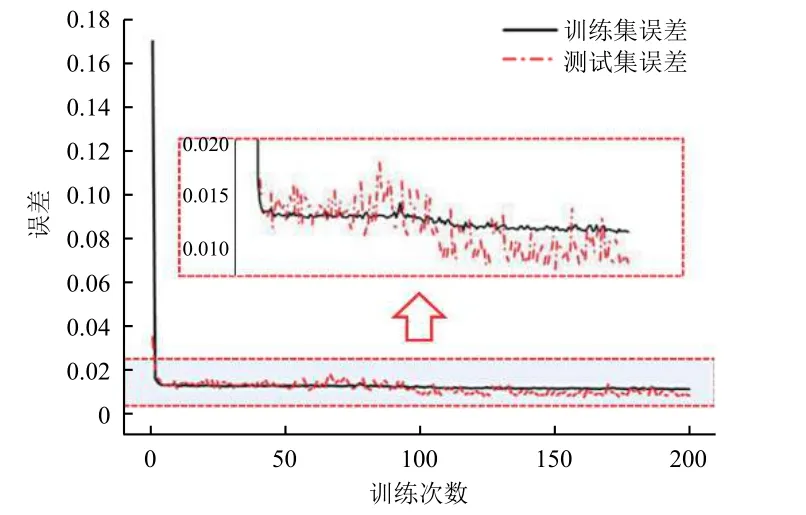
图5 CNN+LSTM 模型在训练集和测试集上的误差曲线Fig.5 Error curves of CNN+LSTM model in training set and test set

为验证CNN+LSTM 模型的预测效果，将传统LSTM 模型作为对比模型。测试集（轴承No.13～No.16）的寿命预测结果如图6 所示，可以看到，在稳定服役阶段，LSTM 对轴承寿命的预测误差较大，而CNN 的引入则较大程度上提升了LSTM 对轴承稳定期寿命的预测精度；在服役后期，虽然两种模型的寿命预测精度都得到了一定程度的提升，但CNN+LSTM 模型对实际寿命数据的拟合效果显然更为精确。以上结果说明，相较于传统LSTM 模型，CNN+LSTM 模型实现了对不同加速应力下轴承全阶段服役寿命的高精度拟合。

图6 CNN+LSTM 模型和传统LSTM 模型对不同加速应力下轴承剩余寿命的预测结果对比Fig.6 Comparison of prediction results of CNN+LSTM model and traditional LSTM model on bearing residual life under different acceleration stresses

为进一步考察CNN+LSTM 模型的剩余寿命预测精度，本文任意选取归一化剩余寿命比例0.3 为检验点。两种模型的剩余寿命预测结果如图6 和表4 所示，CNN+LSTM 模型对检验点剩余寿命预测误差远小于传统LSTM 模型，与检验点的实际剩余寿命相比，CNN+LSTM 模型的最大预测误差仅为4145 次；同时对轴承全寿命预测相对误差也控制在6%以内，最小仅为0.79%。而传统LSTM 模型对检验点的剩余寿命误差最大为13 834 次，各加速应力下对轴承全寿命预测误差均大于CNN+LSTM模型。预测结果表明，引入的CNN 能够发挥其自身优势，深层次挖掘涂层型自润滑关节轴承摩擦扭矩信号的失效特征，从而较大程度提高了LSTM 模型的寿命预测精度。

表4 预测模型的寿命预测精度比较Table 4 Comparison of life prediction accuracy among models

采用MSE 和MAE 两项指标对CNN+LSTM 和传统LSTM 寿命预测模型的预测精度进行评估，结果如表5 所示。相比于传统LSTM 模型，本文所建立的CNN+LSTM 模型的预测精度有较大的提升，CNN+LSTM 模型对轴承预测寿命的MSE 值降低最大约74.4%，MAE 值降低最大约53.5%。以上指标对比表明，本文所建立的CNN+LSTM 寿命预测模型能够较为准确地对涂层型自润滑关节轴承的服役寿命进行预测，通过人为设置检验点也能较为准确地实现对涂层型自润滑关节轴承剩余寿命的预测，这为在实际应用中指导航天机构中的关节轴承的及时更换和维护提供了一定的理论依据。

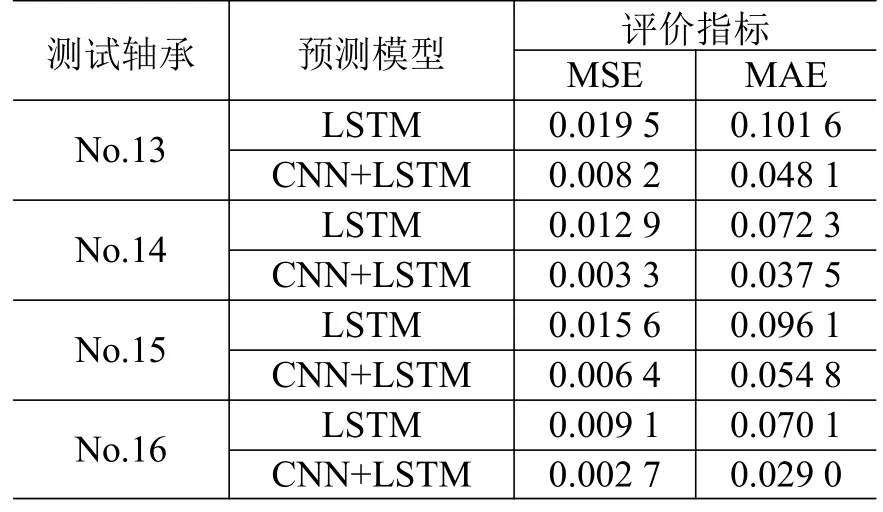
表5 寿命预测模型的预测精度评估Table 5 Life prediction accuracy evaluation of models

2.3 基于加速寿命试验的涂层型自润滑关节轴承可靠性评估

在加速寿命试验的基础上，采用两参数Weibull分布模型[14,20,36]对涂层型自润滑关节轴承的可靠性进行评估。具体基于以下假设：

假设1——在不同加速应力（径向载荷）下的轴承寿命数据都服从两参数的Weibull 分布，则第i加速应力水平下的概率分布函数为

式中：t为每套轴承的寿命试验时间（单位为次），t＞0；m为形状参数；η为尺度参数（即特征寿命）。

假设2——在不同加速应力下（即低载、中低频范围内）的涂层型自润滑关节轴承的失效机理保持不变，皆为涂层的磨损失效。

假设3——选择逆幂律模型作为涂层型自润滑关节轴承的加速模型[15]，即轴承的加速寿命方程为

式中：η为特征寿命；S为加速应力（径向载荷）；a、b为加速寿命方程的系数。

利用拟合优度检验法对不同加速应力下的轴承寿命进行假设检验，由表6 的检验结果可知，不同加速应力下的Weibull 分布P值都大于0.05，进一步表明加速应力下的涂层型自润滑关节轴承的寿命服从两参数的Weibull 分布，从而验证了假设1的合理性。

表6 不同加速应力下的轴承磨损寿命分布拟合检验Table 6 Fitting test of bearing wear life distribution under different accelerating stresses

在小样本的可靠性评估中，最大似然估计法（maximum likelihood estimation, MLE）的参数估计精度大于最佳线性无偏估计法（best linear unbiased estimation, BULE）[37-38]。因此，本文在关节轴承的可靠性评估中，选择MLE 对Weibull 分布模型中的参数进行估计，见表7，其中m值处于合理范围内[22]，结合前期试验结果也进一步表明不同加速应力下的轴承失效机理并未发生改变[27]，验证了假设2的合理性。

表7 不同加速应力下的可靠性模型参数估计值Table 7 Estimates of reliability model parameters under different acceleration stresses

基于以上的参数，可以得到不同加速应力下的涂层型自润滑关节轴承可靠度曲线，如图7 所示。以100 N 应力载荷下的可靠度曲线为例，可以看到：GE17E/HEK 型关节轴承的可靠度在服役初期下降极其缓慢，始终保持在较高水平；而随着服役时间的延长，其可靠度逐步降低且下降速率逐渐加快，表明在服役后期轴承会迅速发生失效。这也进一步说明，在轴承的稳定磨损阶段后期，轴承相对运动表面遭受了较为严重的磨粒磨损，涂层在短时间内迅速被磨损掉，基体也随之裸露，最终导致轴承失效[28]。

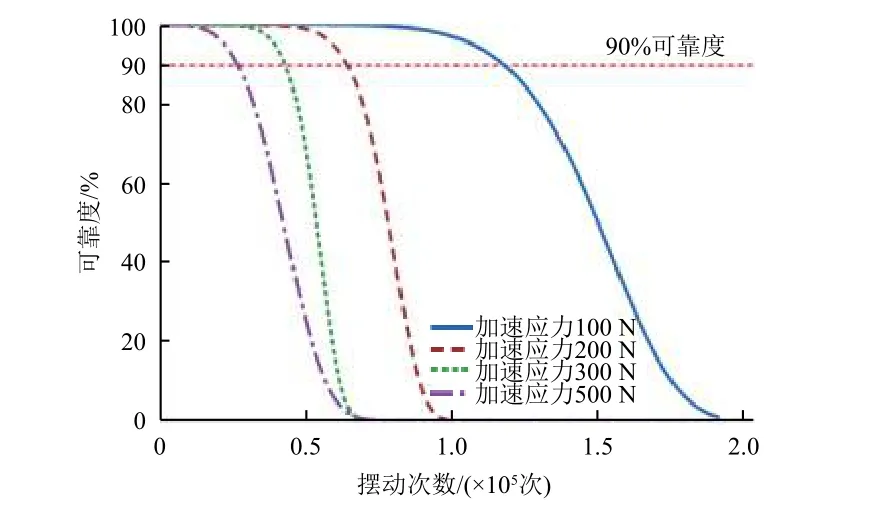
图7 不同加速应力下的涂层型自润滑关节轴承可靠度曲线Fig.7 Reliability curves of coated self-lubricating spherical bearings under different acceleration stresses

涂层型自润滑关节轴承加速寿命拟合曲线如图8 所示，加速寿命方程（式(7)）中系数a、b的拟合值分别为16.22、-0.921 6，拟合确定系数R2为0.998 3，说明加速模型拟合效果较好，逆幂律加速寿命方程能够较好地描述加速应力与轴承寿命间关系，验证了假设3 的合理性。

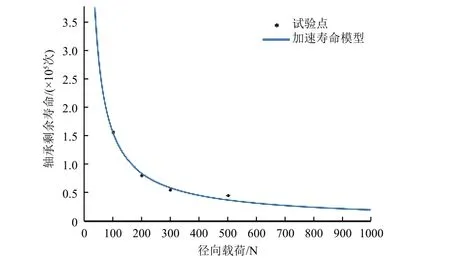
图8 涂层型自润滑关节轴承的加速寿命模型拟合曲线Fig.8 Fitted curve of acceleration life model for coated selflubricating spherical bearings

另外，由图7 可以看到，在100 N、200 N、300 N 和500 N 加速应力下，GE17E/HEK 型关节轴承可靠度为90%时对应的寿命分别为117 394 次、64 115 次、42 906 次和26 558 次。这说明在对应相同的可靠度要求时，随加速应力的增大，关节轴承的寿命呈现急剧下降的趋势，同时在高可靠度水平（90%）下的维持时间也呈现递减趋势，进一步表明GE17E/HEK型关节轴承更适合在较低载荷范围内服役，在较高载荷下的服役可靠度并不高。

对比传统衬垫型关节轴承的可靠度曲线[22]，可以发现涂层型自润滑关节轴承在低载荷范围内保持较高可靠度水平（90%）服役的时间更长；而衬垫型关节轴承一般服役于重载高频工况，且相关研究结果表明其在大部分服役期间内的可靠度水平较低。

3 结束语

本文基于摩擦扭矩信号时序相关性强的特点，提出一种CNN 与LSTM 相结合的涂层型自润滑关节轴承剩余使用寿命预测模型。相较于传统LSTM预测模型，该模型构造及数据处理过程简单，且具有较高预测精度。利用CNN 能够较大程度地挖掘涂层型自润滑关节轴承摩擦扭矩信号的失效特征，结合LSTM 实现对轴承在轻载低频范围内的剩余寿命的准确预测，比传统LSTM 模型的预测精度最高提升约74.4%。而与实际轴承寿命值相比，CNN和LSTM 相结合的方法对轴承全寿命的预测相对误差控制在6%以内。基于加速寿命试验数据，进一步对涂层型自润滑关节轴承的服役可靠性进行评估发现，在低载荷（100 N）工况下，GE17E/HEK 涂层型自润滑关节轴承在其约60%的寿命周期内都能够维持高可靠度水平（90%）服役；而随着加速应力的增大，轴承的可靠度以及工作能力逐渐下降。

已知涂层型自润滑关节轴承的性能主要依赖于自润滑涂层的摩擦学性能，因此在后续工作中为提高此类轴承的服役寿命和可靠性，还需进一步开发综合性能更加优异的自润滑涂层体系。