拖船噪声对拖线阵声呐的干扰特性分析

周 健，宋雪晶1,，刘福臣1,

(1.声呐技术重点实验室，浙江杭州 310023；2.杭州应用声学研究所，浙江杭州 310023)

0 引言

拖曳声呐是拖曳在舰船尾部一定距离并处于水下一定深度的声学探测系统，可以通过主动或被动方式接收来自水面或水下目标的声信号，实现对目标信号的检测和参数估计[1]。当使用拖曳声呐进行目标探测时，由于缆绳长度有限，拖船自噪声作为近场强干扰，会影响声呐的探测性能[2]。马远良等分析研究了浅海环境下拖船自噪声的传播原理，对拖船干扰偏离端射方向进行了解释[3]。李启虎等研究了拖曳平台在浅海环境下的干扰特性[4]。在进行浅海目标探测时，发现拖船自噪声会在靠近端射方向产生干扰，而进行深海目标探测时，发现拖船自噪声除了在靠近端射方向产生干扰外，还会在远离端射方向产生干扰，后者干扰强度弱于前者，但由于干扰区间大以及远场目标信号的强度一般较弱，所以该干扰仍会给拖曳声呐的探测性能带来很大影响。

目前，公开文献中有关深海环境下拖船自噪声对拖曳声呐影响的研究文献较少。本文通过计算机仿真和海试数据分析，研究了线列阵在不同环境下对拖船自噪声的波束响应，并分析了深海环境下远离端射方向干扰出现的主要原因。

1 理论模型

1.1 声传播模型

射线理论通过声线轨迹来计算传播损失，该理论起始于亥姆霍兹(Helmholtz)方程[5]：

式中：c(x)为声速，ω是x0处的声源角频率。为了得到射线方程，假设Helmholtz方程的解为

式(2)通常是发散的称为发散级数，但可以证明，在某些条件下它是精确解的一种渐近近似。对式(2)求导，可得：

由此可以得到：

将这一结果代入Helmholtz方程，并令ω的同次项相等，可得：

式(6)称为程函方程，式(7)称为迁移方程，其中τ和A0分别表示相位和幅度。程函方程可以通过特征值法求解，该方程把声路径长度表示成路径两端点的函数，当两端点在声源和接收点位置时，其对应的声线为本征声线。本征声线确定了射线轨迹，而迁移方程则确定了声波的幅度。由此可以计算每一条本征声线在接收点处的声能，接收点处的声压场即为所有本征声线的声压叠加。

1.2 拖船噪声传播过程

拖曳声呐的工作示意图如图1所示。图1中A表示拖船自噪声的等效点声源、BC表示接收基阵、r为拖船噪声源到第一个接收水听器的水平距离、l为接收基阵的长度、h1，h2和h3分别表示拖船噪声源深度、线列阵深度和海深。

图1 拖曳声呐工作示意图Fig.1 Working diagram of towed sonar

考虑到多次海面海底反射声传播损失较大以及描述的方便性，图1中仅给出了拖船自噪声到达接收基阵的3种主要声传播路径，分别为直达声、一次海面反射声和一次海底反射声，其对应的入射角分别为α、β和γ。从图1中可以看到3种声传播路径到达线列阵的入射角不同，而这些不同的入射角将影响线列阵对拖船自噪声的波束响应。根据几何关系可以得到图1中不同声线入射角α、β和γ的计算公式为

当其他参数不变时，通过式(8)可以得到如下规律：(1)随着拖船噪声源深度h1的增加，α、β逐渐减小，γ逐渐增大；(2)随着接收基阵深度h2的增大，α、γ逐渐增大，β逐渐减小；(3)随着海深h3的增大，α、γ保持不变，β逐渐增大；(4)随着水平距离r的增大，α、β和γ均逐渐减小。由于海深是区别浅海和深海环境的主要标准，而根据规律(3)，海深仅影响β，所以理论上海底反射声是造成浅海和深海环境下线列阵对拖船自噪声波束响应不同现象的主要原因。

1.3 宽带频域波束形成

假设基阵接收到的信号为

其中：N为阵元数，xm(t)表示第m个水听器接收到的样本数据。将接收信号傅里叶变换后得到的宽带信号划分为L个子带，每个子带需满足窄带信号的要求即时间带宽积远小于1，则第k个子带的频域表示为

式中：Xm，k(fk)表示第m个水听器在第k个子带的频域数据。对每个子带的频域数据进行加权求和，则第k个子带的输出结果为

其中：H表示共轭转置；w(fk)为加权向量，对于水平均匀线列阵w可以表示为

则宽带信号的频域波束输出结果为

波束输出功率为

其中：θ为波束指向角，当波束指向角θ和来波方向θ0相同时，P(θ)有最大值，此时对应的方位角θe为信号的方位谱估计结果。

2 仿真分析

2.1 仿真条件

仿真分为浅海和深海两种水文环境，利用宽带点源信号模拟拖船噪声源。浅海环境下采用如图2(a)所示的均匀声速剖面，并设置拖船噪声源到线列阵第一个水听器的水平距离r为1 000 m，拖船噪声源和线列阵的深度h1和h2分别为7 m和30 m，海深h3为100 m，采用简正波模型进行声场计算。深海环境下采用如图2(b)所示的Munk型声速剖面，r设置为1 000 m，声线出射角为-90°～90°，拖船噪声源和线列阵的深度h1和h2分别为7 m和100 m，海深h3为2 000 m，由于r相较于海深h3较小，所以利用射线模型进行声场计算。

图2 浅海和深海环境的典型声速剖面Fig.2 Typical sound velocity profiles in shallow and deep sea environments

2.2 仿真结果

2.2.1 浅海仿真结果

利用简正波模型进行声场计算，模拟基阵接收到的拖船噪声信号，并根据常规波束形成算法得到线列阵对拖船自噪声的波束响应。通过改变拖船噪声源深度h1、线列阵深度h2、拖船噪声源到第一个水听器的水平距离r、水听器的间距d、拖船噪声源频率f，研究浅海环境下的拖船干扰特性。

改变拖船噪声源深度h1和线列阵深度h2，得到的仿真结果分别如图3和图4所示。

图3 改变拖船噪声源深度时，线列阵对拖船噪声波束响应的仿真结果Fig.3 Simulation results of the beam response of the linear array to the self-noise of tow-ship when changing the depth of noise source

图4 改变线列阵深度时，线列阵对拖船噪声波束响应的仿真结果Fig.4 Simulation results of the beam response of the linear array to the self-noise of tow-ship when changing the depth of line array

图3中当拖船噪声源的深度由3 m逐渐增加到9 m，线列阵的最大波束响应Pmax分别为-34.37、-31.89、-32.03、-34.38 dB，线列阵在端射方向的波束响应P0分别为-37.09、-34.34、-34.08、-35.76 dB，最大波束响应所对应的方位角与端射方向的夹角即偏离角Δθ分别为12.5°、11.8°、11.1°和10.4°，记Pmax和P0之间的幅度差为ΔP。图4中当线列阵深度由20 m逐渐增加到40 m，线列阵的最大波束响应Pmax分别为-30.07、-34.61、-32.03、-31.8、-31.98 dB，线列阵在端射方向的波束响应P0分 别 为-31.87、-36.09、-34.08、-33.24、-33.37 dB，偏离角Δθ分别为11.1°、11°、11.1°、11°和10.6°。

由上述可得，在该仿真条件下，若线列阵深度保持不变，随着拖船噪声源深度的增大，偏离角Δθ和幅度差ΔP逐渐减小，线列阵最大波束响应Pmax和端射方向的波束响应P0先增大再减小。当拖船噪声源深度保持不变，随着线列阵深度的增加，偏离角Δθ先小幅上下波动再略有减小，而Pmax、P0和ΔP与线列阵深度的关系并不明显。

改变拖船噪声源到第一个水听器的水平距离r，得到的仿真结果如表1所示。从表1中可以看出：当r逐渐增大时，偏离角Δθ和幅值差ΔP先逐渐减小再略有增大，Δθ的变化范围是10.1°～15.7°，变化范围较大，因此Δθ对r较为敏感；当r从600 m增大到1 200 m时，Δθ的变化量为5.6°，而当r从1 200 m增大到2 000 m时，Δθ的变化量却仅为0.2°。所以当r超过一个阈值后，对Δθ的影响变小。

表1 水平距离r变化时对应的Δθ、Pmax、P0、ΔPTable 1 The corresponding Δθ, Pmax, P0, ΔP when the horizontal distance r changes

再利用控制变量法，分别改变水听器的间距d和噪声源的频率f，得到的仿真结果如表2和表3所示。从表2和表3中可以看出：随着水听器间距d的增大，偏离角Δθ逐渐减小，Δθ的变化范围为11°～11.2°，变化量较小；随着拖船噪声源频率f的增大，Δθ也逐渐减小，变化范围为11.1°～16.5°；Pmax和P0随着d的增大逐渐减小，而随着f的增大先增大再减小；当d或f增大时，幅度差ΔP逐渐增大，这与d、f的增大会导致波束宽度变窄有关。

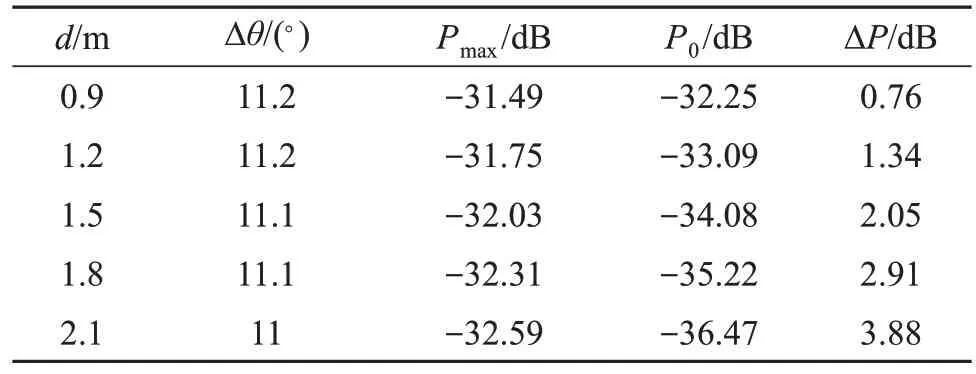
表2 水听器间距d变化时对应的Δθ、Pmax、P0、ΔPTable 2 The corresponding Δθ, Pmax, P0, ΔP when the hydrophone spacing d changes

表3 噪声源频率f变化时对应的Δθ、Pmax、P0、ΔPTable 3 The corresponding Δθ, Pmax, P0, ΔP when the frequency f of the noise changes

2.2.2 深海仿真结果

设置海深为2 000 m，拖船噪声源的频率为150 Hz，利用射线模型计算从拖船噪声源到第1个和第N个水听器的本征声线，结果如图5所示。从图5中可以看到，有多条到达接收点的本征声线，不同本征声线到达线列阵的入射角不同，但由于线列阵不能区分水平和垂直方向的来波信号，所以造成了线列阵对拖船自噪声波束响应偏离端射方向的现象。

图5 深海环境声传播的本征声线Fig.5 Eigen rays of sound propagation in the deep-sea environment

利用射线模型进行声场计算，模拟基阵接收到的拖船噪声信号，同样根据常规波束形成算法得到线列阵对拖船自噪声的波束响应。通过改变海深h3、线列阵深度h2、拖船噪声源到第一个水听器的水平距离r、拖船噪声源频率f，研究深海环境下的拖船干扰特性。

改变海深h3，得到的仿真结果如图6所示。从图6中可以看到，与浅海环境下得到的仿真结果不同，深海环境下，拖船自噪声除了在靠近端射的方向产生干扰外，还会在远离端射方向产生一个方位区间较大强度较高的干扰，后续主要对该干扰的特性进行分析。为便于描述，我们利用Pθ1，max表示远离端射干扰区间内的最大干扰幅度，其对应的方位角与端射方向的夹角为Δθ1。当海深由2 000 m逐渐增加到5 000 m，对应的Pθ1，max分别为-54.58、-57.92、-59.92、-64.57 dB，对应的偏离角Δθ1分别为72°、77°、80°、83°。所以随着海深的增加，偏离角Δθ1逐渐增大，干扰幅度Pθ1，max逐渐减小。同时在图6中可以看到，靠近端射方向干扰所对应的幅度几乎不变。根据式(4)，随着h3的增加，α和γ保持不变，β逐渐增大。所以深海环境下，远离端射方向的干扰主要由经海底反射后入射到基阵的声线造成，靠近端射方向的干扰与海底反射声关系不大。至于Pθ1，max随着h3的增加逐渐减小，则与海深的增加导致海底反射声的传播损失变大有关。

图6 改变海深时线列阵对拖船噪声波束响应的仿真结果Fig.6 Simulation results of the beam response of the linear array to the self-noise of tow-ship when changing ocean depths

再分别改变线列阵的深度h2、第一个水听器到拖船噪声源的水平距离r、拖船噪声源的频率f，得到的仿真结果如表4～6所示。从表4～6中可以得到如下结论：当海深不变，随着线列阵的深度h2的增加，偏离角Δθ1保持不变，对应的干扰幅度Pθ1，max先增大再减小；随着水平距离r的增加，偏离角Δθ1逐渐减小，干扰幅度Pθ1，max逐渐增加；随着拖船噪声源频率f的增大，偏离角Δθ1先减小再保持不变，干扰幅度Pθ1，max逐渐减小。根据式(8)，随着线列阵深度h2或者水平距离r的增大，β逐渐减小，但由于线列阵h2的深度变化范围相对较小，引起的方位角变化不明显，水平距离r的变化量相对较大，方位角的变化较明显，所以出现了表4和表5中的仿真结果。

表4 线列阵深度h2变化时对应的Δθ1、Pθ1，maxTable 4 The corresponding Δθ1, Pθ1，max when the depth h2 of the line array changes

表5 水平距离r变化时对应的Δθ1、Pθ1，maxTable 5 The corresponding Δθ1, Pθ1，max when the horizontal distance between tow-ship and line array r changes

表6 噪声源频率f变化时对应的Δθ1、Pθ1，maxTable 6 The corresponding Δθ1, Pθ1，max when the frequency f of the noise changes

2.3 深海仿真分析

本节主要利用仿真中得到的射线参数对深海环境下远离端射方向干扰出现的主要原因进行分析。深海环境下远离端射方向干扰产生的原因与线列阵对拖船自噪声的波束响应偏离端射方向的原因一样，也是由于海洋声信道的多途传播特性以及线列阵不能区分水平方向和垂直方向来波信号造成的。

现以图6中海深2 000 m和海深3 000 m时线列阵中心水听器接收到的声线参数为例，说明远离端射方向干扰出现的主要原因，具体参数如表7所示。表7中Narr表示基阵接收到的声线总数，ψ表示声线入射到基阵的角度范围，Narr1表示基阵接收到的直达声线数，Narr2表示基阵接收到的一次海面反射声线数，Narr3表示基阵接收到的一次海底反射声线数，φ1、φ2和φ3分别表示其对应的入射到基阵的角度(声线指向海底时角度为正值)。

表7 线列阵中心水听器接收到的拖船噪声所对应的声线参数Table 7 Sound ray parameters corresponding to the tow-ship noise received by the hydrophone at the center of the line array

由于入射到线列阵的声线较多，并且深海环境下经多次海面海底反射后造成的能量损失很大，因此在表7中，仅列出直达声、经一次海面和一次海底反射后入射到线列阵的声线。根据深海仿真结果可知，经海底反射后入射到线列阵的声线是造成远离端射方向干扰的主要原因。由表7可以看到，仿真中得到的靠近端射方向的干扰角度在φ1和φ2中能够找到近似值，而远离端射方向的干扰角度在φ2和φ3中能够找到近似值，并且φ2中与远离端射方向干扰角相近的角度在φ3中都能找到。这说明这些重合的角度是经过一次海底和一次海面反射后入射到线列阵的，而φ3中包含的所有角度都与远离端射方向干扰角相近。所以深海环境下，海底反射声确实是远离端射方向干扰出现的主要原因，直达声和海面反射声则是靠近端射方向干扰出现的主要原因。

3 海试结果分析

某海域不同海深时的海试数据处理结果如图7所示。图7(a)中远离端射方向的干扰与目标信号的可区分度较高，通过对靠近端射方向干扰和非端射方向干扰进行谱分析和相关性分析来进一步验证非端射方向的干扰来源。取300 s时14°和61°方位干扰波束数据，其对应的频谱如图8所示。

图7 不同海深时的海试数据时间方位历程图Fig.7 Time azimuth history charts of sea trial data at different depths

图8 不同方位的干扰波束频谱图Fig.8 Interfering beam spectrograms at different azimuths

从图8中可以看到，靠近端射方向的干扰波束会在频率为117、155、246、258、260、352、466、492、516、520 Hz有相应的线谱；远离端射方向的干扰波束会在频率为118、155、246、258、260、466、492、516、520 Hz时有相应的线谱。不同干扰波束对应频点上线谱幅度大小有差异。这与海洋声信道的传播特性有关，但可以发现两者所包含的线谱结构高度相似。再进行相关性分析，首先利用图8中的线谱挑选对应的处理频段，接着对靠近端射方向和非端射方向时域干扰波束做互相关，把互相关峰值对应的时延差作为非端射方向时域干扰波束的时延补偿值，然后计算两者的相关性，计算结果如下：处理频带为110～160 Hz时，相关系数为0.728；处理频带为240～270 Hz时，相关系数为0.716 6；处理频带为460～520 Hz时，相关系数为0.587 5；处理频带为110～120 Hz时，相关系数为0.917 8；处理频带为250～260 Hz时，相关系数为0.866 2。通过谱分析和相关系数的分析，可以验证靠近端射方向干扰和远离端射方向干扰都是由拖船自噪声引起的。

利用图7(b)来验证仿真实验以及说明远离端射方向干扰对目标信号检测的影响。先设置与当时试验环境相近的仿真参数，得到线列阵对拖船自噪声波束响应的仿真结果，如图9所示。

图9 试验环境相近的线列阵对拖船噪声波束响应的仿真结果Fig.9 Simulation results of the beam response of the linear array to the self-noise of tow-ship in the similar experimental environment

从图7(b)中可以看出，远离端射方向的拖船干扰会出现在60°～80°方位区间内，而从图9仿真结果中可以发现，拖船自噪声会在77°方位产生一个干扰峰，所以仿真结果与海试数据处理结果一致。从图7(b)中还可以看到，300 s以前，在方位角81°左右存在目标信号，但随着目标的移动，当其位于干扰区间内，由于受到拖船干扰的影响，在400 s以后无法有效识别出目标信号。这表明60°～80°方位区间内的拖船干扰确实会影响远场目标信号的方位识别和拖曳声呐的探测性能。

4 结 论

本文研究了拖曳声呐在不同环境下对拖船自噪声的波束响应。仿真结果表明，浅海和深海环境下拖船自噪声都会在偏离端射较近的方向产生干扰，而深海环境下拖船自噪声还会在远离端射方向产生干扰，该干扰存在的方位区间和强度较大，主要是由经海底反射后入射到线列阵的声线引起的。拖船干扰的强度以及其对应的方位角与海深、线列阵深度、拖船噪声源深度、水听器到拖船噪声源的水平距离、拖船噪声源频率以及水听器之间的间距有关。深海环境下，拖船自噪声引起的远离端射方向干扰主要与海深和水平距离有关，随着海深的增加或水平距离的减小，远离端射方向干扰方位角不断增大，对应的干扰强度逐渐减小，方位角的变化规律与根据几何关系得到的海底反射声入射角的变化规律较吻合。海试数据处理结果表明，深海环境下，出现的远离端射方向干扰与靠近端射方向的干扰都是由拖船自噪声造成，并且远离端射方向干扰会对拖曳声呐的探测性能产生较大影响。通过分析线列阵在不同环境下对拖船自噪声的波束响应，可以为拖船自噪声抑制算法的研究提供理论依据，后续还可以考虑利用深海环境下远离端射方向干扰的特性开展相关应用。