反潜巡逻机声呐浮标巡逻搜索态势分析模型
谭安胜, 王新为, 尹成义
(海军大连舰艇学院舰船指挥系,辽宁 大连 116018)
0 引言
反潜巡逻机在巡逻线上对潜搜索,简称巡逻搜索。巡逻搜索是指为了阻止敌潜艇通过某海域而进行的反潜活动。在实施这种反潜活动时,反潜巡逻机在垂直于已查明或预计的敌潜艇航线的带状海域实施对潜搜索。反潜巡逻线通常设置在:1)狭窄海域、水道;2)敌潜艇向战斗海区展开的航路上;3)为了警戒已搜索过的海域;4)反潜兵力数量无法满足搜索全部的敌潜艇可能机动的海域;5)为己方潜艇的活动海区实施反潜保障;6)为己方某作战海区实施反潜警戒。反潜巡逻机在巡逻线上进行搜索时,可使用的搜索器材主要包括声呐浮标和磁探仪。反潜巡逻机使用声呐浮标在巡逻线上搜索时,通常布设声呐浮标线型阵(简称“线型阵”或“线列阵”)。线列阵中浮标的数量和相邻浮标之间的间距,取决于要求的目标发现概率、声呐浮标作用距离以及作战海区环境等条件[1-6]。
1 基本假设与建模准备
反潜巡逻机为了阻止敌潜艇通过某海域,在其必经或可能的展开航路上设置巡逻线,并在巡逻线上使用声呐浮标布设线列阵,形成阻塞式障碍。为了实施对潜艇的搜索,必须布设和监听线列阵。所以在研究使用声呐浮标进行巡逻搜索问题时,必须综合一体考虑布设线列阵、监听线列阵以及布阵与听阵之间的关系。
1.1 基本假设
1) 敌潜艇的主航向垂直于线列阵方向;2) 敌潜艇等概率地从线列阵上的任意一点突破;3) 线列阵中所有浮标都处于值班工作状态;4) 声呐浮标(简称“浮标”)总是以线列阵的形式使用,线列阵由被动全向声呐浮标组成,且各枚浮标性能相同;5) 不考虑海况(风、流)对浮标投放和落点位置的影响。
1.2 建模准备
根据基本假设,在敌潜艇可能的展开航路上布设一道或数道线列阵。如图1所示,在敌潜艇展开航路上布设了两道线列阵,记为FZ(L2)。若布设了n道线列阵,则记为FZ(Ln)。为了研究方便,将一道线列阵称为“单列阵”,记为FZ(L1);将两道和两道以上的线列阵称为“复列阵”,依次记为FZ(L2),FZ(L3),…,FZ(Ln)。
敌潜艇要想隐蔽通过线列阵障碍,可能采用以下方法:1) 利用最小噪音的最大航速从线列阵中的两个浮标之间通过;2) 绕过线列阵,从线列阵的两端通过;3) 加大潜航深度,隐蔽通过。
显然,针对敌潜艇突破线列阵障碍的可能行动方法,需要研究解决下列基本问题:1) 布设几道线列阵,线列阵之间的间距为多少?2) 线列阵内浮标之间的间距多少,线列阵的长度多少?3) 如何布设和监听,布设和监听之间的关系如何?而上述基本问题,又取决于要求的发现概率、声呐浮标作用距离、反潜巡逻机的最大巡逻时间、可用反潜巡逻机的数量、一架反潜巡逻机的浮标携带量以及作战海区环境等条件因素。为此,必须综合考虑。
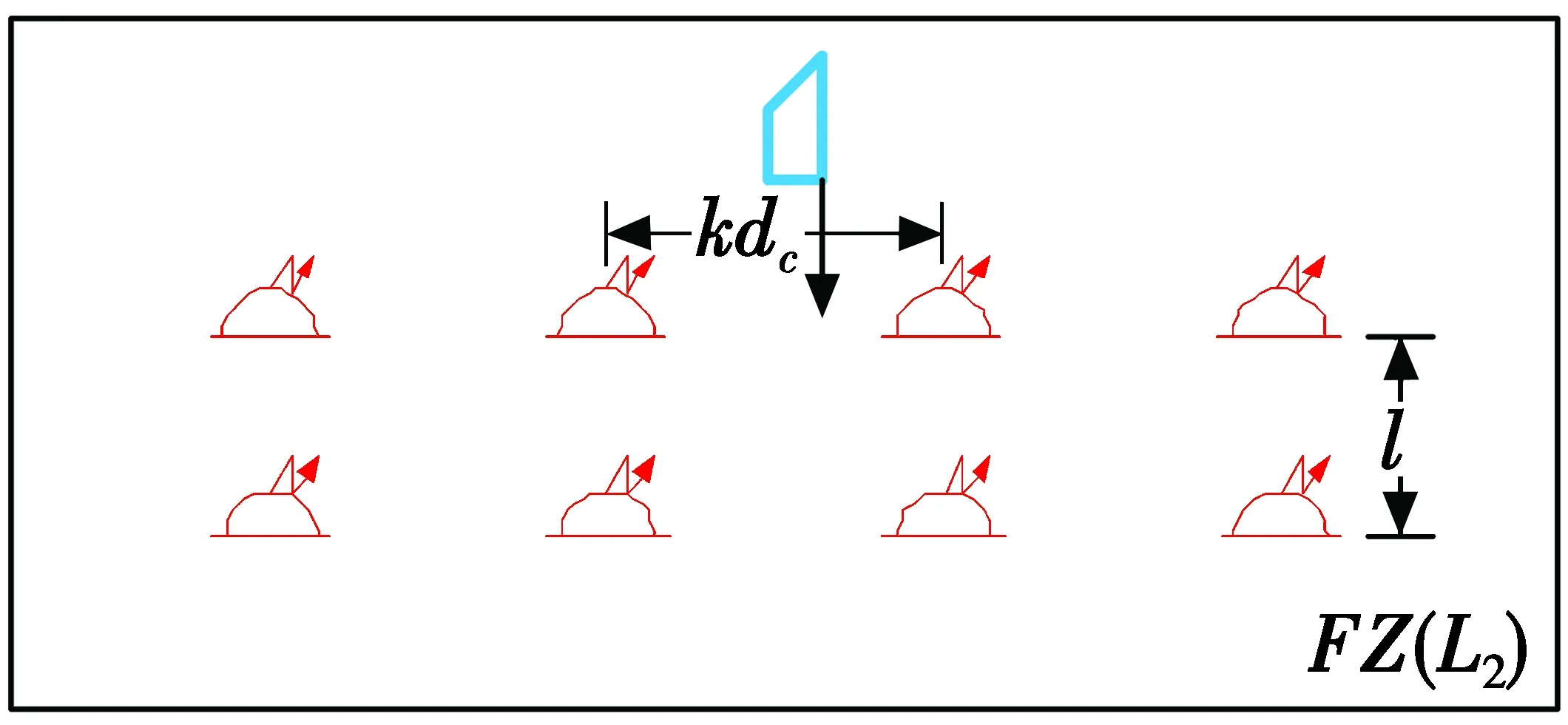
图1 线列阵态势分析示意图Fig.1 Schematic diagram of linear array situation analysis
2 单列阵搜索态势分析模型
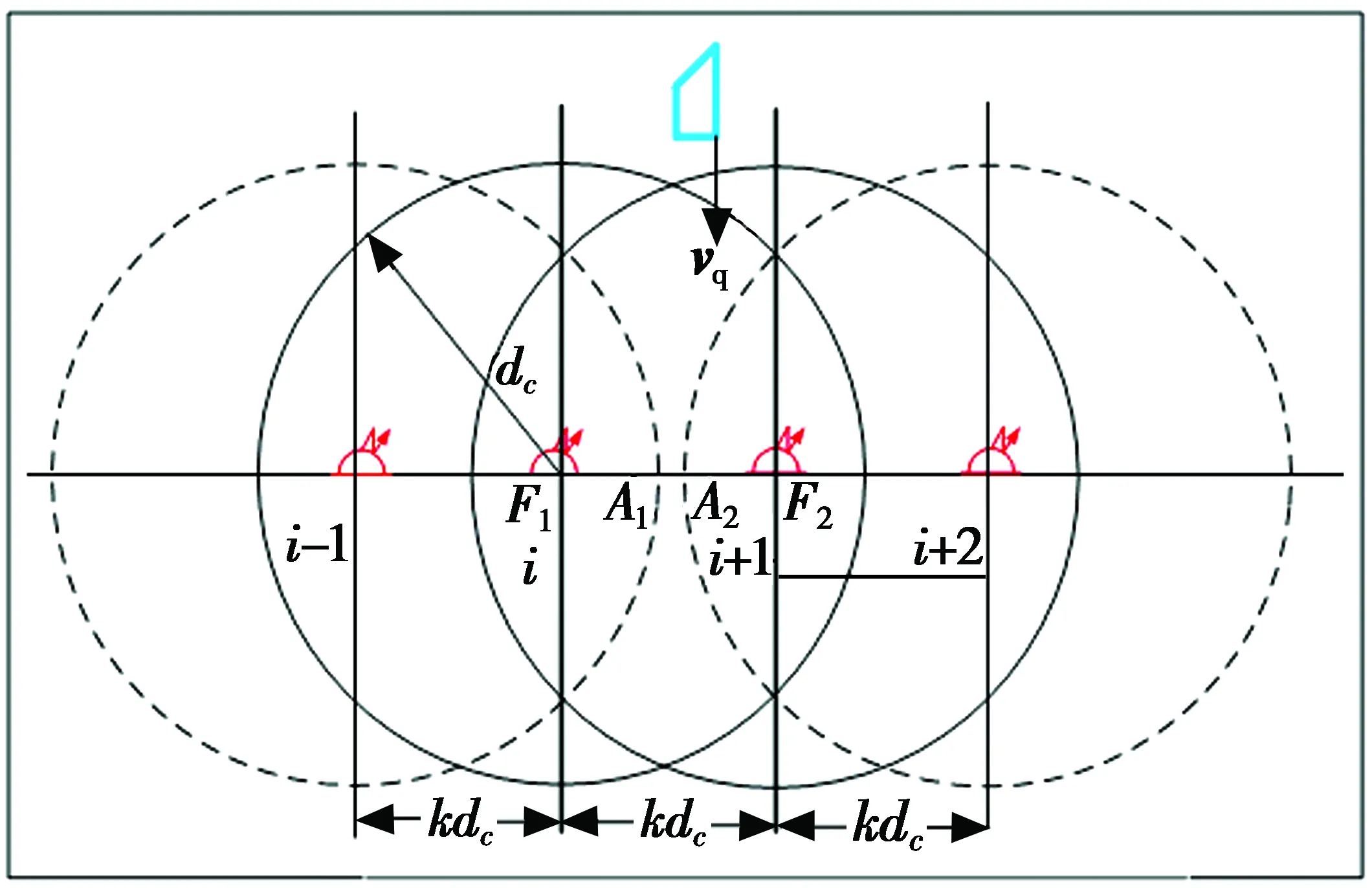
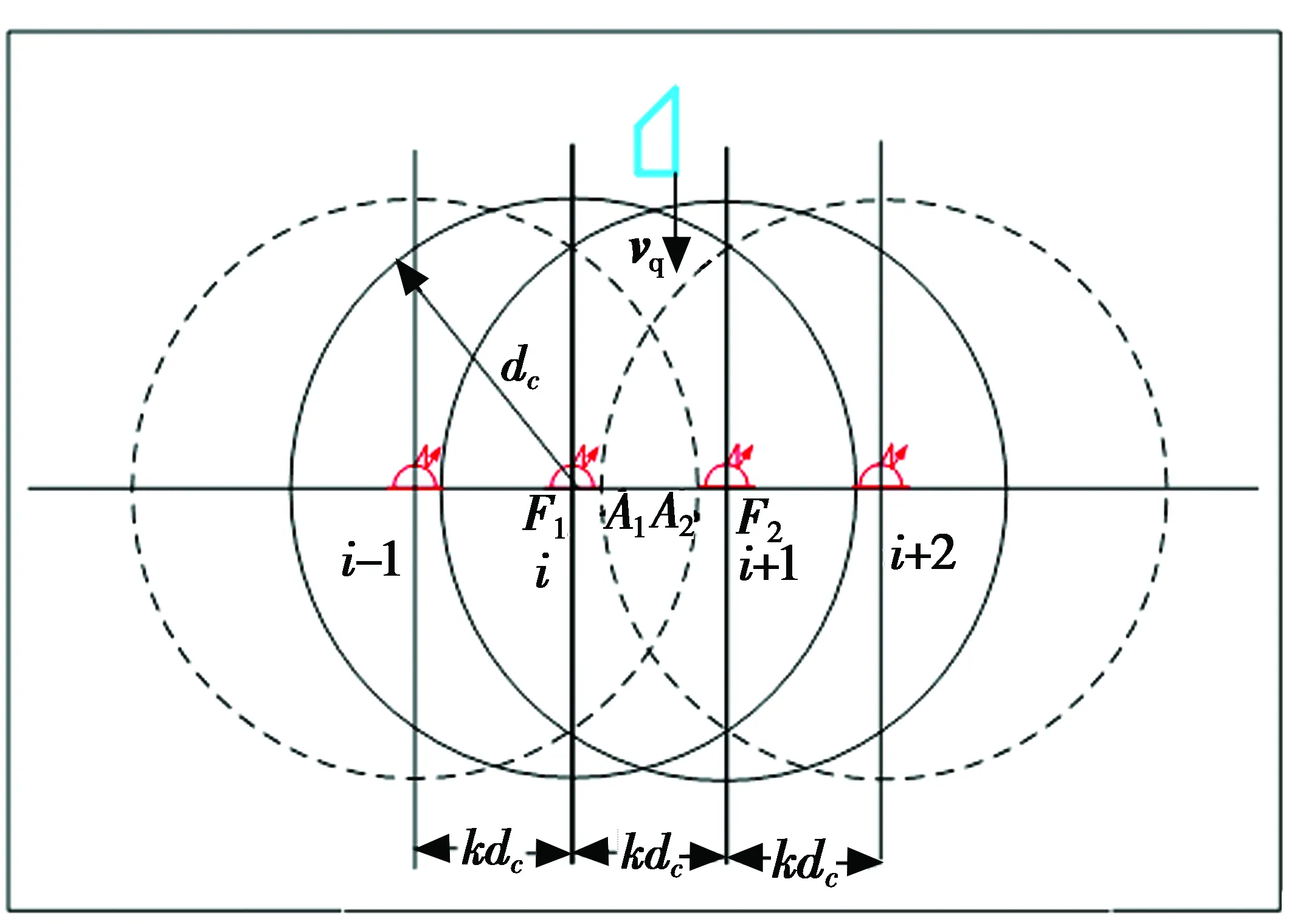
如图2所示,在单列阵(或称“线列阵FZ(L1)”)中,第i枚与第i+1枚浮标分别位于F1,F2点。
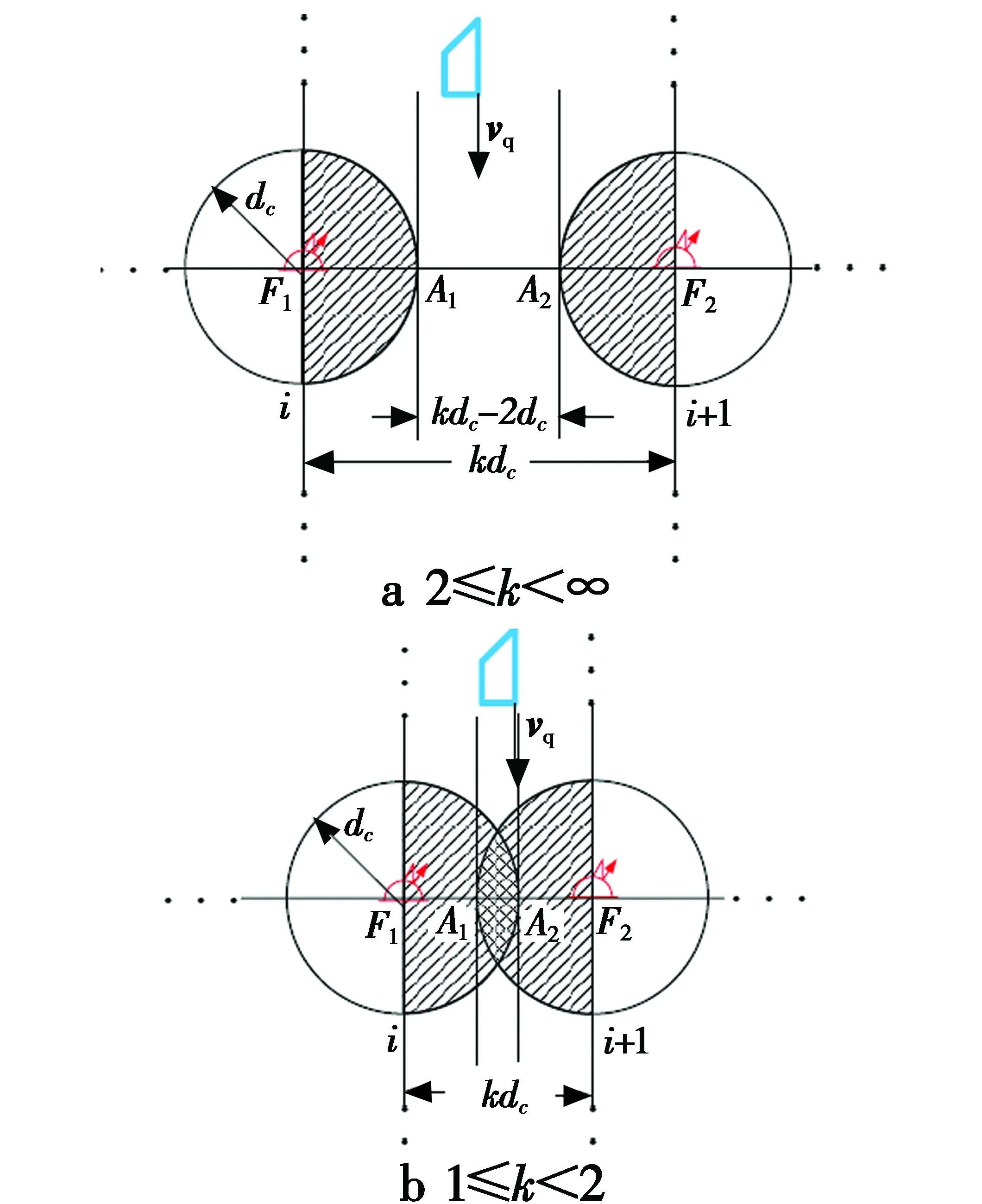
图2 单列阵态势分析示意图
Fig.2Single linear array situation analysis
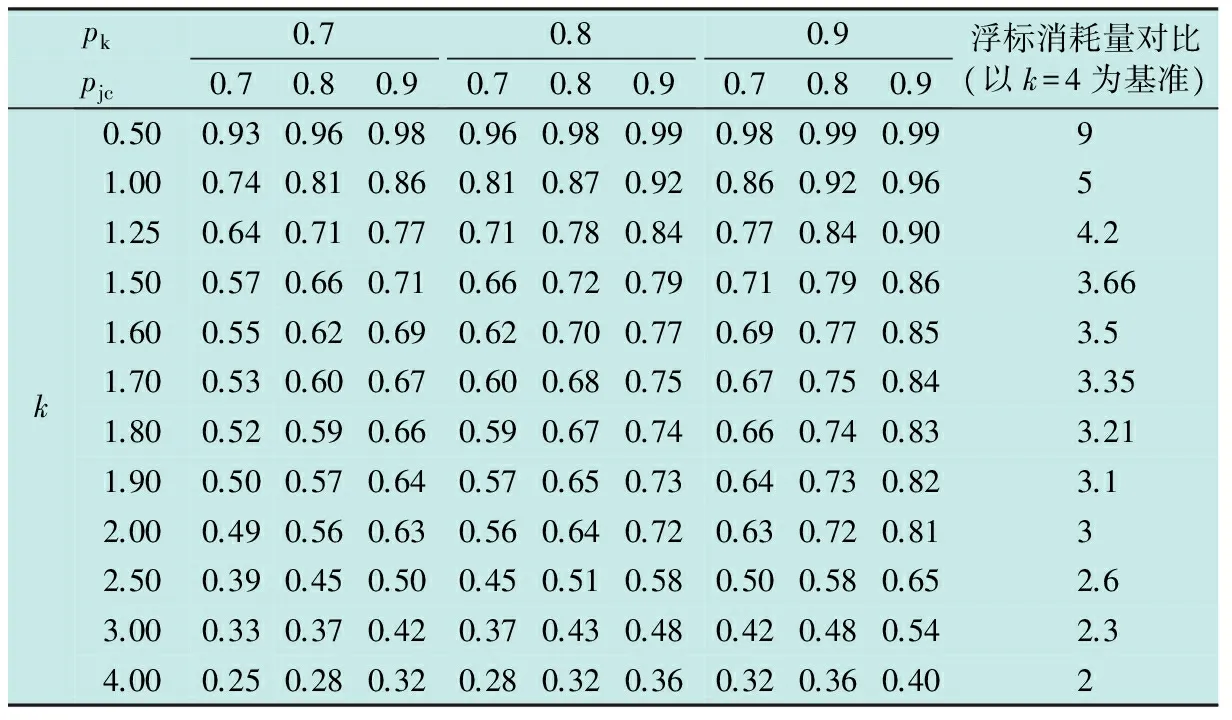
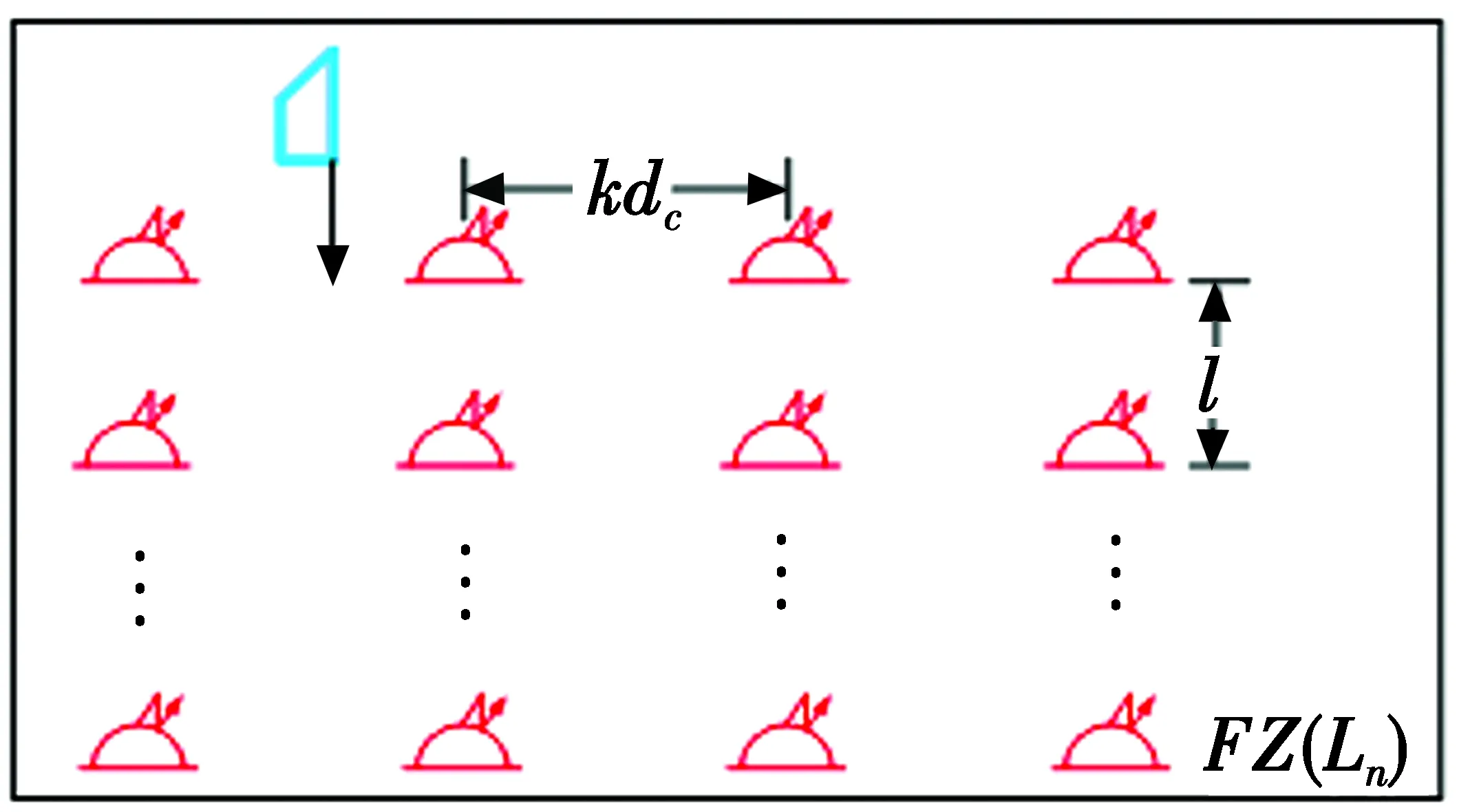
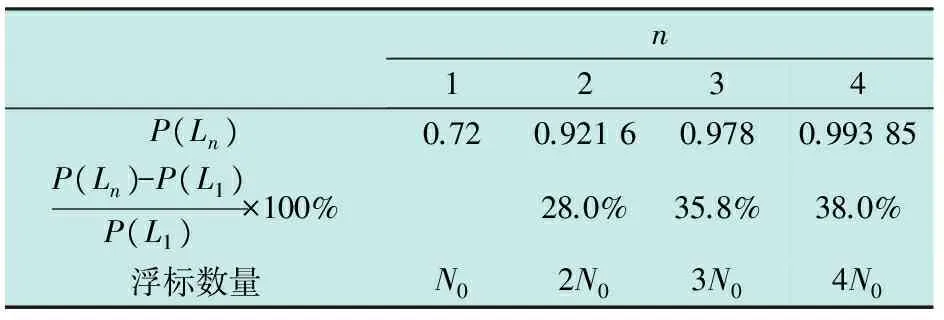
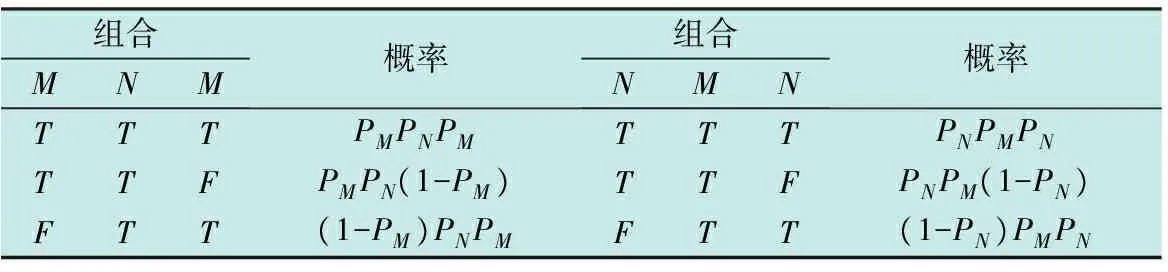
设声呐浮标的有效探测距离为dc,线列阵FZ(L1)中任意相邻的第i枚与第i+1枚浮标之间的间距为kdc,0 如图2a所示,当敌潜艇从A1A2段穿越线列阵FZ(L1)时,潜艇不被发现;当敌潜艇从线列阵FZ(L1)中的F1A1或A2F2段穿越时,将进入声呐浮标的作用范围。设任意一枚浮标的接触概率相同均为pjc,浮标入水后可靠工作的概率为pk,则线列阵FZ(L1)发现潜艇的概率PL为 (1) 如图2b所示,如果潜艇进入线列阵FZ(L1)中的F1A1或A2F2段时,将进入第i枚或第i+1枚浮标的作用范围,此时发现潜艇的概率为 (2) 表1 假设和发现概率(2/3≤k<1) 如果潜艇进入线列阵FZ(L1)中的A1A2段时,将同时进入第i枚和第i+1枚浮标的共同作用区内,此时发现潜艇的概率为 (3) 则,线列阵FZ(L1)发现潜艇的全概率为 (4) 此时有多种情况,为不失一般性,本文选两种典型情况进行讨论。 2.3.1当2/3≤k<1时 如图3所示,如果潜艇进入线列阵FZ(L1)中的F1A1段时,将进入第i-1枚、第i枚、第i+1枚浮标的作用范围;如果潜艇进入线列阵FZ(L1)中的A2F2段时,将进入第i枚、第i+1枚、第i+2枚浮标的作用范围;如果潜艇进入线列阵FZ(L1)中的A1A2段时,将进入第i枚、第i+1枚浮标的作用范围。设任意一枚浮标的接触概率相同均为pjc,浮标入水后可靠工作的概率为pk,则这些假设和发现概率如表1所示。 因此,发现潜艇的全概率由 (5) 确定。 图3 单列阵态势分析示意图(2/3≤k<1) 2.3.2当0.5≤k<2/3时 如图4所示,如果潜艇进入线列阵FZ(L1)中的F1A1段时,将进入第i-1枚、第i枚、第i+1枚浮标的作用范围;如果潜艇进入线列阵FZ(L1)中的A2F2段时,将进入第i枚、第i+1枚、第i+2枚浮标的作用范围;如果潜艇进入线列阵FZ(L1)中的A1A2段时,将进入第i-1枚、第i枚、第i+1枚、第i+2枚浮标的作用范围。设任意一枚浮标的接触概率相同均为pjc,浮标入水后可靠工作的概率为pk,则这些假设和发现概率见表2。 表2 假设和发现概率(0.5≤k<2/3) 表3 单列阵发现潜艇的概率(dc=2 km) 因此,发现潜艇的全概率由 (6) 确定。 综合上述情况,线列阵FZ(L1)发现潜艇概率可表示为 (7) 整理得 (8) 由此可得,不同浮标间距下,单列阵发现目标概率通式为 (9) 从表3可以看出:1) 在确定的浮标有效作用距离下,相邻浮标之间的间距、 接触概率和浮标完好率,决定了线列阵FZ(L1)发现目标概率的大小;2)k=1与k=0.5相比,发现概率最大增加了25.6%,最小只增加了3.1%,而浮标消耗量增加了80%。可见,当k<1时,浮标消耗量将急剧增加,而发现概率的增加并不明显。因此,在实际作战与训练中一般不应采用k<1的情况。 图4 单列阵态势分析示意图(0.5≤k<2/3) 如果在敌潜艇必经或可能的展开航路上设置多道线列阵(垂直于目标航向),比如设置n道线列阵,记为复列阵FZ(Ln),如图5所示,以考察这种情况下对目标的搜索效能。 图5 多层线列阵搜索态势分析示意图 (10) P(Ln)=1-(1-PL)n (11) 设n=4,且每道线列阵具有相同的结构(k=1.5);令pk=0.8,pjc=0.8。查表3,应用式(11)计算P(Ln)随n的变化规律,以及P(Ln)的增量ΔP(Ln)随n的变化规律,如表4所示。 表4 P(Ln)以及ΔP(Ln)随n的变化规律 从表4可以看出,复列阵FZ(Ln)中的线列阵由1道增加到2道时,发现目标的概率增加了28%,浮标量增加至2倍;由1道增加至3道时,发现目标的概率增加了35.8%,浮标量增加至3倍;由1道增加到4道时,发现目标的概率增加了38%,浮标量增加至4倍。由此可得出如下结论:在实际作战中,为提高搜索效率,巡逻搜索时复列阵FZ(Ln)可以由2~3道线列阵组成。若线列阵数量再增加,发现潜艇的概率增加的并不明显,而浮标的消耗量却成倍增加。通常情况下,以两道线列阵组成复列阵为佳,最多不宜超过3道。 在组织巡逻搜索时,为了提高搜索中发现目标的概率和(或)得到目标通过巡逻线的运动方向,可以采用线列阵梯次配置形成复列阵的搜索方法。可以认为,至少有连续两次发现目标就可以确定目标通过巡逻线的运动方向。例如在第1道和第2道巡逻线上发现,或第2道和第3道巡逻线上发现。 假设线列阵梯次配置搜索的目的是确保至少有连续两次发现目标,从而确定目标的运动方向。当设置3个梯次配置的线列阵时,如果3个线列阵结构完全一致,即发现目标的概率都一样,那么无论以何种组合来分层梯次配置都可以。 现在假定有两种结构不同的线列阵M,N,即kMdc≠kNdc,其发现目标的概率分别为PM,PN,且PM>PN。令T,F分别代表发现目标事件和未发现目标事件,P代表发现概率的总值。假定目标的发现是独立的,则反潜巡逻机在复列阵“M-N-M”和“N-M-N”上,至少连续两次发现目标的每种组合的结果及其概率列于表5中。在给定组合下至少有连续两次发现的概率和发现数的数学期望列于表6中。 表5 复列阵不同配置方法及其发现概率 表6 在给定组合下至少两次连续发现概率、发现数的数学期望 因为 (12) 所以 (13) 现用具体数据来比较:设pk=0.8,pjc=0.8,则M(kM=1.5)结构类型的线列阵发现目标的概率为PM=0.72(查表3),N(kN=2.5)结构类型的线列阵发现目标的概率为PN=0.51(查表3),则有“M-N-M”组合,PMNM=PMPN(2-PM)=0.470,EMNM=2PM+PN=1.95;“N-M-N”组合,PNMN=PMPN(2-PN)=0.547,ENMN=2PN+PM=1.74。 从计算结果可以看出: 1) 至少连续两次发现目标的概率PNMN,大于第2道线上为N结构类型的线列阵发现目标的概率PMNM,也就是说,按“N-M-N”结构来配置复列阵是合适的; 2)PMNM 通过上述分析,得出如下结论。 1) 巡逻搜索时复列阵可以由2~3道线列阵组成,最多不宜超过3道; 2) 在实际作战中,为了提高搜索效率,巡逻搜索时复列阵通常应由两道线列阵组成; 3) 两道线列阵最好具有相同的结构,若为了减少浮标的消耗量而采用不同的结构,最好按“N-M”模式来配置复列阵,也就是说,将浮标密度小的线列阵布设在内侧,而将浮标密度大的线列阵布设在外侧; 4) 两道线列阵组成的复列阵之间的距离要保证,反潜巡逻机飞至处于另一道发出信号浮标上空的时间不大于潜艇穿越复列阵间距的时间,即l≥DTX·vq/va,DTX为反潜巡逻机与浮标的通信距离,va,vq分别为反潜巡逻机和潜艇的速度。 研究反潜巡逻机巡逻搜索方法,需要综合考虑一架反潜巡逻机的布阵能力、监听能力以及布阵与听阵之间的关系。巡逻搜索方法的本质就是将搜索兵力(反潜巡逻机)与搜索兵力的能力(布设与监听线列阵的最大长度)在给定巡逻线上的时空安排。 如图6所示,反潜巡逻机在垂直于已查明或预计的敌潜艇航线的带状海域设置巡逻线Lxl实施对潜搜索。根据1.1节中基本假设2),3),敌潜艇从巡逻线Lxl上的任意点突破是等概率的。所以,要想及时发现突破巡逻线Lxl的敌潜艇,必须在巡逻线Lxl上布设浮标,形成线列阵障碍。线列阵障碍中所有浮标都必须同时处于值班工作状态。也就是说,只有当线列阵障碍中的所有浮标都同时处于值班工作状态时,线列阵障碍才具有真正意义上的封闭性。 假设一架反潜巡逻机能够布设并监听的线列阵的最大长度为L(标准线列阵)。那么,对于给定长度为Lxl的巡逻线,当Lxl>L时,则需要Lxl/L架反潜巡逻机才能实现对巡逻线的封闭;当Lxl≤L时,则一架反潜巡逻机即可完成任务。因此,当Lxl>L时,可将巡逻线Lxl划分成几个“巡逻段”(或称为“浮标段”),其长度为LD。每个巡逻段(浮标段)的长度LD不超过一个标准线列阵的长度L,即LD≤L。一个标准线列阵由一架反潜巡逻机布设和监听浮标的能力决定。 图6 巡逻搜索方法分析示意图Fig.6 Schematic diagram of patrol search method 显然,搜索方法的研究要解决两大问题:1) 单架反潜巡逻机布设和监听线列阵的方法;2) 多架反潜巡逻机布设和监听线列阵的方法。第1个问题是解决第2个问题的基础。 针对第1个问题,即当Lxl≤L时,根据布设浮标与监听浮标之间的关系,分两种情况讨论(参考图6)。 1) 某架反潜巡逻机从a点开始布设浮标,浮标工作时间为tc,布设至b点时其线列阵的长度LD≤L,所用的布阵时间为tbz,且有tbz 2) 某架反潜巡逻机从a点开始布设浮标,布设浮标的过程中就开始对已布设的浮标进行监听。布设至b点时其线列阵的长度LD≤L,浮标工作时间为tc,所用的布阵时间为tbz,且有tbz 针对第2个问题,即当Lxl>L时,可根据多架反潜巡逻机组成的战术编队在布设线列阵时的协同方式分两种情况讨论。 1) 如果战术编队中各架反潜巡逻机,同时在各自分配的巡逻段LD≤L上布设浮标,则称这种布阵方法为“同时法”。 2) 如果战术编队中各架反潜巡逻机,依次在各自分配的巡逻段LD≤L上布设浮标,则称这种布阵方法为“依次法”。 综合上述分析,反潜巡逻机在巡逻线上的搜索方法可分为:1) 当Lxl≤L时,单机布听同步巡逻搜索法、单机布听异步巡逻搜索法;2) 当Lxl>L时,多机分段同时布听同步巡逻搜索法、多机分段依次布听同步巡逻搜索法;多机分段同时布听异步巡逻搜索法、多机分段依次布听异步巡逻搜索法。如果考虑到反潜巡逻机在监听时采用不同的监听轨道,也可将采用的监听轨道元素置于搜索方法的命名中。 综合上述搜索态势和搜索方法的研究结果,得出如下结论: 1) 巡逻搜索时,巡逻线的位置和长度应当由上级根据作战企图决定; 2) 为了在上级指定的巡逻线搜索敌潜艇,反潜巡逻机通过布设线列阵实施; 3) 线列阵中浮标的数量和相邻浮标的间距取决于要求的发现概率、浮标发现潜艇的距离和搜索条件; 4) 在确定一架反潜巡逻机能够布设的线列阵长度时,需要考虑所携带的浮标数量和在巡逻线上的留空时间; 5) 当根据战术意图确定的巡逻线的长度L很长时,应将巡逻线划分成几个“巡逻段”,每个巡逻段的长度LD由一架反潜巡逻机布设和监听浮标的能力决定,且LD≤L; 6) 为使敌方难以查明线列阵的位置,在各“巡逻段”上应当使用不同的监听轨道; 7) 为在巡逻线上布设线列阵,应确定每个“巡逻段”上的浮标开始和结束布设点坐标、浮标间距和数量;或者确定每个“巡逻段”上的浮标开始布设点坐标、线列阵方位、浮标间距和数量; 8) 线列阵的形状(单列阵或复列阵)由指挥员根据战术意图确定。为了提高搜索效率和(或)测出敌潜艇的运动要素,可选择由2~3道单列阵组成的复列阵; 9) 如果浮标工作时间小于反潜巡逻机在巡逻线的留空时间,且还没有达到上级要求的持续监听时间,若还有足够的浮标,反潜巡逻机可再次布设线列阵; 10) 如果浮标的工作时间长于反潜巡逻机在巡逻线上的留空时间,且还没有达到上级要求的持续监听时间,应当组织反潜巡逻机实施换班监听; 11) 如果反潜巡逻机的留空时间有限,布阵与听阵的反潜巡逻机可以由不同批次的反潜巡逻机来执行; 12) 研究反潜巡逻机巡逻线搜索方法,需要综合考虑一架反潜巡逻机的布阵能力、监听能力以及布阵与听阵之间的关系。 这12条综合结论,既是反潜巡逻机使用声呐浮标对潜巡逻搜索时的组织实施要点,又为反潜巡逻机使用声呐浮标进行巡逻搜索提供了理论与技术基础。关于本文提到的标准线列阵及其布阵方法等问题,将在后续文章中介绍。 [1]张最良,李长生,赵文志,等.军事运筹学[M].北京:军事科学出版社,1993. [2]孙明太.航空反潜装备[M].北京:国防工业出版社,2012. [3]谭安胜.水面舰艇编队作战运筹分析[M].北京:国防工业出版社,2009. [4]谭安胜.反潜巡逻机声呐浮标区域搜索研究—布听同步搜索[J].电光与控制,2017,24(5):1-9. [5]谭安胜.反潜巡逻机声呐浮标区域搜索研究—布听异步搜索[J].电光与控制,2017,24(6):1-9. [6]曲也频.反潜飞机搜潜效能评估与决策建模[M].北京:国防工业出版社,2011.2.1 当2≤k<∞时
2.2 当1≤k<2时
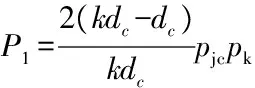

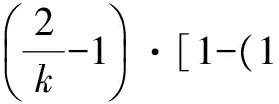
2.3 当0


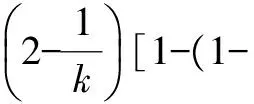
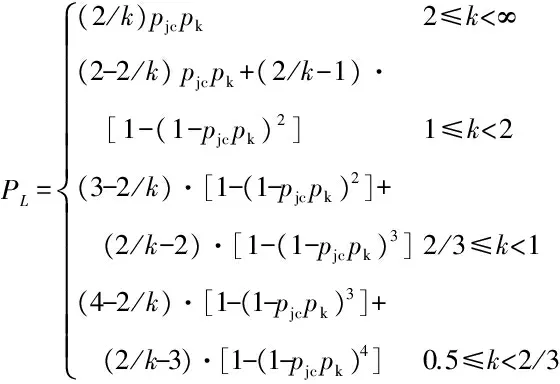


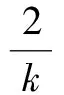
3 复列阵搜索态势与配置分析模型
3.1 复列阵搜索态势分析模型
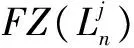
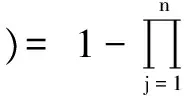
3.2 复列阵配置分析模型
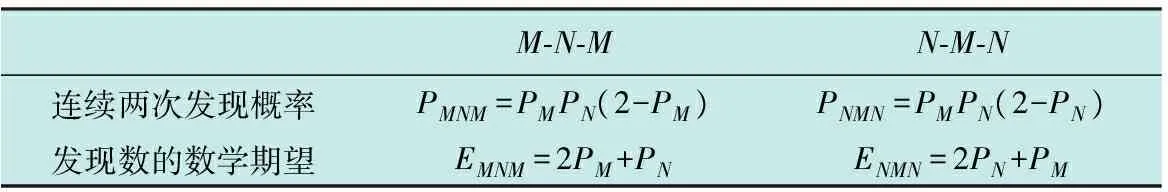
4 巡逻搜索方法分析模型

5 综合结论

