基于模糊控制的倾转三旋翼无人机过渡模式操纵策略研究

张　飞，　路　平，　江　涛，　史凤鸣

(陆军工程大学无人机工程系，石家庄　050003)

0　引言

倾转三旋翼无人机作为可垂直起降固定翼飞行器的一种，它具有直升机垂直起降、定点悬停的功能，又能像固定翼飞行器高速续航飞行，很好地解决了固定翼飞行器对起降环境要求高和直升机速度低、航程短的短板，在未来的军用和民用领域均具有广阔的应用前景。

然而，在倾转三旋翼飞行器飞行性能大幅度提高的同时，也面临着控制难度增大的问题。倾转三旋翼飞行器具有3种飞行模式：满足垂直起降和悬停、低速前飞的直升机模式、高速巡航飞行的固定翼模式以及在直升机模式和固定翼模式之间相互切换的过渡模式。为了满足倾转三旋翼无人机飞行过程控制需求，其同时配备了直升机和固定翼飞行器的操纵系统。然而，在过渡模式中，由于增加了发动机短舱倾转这个操纵量，两套控制方案均不适用于单独使用，需要一套合适的过渡模式下的操纵策略来解决其面临的操纵冗余问题。

国外对倾转旋翼机的研究开展较早，针对飞行过程中的气动特性、旋翼/机翼相互耦合干扰已经取得了一系列的理论成果[1-4]以及以V-22鱼鹰倾转旋翼机为代表的实际成果，而国内研究则开展较晚。文献[5]对倾转三旋翼飞行器近地悬停以及低速前飞过程中的地面效应展开了研究；文献[6]建立了倾转旋翼飞行器过渡模式模型，在Maltab仿真环境下对其进行了配平分析；文献[7]利用最优方法对倾转旋翼飞行器在不同飞行模式下进行了配平分析。

本文针对倾转三旋翼无人机过渡模式中的操纵冗余度问题，建立了合适的倾转三旋翼过渡模式动力模型，将其倾转过程分为两个阶段，基于模糊控制理论，利用倾转过程中飞行器纵向高度变化和俯仰角对发动机短舱倾转速度进行控制，以达到对倾转旋翼飞行器倾转过程稳定控制，使飞行器平稳过渡的目的。

1　倾转三旋翼无人机数学模型

倾转三旋翼无人机气动力模型包括左/右旋翼、尾部旋翼、机翼、机身、平尾、垂尾、升降舵和方向舵。本文建模对象倾转三旋翼无人机采用正三角形布局，飞行器的质心与形心重合，其机体轴系原点位于飞行器质心，坐标轴系如图1所示。

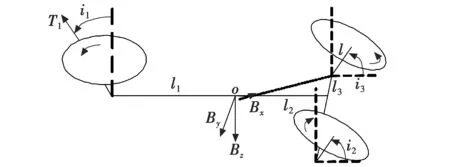
图1　倾转三旋翼无人机机体坐标系示意图Fig.1　Tilt tri-rotor UAV body coordinate system

Eb=[Bx,By,Bz]为机体坐标系，原点o位于机体重心，其中，Bx指向机头方向,By指向机身右方,Bz垂直于机身向下。i1为尾部旋翼为抵消自身扭转力矩所偏转的角度，i2，i3为前置旋翼在过渡模式下发动机短舱倾转过程中所倾转的角度，其中，设直升机模式下i2=i3=90°，固定翼模式下为0°。

1.1　旋翼模型

倾转三旋翼无人机具有3副旋翼，其中，前置旋翼2，3关于xoz平面对称，为了方便，设旋翼倾转角度为in，其中i2=i3。则旋翼数学模型为

(1)

式中：Tln为旋翼对空气做功所产生的拉力；Dn为空气对旋翼产生阻力；Tn为旋翼产生的升力；τn为旋翼自身旋转所产生的扭力；wn，R，S，ρ分别为旋翼转速、旋翼半径、桨盘面积和空气密度；c1，c2，c3分别为旋翼拉力系数、阻力系数和扭力系数，与旋翼迎风速度有关，可通过实验方式测得。旋翼1为了平衡自身扭转力矩，需满足

T1sini1=τ1。

(2)

旋翼2和旋翼3旋转方向相反。

当飞行器平飞速度为υ，机体滚转角、俯仰角和偏航角分别为φ，θ，ψ，规定分别以右滚转、抬头和右偏为正方向。经过欧拉转换后的质心运动速度为[υx,υy,υz],则旋翼1桨毂中心速度为

(3)

旋翼2、旋翼3桨毂中心速度为

(4)

左右旋翼的区别在于转向相反，当飞行条件相同时，为简化计算模型，认为左右旋翼扭转力矩相互抵消。根据直升机飞行动力学理论[8]，可通过桨毂中心速度，得到旋翼前进比u

(5)

及采用牛顿迭代法求得的入流比λ

(6)

1.2　机翼模型

对倾转旋翼飞行器来说，在其过渡模式下，随着发动机短舱角的变化，机翼的气动力模型非常复杂，因为机翼上气流不仅与发动机短舱角度相关，还随着飞行器飞行速度的变换呈复杂非线性变化。本文对机翼进行建模分析，为了方便计算，将机翼气动力模型分为两个部分，一部分为不受旋翼气流影响的自由流区，用下标“wfs”表示，另一部分为受旋翼尾流影响的部分，用下标“wss”表示，下标“w”代表机翼。则机翼气动力为两部分的叠加(机翼气动合力Fw与气动合力矩Mw)，即

(7)

受旋翼尾流影响的机翼面积采用以下经验公式[ 3，9-11]表示，即

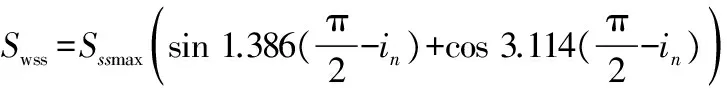
(8)

式中：Sssmax=2ηssRb，R为旋翼半径，b为机翼弦长；umax为旋翼尾迹偏出机翼的最大前进比,是影响系数。机翼自由流区面积Swfs可通过机翼总面积Sw与滑流区面积相减得到。则在机翼上受旋翼尾迹影响后的滑流区速度为

vxRW=[a0+a1i2+a2i2(a3vx+a4i2+a5)]vr·cosi2+vx

(9)

式中：a0～a5为常系数，通过实验方法测得；vr为旋翼产生的平均诱导速度。通过分别计算机翼滑流区与自由流区机翼气动力和力矩叠加可得到机翼整体所产生的气动力和力矩，同时，当发动机短舱角小于60°时，滑流区面积作0处理[12]。

1.3　机身模型

在机身气动力建模过程中，忽略旋翼尾流对机身影响。用气动力和力矩系数的形式来表示，则机身的气动力和力矩为

(10)

式中：Df，Lf，Sf，Mxf，Myf，Mzf分别为机身升力、阻力、侧向力、滚转力矩、俯仰力矩和偏航力矩；Af，lf，qf分别为倾转三旋翼飞行器的机身特征面积、特征长度和机身表面动压；而机身动力和力矩系数CDf，CLf，CSf，CMxf，CMyf，CMzf可通过风洞试验或者流体力学仿真软件计算得到。

1.4　平尾模型

平尾处的旋翼尾流速度参考式(10)，由于倾转三旋翼飞行器结构布局的特殊性，为了方便建模，认为平尾完全处于旋翼发散的尾流之中。则平尾气动中心速度为自身速度和诱导速度的叠加[12-13]，即

(11)

式中：(vxH，vyH，vzH)为平尾中心气动速度；(vxRH，vyRH，vzRH)为旋翼尾流对平尾产生的干扰分量。则可得到平尾的动压

(12)

然后可以得到平尾气动力和力矩为

(13)

式中：cH为平尾弦长;AH为平尾面积。其余参数类似式(9)。

1.5　垂尾模型

倾转三旋翼无人机采用单垂尾模式，与平尾建模分析方法类似，但不需要考虑旋翼尾流的影响。即垂尾中心气动速度与飞行器在机体坐标系下为[vx,vy,vz]，其动压为

(14)

参考式(11)，可得到垂尾的气动力和气动力矩。

2　倾转三旋翼无人机过渡操纵策略与纵向配平

将倾转三旋翼无人机视为刚体，在过渡模式下，做水平定高过渡倾转飞行，则其角加速度、角速度、滚转角和偏航角均为零，则其简化的刚体运动方程为

(15)

式中:∑Fx,∑Fy,∑Fz分别为旋翼、机翼、机身、平尾和垂尾在质心产生的气动力;α为飞行器俯仰角。针对式(15)中的飞行器3个方向气动合力方程，再加上与之相对应的合力矩方程，为倾转三旋翼无人机在过程中配平的主控方程。而针对倾转飞行器同时包含直升机和固定翼飞行器两套操纵方式造成的操纵冗余问题，需要在过渡模式下增加发动机短舱倾转操纵。

本文结合倾转三旋翼无人飞行器的结构构型特殊性，提出了一种基于模糊控制算法的倾转控制方法，将飞行器的倾转过程分为两个阶段，以发动机短舱角为分界点，定义直升机模式向固定翼模式转换过程中前置发动机短舱倾转角in(n=2，3)大于45°为低速倾转阶段，小于45°为高速倾转阶段。过渡模式下各阶段操纵分配如表1所示。

表1　倾转三旋翼无人机过渡模式操纵分配

在倾转三旋翼飞行器过渡模式下，为了保证平稳安全过渡，其参考输入为高度(H)和俯仰角(P)的误差(e)与误差变化率(ec)，通过模糊规则，分别输出相应控制量，经过反模糊化输出发动机短舱期望倾转速度。具体结构见图2。

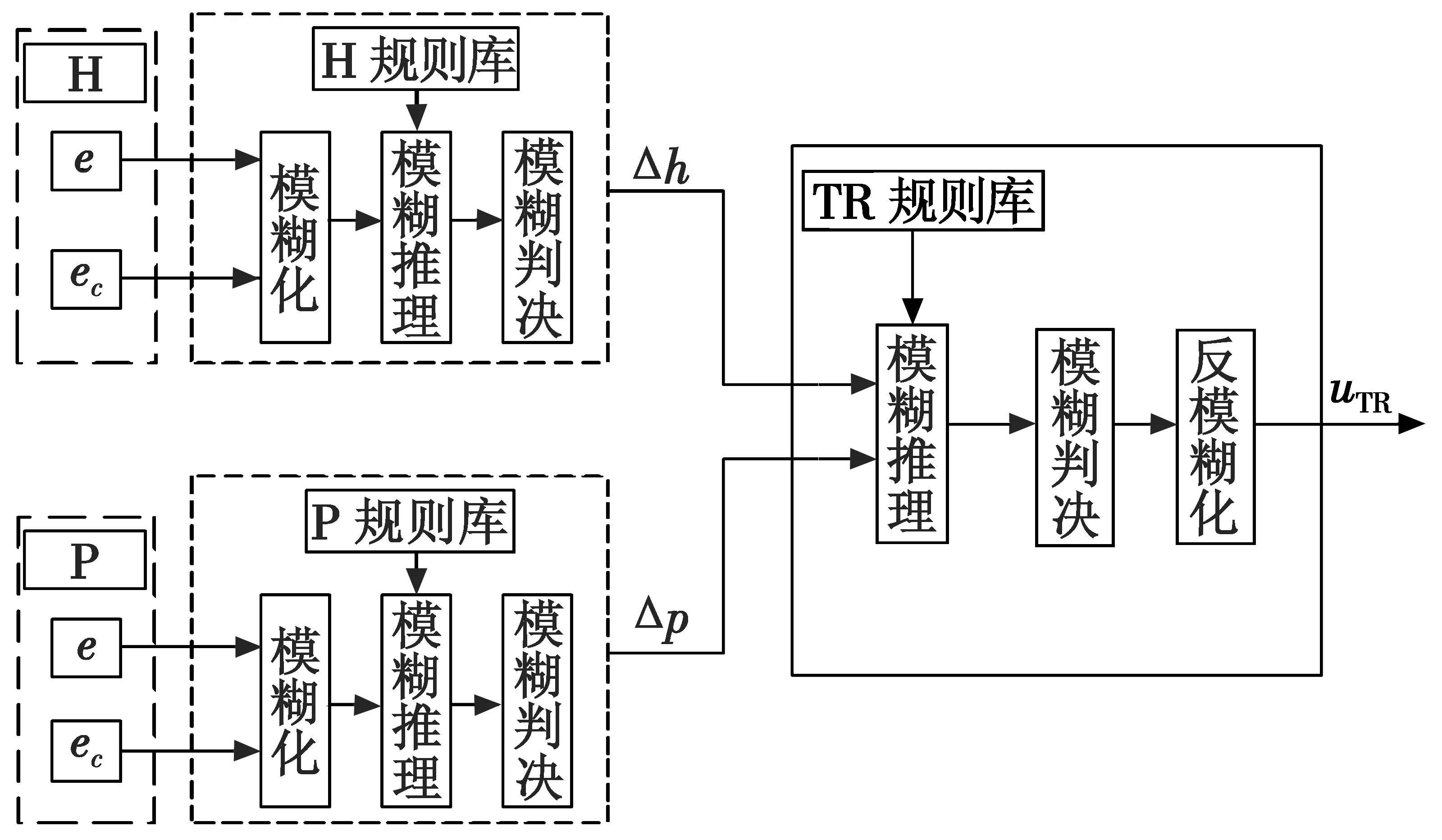
图2　模糊控制结构框图Fig.2　Block diagram of fuzzy control structure

其中，H，P，TR规则库分别为飞行器纵向高度、俯仰角和短舱倾转角速度，模糊控制规则是模糊控制的依据，需要根据经验和实验相结合的方法给出最优规则。表2、表3、表4分别给出了H，P，TR控制规则表。Δh，Δp为经过模糊控制转换后对应的变量结果，ΔTR为发动机短舱控制速度增量。

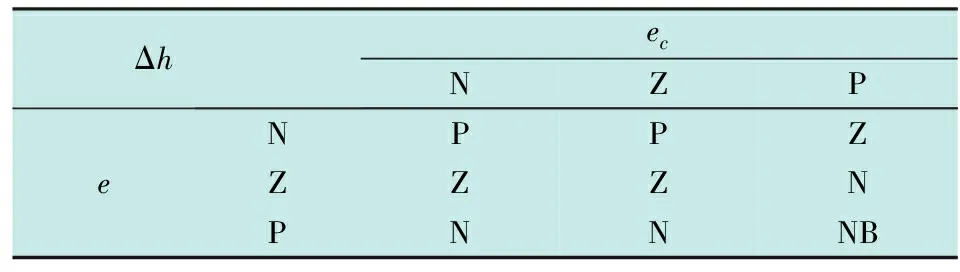
表2　H模糊规则库

表3　P模糊规则库

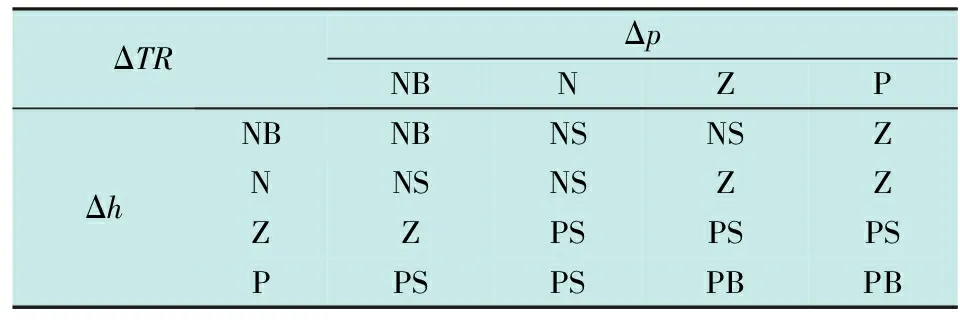
表4　TR模糊规则库

在过渡模式下发动机短舱倾转速度控制原则为当飞行器纵向高度减小且纵向向下速度增大时，为了防止过渡模式掉高过大而坠毁选择减小发动机短舱倾转速度，同时保证飞行器俯仰角在可控范围内，当俯仰角正过大时需要减小短舱倾转速度，负过大时增大倾转速度。飞行器的纵向高度和俯仰角及其与之相对应的变化速度共同决定发动机短舱倾转速度，使倾转三旋翼无人机在过渡模式下能实现平稳高效过渡。

根据实践经验和控制要求分别设置了高度和俯仰角偏差以及偏差变化率模糊集隶属度函数，其中，高度偏差e和偏差变化率ec基本论域分别为(-10,10)，(-4,4)，分别采用3个语言值，俯仰角偏差e和偏差变化率ec基本论域分别为(-20,20)，(-10,10)，也采用3个语言值，发动机短舱角速度控制增量ΔTR基本论域为(-15,15)，采用5个语言值。

3　仿真和实验

为了检验本文所提出的过渡模式控制策略，制作了倾转三旋翼无人机验证样机见图3，具体参数见表5。其中，无人机采用机翼NACA5412翼形，朗宇X2212_980KV无刷直流电机、APC1047螺旋桨。

图3　倾转三旋翼无人机样机Fig.3　Tilt tri-rotor UAV prototype

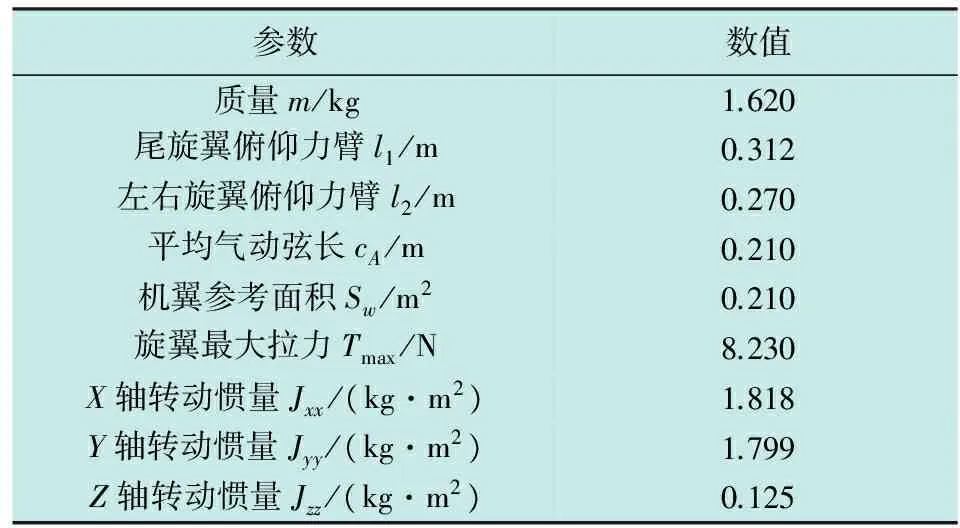
参数数值质量m/kg1．620尾旋翼俯仰力臂l1/m0．312左右旋翼俯仰力臂l2/m0．270平均气动弦长cA/m0．210机翼参考面积Sw/m20．210旋翼最大拉力Tmax/N8．230X轴转动惯量Jxx/(kg·m2)1．818Y轴转动惯量Jyy/(kg·m2)1．799Z轴转动惯量Jzz/(kg·m2)0．125

3.1　理论仿真

利用Matlab仿真软件，在其Simulink环境下搭建模型进行数学仿真，对其发动机短舱倾转速度进行仿真，其仿真结果见图4。通过仿真结果可以看出，当给定短舱倾转角初速度20 (°)/s时，飞行器完成过渡所需时间为3.7 s。短舱倾转速度能够实现稳定加速，达到减小倾转三旋翼无人飞行器过渡模式所需时间，增加飞行可靠性的目的。

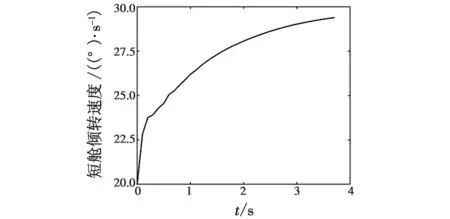
图4　短舱倾转速度仿真曲线Fig.4　Nacelle tilt speed simulation curve

3.2　试验验证

为了验证模糊控制方法对倾转三旋翼无人机过渡模式的控制效果，结合飞行器的实际特点，设计了两组不同控制方法下的倾转过程控制飞行试验。

首先不对发动机短舱倾转速度添加控制，使发动机短舱以20 (°)/s的速度匀速倾转实现飞行器的过渡模式飞行，试验飞行数据见图5。

图5　发动机短舱匀速倾转时飞行高度变化Fig.5　Flight height under engine nacelle constant tilting

然后利用本文所设计的模糊控制方法控制发动机短舱倾转速度使之完成过渡模式飞行，同样给予发动机短舱倾转初速度20 (°)/s，试验飞行数据如图6所示。

图6　采用模糊控制倾转速度后飞行高度变化Fig.6　Flight height under fuzzy control of tilting speed

比较图5和图6可以看出，当不对发动机短舱倾转速度进行控制时，飞行器完成过渡模式飞行纵向掉高30 m，掉高现象严重；而采用模糊方法对发动机短舱倾转速度进行控制，掉高只有7 m，增加了倾转三旋翼无人机倾转过渡模式飞行的安全性，能够对飞行器过渡过程纵向飞行高度有效控制。

4　结论

本文针对倾转三旋翼无人机过渡模式下的操纵策略进行了研究，建立了飞行器过渡模式数学模型，将过渡模式分为低速阶段和高速阶段，设计了一种以过渡过程中纵向高度变化和俯仰角变化为参考输入，通过模糊规则控制发动机短舱倾转角速度，使无人机过渡模式平稳高效转换。最后飞行试验表明：采用基于模糊控制策略的过渡模式操纵策略能够有效抑制倾转三旋翼无人机过渡过程中的掉高现象，提高无人机飞行安全性，达到过渡模式平稳高效飞行的目的。

[1]PAPACHRISTOS C,TZES A．Modeling and control simulation of an unmanned tilt tri-rotor aerial vehicle[C]//IEEE International Conference on Industrial Technology, 2012:840-845.

[2]OZDEMIR U,AKTAS Y O,VURUSKAN A,et al.Design of a commercial hybrid VTOL UAV system[J].Journal of Intelligent & Robotic Systems,2014(1/2):371-393.

[3]NOTARSTEFANO G,HAUSER J.Modeling and dynamic exploration of a tilt-rotor VTOL aircraft[J].IFAC Proceedings Volumes,2010,43(14):119-124.

[4]陈坤，史志伟，孙加亮.倾转三旋翼飞行器地面效应风洞试验[J].航空学报，2015,36(9)：2884-2891.

[5]万华芳．倾转旋翼飞行器过渡段仿真研究[D]．南京：南京航空航天大学，2011．

[6]曹芸芸,陈仁良.倾转旋翼飞行器的操纵策略和配平方法[J]．南京航空航天大学学报，2009，41(1)：6-10．

[7]高正，陈仁良．直升机飞行动力学[M].北京：科学出版社，2003:24- 42．

[8]王适存.直升机空气动力学[M].南京：航空专业教材编审组，1985:68-72．

[9]杨阳,崔金峰，余毅．三旋翼飞行器动力学分析及建模[J]．光学精密工程，2013，21(7)：1873-1880．

[10]夏青元，徐锦法，金开保．倾转旋翼飞行器的建模和操纵分配策略[J]．航空动力学报，2013，28(9)：2016-2028．

[11]陈永．倾转旋翼机过渡段纵向姿态控制技术研究[D].南京：南京航空航天大学，2011.

[12]夏青元，徐锦法，金开保.倾转旋翼飞行器的建模和操纵分配策略[J].航空动力学报，2013，28(9)：2016-2028.

[13]陈永，龚华军，王彪.倾转旋翼机过渡纵向姿态控制技术研究[J].飞行力学，2011，29(1)：30-33.