双层平尾对旋翼/平尾干扰的抑制机理研究

孙会迅，孙朋朋，林永峰，曾 伟

(中国直升机设计研究所 直升机旋翼动力学重点实验室，江西 景德镇 333001)

0 引言

平尾起到改善直升机纵向操作性及稳定性的作用。小速度前飞时受旋翼尾迹作用，平尾的气动力突然变化，将引起直升机俯仰力矩的突变，对直升机的操作带来不利影响[1]。由于现代直升机桨盘载荷增加和机身结构愈发紧凑，旋翼与平尾干扰问题更加突出。常规直升机平尾为单层平尾，设计时考虑平尾的布置位置等参数来减弱旋翼/平尾干扰[2]。然而，最先进的H160 直升机创新地采用双层平尾设计，给未来直升机平尾设计带来新的思路。因此，针对双层平尾的旋翼/平尾气动干扰问题的研究具有重要意义。

对于旋翼/平尾的气动干扰问题，国外研究者通过试验和数值模拟方法开展了大量研究。1998年,Erwin等[3]采用风洞试验测量了旋翼和T型平尾干扰流场，研究了T型平尾的载荷随前进比的变化规律，对不同前进比下的旋翼尾迹特点与平尾载荷变化规律进行了详细分析。2002年，Susan等[4]采用激光测速系统测量了平尾前方流场速度，结果表明：由于旋翼尾迹影响，平尾来流迎角非定常变化，变化范围达30°。在前进比0.1时，旋翼尾迹对该T型平尾影响最大。在GOAHEAD项目支持下，2012年，意大利宇航局建立了GOAHEAD 直升机模型，Fabrizio[5]试验研究其三维速度场和流动干扰，分析了平尾引起的抬头现象,认为桨尖涡冲击到平尾，产生抬头现象。M. Biava等[6]采用ROSITA求解器模拟了整个GOAHEAD 直升机模型流场，与试验结果进行了详细对比，分析了平尾流场及其平均攻角，认为旋翼尾迹通过增加平尾平均攻角来影响平尾性能。2019年，Markus等[7]采用CFD方法(Computational Fluid Dynamics)和结合自由尾迹模型的非定常面元法模拟了旋翼/平尾干扰问题，模拟结果与全尺寸飞行试验数据符合较好，同时分析了低平尾和T型平尾气动干扰规律。国外研究者对单层平尾构型的旋翼/平尾的干扰问题展开了大量研究，目前没有对双层平尾构型的旋翼/平尾气动干扰问题的相关研究。

在国内，中国空气动力研究与发展中心的孙正荣以及清华大学的谭剑锋等对单层平尾在不同前进比状态的旋翼/平尾气动干扰问题进行了试验和计算研究[8-9]；王鑫磊等[10]采用数值计算方法研究了前缘缝翼构型平尾气动特性。然而，针对双层平尾的旋翼/平尾气动干扰研究还没开展过。

鉴于此，本文采用数值计算的方法研究了双层平尾对旋翼/平尾干扰的抑制机理。流场计算基于动量源模型的CFD方法，采用典型气动干扰试验数据对气动干扰计算精度进行了验证。参考H160直升机，建立单层和双层平尾的旋翼/平尾计算模型，对多个前进比下的旋翼/平尾气动干扰流场进行了计算，分析了单层和双层平尾的干扰载荷变化规律和流场特征，研究了双层平尾对旋翼/平尾干扰的抑制机理，为未来直升机平尾设计做有益探索。

1 计算方法及验证

1.1 基于动量源模型的数值计算方法

采用包含动量源项的CFD方法来计算旋翼/平尾干扰流场，由桨盘模型代替旋翼，即通过作用盘理论将旋转的桨叶等效为作用盘，作用盘对流场的力来模拟旋翼桨叶对流场的影响。用时间平均的动量源项代替旋翼对流场的效用，再将动量源项添加到控制方程。N-S方程计算时采用有限体积法对空间进行离散；时间离散采用五步Runge-Kutta格式；梯度方法选择格林高斯方法；湍流模型选择SA模型；壁面边界条件为无滑移壁面；远场边界条件为压力远场。基于动量源模型的CFD方法计算流程如图1所示。

图1 基于动量源模型的CFD方法计算流程图

1.2 计算方法验证

为证明本文使用的计算方法准确可靠，采用经典的Robin模型验证计算方法。Robin模型包含超椭圆机身和四片桨叶，旋翼参数如表1所示[11]。

表1 Robin旋翼参数

对计算模型划分网格，网格类型为四面体和棱柱体混合网格，网格总数约为435万。图2为计算网格图。

图2 Robin模型计算网格

计算悬停(μ=0.01)和前飞(μ=0.15)两个状态，与公布的试验数据进行对比。配平方法采用牛顿迭代法，配平目标为计算拉力系数与试验拉力系数一致。

图3为机身上两个流向位置的时均压力分布，计算结果与试验数据拟合较好，但在x/l等于1.17位置处，有较大偏差。这是由于数值计算时没有考虑试验中的支架影响导致的。对比结果表明计算方法能够准确预测气动干扰问题。

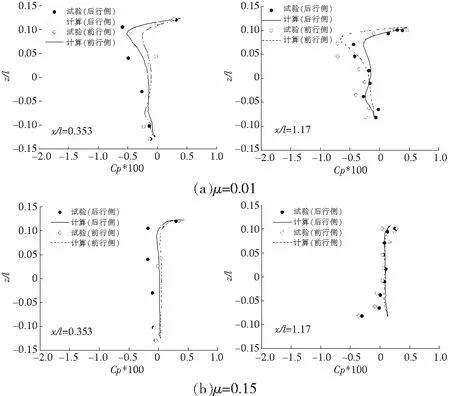
图3 机身上两个流向位置的时均压力分布

2 双层平尾的旋翼/平尾干扰研究

2.1 计算模型

旋翼/平尾气动干扰引起严重的直升机稳定性和操纵性问题。旋翼尾流位置随飞行状态改变而改变。尾流与平尾干扰，使得平尾处产生很大的力和力矩。本节采用CFD方法获得了旋翼/平尾干扰计算结果，分析了双层平尾与单层平尾的气动干扰特征。

参考H160平尾结构和相对位置，建立双层平尾与旋翼干扰计算模型，旋翼采用Robin模型中旋翼。本论文目前只考虑旋翼和平尾的气动干扰问题，因此计算模型中只包含旋翼和平尾。双层平尾结构如图4所示，其具体参数如表2所示。

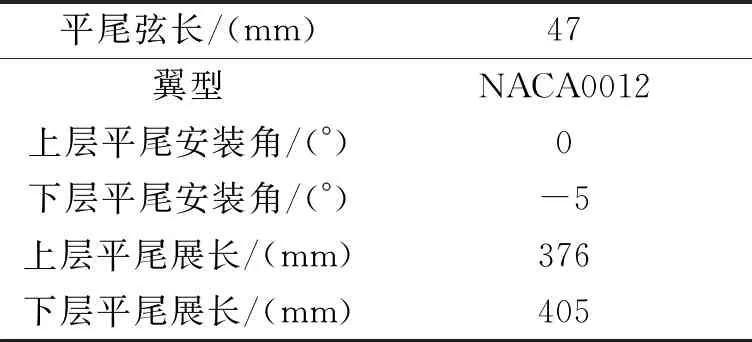
表2 双层平尾参数

图4 双层平尾几何模型

建立单层平尾为对比模型。平尾主要作用是改善直升机迎角静稳定性，因此，要保证单层平尾与双层平尾的的俯仰力矩系数斜率和截距基本相同。如图5所示，单层和双层平尾的俯仰力矩系数的斜率和截距基本相等。单层平尾具体参数如表3所示。

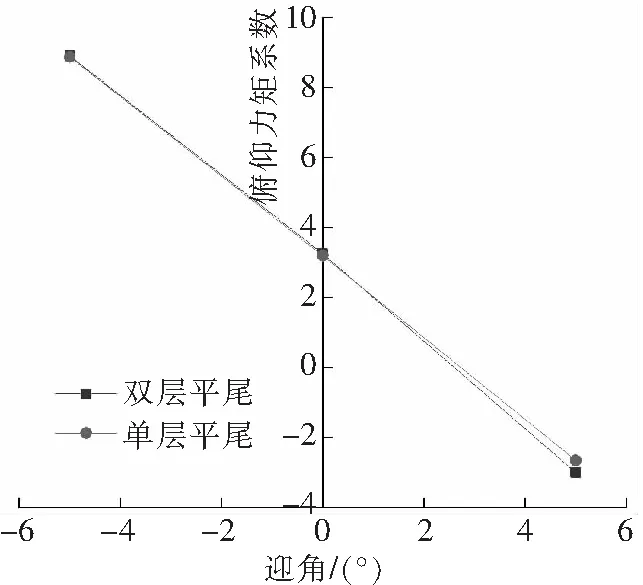
图5 平尾俯仰力矩系数与迎角关系曲线

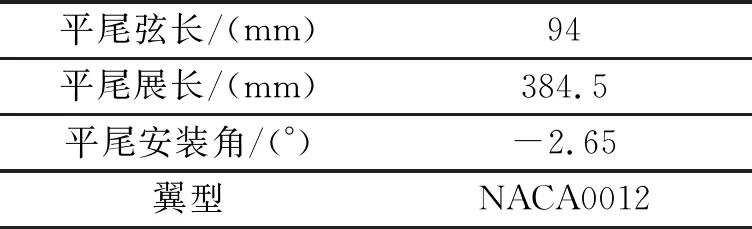
表3 单层平尾参数

对几何模型划分四面体/棱柱混合网格，对平尾周围进行局部加密。单双层平尾计算模型的网格设置基本一致，双层平尾计算模型网格数约为713万，单层平尾计算模型网格数约为347万。网格如图6所示。

图6 计算模型网格截面图及局部放大图

在相同旋翼拉力系数(CT=0.0064)下，计算不同前进比下的旋翼/平尾干扰流场。配平方法为牛顿迭代法，配平变量为总距、横向和纵向周期变距，轴倾角按照Robin试验结果给定。

2.2 旋翼/平尾气动干扰结果分析

本节对计算结果进行分析，分析双层平尾与单层平尾的气动干扰特征。首先探讨平尾的干扰载荷随前进比的变化规律；之后通过流场分析和压力分布对比，探讨双层平尾对旋翼/平尾干扰的抑制机理。

2.2.1 干扰载荷

图7为平尾干扰载荷随前进比变化的关系曲线，干扰载荷为扣除无干扰情况的平尾载荷(垂向力)。在前进比0.01～0.05之间，随着前进比的增加，旋翼尾迹向尾部移动并撞击平尾，两种构型的平尾干扰载荷显著增加。在前进比0.05状态，干扰载荷最大，但双层平尾的干扰载荷约为单层平尾干扰载荷的57%，证明双层平尾构型可以在小前进比状态抑制旋翼/平尾干扰，能够改善过渡飞行状态下机体姿态剧烈变化。在前进比0.05～0.15之间，旋翼尾迹继续向后移动，两种构型平尾的干扰载荷减小。在前进比0.15～0.23时，随前进比增加，干扰载荷继续增加。在前进比0.1～0.23之间，单层平尾和双层平尾的干扰载荷相差不大。

图7 平尾干扰载荷与前进比关系曲线

图8为双层平尾干扰载荷随前进比变化的关系曲线。上层平尾的干扰载荷随前进比变化规律与单层平尾的干扰载荷变化规律基本一致，但是上层平尾的干扰载荷数值较低：强干扰状态(μ=0.05)下，上层平尾干扰载荷约为单层平尾干扰载荷的56%。这是由于双层平尾的上下双层设计降低了单层平尾弦长，从而降低了旋翼尾迹撞击在平尾上而产生的干扰载荷。

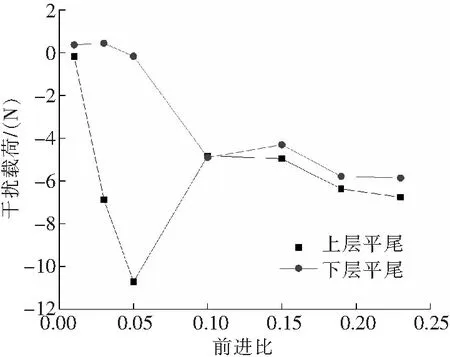
图8 双层平尾干扰载荷与前进比关系曲线

对于下层平尾，在前进比0.01～0.05之间，下层平尾干扰载荷很小且基本不变，表明下层平尾受旋翼尾迹干扰较小；在前进比0.1～0.23之间，下层平尾干扰载荷变化规律与上层平尾干扰载荷变化规律基本一致。

2.2.2 旋翼/平尾干扰流场

以单层平尾流场为例分析旋翼/平尾的干扰过程。如图9所示，近悬停状态(μ=0.01)，在旋翼下方尾流向内收缩，平尾没有受到旋翼尾流干扰；前进比为0.05时，旋翼尾流向后方偏斜，尾流撞击平尾，平尾沉浸在旋翼尾流中，此时旋翼/平尾干扰严重，平尾干扰载荷很大；前进比为0.15时，旋翼尾流继续向后方偏斜，尾流不再直接撞击平尾，对应平尾载荷显著下降；前进比为0.23时，尾流继续向后方偏斜，此时平尾干扰载荷仍比较大，有文献[12-13]指出这是与涡线的扭曲和拉伸作用有关的另一种形式的干扰，此时干扰峰值比尾流撞击平尾时的干扰峰值小。

图9 不同前进比下，旋翼诱导速度分布及流线图

2.2.3 双层平尾抑制干扰机理分析

由图7平尾干扰载荷与前进比关系曲线可知，在前进比0.05状态下，旋翼/平尾干扰效应显著，双层平尾对旋翼/平尾干扰有明显的抑制作用。本节对前进比0.05状态下的流场展开分析，对双层平尾干扰抑制机理进行讨论。

如图10(a)旋翼干扰下的单层平尾表面压力云图所示，在强干扰状态下(μ=0.05)，旋翼尾流冲击单层平尾，气流冲击使得单层平尾上翼面压力增大。如图10(b)旋翼干扰下的双层平尾表面压力云图所示，上层平尾的压力分布与单层平尾压力分布相似，也受到旋翼尾流的冲击，但双层平尾的上下双层设计降低了上层平尾的面积，从而降低了旋翼尾迹撞击在平尾上而产生的干扰载荷。除端部外，下层平尾压力较小，与无旋翼干扰状态下的下层平尾压力分布(如图10(c)所示 )基本相同。这是由于上层平尾对下层平尾的遮挡作用，减弱了下层平尾受到的旋翼尾迹干扰。

图10 前进比为0.05时，平尾表面压力

定义压力系数为：

Cp=(P-P∞)/(0.5×ρV∞2)

(1)

其中，P∞为远场压力，V∞为自由来流速度。

由图11Y=0(平尾的对称截面)剖面的压力系数分布发现，单层平尾和双层平尾的上层平尾的剖面压力分布基本一致。压力分布特征表明，受旋翼尾迹影响，平尾处于大负迎角环境。由于旋翼尾迹的撞击，单层平尾和双平尾的上层平尾的上表面压力系数为正。而下层平尾的翼型剖面压力系数全为负，下层平尾载荷较小，表明下层平尾受旋翼尾迹影响较小。

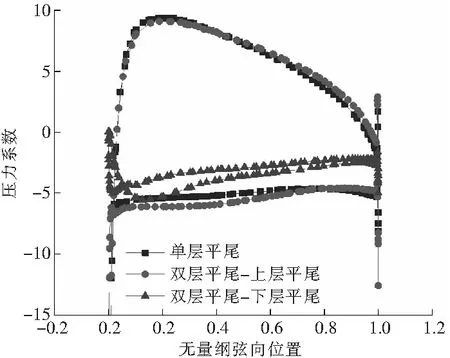
图11 前进比0.05时，平尾Y=0剖面压力系数分布

下层平尾展向剖面的压力分布如图12所示，不同剖面处压力分布特点不同，大部分剖面处流动为逆压流动。由图13双层平尾Y=0截面的压力云图和流线图可知，旋翼尾流撞击上层平尾，气流在上层平尾上表面滞止，压力增大。

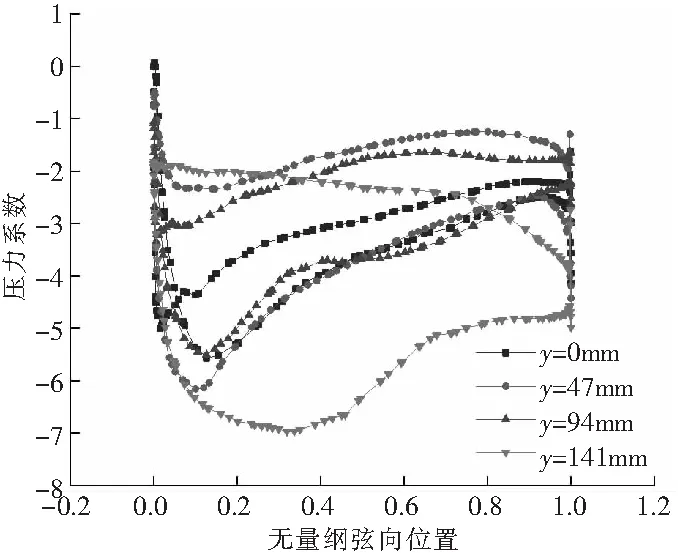
图12 前进比0.05时，下层平尾展向剖面的压力系数分布

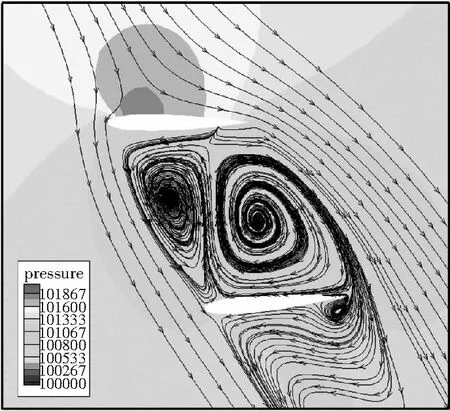
图13 前进比0.05时，Y=0截面的压力云图和流线图

上层平尾阻挡旋翼尾流，从而避免了下层平尾受到旋翼尾流冲击，因此上层平尾的遮挡作用抑制了旋翼尾流对下层平尾的干扰。

3 结论

本文建立了单层和双层平尾的旋翼/平尾气动干扰计算模型，分析了旋翼干扰下的平尾气动特性和流场，研究了双层平尾抑制旋翼/平尾干扰的机理，主要得到以下结论：

1)双层平尾对旋翼/平尾干扰有抑制作用，能够改善过渡飞行状态下机体姿态剧烈变化。小前进比(μ=0.05)状态下，相比单层平尾，双层平尾的干扰载荷下降约43%。

2)上层平尾的干扰载荷变化规律与单层平尾的干扰载荷变化规律基本一致，表明上层平尾干扰载荷主要是受旋翼尾迹影响。强干扰状态(μ=0.05)上层平尾干扰载荷约为单层平尾的干扰载荷的56%，这是由于双层平尾的上下双层设计降低了单层平尾弦长，从而降低了由于旋翼尾迹撞击而产生的干扰载荷。

3)小前进比状态，下层平尾处在上层平尾的尾流区中，其周围流动十分复杂；上层平尾的遮挡作用减弱了旋翼尾迹对下层平尾的冲击干扰，抑制了旋翼/平尾干扰。