扇形航路雷达探测式反潜巡逻机绩效评估方法*
朱丰,胡晓峰,郭圣明,姚庆锴,任远,杨璐
(1.中国人民解放军国防大学,北京 100091;2.中国人民解放军军事科学院,北京 100091;3.中国人民解放军95801部队,北京 100843;4.海军研究院 复杂舰船系统仿真重点实验室,北京 100161;5.空军工程大学防空 反导学院,陕西 西安 710051)
0 引言
在信息化联合作战中,完成预警探测任务的预警探测体系是作战力量中不可或缺的重要组成部分之一。反潜巡逻机(包括旋转翼和固定翼的反潜巡逻机)作为预警探测体系中的一项关键组成部分,对于完成预警探测任务起到了重要作用。特别是固定翼反潜巡逻机,由于其具有速度快、机动性强、可携带多种探测设备、搜潜效率高、不易被潜艇攻击等特点,因此,对于探索、发现并持续跟踪敌方水下潜艇起到了核心作用[1-5],从而也被各国军队特别是海军部队所重视。目前,反潜巡逻机已成为各国海军编队反潜作战的重要力量,也得到了各国军队的重点发展。现在正在服役的反潜巡逻机主要有,美国的“猎户座”P-3C与“北欧海盗”、英国的“猎迷”、俄罗斯的伊尔-38等,后续还要大力突破更先进的反潜巡逻机。
由此观之,在信息化的联合作战战场上,为有效夺取制海权,加强反潜巡逻机建设是毋容置疑的。那么,如何更有效地开展反潜巡逻机建设,其中一个关键环节就是要对其绩效进行合理的评估。
目前,常用的评估方法主要包括:ADC(availability,dependability,capacity)法、层次分析法、指数法、解析法、作战仿真模拟法和专家评估法等[6]。这些方法各具特点,也各有其适用范围。ADC法需要拥有明确的系统构成要素和相应的性能指标,层次分析法基本离不开分析人员的主观评估,对于分析人员评估水平依赖性较大,且其定性分析的成分较大,解析法难以处理相对独立的效能因素,且通常计算量较大,效率不高。专家调查评估法容易受传统思维的影响。综合而言,这些方面要么计算复杂,不利于简单便捷,要么主要依赖于人的因素,主观性影响过重。因此,如何寻求相对便捷的、简单的,且尽可能客观的评估方法,是有待研究的重要问题。
本文就此展开了一定的研究,针对扇形航路形式下,以机载雷达探测方式来实施搜索探测的反潜巡逻机绩效评估问题进行了有益探索,结合反潜巡逻机的工作特点,通过建立基于搜索区域面积和持续巡逻时间的数学模型[7],提出了一种面向反潜巡逻机绩效评估的新方法。该方法通过对搜索区域面积和持续巡逻时间进行概略评估,从而达到简单、便捷的效果。同时,该方法是基于计算解析的方法,因此,可客观、合理、高效地实现反潜巡逻机绩效评估。最后,本文给出了一个实验案例来验证本文所提方法的有效性。
1 反潜巡逻机的工作特点
反潜巡逻机包括岸基和舰基2种,它们在执行巡逻任务时,其机载雷达的主要功能都是对在潜望镜、通气管状态的潜艇进行搜索、识别和跟踪。这种机载雷达对潜艇的搜索主要是对大面积海域进行巡逻搜索,因为无论是核潜艇还是常规潜艇都要定期浮出水面,例如①常规潜艇使用柴油机航行时,必须要伸出通气管;②潜艇进行天体定位时,必须浮出水面;③潜艇与基地进行无线电通信时,需要伸出天线;④受水下环境影响,活动深度受到限制时,不得不上浮或呈半潜状态;⑤潜艇对舰船目标进行瞄准攻击时,必须伸出雷达天线或呈潜望镜。可以说,潜艇的这种活动规律为雷达探测创造了条件[8-12]。
通常,岸基反潜巡逻机、舰基反潜巡逻机分别在陆基机场中和在舰船上会根据预先指定的巡逻任务配好装备和补给。当领受到开始执行巡逻任务时,岸基反潜巡逻机从陆地上起飞,舰基反潜巡逻机从舰船上起飞,经过一段时间的航行到达指定的巡逻区域,然后在巡逻区域内执行巡逻搜索任务。当指定的巡逻时间期限已满,或根据上级的返航指挥命令,即按指定航线返航。这个过程如图1所示。
反潜巡逻机在巡逻区域中巡逻时的工作方式主要从2方面来探讨。
一是其航路形式,通常有:平行航线式、扩展式和扇形形式等。其中,扇形航路形式是反潜巡逻机特别常见的一种典型的工作方式,由此,本文就扇形形式进行具体探讨分析,航路示意图如图2所示。
假设P1P9P10为待搜索等边三角形区域,飞机从A点起飞,在B点进入准备搜索阶段,并转弯进入到C点,由C点直飞到D点(C,D点间距离很近可忽略不计),再由D点转弯180°到P1点。从P1开始进入检查搜潜阶段,P1到P2为直飞过程,P2到P3为顺时针转弯过程,P3到P4为直飞过程,P4到P5为逆时针转弯过程,P5到P6为直飞过程,P6到P7为顺时针转弯过程,然后依次往后搜索,直至搜索完毕。
反潜巡逻机一般在指定巡逻线(或巡逻区域)上搜索。巡逻线既可以是固定不动的,也可以是相对固定的。
二是其探测搜索方式,可利用目视观察、雷达探测[13],也可使用声呐浮标、吊放声呐、磁异探测仪以及红外探测仪、废气探测仪、电场分析仪、激光探测仪等来搜索潜艇[14]。其中,雷达探测是一种非常重要的方式,因此,本文就雷达探测方式展开研究[15]。
通常,装备在反潜巡逻机上用来搜索探测目标的雷达,即为机载雷达,通过向海面的俯视(需要一定的视轴俯角)来完成对潜艇的搜索探测,机载雷达探测的几何模型如图3所示。
当反潜巡逻机飞行高度h、雷达视轴俯角θ一定时,在确定的垂直波束角θr下,感知环宽度ρ是反潜巡逻机空间状态的函数,如式(1)所示,其几何关系如图4所示意。
ρ=f(h,θ,θr),
(1)
式中:雷达垂直波束角θr在反潜巡逻机飞行高度h和雷达视轴俯角θ一定时,由l01和l02决定;f(·)为非线性函数。
2 反潜巡逻机绩效评估方法
依据反潜巡逻机的工作原理,假设每架反潜巡逻机的最大航程均为Lkm,则该航程可拆分为
L=L0+LW+LZ+LB,
(2)
式中:L0为反潜巡逻机从起飞处到搜索区域之间经过的往返路程,该路程过长,可能会影响反潜巡逻机侦察搜索效能的发挥程度,因此,应根据实际作战需要酌情考虑;LW为M条弯道路径的总长度(M≥2);LZ为N条直线路径的总长度;LB为从搜索结束点返回到搜索起始点的路程,它们的单位均为km,分别满足
LW=πMR,
(3)
(4)
(5)
式中:M≥N,一般情况下,M=N+1;R为转弯半径,

图1 反潜巡逻机执行巡逻任务示意图Fig.1 Sketch of performance of antisubmarine patrol aircraft executing patrol mission
单位为km,其满足如下公式
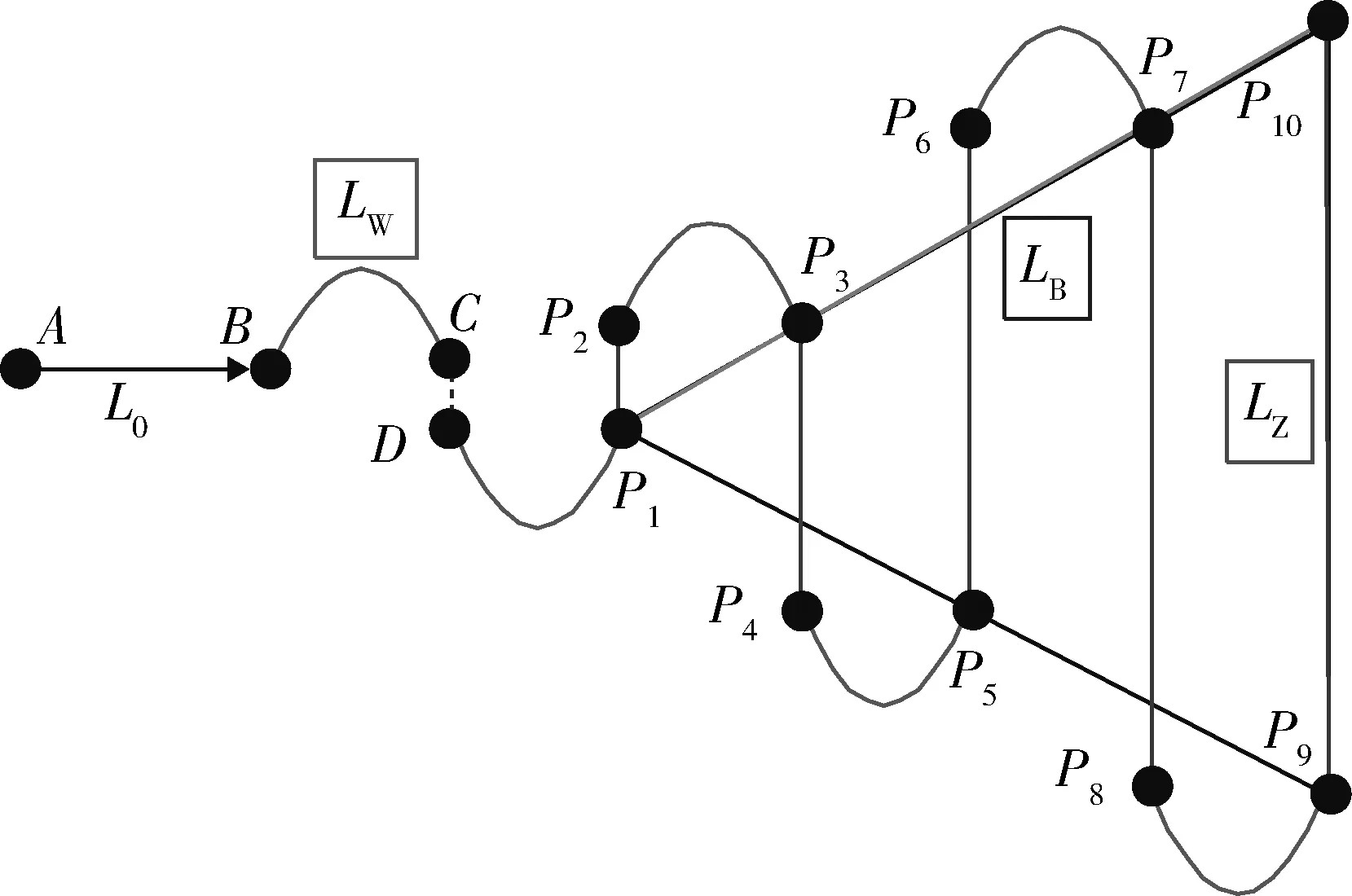
图2 载有探测雷达的反潜巡逻机在巡逻区域内的扇形航路示意图Fig.2 Sketch of sector airway of antisubmarine patrol aircraft with detected radar in patrol area
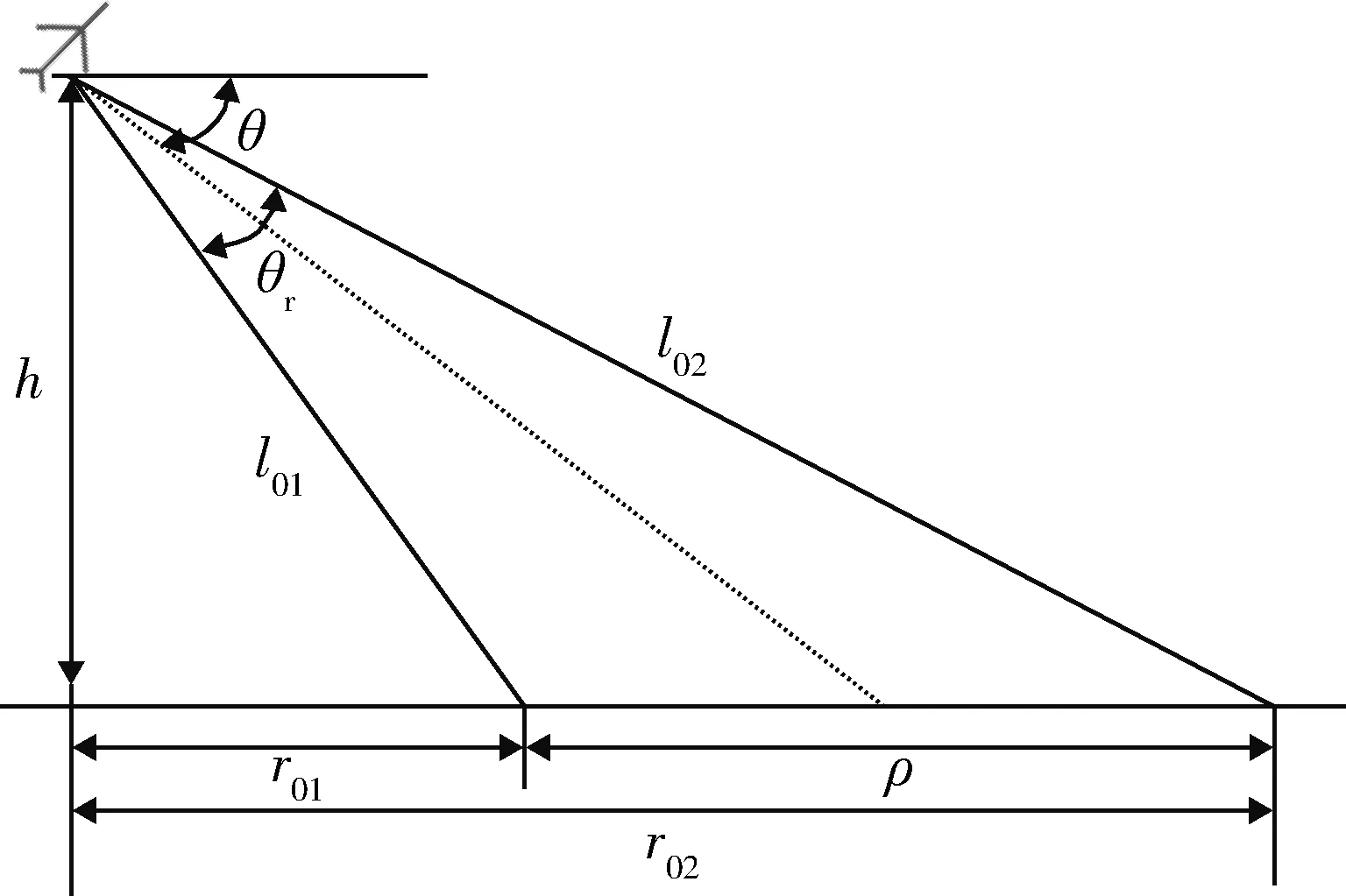
图3 反潜巡逻机机载雷达感知环示意图Fig.3 Sketch of radar awareness ring of antisubmarine patrol aircraft

图4 反潜巡逻机机载雷达感知环俯视示意图Fig.4 Sketch of overlooking radar awareness ring of antisubmarine patrol aircraft

(6)
式中:g为重力加速度,g=9.8 m/s2=127 008 km/h2;v为反潜巡逻机的航行速度,单位为km/h;ω为反潜巡逻机转弯角速度,通常是个定值。
由此,在反潜巡逻机执行侦察巡逻任务时往返飞行的到达路径长度L0和转弯半径R(即与航行速度和转弯角速度有关)一定的条件下,可以得到关于反潜巡逻机最大航程L与弯道路径条数M或与直线路径条数N的函数关系。
进一步可以推导出,考虑到反潜巡逻机机载雷达感知环还有一定的面积,因此,每架反潜巡逻机沿航路飞行时的搜索区域面积Ss(单位:km2),可用如下公式近似表达,并如图5所示(图中若干绿色曲线表示不同时刻下反潜巡逻机机载雷达的感知外界,黑色虚线围成的区域即为反潜巡逻机沿航路飞行时的整个搜索区域)。通常,反潜巡逻机弯道飞行的转弯半径R小于等于反潜巡逻机在水平面上的投影到机载雷达感知环最外边界的距离r02,本文就此情况展开论述分析。

图5 反潜巡逻机沿航路飞行时近似的搜索区域示意图Fig.5 Sketch of approximate search area ofantisubmarine patrol aircraft flyingalone the airway
Ss=S0+S1,
(7)
式中:S0(单位:km2)为反潜巡逻机飞行航迹所围成的区域面积,这些面积都是反潜巡逻机的搜索面积,其满足
(8)
而S1(单位:km2)则为反潜巡逻机在飞行航迹所围成的区域面积之外,由机载雷达感知所扩充的近似搜索面积,其计算如下:
(9)
因此,可获得近似的搜索区域面积为
(10)
通过如上几个公式,可以建立起每架反潜巡逻机执行侦察巡逻任务时其所顾及到的搜索区域面积Ss与最大航程L之间的相互关系。
假设反潜巡逻机执行侦察巡逻任务计划要完成搜索的总区域面积为Skm2,则从搜索面积角度来看,共需要反潜巡逻机的架数JS为

(11)
式中:「·⎤表示向正无穷大取整数;α为搜索面积重叠因子,可取α∈[0,1],通常α>0.5。
这是因为任意2架不同的反潜巡逻机在执行侦察巡逻任务时,其各自负责的搜索区域之间要有一定的重叠,一方面,搜索区域形状为扇形,难以将所计划的全部搜索区域依扇形进行严格的分割;另一方面,在搜索时,有一定的重叠区域也可进一步降低搜索漏警率,更加确保搜索质量;向正无穷大取整数的目的是执行任务时对反潜巡逻机数量的要求秉着“宁多勿少”的原则,特别是计算出的结果为小数时,要取更大一级的整数,确保执行侦察巡逻任务的反潜巡逻机数量足够。
再假设侦察巡逻任务要反潜巡逻机每日的持续巡逻时间为T,反潜巡逻机每日的起飞批次为n次/日,则从持续巡逻时间角度来看,共需要反潜巡逻机的架数JT为

(12)
式中:「·⎤表示向正无穷大取整数;β为巡逻时间重叠因子,与α类似,可取β∈[0,1],通常β>0.5。分析其中的缘由,与前文分析从搜索面积角度来看共需要反潜巡逻机架数JS的情况一致;T0为反潜巡逻机执行侦察巡逻任务时的持续巡逻时间,单位为h,可通过如下公式计算得到
(13)
综合上述2个分析角度,可以得出为完成侦察巡逻任务,共需反潜巡逻机的总架数J为
J=JSJT.
(14)
需要说明的是:文中的许多等号可能并非是严格的等号,严格意义上讲,应该为约等号,但由于本文提出的基于等效面积的反潜巡逻机绩效评估方法是个概略计算的方法,并不追求过多的精确性,因此,文中将其进行简化,统一使用等号处理以便于表达和计算。
依据本文所述内容,本文提出的反潜巡逻机绩效评估方法流程图如图6所示。
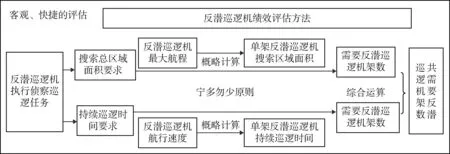
图6 反潜巡逻机绩效评估方法流程图Fig.6 Flow chart of performance assessment method of antisubmarine patrol aircraft
3 案例分析
依据文献[6-9,15]中的仿真实验参数,假设反潜巡逻机的最大航程L为1 000 km,航行速度v为320 km/h,飞行高度h为300 m,视轴俯角为20°,l01=0.560 0 km,l02=1.612 0 km,可知其在水平面上的投影到机载雷达感知环最外边界的距离r02=1.588 0 km,假设反潜巡逻机在弯道飞行时的转弯角速度ω为30°,则根据本文所述公式可以计算得到其转弯半径为R=1.396 5 km。
同时,按照本文方法,还可获得每架反潜巡逻机所顾及到的搜索区域面积Ss、持续巡逻时间T0分别与最大航程L之间的相互关系图如图7所示,其中假设往返路程L0为100 km,此时假设反潜巡逻机为岸基的。从图中可以看出,本文实验案例中单架反潜巡逻机所顾及到的搜索区域面积Ss为2 198.45 km2,持续巡逻时间T0为2.812 5 h。
假设反潜巡逻机计划搜索区域的总面积S为15 000 km2,每日24 h全天时巡逻,即T=24,每日的起飞批次n为2次/日,取α=0.8,β=0.8,则计算出JS=9,JT=6,由此得到共需反潜巡逻机的总架数J为54架,如图8a)所示意。
进一步地,将岸基反潜巡逻机改为舰基的,往返路程L0可记为0 km,由此可获得每架反潜巡逻机所顾及到的搜索区域面积Ss、持续巡逻时间T0分别与最大航程L之间的相互关系图如图9所示。从图中可以看出,本文实验案例中单架反潜巡逻机所顾及到的搜索区域面积S0为2 458.79 km2、持续巡逻时间T0为3.125 0 h。则可进一步计算出JS=8,JT=5,由此得到共需反潜巡逻机的总架数J为40架,如图8b)所示意,其他实验参数均与岸基情况时的参数一致。
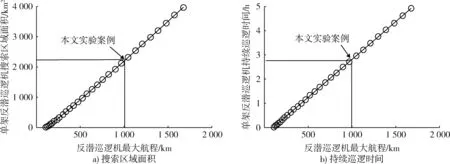
图7 岸基单架反潜巡逻机最大航程与相关性能间的相互关系曲线图Fig.7 Curve of correlation between the maximum voyage and relevant attributions of single land based antisubmarine patrol aircraft

图8 反潜巡逻机绩效评估结果示意图Fig.8 Sketch of performance assessment results of antisubmarine patrol aircraft

图9 舰基单架反潜巡逻机最大航程与相关性能间的相互关系曲线图Fig.9 Curve of correlation between the maximum voyage and relevant attributions of single ship based antisubmarine patrol aircraft
从岸基反潜巡逻机与舰基反潜巡逻机的绩效评估结果来看,舰基的情况比岸基在其需要54架的条件下要少需要14架反潜巡逻机,少需要25.93%,这主要是由于舰基的情况是反潜巡逻机在海上直接起飞出发,从而减少了往返的路程,这是符合实际情况的。因此,可作为结果依据供军事指挥和研究人员参考。同时,这个实验案例也验证了本文所提方法的有效性。
4 结束语
本文着眼于当今重要的军事需求,针对反潜巡逻机绩效评估问题展开了一定的研究工作。在论述分析了反潜巡逻机(包括岸基和舰基2种)工作特点的基础上,结合相关内容,建立了合理的数学模型,提出了一种面向扇形航路形式和机载雷达探测方式的反潜巡逻机绩效评估新方法。该方法通过对搜索区域面积和持续巡逻时间进行概略评估,从而达到了简单、便捷的效果,可客观、合理、高效地实现一定的反潜巡逻机绩效评估。实验案例不仅验证了本文所提方法的有效性,而且表明在本文实验条件下,舰基反潜巡逻机的需要情况比岸基的(需要54架)要少14架,少需要25.93%,这个结果可作为结果依据供军事指挥和研究人员参考。本文工作可为研究如何评估作战体系、系统等的作战效能问题提供理论和技术支持,也可为其他评估问题的研究突破提供新的思路和方法。所开展的相关研究工作仍在不断的深入和逐步拓展。

