曲线拟合法在黄土路基沉降预测中的应用

李志雷 王 伟 蔡 旺

(武汉理工大学交通与物流工程学院1) 武汉 430063) (中交第二航务工程局有限公司2) 武汉 430012)

在中国西北地区存在大厚度、湿陷性较大的黄土,建设公路工程时,除了对黄土路基进行施工处理,更需要对其进行全方位的监测,以保证工程质量,且可通过沉降监测数据分析该路段的沉降规律,对预测后期沉降及最终沉降具有重要的意义.

目前,公路路基沉降预测通常采用曲线拟合法[1],拟合累计沉降量和时间的关系,从而算出趋于稳定的最终沉降量.曲线拟合法分为静态预测法和动态预测法[2],静态预测法包括双曲线法、指数曲线法、对数曲线法、星野法.动态预测法包括灰色预测法[3]和BP神经网络预测法[4].

文中依托TY15合同段20号桥台路桥过渡段黄土路基综合处治技术,分析加筋湿陷性黄土桥头路基的实测沉降,采用双曲线法、指数曲线法以及对数曲线法预测沉降,探讨其在该黄土路堤沉降预测中的适用性.

1 曲线拟合预测法理论

1.1 双曲线法

双曲线法[5]认为沉降量与时间按双曲线递减,其基本方程式为

St=S0+(t-t0)/[α+β(t-t0)]

(1)

式中:S0为拟合沉降量;St为时间t时的沉降量;α、β为待定参数.

当时间t趋于无穷大时,所对应的沉降量为最终沉降量S∞.

式(1)可改写为

(t-t0)/(St-S0)=α+β(t-t0)

(2)

式中:α和β分别为(t-t0)/(St-S0)～(t-t0)关系途中的截距和斜率,据此可以用图解法求出系数α和β.

将得到的α、β和S0、t0代入式(1),此时若已知任意时刻t则可以预估沉降量St.最终沉降量S∞可用式(3)求得.

S∞=S0+1/β

(3)

1.2 指数曲线法

指数曲线法[6]是根据不同条件下固结度的计算公式,某一时刻的沉降量用经验公式来表示:

生：3.14×6×6×8+3.14×6×6×（12-8）×应该是第二题的正确列式，第一题应该是3.14×6×6×12-3.14×6×6×（12-8）×

St=(1-αe-βt)×S∞

(4)

式中:St为地基土t时刻的沉降量;S∞为地基土的最终沉降量;α和β为由地基土的地质条件及排水条件确定的常数.

从实测沉降历时关系曲线上选择荷载停止施加后的3个时刻t1,t2和t3,并且使t2-t1=t3-t2,可推出指数曲线法的最终沉降量计算式为

(5)

式中:S∞为地基土的最终沉降量;S∞,S∞,S∞为地基停载后t1,t2,t3时刻的沉降量;t1,t2,t3为时间,且应满足t2-t1=t3-t2.

1.3 对数曲线法

对数曲线法[7]就是将已有的实测沉降量和时间的关系看作沉降量是随时间缓慢增加的对数曲线,因此,任意t时刻沉降量St的表达式为

St=a+blnt

(6)

式中:a,b为待定系数.

2 工程实例

甘肃某公路建设项目路基、桥涵及隧道工程施工TY15合同段,设计车速80 km/h,整体式路基宽度25.5 m,分离式路基宽度12.75 m,全线为湿陷性黄土路段.

针对TY15合同段20号桥台路桥过渡段路基沉降的监测横断面为K254+344,在距离桥台8 m处,也即为桥头搭板的尾端处,此为最易发生桥头跳车现象的位置,对其进行长期的沉降监测.其中沉降计编号1、2埋置于搭板下方,沉降计编号3、4埋置于回填路堤的中部,且沉降计1、3埋置于路肩侧,沉降计编号2、4埋置于路基中心侧,参考点沉降计设置在相应高度出的桥台处,具体沉降计布置方案,见图1.

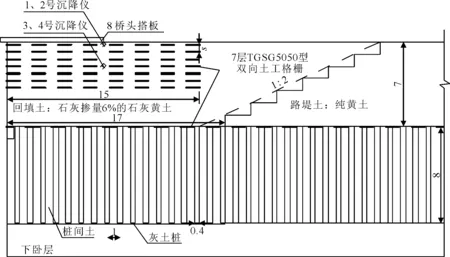
图1 沉降计布置图(单位:m)

TY15合同段20号桥台实际工程按照有限元分析的处治方案进行施工处理:采用地基打入8 m灰土桩,桩顶满铺1层TGSG5050型双向土工格栅,回填区采用石灰掺量为6%的石灰黄土回填,石灰黄土路堤上部铺设7层TGSG5050型双向土工格栅.沉降监测数据以2020年11月25日时监测数据为基准,当前采集止于2021年12月25日,采集得到的沉降数据绘制成沉降曲线,见图2.

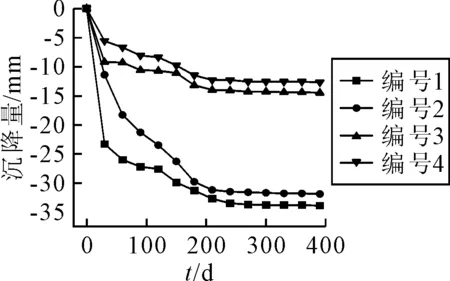
图2 K254+344断面监测沉降曲线

对4条监测沉降曲线进行整体分析变化趋势,曲线变化是很相似的.在0～50 d时,沉降速率很大,基本呈线性趋势进行快速沉降,沉降量能占到监测最大沉降量的75%;在50～200 d时,沉降速率逐渐减小,但沉降速率仍然较大;在200～300 d时,此时沉降速率较小,沉降速率进一步减小;而在超过300 d时,沉降曲线已经达到基本稳定状态,沉降值的变化很微弱.

2.1 沉降模型的建立

选取断面K254+344的编号1、编号2、编号3、编号4所采集的0～390 d的实测沉降数据,利用Origin软件分别针对双曲线、对数和指数3种模型进行非线性拟合,并计算出相关系数R2进行拟合效果的判断.

1) 双曲线模型拟合 断面K254+344四个测点0～390 d的实测数据,运用Origin双曲线拟合结果见图3.

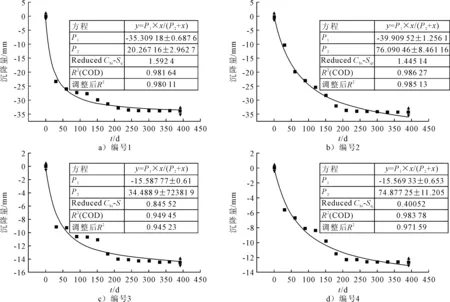
图3 编号1～4双曲线拟合图

由图3可知:编号2、4测点的拟合优度较好,拟合优度都大于0.96.

2) 指数曲线模型拟合 断面K254+344四个测点0～390 d的实测数据,运用Origin指数曲线拟合结果见图4.

图4 编号1～4指数曲线拟合图

由图4可知:编号2、4测点指数曲线拟合较好.

3) 对数曲线模型拟合 断面K254+344四个测点0～390 d的实测数据,运用Origin对数曲线拟合结果见图5.

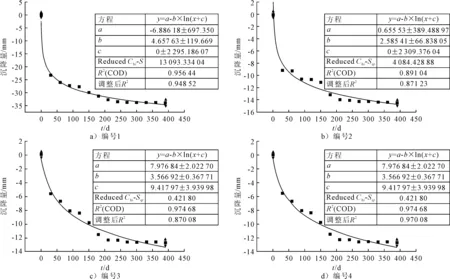
图5 编号1～4对数曲线拟合图

由图5可知:编号2、4测点的拟合优度较好.

对各编号沉降计的拟合模型进行分析可知:对于编号2、4的预测模型的三个拟合曲线的拟合度都很高,其三种预测模型的相关系数都大于0.96.而对于编号1,其拟合相关系数最小的为指数模型,也达到了0.93.编号3的沉降计拟合曲线的拟合效果相对就差很多,其指数模型和对数模型的相关系数均小于0.9.综上所述,对于路基的沉降预测模型,总体而言,指数、对数和双曲线模型都能进行较为精准的预测.

2.2 沉降预测模型的分析

以拟合较好的编号2沉降计为例,进行编号2预测模型值与监测值的对比分析,并利用各预测模型对路堤未来420、450、480、510、540、570、600、630、660、690、720、750、780、810 d的沉降值进行预测计算,编号2监测值与三种预测模型预测值曲线图,见图6.

图6 编号2监测值与3种预测模型预测值曲线图

由图6可知:道路中心线路基编号2沉降计的监测值在0～100 d时,路堤沉降速率很大;在100～200 d时,路堤沉降速率逐渐放缓;而在300 d后路基的沉降基本趋于稳定状态.对于选用的3种预测模型所预测的最终沉降值而言,指数模型最终预测值最小,在第810 d时,沉降值为32.63 mm;对数模型最终预测沉降值为37.23 mm;而双曲线模型最终预测沉降值为35.76 mm.而就三种预测模型的拟合程度而言,在0～200 d时,对数曲线与监测曲线的偏离程度较大,而指数曲线和双曲线曲线能在此时间段进行贴切的拟合;而在200 d后,则对数曲线和双曲线曲线都与监测曲线有较大的偏离,只有指数曲线能够较为贴切的进行拟合.因此,在三种预测模型中,首选指数预测模型进行沉降预测.

此外,运用SSE和MAPE两个评价指标对模型的预测精度进行评估,具体见表2.

表2 预测模型精度指标表

由表2可知:按照SSE评价指标,预测精度排序为:指数模型>双曲线模型>对数模型;3种沉降预测模型的MAPE均小于10%,精度均较高,预测精度排序为:指数模型>双曲线模型>对数模型.总上所述,沉降预测模型精度最高的是指数模型,精度最差的是对数模型.

3 结 论

1) K254+344断面不同测点的沉降曲线整体变化趋势是相近的,在0～100 d时,沉降速率很大;在100～200 d时,沉降速率逐渐减小;而在超过300 d时,沉降曲线达到基本稳定状态.

2) 针对K254+344断面编号2测点,双曲线、指数和对数预测模型都可以较为精确的预测路基的短期沉降量,就预测精度而言,根据误差平方和(SSE)平均绝对百分误差(MAPE)评价指标,指数模型最为精确.并运用指数模型预测最终沉降量为-32.63 mm.