基于Graph WaveNet模型的机场网络延误预测

姜 雨 戴垚宇 刘振宇 吴薇薇 顾 欣

(南京航空航天大学民航学院1) 南京 211106) (北京工业大学北京市交通工程重点实验室2) 北京 100124)

0 引 言

航班延误不仅会扰乱机场运行秩序,甚至可能波及整个机场网络,打乱航班计划,对机场和航空公司造成严重损失[1].准确可靠的航班延误预测是降低延误影响的关键,能够提高航班延误应对效率,为运行决策提供重要依据.

目前,国内外学者针对航班延误进行了一系列研究。王春政等[2]阐述了航班延误成因,并对现有延误预测研究进行系统性分类总结.传统方法、机器学习及深度学习等方法都广泛应用于航班延误预测研究.传统方法和机器学习研究中。罗赟骞等[3]以上游机场离港延误为输入,采用支持向量机建立延误模型预测下游航班的到港延误。郭野晨风等[4]针对恶劣气象条件引入天气影响交通指标(WITI),采用多元线性回归及BP神经网络建模进行机场延误预测。王语桐等[5]采用逐步回归算法和主成分分析法筛选影响延误的显著因素,基于支持向量回归和线性回归组合预测航班延误.深度学习研究中,Guvercin等[6]采用聚类模型对美国机场网络建模,选取典型机场进行延误预测。王春政等[7]面向机场网络各子系统交互作用下的延误特征涌现建立Agent模型,基于贝叶斯估计及模糊k阶邻域方法参数挖掘,并进行机场网络延误预测。吴仁彪等[8]引入注意力机制构建CBAM-CondenseNet模型,考虑延误波及影响进行航班延误预测。屈景怡等[9]提出基于区域残差和长短时记忆的深度学习模型,融合机场、气象及航班信息进行机场延误预测,预测精度优于传统算法.此外,航班延误对机场网络的波及传递影响近年来也备受关注.Baspinar等[10]采用传染病模型模拟航班延误发生、传播及恢复,分析航班延误的传播机理.Baspinar等[11]将排队网络模型应用于欧洲机场网络,模拟延误在网络中的传播,提出机场容量低于特定临界值时将导致延误激增.

以上研究多面向单一或数个机场进行延误预测,缺乏从机场网络角度考虑航班延误在机场间的传播影响.同时,深度学习模型普遍基于固定的网络结构挖掘空间关联性,易受不确定因素和数据不完全等干扰.而且现有研究实验数据集规模较小,在处理高维机场网络大数据时需要降维,易导致数据特征缺失。文中提出一种基于深度Graph WaveNet(GWN)模型的机场网络延误模型.GWN模型了融合时间卷积网络(temporal convolutional network,TCN)和图卷积网络(graph convolutional network,GCN),保留时间卷积网络并行计算、低内存等优势,高效处理高维延误数据,引入图卷积层挖掘空间关联性.GWN模型对机场网络整体建模,挖掘图结构化的航班延误信息,通过双向卷积捕捉航班延误传播规律,加入自适应邻接矩阵提升预测效果,对网络中所有机场进行多步延误预测.

1 模型建立

1.1 机场网络延误问题简述

机场网络延误预测问题的本质是时序预测问题.将机场网络抽象为一个有向权重图G=(V,E,A).V为含有N个机场节点的集合;E为机场之间连接关系的边的集合;A∈RN×N为预设权重的邻接矩阵,其中Aij用来表征由Vi机场至Vj机场的连接度.机场网络中,机场间的航线数量直接影响延误传播,因此选用机场间有向通航航线数量作为空间连接度指标.

时间窗口t中,机场网络的延误状态以动态的图信号Xt∈RN×D表示.采用多步延误预测,即基于已知的P个时间窗口的历史观察值和表征空间结构的图G递归预测未来Q个时间窗口的机场离港航班准点率.其映射关系为

(1)

式中:(Xt-P+1,…,Xt)∈RP×N×D,(Xt+1,…,Xt+Q)∈RQ×N×D.

1.2 空间卷积层

采用基于切比雪夫滤波器的一阶近似,通过对节点邻域信息进行聚合和变换来平滑节点信号,且适用于多维输入.图卷积层的定义为

Y=AWX

(2)

式中:Y∈RN×M为输出图信号;A∈RN×N为邻接矩阵;W∈RD×M为模型参数;X∈RN×D为含N个节点和D类特征的输入图信号.

上述模型的缺点是只适用于无向图结构.为抓取有向图的空间关联性,Li等[12]提出适用于有限k阶图信号的前向和后向扩散卷积.扩散卷积建模为

(3)

式中:Pk为转移矩阵的幂级数;K为扩散阶数.前向转移矩阵为Pf=A/rowsum(A),后向转移矩阵为Pb=AT/rowsum(AT).研究表明双向扩散卷积有效提高了预测模型的灵活性和有效性.

GWN模型引入自适应邻接矩阵Aapt,可视作隐性扩散过程中的转移矩阵,随机初始化之后,基于随机梯度下降原理,通过端对端的循环训练来挖掘隐藏的空间关联性.Aapt由两个随机初始化的可学习参数E1、E2组成的节点嵌入字典构成,表达式为

(4)

式中:E1为源节点嵌入参数;E2为目标节点嵌入参数.ReLU激活函数和SoftMax函数分别用于剔除不显著关联性的影响以及归一化处理.

空间卷积层由机场网络邻接矩阵Y和自适应邻接矩阵Aapt两部分构成.机场网络邻接矩阵通过k阶前向和后向扩散卷积捕获k阶空间关联性.自适应邻接矩阵用于捕捉网络的隐藏空间关联性.空间卷积层的结构见图1,表达式为

图1 空间卷积层结构

(5)

式中:Wk3为可学习参数矩阵.

1.3 时间卷积层

鉴于机场网络的复杂运行特性和超长时间序列数据输入,选择一维扩展因果卷积作为时间卷积层.通过跳过指定的输入步长,具备呈指数级扩大的感受野,结构示意图见图2.

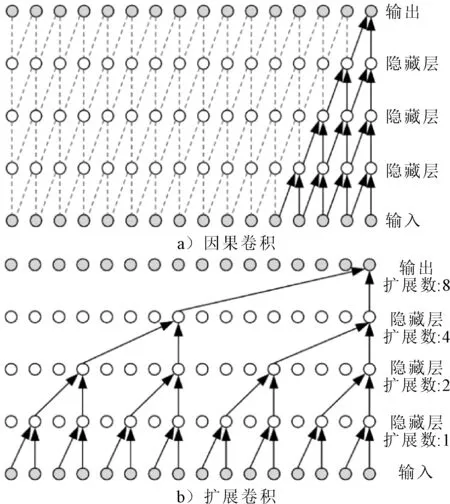
图2 因果卷积和扩展卷积结构

该模型用较少层数对长时序数据建模,有效缓解了梯度爆炸问题.用x∈RT表示一维序列输入,f∈RK表示卷积核,时间窗口t上的扩展因果卷积表达式为

(6)

式中:*为卷积运算;d为扩展因子;K为卷积核的尺寸.

门控机制是时间卷积网络的重要部分,能够有效控制信息流从进而影响卷积效果.时间卷积网络的门控策略为

h=g(Θ1*χ+b)⊙σ(Θ2*χ+c)

(7)

式中:χ∈RN×D×S为输入;Θ1,Θ2,b,c为模型参数;⊙为内积运算;g(·)为激活函数;σ(·)函数控制信息进入下一层的比例.选择正切双曲线的tanh函数作为激活函数g(·);sigmoid函数作为衰减因子σ(·)来控制各隐含层的信息流;g(·)和σ(·)统称为门控激活函数.

1.4 Graph WaveNet模型

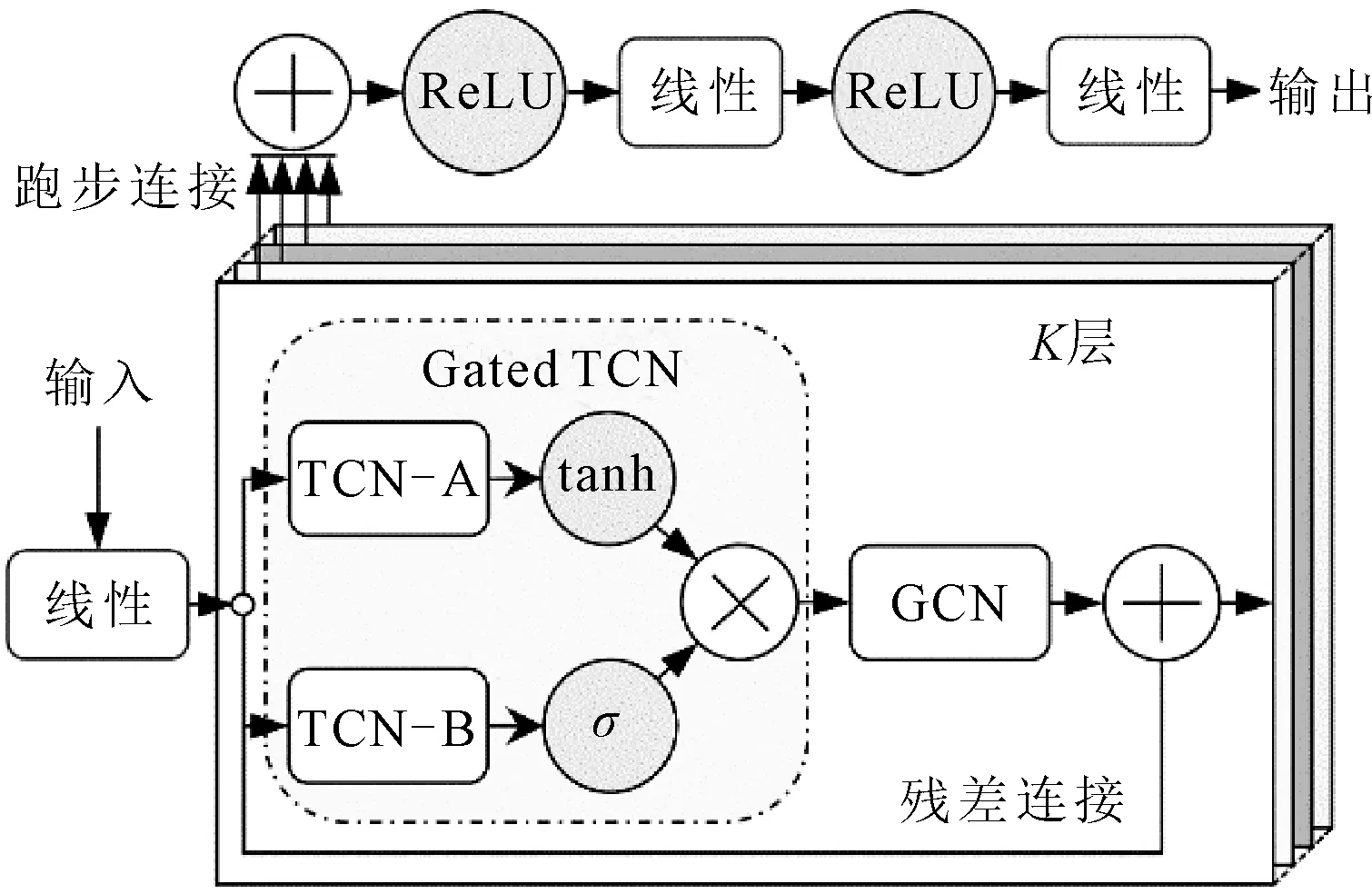
图3 Graph WaveNet模型结构

(8)

2 数据预处理与模型设置

2.1 数据预处理

选取美国年旅客吞吐量超过1000万人次的51个民用运输机场构建机场网络.机场延误数据取自联邦航空管理局(FAA)发布的航空系统性能指标(aviation system performance metrics,ASPM).样本数据囊括2011—2019年间3 287 d的实际机场运行信息,共167 637条.选择机场离港航班平均准点率作为延误指标,机场信息采集案例见表1.

表1 机场信息案例

航空公司通常每周制定航班计划,分别统计一周内机场网络中每个机场至其余50个机场的航班数量表示机场网络连接关系.航空公司数据同样源自美国联邦航空管理局.由于同一航线的往返航班频次存在差异,本文构建的机场网络是有向的、非严格对称的.基于机场网络抽象出以机场为节点,航线为边的有向图.表征有向图的权重邻接矩阵表示为

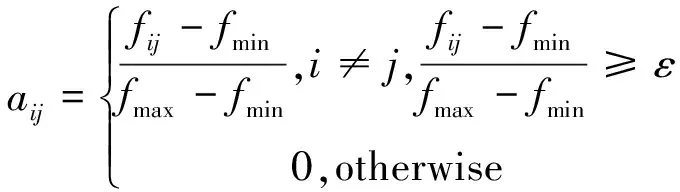
(9)

式中:aij为边的权重;fij为机场i与j间周航班频次;fmax和fmin分别为网络中每周航班频次最大值和最小值;ε为控制权重矩阵分布和稀疏性的阈值.

原始数据预处理步骤如下:①将所有延误数据聚合为以1 d为间隔形式,对缺失数据进行线性插值;②对输入数据进行Z-score归一化处理;③数据切片,前7年数据用于训练,第8年数据用于验证,第9年数据用于测试.

2.2 模型设置

所有深度学习模型都基于python 3.6版本运行,GWN模型使用Pytorch(1.1.0版本)实现,STGCN模型使用Tensorflow(1.9.0版本)实现.实验研究采用多步预测,基于7 d历史数据预测未来3d的机场离港航班准点率.GWN模型中,时空卷积块的数量设置为5,隐藏层数设置为8.模型共包括10层Graph WaveNet,扩展因子分别设为1,2,1,2,1,2,1,2,1,2.式(3)即为扩散阶数K=2的图卷积层.模型使用Adam优化器进行训练,初始学习率设定为0.02.为防止过度拟合,dropout rate设定为0.17,衰减速率设定为0.000 1.所有模型都进行50期的训练,批次大小设定为50.

选择4个深度神经网络模型作为基线模型,包括门控循环单元模型(GRU)、长短时记忆网络模型(LSTM)、堆叠式自动编码器(SAEs)和时空图卷积神经网络(STGCN).其中,时空图卷积神经网络为实验的主要基线模型.

2.3 评价指标

采用平均绝对误差(MAE)、平均绝对百分比误差(MARE)和均方根误差(RMSE)作为预测结果评价指标.MAE、MARE和RMSE的表达式为

(10)

(11)

(12)

3 结果与分析

3.1 预测结果分析

GWN模型和四个基线模型在三个评价指标下的预测表现见表2.表中预测指标为机场网络中所有机场预测结果的平均值.结果表明:预测第1天延误时,GWN模型的MAE较LSTM,SAEs,GRU,STGCN分别下降12.13%,8.32%,7.73%,1.93%;预测第2天延误时,MAE分别下降6.78%,7.25%,4.10%,2.45%;预测第3天延误时,MAE分别下降7.47%,13.27%,6.06%,4.20%.综合来看,GWN的预测性能在多数指标上表现最优,对未来第3天的预测精度显著优于其它模型,表明其在多步预测上具有突出优势.与STGCN相比,GWN对未来第1、2天的预测精度略优,对未来第3天的预测精度有显著提升,MAPE较STGCN提高0.2%.

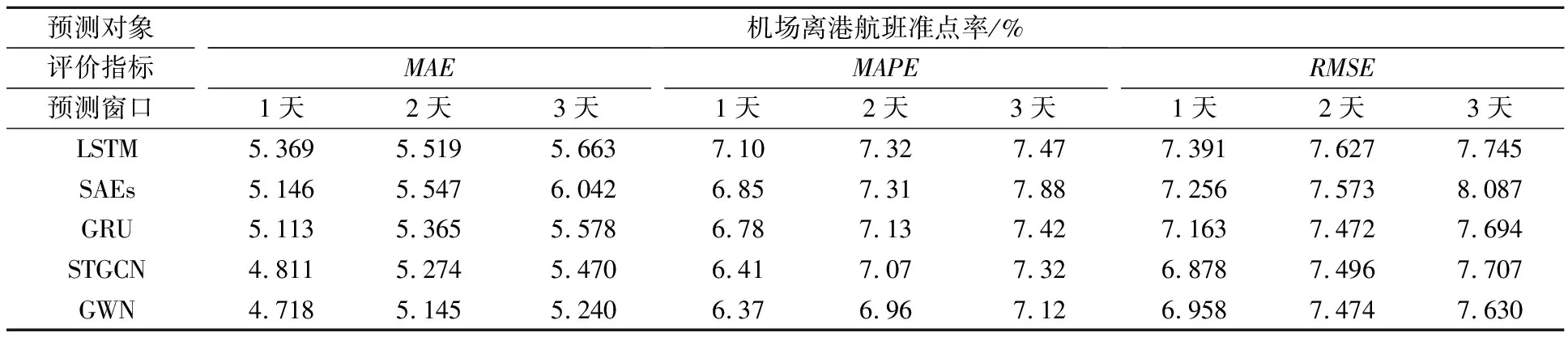
表2 多模型预测结果对比

图4为五种模型的预测误差箱型图.由图4可知:GWN的MAE和MAPE分布较其它模型更为集中,中位数优于大部分模型,仅MAPE中位数略高于STGCN.此外,GWN的上下四分位差IQR及预测误差上限显著优于其它模型,表明GWN在预测精度及稳定性上有显著优势.选取2019年9月1日—12月22日间历史数据及预测结果绘制折线图,见图5.由图5可知:离港航班准点率相对稳定时,各模型的预测结果接近;当准点率出现较大波动时,GWN在捕捉准点率波动峰值的表现上较STGCN更优,对数据变化趋势更敏感.综上,GWN预测表现优于其它基线模型,能够有效实现航班延误预测.

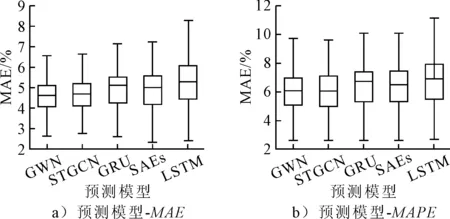
图4 预测模型误差箱型图

图5 预测结果曲线对比(第1天)

典型机场历史数据及预测结果对比见图6.所选机场包括檀香山国际机场(HNL)、盐湖城国际机场(SLC)、亚特兰大杰克逊国际机场(ATL)以及孟菲斯国际机场(MEM).HNL机场和SLC机场的MAE最小,分别为2.34%和2.64%.HNL机场预测误差小可归因于其地理位置远离美国本土,与其它机场连接度较低,因而机场网络中的延误传播影响被削弱.同理,位于阿拉斯加的安克雷奇国际机场的MAE也较低,为2.71%.SLC机场与HNL机场的年吞吐量相近,而该机场地处美国西部腹地,与机场网络连接度更高,因此延误波动更显著.ATL机场年吞吐量超1.1亿人·次,旅客中转率超过70%,网络连接度和重要度较高.ATL机场的MAE分别为4.81%,与整体MAE相近,表明GWN对大型枢纽机场同样具有稳定的预测表现.由图6可知:GWN能够准确预测准点率的波动趋势,然而对波峰波谷的预测精度有待提升.MEM机场MAE最大,达到10.91%,其本身是美国最大的货运枢纽机场,也是联邦快递的总部.MEM机场的离港航班准点率波动显著,同时航空货运对机场准点率影响较大,本文仅选取客运航班数据,导致预测误差较大.

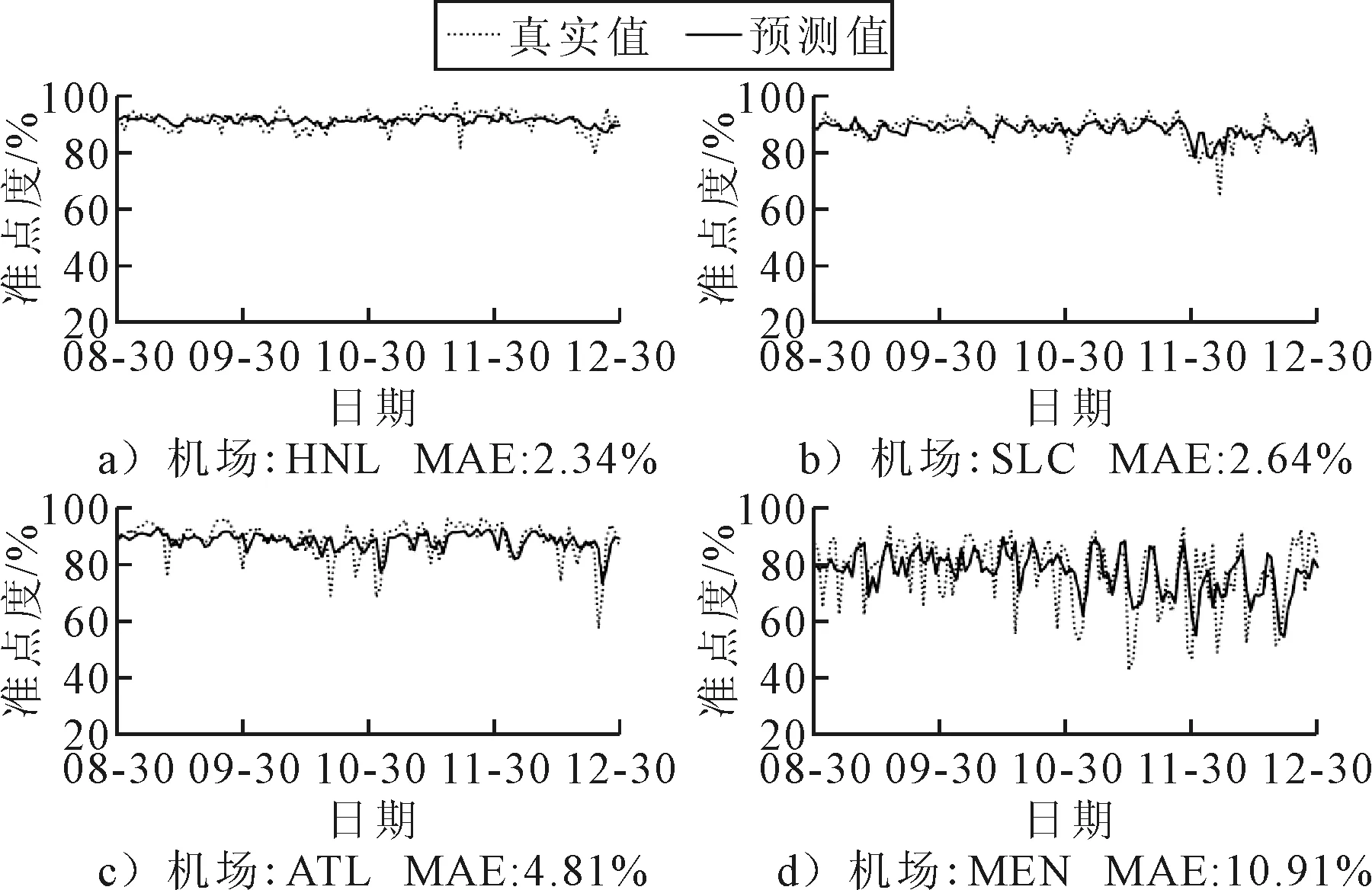
图6 典型机场GWN预测结果

GWN预测结果的正负误差分布见图7.51个机场中,29个机场的负误差天数多于正误差天数.正误差天数主要集中在160～180 d,而负误差天数主要集中于180～200 d.由此可见,GWN倾向于低估机场的离港航班准点率.结合预测曲线分析,GWN在机场出现严重延误时预测误差较大,导致负误差天数整体偏高.

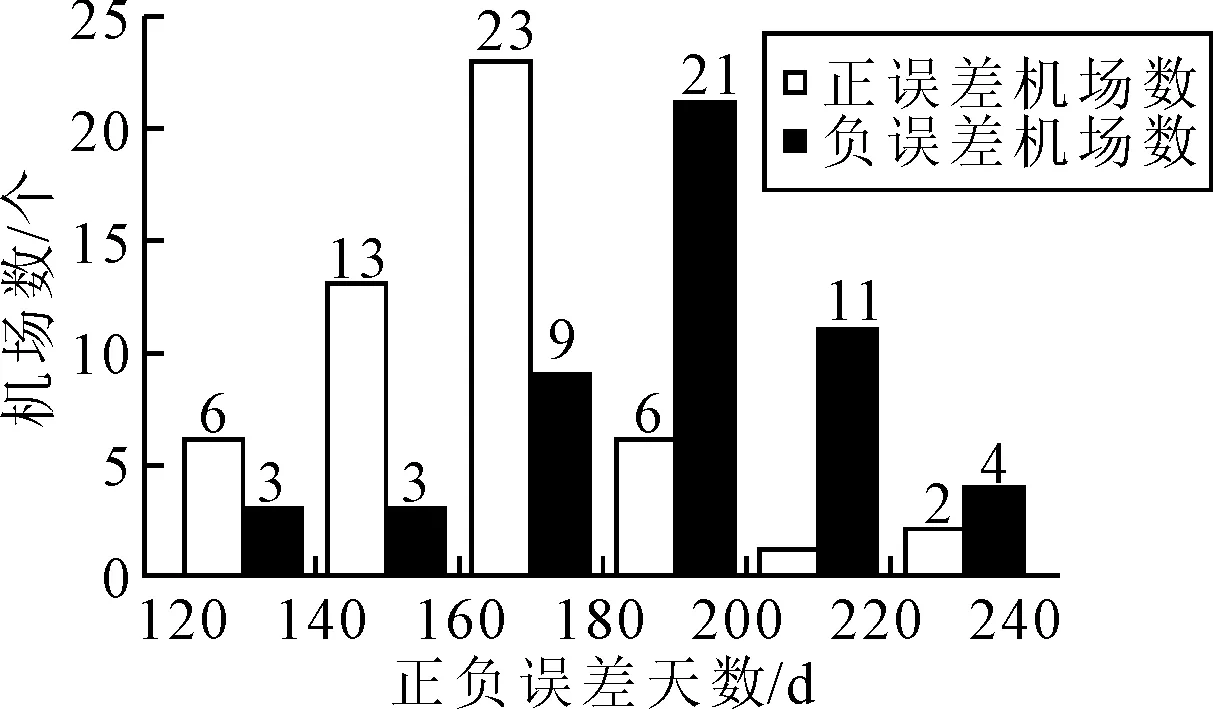
图7 GWN模型正负误差统计

3.2 灵敏度与邻接矩阵分析

实验对三个模型参数作灵敏度分析,包括最大扩散阶数K、时空卷积块数B以及隐藏层数H.实验中,随着扩散阶数K的增加,模型预测误差也逐步增大.当K设置较小时,卷积过程能够提取更多信息,同时也会造成计算工作量激增、过拟合等问题.实验结果表明,在K=2,B=5,H=8时,模型预测表现最佳.

实验对比5种邻接矩阵来验证空间卷积层构造的优越性.5种邻接矩阵构造对未来3天预测表现见图8.Identity、Forward、Apt、Bidir、Bidir_Apt分别为单位矩阵、基于预设权重矩阵作前向卷积、自适应邻接矩阵、基于预设权重矩阵作双向卷积以及融合双向卷积和自适应邻接矩阵.由图8可知:仅采用自适应矩阵的预测结果优于单向卷积,表明其能够有效挖掘隐藏的空间关联性.融合双向卷积与自适应邻接矩阵的空间卷积层预测表现最优,表明双向卷积矩阵能有效捕捉显性空间关联性,自适应邻接矩阵挖掘隐藏空间关联性,综合提高预测精度.

图8 邻接矩阵预测结果对比

4 结 束 语

文中提出一种基于深度Graph WaveNet的机场网络延误预测模型.GWN模型对机场网络整体建模,融合时间和空间卷积神经网络对网络中所有机场进行多步延误预测.时间卷积层中引入扩展因果卷积及门控机制,大幅缩短训练时间,有效解决梯度爆炸等问题,提升模型训练效率.其次,采用图卷积网络处理图结构化的机场网络延误数据,通过双向卷积和自适应邻接矩阵捕捉航班延误传播的显性和隐性空间关联性.结果表明:GWN模型的预测精度较其它基线模型有显著提升,在多步预测上具有突出优势,且对不同吞吐量级机场均有优越稳定的预测表现.