基于加速加载试验的沥青路面动力响应影响因素研究
黄 毅 郑炳锋
(湖南省交通科学研究院有限公司1) 长沙 410015) (苏交科集团股份有限公司2) 南京 211112)
0 引 言
动力响应反映了路面结构在移动荷载下的受力特性,可用来分析沥青路面服役期间性能演化规律,能够揭示路面损伤破坏机理.目前获取沥青路面动力响应的方法主要包括理论分析法[1-2]和实测法[3-4],但前者在力学模型、边界条件,以及材料参数等方面存在一定的局限性,导致不同模型计算得到的动力响应存在较大差别.后者采用足尺加速加载设备或真实车辆对预埋传感器的沥青路面进行测试,能够直接、准确地获得沥青路面动力响应数据.足尺加速加载试验是目前道路工程中最接近实际行车状况的试验手段,广泛应用于研究路面动力响应、疲劳及车辙模型以及长期性能演化规律[5-6].
采用加速加载系统对沥青路面动力响应的研究,Han等[7]采用HVS(heavy vehicle simulator)研究了倒装结构沥青路面的动力响应.Sha等[8]研究了四种路面结构动力响应随轴重、速度和温度的变化规律,并建立了沥青层底拉应变预估方程.文献[3]研究了沥青层底应变沿横向分布变化规律,发现沥青层底横向应变受荷载位置影响较大.文献[4]研究了轴重、车速和轮胎胎压对沥青层底应变和路基顶面应力的影响,并建立了动力响应回归方程.
文中基于交互作用正交设计,采用足尺加速加载设备MLS66(mobile load simulator 66)对预埋传感器的沥青路面进行不同工况下动力响应测试.通过极差分析和方差分析,得到各因素及其耦合作用对沥青路面动力响应的影响程度,分别建立了中、下面层底纵向拉应变和竖向压应变以及底基层底纵向拉应变的预估方程.
1 基于正交设计的加速加载试验
1.1 路面结构及传感器布设方案
在江苏省镇江市修筑长×宽为84 m×6 m的试验道,试验道设置2%的单向横坡及3‰的纵坡.试验道的路面结构采用江苏省高等级公路典型路面结构:上面层为4 cmSMA-13(SBS改性沥青),中面层为6cmSUP-20(SBS改性沥青),下面层为8cmSUP-25(70#道路石油沥青),基层为36 cm抗裂型水泥稳定碎石(水泥剂量4.5%),底基层为20 cm低剂量水泥稳定碎石(水泥剂量3.0%).路基填筑高度为120 cm(20 cm/层×6层),掺灰7%后逐层填筑压实.
在铺筑试验道过程中,在相应结构层分别埋设温度、应力及应变传感器,传感器型号及埋设层位见表1,传感器布设方案见图1.

图1 沥青路面传感器布设方案

表1 沥青路面预埋传感器型号
1.2 加速加载试验设计
MLS66可以实现六个加载轮进行单向循环加载,相较于HVS、ALF(accelerated loading facility)等其他加速加载设备的往复加载模式,MLS66能够更好地模拟实际车辆对路面的作用效果.加载速率上限为22 km/h,对应的每小时累计加载次数为6 000次.
参考文献[9],选择路面温度、轮重,以及速度作为影响因素,同时选取中面层底纵向应变、中面层底竖向应变、下面层底纵向应变、下面层底竖向应变和底基层底纵向应变五个目标参数.相较于单因素正交试验,相同水平数的交互正交试验的试验次数会大大增加.因此,每种因素仅选取两个水平,见表2.根据三因素二水平选择交互因素正交试验表L8(27),见表3.

表2 沥青路面动力响应交互正交试验因素及水平
根据表3中所列的工况进行试验,每种工况加载15 min,加载的同时对路面温度场及动力响应进行监测.监测得到的路面温度场见图2,根据沥青面层温度将其划分为低温和高温两个区域,其中中面层底(z=10 cm)低温和高温对应的温度范围分别是18~26、50~52 ℃;下面层底(z=18 cm)低温和高温对应的温度范围分别是16~20、39~40 ℃.

图2 沥青路面温度场
2 试验结果及分析
2.1 时程曲线
2.1.1中、下面层底
为方便应变分析,规定受拉状态为正,受压状态为负.将试验编号为#1、#3、#5、#7的中面层底应变时程曲线绘于图3.由图3可知:应变时程曲线呈现规律性周期变化,且不同工况对应的动应变幅值差距明显.
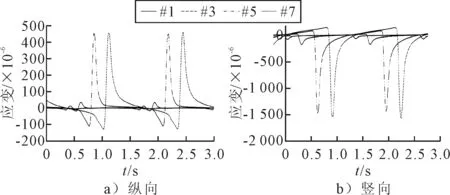
图3 中面层底应变时程曲线
2.1.2底基层底
将试验编号为#1、#3、#5、#7的底基层底纵向应变时程曲线结果绘于图4.由图4可知:底基层底纵向应变时程曲线在每个加载周期内均呈现受拉状态,当加载轮驶向传感器时,拉应变逐渐增大;当加载轮位于传感器正上方时,拉应变达到峰值;当加载轮驶离传感器时,拉应变逐渐减小至零.相较于中面层底应变,不同工况下底基层底应变幅值相差不显著.
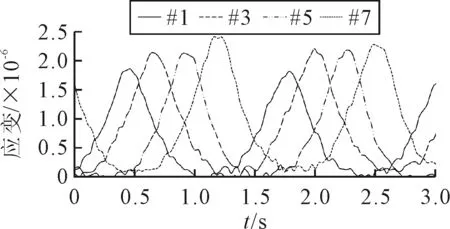
图4 底基层底纵向应变时程曲线
2.2 沥青路面动力响应影响因素研究
由于中、下面层底纵向应变时程曲线以拉应变为主,且沥青混合料层的疲劳开裂寿命预估方程大多是以沥青层底拉应变作为参数建立的,因此对纵向拉应变峰值εt进行分析.此外,由于沥青层内竖向应变时程曲线以压为主,且累计残余压应变会直接导致压密性车辙的产生,因此对竖向压应变峰值εc进行分析.表4为不同工况下动力响应实测结果,每种工况取48个加载周期,计算其平均值和标准差.

表4 沥青路面动力响应交互因素正交试验结果
2.2.1极差分析
极差能够反映因素对试验结果影响的大小,某种因素的极差越大,表明该因素越重要.因此,极差最大的因素即为最主要影响因素.表5为五个目标参数下不同影响因素的极差R,并对不同因素的极差进行排序并赋值,极差最大的因素赋值为6,依次递减,极差最小的因素赋值为1.图5为不同影响因素的极差排序,图中柱状高度越高,表明该因素的极差计算结果越大.

图5 不同影响因素极差排序

表5 不同影响因素的极差计算结果
对于中面层底纵向拉应变和竖向压应变,其路面温度的极差分别是348.9和1 181.1,高于下面层的40.7和373.5,这表明路面温度对中面层底动应变的影响大于下面层底.分析原因,随路面深度逐渐增加,向下传递的太阳辐射热量逐渐递减,进而导致下面层底温度变化幅度小于中面层底.由于沥青混合料是一种黏弹性材料,温度变化幅度越大,其自身模量变化范围亦越大,因此,在相同荷载水平下,应变变化范围越大.
中、下面层底纵向拉应变和竖向压应变的影响因素排序依次为:温度>速度>温度×速度,可见相较于轮重,温度、速度,以及其耦合作用对沥青层底纵向拉应变和竖向压应变的影响更大,其中路面温度是最主要影响因素.分析原因,当夏季高温时,沥青层的温度可升高至50~60 ℃,此时沥青混合料的模量显著降低,进而导致沥青层内纵向和竖向应变均显著增加.此外,根据时间-温度置换原理,加载频率的改变可以等效为温度的变化.具体说来,当车辆低速行驶时,其对沥青路面的作用频率降低,此时可以等效为沥青层温度升高,进而导致沥青层模量降低,沥青层应变增大.
不同工况底基层底拉应变变化范围较小,为(1.65~2.34) ×10-6,导致不同因素的极差值较为接近.其中轮重的极差为0.205,是影响无机结合料稳定层底纵向拉应变的最主要因素,其次是轮重与速度的耦合作用以及速度,温度则是影响底基层底拉应变的次要因素.这是由于底基层距路表较远,该层温度变化相对较小,且相较于沥青混合料,水泥稳定碎石自身的强度和模量受温度影响较低.高温条件下,沥青面层承载力降低,导致传递到无机结合料稳定层顶面的压力有所增加,进而间接影响了底基层底拉应变水平.
2.2.2方差分析
表6为五个目标参数下不同影响因素的方差计算结果.根据F检验的临界值表,当显著性水平α=0.05和α=0.1时,Fα分别为F0.05(1,7)=5.59和F0.1(1,7)=3.59.当某因素的F值大于F0.05(1,7)时,表明该因素对目标参数影响显著,标记为“**”;当某因素的F值大于F0.1(1,7)时,表明该因素对目标参数影响较为显著,标记为“*”;当某因素的F值小于F0.1(1,7)时,表明置信=90%时,该因素对目标参数影响不显著.

表6 不同影响因素的方差计算结果
由图6可知:对于中、下面层底纵向拉应变和竖向压应变,路面温度对应的F值均大于F0.05(1,7),表明路面温度对沥青层应变有显著影响(置信P=95%),其余因素影响均不显著.对于底基层底纵向拉应变来说,轮重对应的F值为1.638,高于其他因素,这一规律和极差分析一致.但所有因素的方差均小于F0.1(1,7),这表明当置信P=90%时,温度、轮重、速度及其耦合作用均为不显著的次要因素.
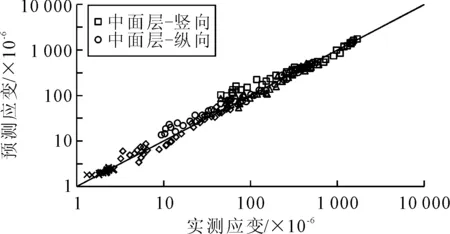
图6 应变实测值与预测值相关性
2.2.3预估方程
采用指数函数对中、下面层底纵向拉应变和竖向压应变及底基层底纵向拉应变进行回归拟合,并建立预估方程.
εt=a×eb×t-c×v+d×W
(1)
εc=-a×eb×t-c×v+d×W
(2)
式中:a、b、c、d均通过拟合得到;t为结构层所在深度的温度,℃;v为加载轮行驶速度,km/h;W为加载轮轮重,kN.
表7为拟合函数及其相关系数R2,图6为应变实测值与预测值的相关性.

表7 沥青路面应变峰值变拟合函数
中、下面层底应变回归方程中温度T对应的拟合系数b的范围为0.077~0.095,大于速度v对应的拟合系数c的范围0.025~0.044,而轮重W对应的拟合系数d最小,仅为0.001~0.009.这表明单位温度变化所引起的应变变化最大,其次为速度和轮重,这一规律和极差分析结果一致.
拟合精度结果表明,应变预估方程对中、下面层底应变状况有更好的适应性,其对应的相关系数R2均大于0.96;而底基层底拉应变回归方程的相对系数R2相对较低,仅为0.78.在后续的研究中关于底基层底拉应变预估方程的构建尚需要引入路基湿度、模量等相关参数,以提高预估方程的精度.
3 结 论
1) 路面温度是影响中、下面层底应变的最主要因素,其次为速度和温度与速度的耦合作用,轮重对中、下面层底纵向拉应变和竖向压应变影响相对较小.对底基层底拉应变影响较大的因素是轮重.
2) 建立了以路面温度、轮重、速度为参数的沥青路面动应变预估方程,指数函数的应变方程对中、下面层底应变具有较好适应性,相关系数R2均大于0.96.为后续研究沥青路面动力响应随累计轴次的变化提供了支撑,可采用预估方程对不同工况下应变幅值进行归一化处理,以便消除温度、荷载等因素的影响.

