异步性温度变化下斜拉桥上列车走行性研究

戴公连，肖尧，王芬，葛浩，饶惠明

(1.中南大学 土木工程学院，湖南 长沙 410075；2.长江勘测规划设计研究有限责任公司，湖北 武汉 430010；3.东南沿海铁路福建有限责任公司，福建 福州 350013)

斜拉桥跨径大，跨越能力强，在跨越山区、河流、海湾或者既有线路和航道时成为理想桥型之一[1]。在环境温度作用下，桥梁结构将产生温度变化，引起应力和变形，其大小与大气温度、结构形式和材料类型等密切相关[2-6]。过大的主梁温度变形会使高速铁路轨道的几何形位产生不利变化，进而影响列车的安全运行。目前，对斜拉桥温度场的研究还仅限于不同构件单独的温度变化规律及温度模式。丁幼亮等[7]对公铁两用斜拉桥的主梁进行温度和挠度的长期监测，将挠度数据进行小波变换，分离出来温度、列车荷载和汽车荷载各自引起的挠度，讨论研究温度挠度的时频特征和列车挠度的概率统计特征。戴公连等[8-9]对大跨度斜拉桥的拉索和主梁温度模式分别进行研究，利用山区斜拉桥拉索节段模型的短期温度监测数据，基于最大熵原理预测了50 a 及100 a 重现期下的拉索温度极值；以沿海斜拉桥的主梁温度实测数据建立升温和降温下的主梁温度时程模型，并提出一种钢混结合梁温度场的高效有限元模型。许翔等[10]利用监测得到的钢箱梁斜拉桥温度数据分别研究了钢箱梁和索塔的温度梯度，并基于广义帕累托模型预测100 a 重现期下的温度作用极值。周浩等[11]基于大跨度结合梁斜拉桥的主梁、桥塔和拉索温度监测数据，分析得出主梁、桥塔单独的竖向温度梯度及索梁、索塔各自的温差计算模式。众多学者在斜拉桥上建立健康监测系统，对各构件展开温度监测和研究[12-14]。目前对温度作用下的斜拉桥车桥耦合振动研究多仅考虑桥梁的整体升降温[15]。但斜拉桥结构较为复杂，主梁、桥塔和拉索作为其主要构件，组成材料并不相同，导热能力也有所不同，因此各构件的温度变化幅度和规律并不完全一致。若不考虑各构件温度变化的非一致性，将导致斜拉桥的温度变形计算与预测不准确，使得列车走行性分析出现误差。因此本文根据泉州湾大桥主梁、桥塔和拉索的1 a 实测温度数据，分别整理其年变化和日变化时程规律，统计分析不同温度分量的温度变化异步性。建立Ansys 有限元模型研究异步性温度分量组合下的主梁变形，基于弹性系统动力学总势能不变值原理[16]建立车桥耦合振动模型，研究异步性温度变化对列车走行性的影响。

1 试验概述

1.1 试验对象

以新建福州至厦门客运专线的泉州湾跨海特大桥的主桥为研究对象。泉州湾跨海特大桥全长20.287 km，主桥采用(70+130+400+130+70) m 双塔双索面钢混组合梁斜拉桥桥型。桥梁各构件参数为：主梁宽不含风嘴为17 m，含风嘴为21 m，梁高4.25 m，桥面板混凝土型号为C55，钢箱梁钢材型号为Q370qE；主塔为H 型桥塔，混凝土型号为C50，总塔高约为160 m，高跨比1/3.67；斜拉索为镀锌平行钢丝拉索，共72 对。泉州湾跨海特大桥主桥布置图见图1。

1.2 试验方案

研究对象地处近海环境，易受温度因素影响，极端条件下当地气温最值分别可达到0.3 ℃和38.9 ℃[17]。在环境温度作用下，斜拉桥各部件温度场变化复杂，且变化时程规律并不一致，这对分析和预测大跨度斜拉桥的温度及其变形带来了障碍。考虑到主梁、桥塔和拉索均为细长结构，同一构件的不同截面温度可近似认为相同，因此在泉州湾跨海斜拉桥的主梁及靠南侧的一个桥塔选定一典型截面布置温度监控系统，在靠近泉州湾附近的一处开阔地设置拉索节段模型试验，以获得主梁、桥塔和拉索的实时温度数据，研究大跨度斜拉桥各个构件的温度时程变化规律。在桥塔、主梁跨中及梁端各设置了一个位移传感器，获得各对应截面的位移以验证本文变形分析的准确性。各个构件的温度测点布置示意图见图1，图中Pb,c和Pb,s分别为主梁混凝土部分和钢箱梁部分展示测点，Pt为桥塔展示测点，Pc为拉索展示测点，这4个展示测点的数据用于后文展示实测温度原始数据。

2 斜拉桥各构件温度变化规律分析

对温度实测数据进行处理后得到结构的均匀温度和线性温差。对于钢混组合结构的主梁而言，假设其截面在变形时依然维持平截面，且钢和混凝土线膨胀系数保持一致，推导结构离散温度场的均匀温度和线性温差的计算式如下[18-19]：

式中：Tu，Tv分别代表结构的均匀温度分量和线性温差分量；Ei，Ti，Ai，zi分别代表每个温度测点有效分割区域对应的弹性模量、温度测量值、面积和形心相对于截面主惯性轴的坐标；D为截面高度。单一材质的桥塔和拉索应用式(1)或式(2)处理温度数据时可不考虑弹性模量Ei影响，式中Ei可省去。

2.1 年周期变化规律分析

桥塔温度测点从2020 年1 月开始工作，拉索节段模型的温度测点从2020 年9 月开始工作，主梁温度测点从2021 年3 月开始工作，各个测点每0.5 h 测量一次温度并存储。为保证一致性，以主梁温度数据时间长度为基准，选取2021 年3 月17日到2022 年3 月17 日这一段时间进行分析。将各构件展示测点的原始温度时程曲线绘制成图2。

从图2中可知，混凝土桥面板和拉索的测点直接承受阳光照射，日温度波动幅度较大；钢箱梁和桥塔的测点没有受到阳光的直射，日温度波动幅度很小。

将各构件测点的温度数据代入式(1)或式(2)进行计算，对应时刻的大气温度Ta及得到的计算结果见图3。图中Tb,u代表主梁均匀温度分量，Tt,u代表桥塔均匀温度分量，Tc,u代表拉索均匀温度分量，Tb,v代表主梁沿截面高度的线性温差分量，Tt,l代表桥塔顺桥向线性温差分量，Tt,t代表桥塔横桥向线性温差分量，Fb,u代表主梁均匀温度的拟合曲线，Ft,u代表桥塔均匀温度的拟合曲线，Fc,u代表拉索均匀温度的拟合曲线，Fb,v代表主梁线性温差的拟合曲线。

由图3 可知，Tt,l和Tt,t仅有小幅度温度波动，对主梁的温度变形不会造成太大影响，后续将不再分析；Tb,u，Tt,u，Tc,u和Tb,v表现出季节性变化的特点，均以年为周期近似按余弦曲线变化，可采用傅里叶级数对其进行拟合，得到各温度分量的表达式：

式中：Ti为构件的温度分量，℃；t为日序数，从1月1 日算起；TA，TW和t0为拟合参数，不同温度分量的拟合结果如表1所示。

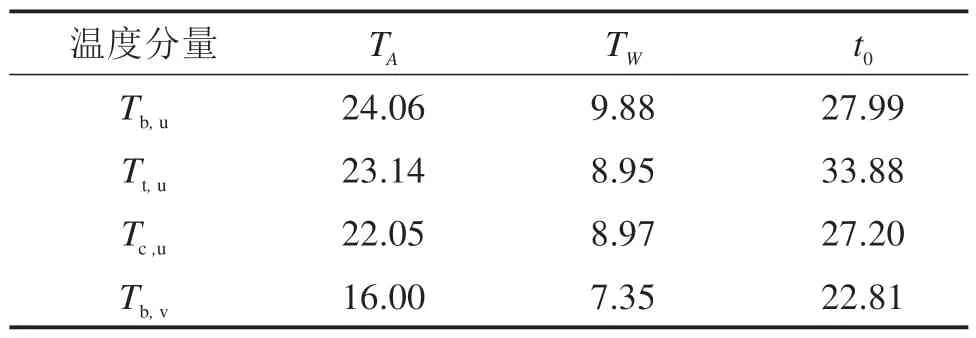
表1 拟合参数Table 1 Fitting parameters

各个温度分量的年最值出现时刻及对应值如表2 所示。虽然图3 的拟合结果显示Tb,u，Tt,u，Tc,u和Tb,v总体变化趋势有相似性，但不同温度分量的拟合参数有一定差距。从表2的年最值统计中不难看出，不同温度分量的年波动幅度、年最值出现时间及大小并不一致。

表2 温度分量年最值统计Table 2 Annual maximum value of temperature components

2.2 日周期变化规律分析

3 个构件的温度分量和大气温度在太阳辐射作用下的日周期变化规律主要符合正常波动和持续降温这2 种模式。选取2 种模式的典型天气条件，2021 年5 月20 日和2021 年3 月21 日的数据进行 分析，如图4 所示。正常波动模式下，Tb,u，Tt,u，Tc,u和Tb,v近似按余弦曲线变化，可采用傅里叶级数对其进行拟合，如式(4)；持续降温模式下，大气温度和结构温度分量均呈现直线下降，可采用线性公式进行拟合获得其时程函数，如式(5)。

图4 温度分量日变化Fig.4 Diurnal variation of temperature components

式中：Ti,A和Ti,W分别代表对应温度分量的日平均值和波动幅值；τ代表时刻，h；τ0代表温度分量最值的发生时刻；Ti,max和Ti,min分别代表对应温度分量的日最大值和日最小值。

由图4可知，在5月20日，温度分量正常波动的情况下，Tb,u日变化幅度为2.09 ℃，Tt,u日变化幅度为0.47 ℃，Tc,u日变化幅度为5.10 ℃，Tb,v日变化幅度为2.56 ℃。Tb,u日最大值出现在17:00，日最小值出现在6:30；Tt,u日最大值出现在17:00，日最小值出现在6:00；Tc,u日最大值出现在14:00，日最小值出现在6:00；Tb,v日最大值出现在17:00，日最小值出现在9:00。因此，不同温度分量的日波动幅度和日最值出现时刻也存在异步性。在3 月21 日，温度分量持续下降的情况下，不同温度分量均同步到达最值。将一年中3个构件的均匀温度每天达到日最值的时刻进行统计并绘于图5中。

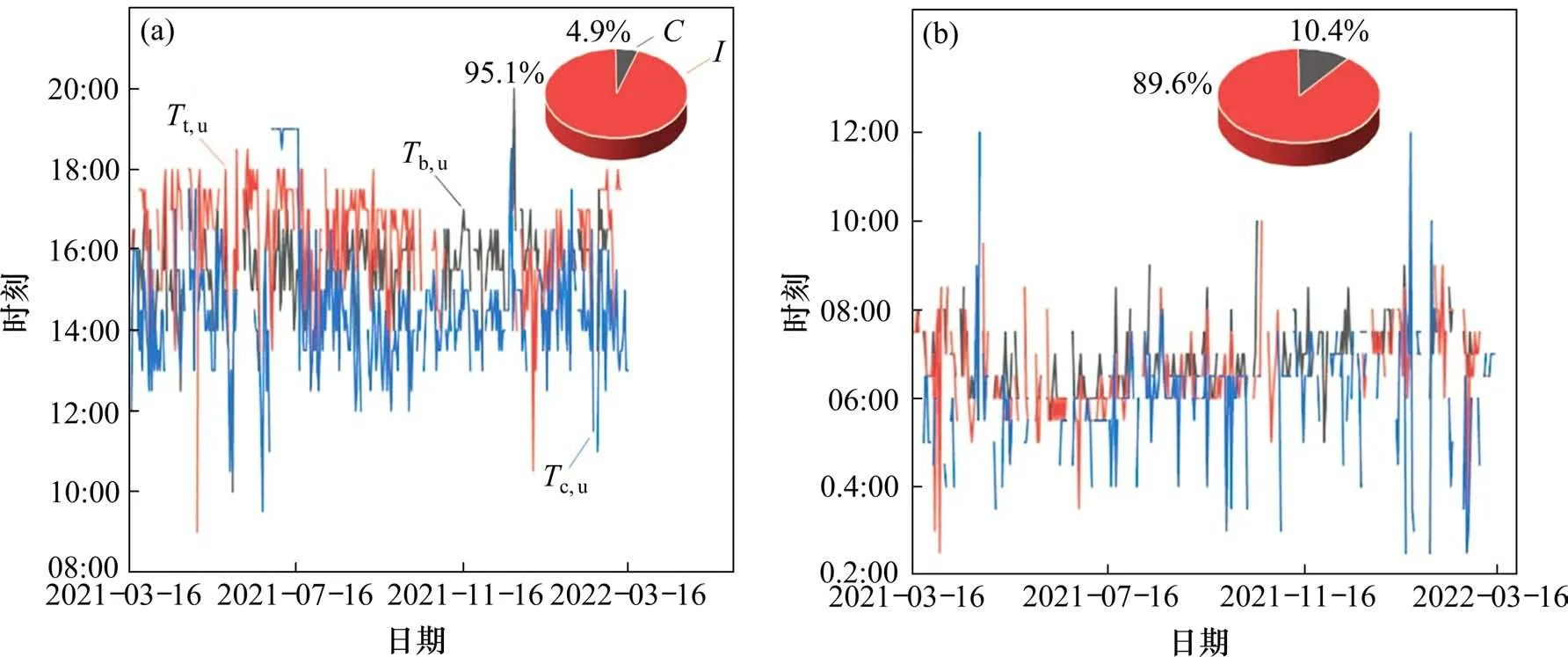
图5 日最值出现时刻Fig.5 Occurrence time of daily maximum

图5中饼图为一年中Tb,u，Tt,u和Tc,u日最值出现时刻一致和非一致的天数的比例，C代表日最值出现时刻一致的天数，I代表日最值出现时刻不一致的天数。由图5中可知，不同温度分量在一年中的大部分时间里都表现出了异步性。

综上，由于各个构件的材料及其导热性能不同，实际上各自的温度历程总是有些微差别，温度变化幅度不尽相同，难以同步达到最值。若不考虑实际温度变化中表现出来的异步性，按照传统的不同构件的温度极值简单叠加或者整个体系的升降温对温度变形进行计算和预测，将不可避免地产生误差，继而影响对列车走行性的正确评估。

3 异步性温度变化下斜拉桥温度变形

3.1 实测位移数据对比

使用Ansys软件建立全桥有限元模型，计算实测温度时程下的温度变形，与实测跨中竖向位移、梁端纵向位移和桥塔双轴倾角时程数据进行对比。斜拉桥的有限元模型采用“鱼骨梁”模型建立，主梁及桥塔以beam189 单元建立模型，拉索以link180 单元建立模型，拉索与主梁的连接用mpc184 单元模拟，桥梁模型的边界约束条件用combin14 单元模拟，各构件的截面尺寸及材料特性按前述参数取定。连接墩、辅助墩处设立竖向约束和横向约束，保持纵向活动；桥塔和主梁间设竖向约束和横向约束，纵向设带限位功能的粘滞阻尼器[20]。建立的模型如图6所示。

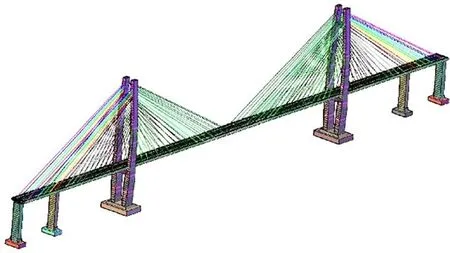
图6 有限元模型示意图Fig.6 Schematic diagram of finite element model

主梁合龙时间为2021 年8 月6 日15:00 左右，根据实测数据，此时的Tb,u为26.88 ℃，Tt,u为28.58 ℃，Tc,u为26.10 ℃，Tb,v为16.15 ℃，Tt,l为0.27 ℃，Tt,t为0.11 ℃，模型的初始温度据此进行设置。有限元计算结果与实测位移时程数据的对比如图7 所示，图中标记点为位移测点位置，dl，dv，rl和rt分别代表主梁梁端纵向位移，主梁跨中竖向位移，桥塔测点位置的绕顺桥向转角和绕横桥向转角。

图7 实测位移时程曲线对比Fig.7 Comparison of measured displacement time history curves

由图7 可知，3 个测点的计算值和实测值时程曲线基本一致。上述对比证明有限元模型能准确反映温度变化导致的变形，满足本文分析需求。

3.2 异步性温度变化对主梁温度变形的影响

基于前述Ansys模型研究异步性温度变化对主梁温度变形的影响，选择Tb,u，Tt,u，Tc,u和Tb,v分别单独达到年最大值时刻的工况1～4，或年最小值时刻的工况5～8 进行研究，并考虑各个温度分量最值叠加的工况9 和工况10，以及假设Tb,u，Tt,u，Tc,u均升温10 ℃和降温20 ℃的工况11 和工况12 作为对比工况。整体升降温工况11 和工况12 中升降温幅度接近于实测1 年内的升降温幅度，相应的Tb,v，Tt,l和Tt,t均取为实测数据中工况11 和工况12的Tb,u和Tt,u取值的对应值。将各个工况对应的温度分量输入到模型中进行计算分析，各个工况的温度分量值如表3所示。

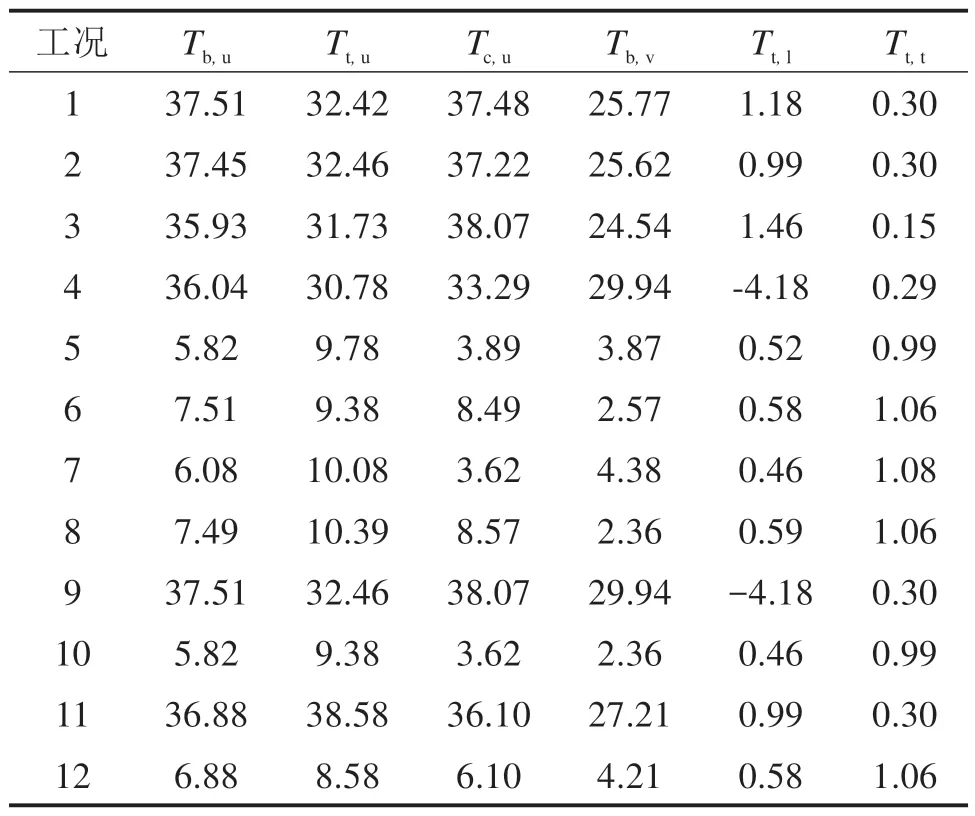
表3 温度分量计算工况表Table 3 Temperature component calculation table ℃

计算结果如图8所示，图中数字表示对应变形曲线的工况序号。从图8中可以看出，由于边跨跨度较小，不同升温工况和不同降温工况的温度变形均十分接近，基本不受异步性温度变化的影响；主跨跨径400 m，其温度变形在不同工况下差异显著，受异步性温度变化影响明显。工况3(拉索温度达到年最大值)和工况7(拉索温度达到年最小值)可将所有计算工况的温度变形曲线包络。温度分量年最大值叠加的工况9 下主跨跨中变形比工况3小1.47 cm；温度分量年最小值叠加的工况10 下主跨跨中变形比工况7 小0.52 cm；整体升温的工况11 下主跨跨中变形比工况4 小0.71 cm；整体降温的工况12 下主跨跨中变形比工况7 小2.07 cm。因此，若不考虑温度变化的异步性，基于不同构件温度极值的简单叠加或桥梁结构整体升降温来研究斜拉桥的温度变形，得到的结果将小于其真实温度变形。

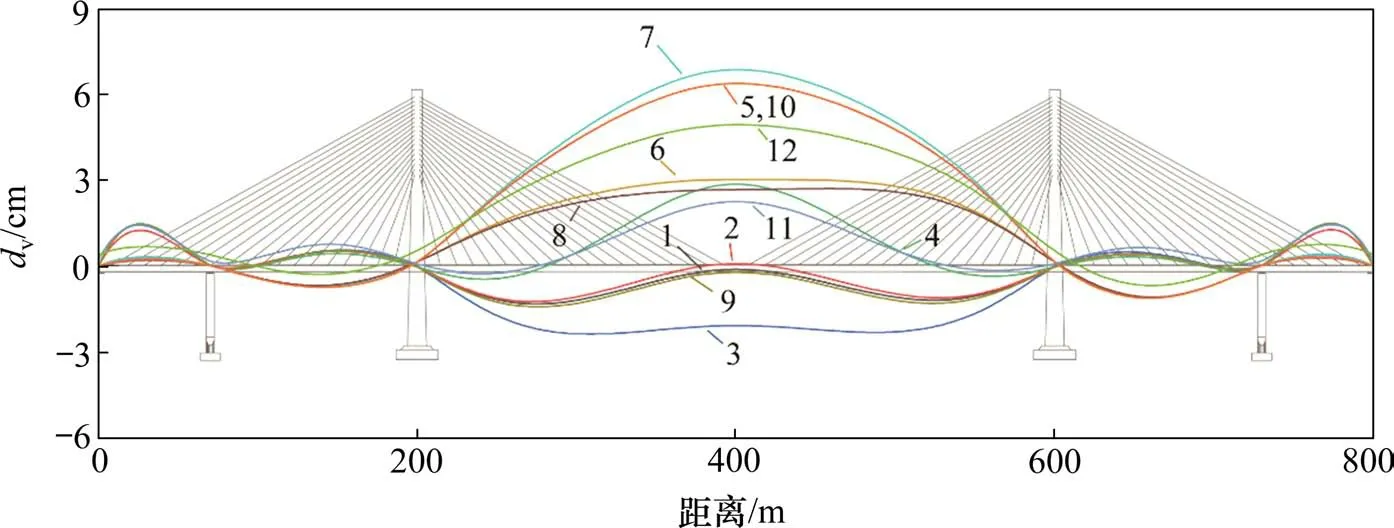
图8 主梁温度变形计算结果Fig.8 Calculation results of temperature deformation of main beam

4 考虑异步性温度变化的列车走行性分析

4.1 车桥耦合振动模型

根据弹性系统动力学总势能不变值原理和形成矩阵的“对号入座”法则编写车桥耦合振动计算程序Train-Track-Bridge(TTB)，建立车桥系统时变模型。桥梁模型的主梁、桥塔、桥墩和桩基均采用空间梁单元建模，拉索采用空间杆单元建模，基于m 法考虑桩土之间的共同作用。列车模型的车体、轮对和转向架被简化为刚体，并且考虑车体和转向架的侧滚、侧摆、点头、摇头和浮沉运动，以及轮对的侧摆和摇头运动；弹簧及蠕滑力均按线性计算，阻尼均按黏滞阻尼计算，轮轨接触模型为密贴模型。最终得到按二系弹簧计算的23自由度四轴列车模型。

该车桥时变系统的矩阵方程可以表示如下：

式中：K，C，M分别表示系统的刚度、阻尼及质量矩阵；δ，，分别表示系统的位移、速度和加速度列阵；P表示系统的外荷载列阵。

将不平顺激励及温度变化引起的主梁变形代入式(6)，再使用逐步积分法即可求解车桥系统耦合振动响应。依据上述原理建立的车桥耦合振动模型如图9所示。

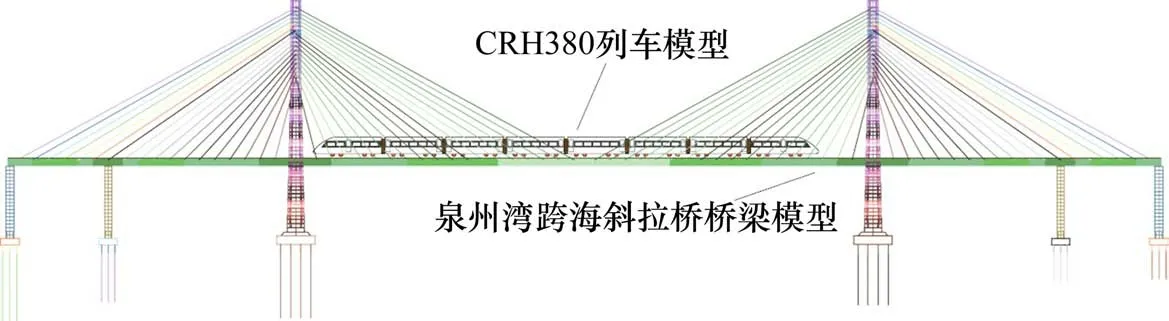
图9 车桥耦合空间振动分析模型Fig.9 Analysis model of vehicle bridge coupling spatial vibration

4.2 异步性温度变化影响下的列车走行性分析

假定轨道与主梁变形相同，将工况1～12下的主梁温度变形曲线叠加进原始轨道不平顺，形成等效轨道不平顺作为车桥耦合系统的激励，其中原始轨道不平顺由德国低干扰轨道谱随机生成，等效轨道不平顺如图10 所示，图中0 代表的曲线为原始轨道不平顺。模拟计算前述12 个工况以及不考虑温度变形的工况13 下单线CRH380 列车分别以250，300，350和400 km/h速度经过桥梁时的列车动力响应，列车编组为1×拖车+6×动车+1×拖车。得到的第1节列车的安全性及舒适性动力响应指标结果在4 个速度中的最大值均满足文献[21]中的规定，具体数值如表4所示。

图10 轨道不平顺幅值Fig.10 Amplitude of track irregularity

从表4中可以看出，当温度变化时，列车竖向加速度指标有明显的增加，但在温度分量有较大差别的工况下增加幅度不尽相同。工况13 的竖向加速度为0.97 m/s2；在升温情形下，工况3 的竖向加速度达到最大值，为1.10 m/s2；在降温情形下，工况7 的竖向加速度达到最大值，为1.07 m/s2。而最不利工况3 和7 均是仅拉索达到年最值时的温度分量组合，因此拉索的温度变化对列车走行性有较大的影响。将工况3，9，11以及工况7，10，12的计算结果绘于图11，从图中可知，考虑温度分量年最值叠加及桥梁结构整体升降温时的列车竖向加速度在各计算车速下均小于仅拉索均温分量达到年最值时的结果。综上，斜拉桥车桥耦合振动也受到温度异步性变化的影响，不考虑该影响时，列车竖向加速度要比真实最不利情况下的对应值小。

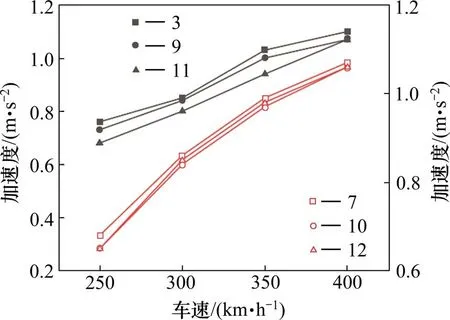
图11 列车竖向加速度对比Fig.11 Comparison of vertical acceleration of train

5 结论

1) 主梁的均匀温度分量Tb,u，线性温差分量Tb,v，桥塔和拉索的均匀温度分量Tt,u和Tc,u的年变化幅度均较大但并不一致，可用傅里叶级数进行拟合，且拟合公式中不同温度分量的拟合参数也不一致，拟合通式可归纳为Ti(t)=TA-TWcos[2π(tt0)/365]。桥塔的顺桥向和横桥向线性温差分量Tt,l和Tt,t年变化幅度极小，可忽视其对斜拉桥主梁温度变形的影响。

2)Tb,u，Tt,u，Tc,u和Tb,v的日变化规律在大气温度正常波动天气条件下可用傅里叶级数拟合，拟合公式中不同温度分量的拟合参数不一致，通式可归纳为Ti(τ)=Ti,A-Ti,Wcos(2π(τ-τ0)/24)；在大气温度持续下降的天气条件下可采用线性公式进行拟合。在一年中大部分时间不同构件均温分量不能同步到达日最值，且温度变化幅度也不一致，斜拉桥各构件的温度变化表现出显著异步性。

3) 利用基于实测位移数据验证的Ansys模型计算考虑异步性温度变化的主梁温度变形，结果表明不同温度分量年最值叠加及桥梁结构整体升降温时的变形小于考虑异步性温度变化时的变形，即若不考虑异步性温度变化，得到的主梁温度变形曲线将无法包络真实温度作用下的主梁变形。

4) 列车动力响应受到异步性温度变化的影响，若不考虑该影响，计算得到的列车竖向加速度将偏小，评估结果会偏于安全。建议进行斜拉桥上列车走行性分析时考虑不同构件异步性温度变化的影响。