新型柔性铰接框架锚固体系及边坡支护分析

李翔宇 ，王海军，徐 玮，汤 雷，王 倩

(1.中国矿业大学 江苏省土木工程环境灾变与结构可靠性重点实验室，江苏 徐州 221116；2.南京水利科学研究院，江苏 南京 210029；3.苏交科集团股份有限公司，江苏 南京 210019；4.德州市陵城区水利局，山东 德州 253500)

近年来的边坡防护研究，在现代支护原理的基础上提出了框架预应力锚杆支护结构[1]。锚杆支护结构既可限制边坡表面土体过大变形而出现松动现象，又可控制边坡深层滑动位移。在工程造价和社会效益方面，框架预应力锚杆支护比传统的支护加固抗滑结构更具优势。

在边坡支护领域框架预应力锚杆支护结构应用日益广泛的大背景下，国内外研究人员对框架预应力锚杆结构的作用原理及其在工程实践中的应用通过数值仿真模拟、模型试验、现场试验等手段进行深入研究。作为较早采用的工程加固方式，锚杆锚固的相关研究也较多。早期Keuser 等[2]把锚杆简化为梁单元或桁架单元进行计算，这种方法虽然计算简单但难以反映灌浆的作用，与工程实际并不相符。随后Hollingshead 等[3-4]学者提出了考虑灌浆影响的方法。这些关于锚杆理论的多方面研究，为日后框架预应力锚杆支护结构设计理论打下了基础。国内许多学者也对框架预应力锚杆支护结构的进一步探索贡献良多。贾金青等[5]利用数值分析方法研究了边坡的变形与滑移场理论，并对比了相同条件下土钉的支护效果；潘晓娟[6]根据框架锚杆支护体系的作用机理，提出一种框架预应力锚杆支护边坡的简化计算模型，将锚杆所受轴力假设由边坡土体产生的侧向土压力和后期施加的预应力两部分组成；王邓峮[7]基于圆弧滑动破坏，把预应力作为集中力作用于滑体上，得出一种框架预应力锚杆支护边坡稳定性分析计算的简化方法，并采用Matlab 编程，实现最危险滑移面搜索过程的可视化；唐仁华等[8]将框架梁在张拉阶段和工作阶段不同破坏下的失效模式视为串联系统，提出了框架预应力锚杆的分阶段系统可靠性计算模型，分别计算其内力，得出预应力框架失效概率的原因和概率；庄超[9]针对深基坑工程施工场地狭窄和存在回填未固结土的问题，提出框架预应力锚杆微型钢管桩联合支护结构，采用ADINA 有限元软件建立框架预应力锚杆微型钢管桩与土体相互作用的计算模型，与传统桩锚支护结构相比，联合支护结构可以更有效减小基坑土体位移；王海军等[10]考虑到传统框架的刚性设计，针对地震作用下框架梁易破坏失效的问题，提出“刚柔结合”的抗震思路及边坡-支护“共同承载”的思路，释放锚固支座与框架梁处的自由度，将刚性变为柔性铰接支护体系，使柔性框架锚固支护可有效控制地震影响下的边坡滑动并改善内力状态；朱彦鹏等[11]基于塑性力学极限分析上限理论的基本原理，推导了预应力锚杆支护边坡的安全系数计算式，采用Matlab 对推导公式进行全局最优解搜索，最后通过正交试验确定在框架预应力锚杆支护边坡中坡角为稳定性最重要影响因素；董建华等[12]针对软土含水量高、强度低所导致的锚杆承载力较低的问题，提出了石灰钉复合框架预应力锚杆支护结构，可以有效降低坡体的孔隙水压力、位移及锚杆轴力。

综上，目前大量对框架预应力锚杆支护结构的研究都着重于支护效果及锚杆构件的优化，对框架构件的设计及优化研究相对较少。如何合理优化框架构件，设计可靠且经济的框架连接形式十分必要。

本文在传统结构的基础上提出新型柔性铰接框架锚杆支护结构（图1），基于三维快速拉格朗日法，对典型土质边坡在自然状态、传统框架锚固体系、柔性铰接框架锚固体系下的状态进行求解，对比加固效果及框架构件自身状态，以期在荷载条件下改善框架本身易破坏部位的应力状态，起到有效控制边坡滑动的作用。

图1 刚性框架锚固体与柔性铰接框架锚固体示意Fig.1 Schematic diagram of rigid frame anchorage and flexible hinged frame anchorage system

1 设计原理及力学模型

1.1 柔性铰接框架锚固体系设计原理

边坡支护后由两部分组成：边坡自身和支护体系，两部分紧密结合，协同工作，共同确保边坡的稳定和安全。传统框架锚固体系的框架部位为薄弱点，在地震、暴雨等作用下，容易发生破坏失效。依据传力机制的优化、自由度的解除以及边坡能量耗散的设计原理，将锚杆支座与框架结构之间整体浇筑的刚性连接改为铰链连接，建立一种整体柔性边坡支护体系—柔性铰接框架锚固体系。具体方法为：将锚杆套入特制支座中，在混凝土框架与土体之间先铺设一层木板，增加传力面积以减小锚下结构的变形，提高锚下结构的承载能力；支座与格埂连接部位通过自由铰链连接，解除三向转动自由度，然后再挂网喷射混凝土，使混凝土喷射层与混凝土格埂有效黏结（图2）。柔性铰接框架锚固体系具有四方面优势：（1）减少了混凝土用料，降低了工程成本；（2）柔性铰接框架支护的锚固力通过支铰传递到框架，使边坡土体内部产生一定的应力调整，进而限制边坡的滑动；（3）解除锚杆的转动自由度，减小锚杆与框架接触部位的应力集中，进而避免支护本身的破坏；（4）柔性支护允许边坡整体和支护体系的适度变形，进而产生边坡能量耗散，减缓坡面破坏速度，增强边坡稳定性。

图2 边坡不同框架支护体系对比Fig.2 Comparison of different frame support systems for slope

1.2 计算力学模型

为了测试柔性铰接框架锚固体系的性能，采用Flac3D有限差分软件构建了相应的边坡、格构、锚杆和支铰模型，并采用强度折减法对边坡失稳和安全系数进行模拟计算和稳定性判断。本构模型采用摩尔-库伦弹塑性本构模型；锚杆采用Flac3D的cable 单元模拟；格构采用混凝土实体单元模拟。

对于柔性框架，采用Flac3D的beam 单元将锚头下混凝土垫层与实体梁相连接，释放连接部位的x、y、z向旋转自由度。在beam 模型中创建梁单元时，程序定义的梁构建坐标系统（图3）规则如下：梁结构单元共有12 个自由度，选取梁截面的中心轴作为x轴，两端梁截面的形心分别为节点1 和节点2，x轴的方向为从节点1 到节点2，与梁截面的法向方向垂直；在横截面上y轴与单元节点力矢量Y的投影对齐；z轴与梁的切线方向重合。u、w、v分别为x、y、z方向下的节点位移分量；θ为单元节点转角。根据上述规则计算每个梁单元的刚度矩阵，并将其组装成整个结构的刚度矩阵。

图3 beam 结构单元坐标系统及12 个自由度Fig.3 Beam structural unit coordinate system and 12 degrees of freedom

2 数值模型

三维数值模型高21 m，宽12 m，长35 m，护坡高14 m，水平宽14 m，坡长20 m，坡度为45°。模型的构建遵循“点→线→面→体”自下而上的建模技术，网格剖分见图4，采用空间六面体单元和五面体单元相结合的剖分方式。模型材料主要分为土质边坡与混凝土格埂，锚杆采用φ22 预应力锚杆。材料参数见表1。

表1 材料物理力学参数Tab.1 Physical and mechanical parameters of materials

图4 边坡数值模型Fig.4 Numerical model for slope

采用刚性连接框架支护体系加固的土质边坡模型上覆盖混凝土框架结构，框架沿宽度方向布置2 格，沿高度方向布置4 格。混凝土框架高0.6 m，其中1/3 埋入土体内，框架间距为4 m。每一框架交接点处打入锚杆，上面3 排锚杆长度为14 m，最下1 排锚杆为10 m，锚杆末端被固定于土体中，使其具备良好锚固力。具体布置见图5。

图5 刚性连接框架支护模型Fig.5 Rigid connection frame support model

与刚性连接框架支护体系相似，柔性铰接框架支护的边坡模型上覆盖混凝土框架结构，框架沿宽度方向布置2 格，沿高度方向布置4 格。混凝土框架高0.6 m，其中0.2 m 埋入土体内，框架间距为4 m，每一框架交接点处打入锚杆，上面3 排长14 m，最下部1 排长10 m。混凝土框架与土体之间的接触模型将框架交接点周围混凝土刚性结构去除，改为由Flac3D中梁单元模拟柔性连接。通过合理变化，增加锚杆与梁之间自由度，使体系变为柔性框架连接预应力锚杆支护。具体布置见图6。

图6 柔性铰接框架支护模型Fig.6 Flexible hinged frame support model

3 结果及讨论

3.1 边坡坡面变形

参考《建筑边坡工程技术规范》[13]《煤炭工业露天矿边坡工程监测规范》[14]及文献[15]中对边坡土体侧向变形的允许值进行稳定性评价，允许极限变形值取护坡坡长L的0.75%，即150 mm。对边坡土体物理参数进行折减，随着折减系数不断增大，边坡土体的初始位移逐渐增大。对于未经支护的天然土体边坡，当折减系数为1.8 时，4 个监测点平均位移为14 mm，当折减系数为2.0 时，各监测点平均位移为41 mm，当折减系数增大至2.2 时，护坡土体侧向位移迅速增大，各监测点平均位移达到219 mm。根据边坡稳定理论，认为折减系数取2.2 时，边坡已经发生滑动破坏。采用刚性框架支护加固后，随着折减系数增大，边坡侧向变形值明显减小。当折减系数增至2.2 时，各监测点的平均位移在117 mm 左右，此时边坡相对稳定。当折减系数增至2.4 时，边坡位移迅速增大，各监测点平均位移达到344 mm，远远超过了允许极限变形值150 mm。因此认为折减系数取2.4 时，边坡发生滑动破坏。采用柔性框架预应力锚杆对边坡进行加固后，当折减系数增至2.4 时，测点1 位移为128.5 mm，测点2 位移为139.6 mm，测点3 位移为129.8 mm，测点4 位移为140.7 mm，均未超过允许极限变形值，且较天然土体状态和刚性框架支护下有明显减小，与天然土体相比平均初始位移降低了76.0%，与刚性框架支护相比平均初始位移降低了60.8%。当折减系数增至2.6 时，边坡的稳定计算仍然能收敛，并且土体仍能达到平衡状态。由此可见，柔性框架预应力锚杆体系能很好地抑制边坡表面滑动，具备良好加固效果（图7）。

图7 各监测点初始位移Fig.7 Initial displacement of each monitoring point

3.2 边坡潜在滑动面

由Mohr-Coulomb 理论可知，剪应力是岩土体破坏的重要因素之一。因此，边坡潜在滑动面可通过分析边坡土体的剪应变增量来确定。

将剪应变增量突变和明显滑移面作为边坡失稳判据。当折减系数为1.6、1.8、2.0 时，刚性框架支护最大剪应变增量分别为2.28×10-3、9.46×10-3、3.37×10-2。当折减系数增大到2.2 时，刚性框架支护的塑性应变从坡脚到坡顶贯通，出现了明显滑移面（见图8（a））。经过柔性框架预应力支护加固后的边坡，剪应变增量明显减小。当折减系数增至 2.2 时，柔性框架支护最大剪应变增量为 2.30×10-2，且未出现明显潜在滑动面，加固效果良好（见图8（b））。

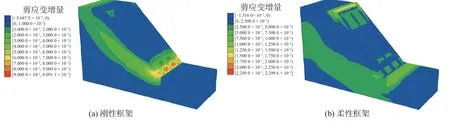
图8 刚性框架和柔性框架支护折减系数（2.2）下边坡剪应变增量Fig.8 Shear strain increment of slope with rigid and flexible hinged frame support under reduction coefficient of 2.2

天然土体、传统刚性框架和柔性框架支护状态下，计算位移和剪应变增量的对比如图9 所示。结果显示，柔性框架相较于天然土体和传统刚性框架支护状态下，随着折减系数增大，剪应变增量和位移增长速率明显降低。折减系数为 2.0 时，天然土体护坡剪应变增量突变，天然土体边坡失稳；折减系数为 2.2 时，刚性框架支护的边坡失稳；折减系数为 2.4 时，柔性框架支护边坡仍可提供有效支撑。因此，柔性框架支护在抑制边坡表面滑动方面的锚固效果更为突出。

图9 边坡位移和剪应变对比Fig.9 Comparison of slope displacement and shear strain under different supports

3.3 框架应力分析

混凝土框架与预应力锚杆为一个整体，混凝土框架是否稳定对边坡稳定至关重要。下面分析两种连接形式框架各横梁、立柱的受力。对框架上各个监测横梁与立柱进行编号（图10），横梁从坡底向上编号依次为①、②、③、④，立柱从坡底向上依次为⑤、⑥、⑦、⑧。

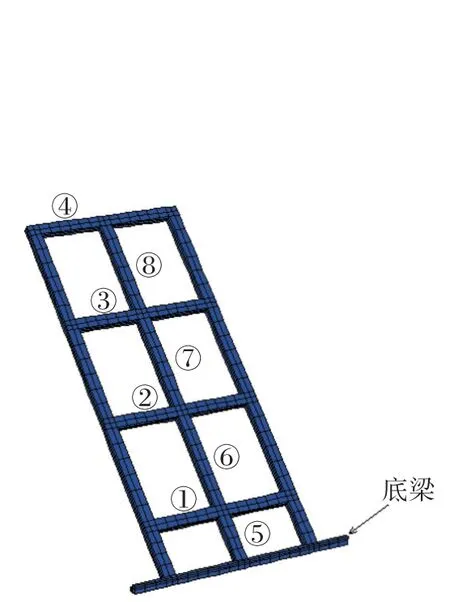
图10 框架监测位置Fig.10 Frame monitoring position

折减系数为 2.1 时，刚性框架与柔性框架最大拉应力见图11。分析框架8 个监测位置的计算结果可见，边坡发生滑动破坏时，刚性框架拉应力主要集中在框架坡顶的横梁、立柱及靠近坡顶框架节点处，为拉裂破坏的主要位置。而柔性框架横梁部位的拉应力分布较为均匀，最大拉应力约为0.85 MPa；柔性框架立柱的最大拉应力随着边坡高度增加而增大，⑧#立柱>⑦#立柱>⑥#立柱>⑤#立柱。柔性框架结构相比刚性框架结构明显降低了横梁和立柱的拉应力，相同位置处柔性框架最大拉应力仅为刚性框架的70%左右。对于刚性框架而言，靠近坡顶的③#横梁、④#横梁和⑧#立柱相较其他监测位置拉应力最大，均在1.00 MPa 以上，接近C25 混凝土的抗拉强度标准值，发生拉裂破坏的可能性最大。柔性框架支护体系对以上3 个部位拉应力改善较为明显，柔性框架结构①#横梁最大拉应力降低至0.76 MPa，②#横梁最大拉应力降低至0.87 MPa，⑧#立柱最大拉应力降低至0.74 MPa，最大拉应力平均约降低30%，混凝土框架的耐久性得到提升。分析其他横梁与立柱结果可得到相同结论（图12）。

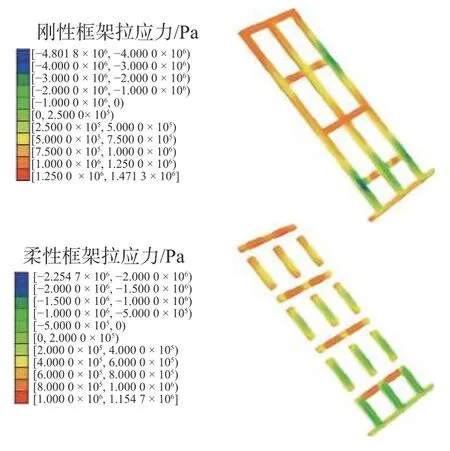
图11 框架最大拉应力（折减系数2.1）对比Fig.11 Comparison of maximum tensile stress of frame (reduction coefficient 2.1)

图12 监测横梁与立柱最大拉应力对比Fig.12 Comparison of maximum tensile stress between crossbeam and upright column at monitoring point

折减系数为2.1 时，刚性框架与柔性框架最大压应力见图13。通过计算可知，柔性框架结构最大压应力明显小于刚性框架结构。框架中靠近坡脚的横梁与立柱压应力较大，①#梁最大压应力为1.80 MPa，⑤#立柱最大压应力为1.48 MPa；柔性框架结构①#梁最大压应力降低至0.79 MPa，⑤#立柱最大压应力降低至0.82 MPa。结果显示，柔性框架结构同样可以降低框架各横梁立柱的压应力，并且改善效果明显。分析各监测衡量与立柱最大主压应力结果可得到相同结论（图14）。

图13 框架最大压应力（折减系数2.1）对比Fig.13 Comparison of maximum compressive stress of frame(reduction coefficient 2.1)

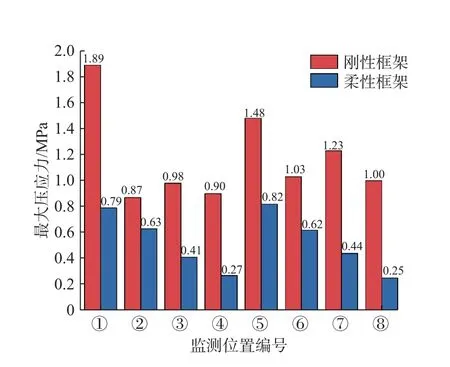
图14 监测横梁与立柱最大压应力对比Fig.14 Comparison of maximum compressive stress between crossbeam and upright column at monitoring point

4 结语

通过对传统框架锚固体系的支座连接部位设置铰接的方式，建立了铰接框架锚固新体系。传统框架体系的锚固力通过框架结构直接作用于边坡表面，柔性铰接框架支护的锚固力通过支铰传递到框架，进而通过框架限制整个边坡面的位移、滑动来进行边坡支护。在应力、弯矩较为集中且容易破坏的部位设置柔性铰，解除转动自由度以减小应力集中，进而避免支护本身的破坏。柔性支护允许边坡整体和支护体系的适度变形，利于边坡能量的耗散，起到边坡支护的效果。

采用强度折减法对边坡失稳与安全系数模拟结果表明：支护与边坡为一个整体，支护稳定对边坡稳定至关重要。通过边坡坡面变形和剪应变增量计算，折减系数为2.0 时，天然土体边坡滑动失稳；折减系数为2.2 时，刚性框架支护出现明显滑移面；折减系数为2.4 时，柔性框架支护边坡未出现较大变形和明显滑动面，仍可提供有效支撑。新型柔性铰接框架支护体系对边坡加固效果良好，可控制其滑动和剪应变增量发展。柔性支护相比于刚性支护对横梁的受力有较大改善，能够明显降低横梁和立柱的拉应力与压应力。相较于刚性支护，柔性支护最大主拉应力整体降低29%，最大主压应力整体降低55%，抗拉和抗压效果提升明显。柔性支护设计中可以降低横梁和立柱的设计标准。边坡发生滑移时，靠近边坡底部的横梁与纵梁的受力较大，设计时应考虑加固措施。