泵站建筑物变形面板数据聚类分析方法

娄本星 ，祁 洁，马福恒，周晨露

(1.南京水利科学研究院，江苏 南京 210029；2.河海大学 水利水电学院，江苏 南京 210098；3.南水北调东线江苏水源有限责任公司，江苏 南京 210009)

泵站建筑物是常见的水工建筑物之一，在供水、防洪、排涝、灌溉等方面具有重要作用。目前，泵站建筑物监测系统日益完善，定期测量以获取建筑物的状态信息，其监测信息包含有时间和截面（空间）两种属性，可以作为一种面板数据。传统的泵站监测方法以单测点一维监测序列为主[1]，难以反映泵站不同区域的实际运行状态。虽然泵站各监测点空间位置不同，但相邻的测点间会存在一定的关联性，在相邻测点集合中分析泵站监测信息的时空变化特征，能够考虑测点间的关联性和异质性，避免由于单一测点监测信息造成的误差。

基于面板数据聚类可以挖掘出数据资源的一些潜在特征，将变化特征相似、对荷载具有同质响应的测点划分至同一类别中，进而可将传统的点分析方法发展为区域分析方法。近年来，由于单测点监测序列不能反映大坝的整体变形性态，面板数据聚类分析在大坝安全监控领域得到了应用。陈悦等[2]基于Kohonen 算法实现了混凝土坝变形分区；Shao 等[3-5]提出利用绝对距离、增量距离、增速距离来度量变形序列之间的相似性，进而利用层次聚类方法对拱坝变形区域进行划分；黄潇霏[6]基于兰氏距离和模糊C 均值算法对混凝土坝水平位移测点进行了动态聚类分区。在聚类分区方法的基础上，混凝土坝健康诊断[7]、分区监控[8]、风险分析[9]、缺失值处理[10]等方面也得到了进一步发展。目前，分区监测模型在大坝安全监控领域得到了广泛应用，但在泵站建筑物安全监测中的应用较少。在南水北调东线工程中，泵站建筑物监测点众多，仅采用单一测点信息难以实现对泵站整体运行状态的把握与评估，有必要对泵站建筑物变形测点进行聚类分区。此外，时间序列相似度指标及度量方法是面板数据挖掘和划分的重要依据[11]，学者们针对各自领域提出了不同的相似度指标度量方法，包括欧氏距离[12]、相关系数[13]、变化趋势[14-15]、动态时间规整（DTW）[16-18]等。但在这些方法中，不同相似度指标反映的数据序列特征侧重点不同，因此构建适用于泵站面板数据的相似度指标是本文的研究重点之一。

鉴于此，本文以泵站垂直位移为研究对象，考虑泵站建筑物面板数据特点，基于DTW 算法构建融合趋势信息与点对点距离的相似度指标及度量方法，提出相应的综合距离指标；引入空间关联矩阵以修正邻近矩阵，建立考虑测点空间位置的改进Ward 层次聚类方法；最后结合南水北调工程某泵站枢纽，验证所构建的面板数据聚类模型的有效性。

1 泵站面板数据相似度指标及度量方法

1.1 数据标准化处理

在衡量序列间的相似度之前，为了减小量纲和数据范围的影响，首先要对监测序列进行标准化处理，使各个变量处在同一量级。假设泵站监测点数目为N，监测时间截面数目为T，其面板数据可以表示为：

本文采用Z-score 方法对泵站监测数据进行标准化，则任意一点变形值xij标准化如式（2）所示：

经过标准化处理后的面板数据平均值为0，标准差为1。大部分数据分布在[-1,1]之间，限制了数据的取值范围，可以消除量级和奇异值的影响。

1.2 动态时间规整

泵站结构中通常会设置分缝，分缝会导致各部分的变形敏感性差异，即各测点监测序列在时间尺度上可能存在相位差，若直接用欧氏距离来度量监测序列之间的相似度，很有可能与直观判断结果不符，得出的相似度偏大。为此，采用DTW 算法来衡量监测序列的相似性，DTW 算法通过在两个序列间进行非线性映射（图1），对时间轴重新规整，以搜索出两组序列间的最优对应关系和最小距离，能够有效解决监测序列间存在的相位偏移问题。

图1 DTW 算法点对点映射图Fig.1 Mapping diagram of DTW algorithm

假设有2 个测点的监测序列X和Y，分别表示为X={x1,x2,x3,···,xm}，Y={y1,y2,y3,···,yn}，m和n分别是X和Y的时间截面长度。然后构造一个m×n的矩阵d，矩阵元素d(i,j) 表示xi与yj之间的距离，定义距离函数为f(xi,yj)，则有：

DTW 算法的整体思路是通过非线性映射规整2 个序列，找出最优路径使得路径上的距离最小[18]。通过DTW 算法重新规整的最优路径 Φ，定义为：

式中：Φx(k)和 Φy(k) 分别为映射后监测序列X和Y的索引值；p表示规整后最佳路径 Φ的长度，且满足max(m,n) ≤p≤m+n。则原监测序列X和Y可以规整为长度均为p的监测序列表示为：

原监测序列X和Y之间的距离可以用规整后监测序列X和Y之间的距离来衡量，因此，对于任意监测序列X和Y，其点对点距离或相似度d1为:

1.3 DTW 改进方法

对于大多数的监测序列，DTW 算法可以很好地解决序列之间的相位偏移问题，但不能考虑监测序列的趋势性变化。在泵站建筑物监测序列中，通常会遇到以下两种情况：

（1）如图2 所示，序列1 和2 属于同一类型，变化趋势相似，但点对点距离比较大；序列1 和3 属于不同类型，变化趋势差异极大，但点对点距离较小；此时单独采用DTW 算法会导致分类错误，会将序列1 和3 划为同一类，这显然不符合实际情况。

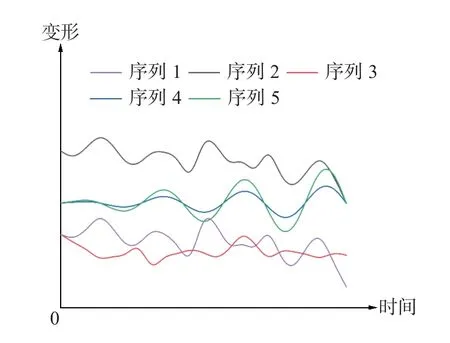
图2 DTW 算法存在的缺陷Fig.2 Defects of DTW algorithm

图3 序列趋势转换Fig.3 The method of trend conversion

（2）如图2 所示，序列4 和5 属于同一类型，变化趋势相同但数据波动幅度不同，此时单独采用DTW 算法得到的距离偏大，易产生误判。

产生上述结果的原因是DTW 算法不能兼顾序列的变化趋势，为了避免此种分类错误的产生，充分考虑监测序列的变化趋势信息，本文提出一种监测序列变化趋势提取方法和相似度度量方法。

根据以上规则来提取和表示监测序列的趋势信息，具有以下两个优点：

（1）转化后的序列值只与序列的变化趋势相关，与序列的震荡幅度无关，即对振幅不敏感。这样可以避免由于数据振幅变化差距过大带来的分类误差，有效度量监测序列之间的相似性。

（2）经Z-score 方法标准化处理后大部分的数据在[-1,1]范围内，选用{-1，0，1}分别表示监测序列的下降、不变、上升等趋势信息，与标准化处理后的序列量级相一致，为融合趋势信息和点对点距离奠定了基础。

因此，对于任意监测序列X和Y，首先采用DTW算法后规整为X和Y，再将其转化趋势信息z(X)和z(Y)，则基于趋势信息的相似度指标d2表示为：

1.4 综合相似度（距离）

为了提高聚类分析的准确率，综合考虑序列的变化趋势信息和点对点之间的距离，定义任意两序列间的综合相似度或距离D为：

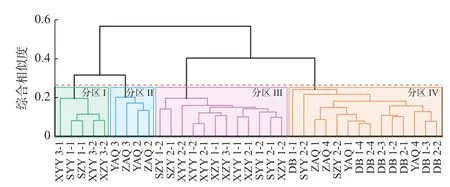
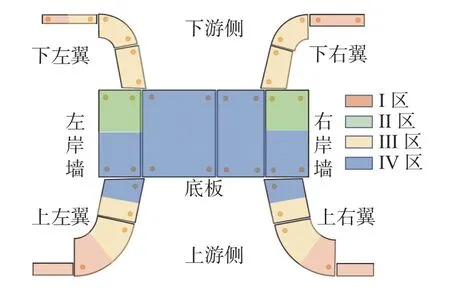
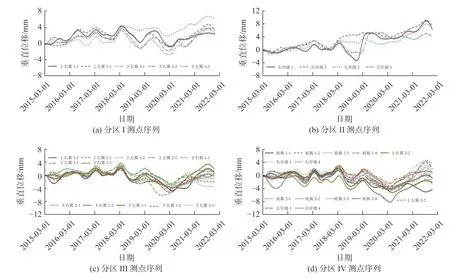
式中：w1和w2分别为d1和d2的权重系数，且w1+w2=1。当w1=1、w2=0 时，此时综合距离为D(X,Y)=d1(X,Y)；当 0

2 泵站面板数据聚类分析方法

2.1 层次聚类方法

聚类分析中常用的两种算法是划分聚类和层次聚类。划分聚类需要给定簇数，但对泵站面板数据进行聚类分析时，不能预知聚类的数目，因此本文选取Ward 层次聚类方法。该方法将每个样本看作一类，然后根据邻近矩阵D中的相似度（由式（9）计算得出）对不同类进行聚合，在合并过程中使组内离差平方和最小，最终逐级依次合并所有类别。假设泵站共有N个测点被划分为k个类别，分别记为G1、G2、···、Gk，每个类别中测点个数记为N1、N2、···、Nk，则k个类别的总离差平方和[10]为：

确定类的数目是层次聚类分析中的重要内容，可以设置适当的阈值作为划分依据。当聚类数目从n-1 到n时，增加的组间离差平方和记为 ∆wn；当聚类数目从n到n+1 时，增加的组间离差平方和记为∆wn+1；若满足∆wn>>∆wn+1，则认为最佳聚类数目为n。

2.2 考虑泵站空间关联性的聚类分析方法

泵站建筑物由进水建筑物、泵房、出水建筑物等组成，典型的泵站布置如图4 所示。可以看出，泵站结构布置形式基本对称但形状却不规则，直接采用以上方法进行聚类分析仅能考虑监测序列的相似性，不能考虑到测点空间位置的连续性，会出现分区不连续的情况。为了在聚类分析中考虑空间的连续性，将底板和岸墙处测点集合记为A；上下游翼墙处测点集合记为B={B1，B2，B3，B4}，分别对应4 个翼墙；将集合A与B相邻的点集记为，分别对应翼墙与泵房的邻接的4 个部分（图4C={C1，C2，C3，C4}中的红色圆圈中的测点）。定义连续性条件为：如果集合A和Bi中的测点被划为同一分区，则需要经过集合Ci中的测点作为媒介连接。为此，引入空间关联矩阵Z来修正层次聚类中的邻近矩阵D，以解决上述聚类分析中的空间合理性问题。改进方法具体如下：

图4 泵站建筑物结构布置Fig.4 Structure layout of pump station buildings

（1）首先建立N×N的空间关联矩阵Z和邻近矩阵D，令Zij=1，Dij=d(Xi,Xj)。

（3）在聚类完成后，分为以下两种情况：

①∀i∈A,j∈Bn，且i,j∉G，则直接转至步骤（5）；

②∃i∈A,j∈Bn，且i,j∈G。若存在i,j∈Cn且 分区G在空间上连续，则转至步骤（5）；若i,j∉Cn或分区G不连续，则令Zij=Zij+∆k，i、j表示测点序号，Δk为迭代步长，可根据实际聚类过程调整。

（4）重复迭代步骤（2）和（3），直到满足连续性条件。

（5）得到最终的聚类结果。

3 工程应用

根据上述所提出的泵站面板数据聚类分区方法，以南水北调东线工程某泵站枢纽垂直位移测点为例，验证模型的有效性。该泵站垂直位移观测标点共有36 个，测点布设见图5。研究对象为该泵站36 个测点从2015 年3 月30 日—2021 年12 月15 日的垂直位移监测数据。（注：泵站下左翼2-2 测点数据缺失）

图5 垂直位移测点布置Fig.5 Layout of vertical displacement monitoring points

基于泵站面板数据聚类分区方法，对泵站的36 个测点监测序列进行聚类分区得到聚类谱系图（图6）。根据组间离差平方和增加的幅度，最终将泵站测点划分为4 个区域（Ⅰ区、Ⅱ区、Ⅲ区、Ⅳ区）。将图6 中的计算结果绘制于泵站测点分布图上（测点命名规则为测点部位首字母缩写+序号，如XYY3-1 表示下右翼3-1），各分区结果在空间上的位置如图7 所示（下左翼2-2 测点根据相邻测点的结果被划为分区Ⅲ）。从聚类结果的分布图可以看出，变形分区结果在空间上沿着水流方向左右侧高度对称。

图6 泵站垂直位移测点聚类图Fig.6 Clustering results of vertical displacement for pump station

图7 泵站垂位移测点聚类分区结果Fig.7 Zoning results of vertical displacement for pump station

如图6 所示，从谱系图顶点出发，首先可以将所有测点分为两大类：（1）分区Ⅰ和分区Ⅱ，包括泵站翼墙边缘与岸墙部分测点；（2）分区Ⅲ和分区Ⅳ，包括泵站底板、靠近底板的翼墙及岸墙部分测点。

图8 给出了各分区测点的监测序列（正为下沉，负为上升）。从测点序列发展趋势上来看，第（Ⅰ）大类与第（Ⅱ）大类测点的发展趋势明显不同，第（Ⅰ）大类测点序列整体呈增加趋势，即测点下沉；第（Ⅱ）大类测点序列整体呈减小趋势，即测点上升；沿着谱系图继续向下发展，这两大类测点根据空间分布、发展趋势、波动幅度的差异可分别分为分区Ⅰ和分区Ⅱ、分区Ⅲ和分区Ⅳ。

图8 各分区测点监测序列Fig.8 Monitoring sequence of measuring points in four zones

结合泵站建筑物的设计资料，从运行期的荷载特点来看，各分区的受荷特点也有明显的不同。

分区Ⅰ：泵站上下游侧第3 节翼墙挡土高度较小，结构形式为钢筋混凝土悬臂式结构；其底板高程比第2 节翼墙底板高程高出较多，略低于运行期上下游水位，受上下游水荷载的影响较小，主要受土压力与地基固结沉降的影响，因此呈轻微下沉趋势。

分区Ⅱ：泵站左右岸墙的上下游侧工作平台高程存在显著差异，其上游侧工作平台高程为12.1 m，下游侧工作平台高程为9.5 m。上下游不均匀的土压力导致左右岸墙有倾向下游侧的发展趋势，因此，左右岸墙上游侧测点主要呈上升趋势，下游侧测点主要呈下沉趋势。

分区Ⅲ和分区Ⅳ：泵站站身和上下游第1、2 节翼墙的底板高程范围为-5.3～-1.0 m，而运行期上游水位范围为7.41～10.68 m，下游水位范围为5.77～7.21 m，因此该分区内测点垂直位移受上下游水位带来的浮托力影响较大，主要呈轻微上升的趋势。

综合以上分析，验证了本文所提出的泵站面板数据聚类分区方法是比较合理的，能够挖掘出泵站面板数据中的一些潜在信息，有效反映出泵站各区域的变形特征和荷载特点，可为泵站安全监控的分区域管理提供理论依据。

4 结语

基于面板数据聚类理论和DTW 算法，提出了基于趋势信息和点对点距离的融合相似度指标及度量方法；基于Ward 层次聚类法，构建了考虑空间关联性的泵站测点聚类方法，进而建立了泵站面板数据的聚类分区模型。最后结合某泵站枢纽垂直位移实测数据，验证了该模型的有效性。

本文所建立的泵站面板数据相似度指标比较合理，能够综合反映监测序列的变化特征；改进后的层次聚类方法能够兼顾泵站结构布置特点和测点的空间关联性，保证了聚类分区的连续性。工程实例分析表明，泵站面板数据分区结果在空间上沿着水流方向高度对称，能够有效反映出泵站各区域的变形特征和荷载特点，可为进一步建立泵站变形分区监控模型提供理论依据。