基于声回波特性的引水隧洞表面声点云去噪

王吉松 ，张学武，徐晓龙，宋 轲

(1.河海大学 物联网工程学院，江苏 常州 213022；2.淮阴师范学院 计算机科学与技术学院，江苏 淮安 223300)

引水隧洞由于复杂的运行环境，经长年运行后内表面可能出现裂缝、剥落、隆起等损伤，若不能及时发现并处理，可能会引起安全事故[1-4]。近年来，针对水下结构物表面损伤检测，提出诸多基于光学成像探测模式的方法和技术。然而，引水隧洞内部水体浑浊，存在严重散射与吸收等现象，致使光学成像探测技术在长距离、大直径充水隧洞巡检过程中无法得到期望的检测结果。声波是水下信息远距离传输的有效载体，通过采集声反射回波信号形成的声学点云，可有效反映反射物体本身特性，是当前海洋及水下目标检测的主流手段[5-8]。然而，受探测环境、探测系统及探测载体装备自身的噪声因素影响，基于声波反射机制的探测方法在隧洞内表面损伤检测过程中极易遭受噪声干扰。因此，通过研究引水隧洞内表面声点云去噪方法以降低噪声干扰、提高损伤检出率，具有重要的实际意义。

目前，有关声点云的去噪方法研究有限，主要是将激光点云滤波方法直接应用于水下声学点云中，效果甚微且具有一定的应用场景限制。冯东恒等[9]提出一种考虑水下地形特点的多波束点云去噪算法，算法基于RANSAC 思想，结合统计分析方法滤除明显离群噪声，并结合共面法矢量特征预判去除近地表噪声。然而，在存在多径回波情况下，去噪效果较差，不适合狭窄封闭的隧洞环境。解全波等[10]利用声点云强度与高程信息对水下点云进行滤波，根据原始点云的强度信息进行粗分类，并利用种子点与周围点云数据的强度信息与高程信息实现准确分类和滤波，但其滤波精度完全取决于种子点的准确性，不适用于分布不均匀且存在大量多径噪声的隧洞声点云；崔晓冬等[11]研究多波束水声点云的组合滤波算法，将噪声分为大尺度与小尺度噪声，分别采用半径滤波与双边滤波实现点云的平滑，但是存在复杂地形的误删问题。关于激光点云的去噪方法研究，主要分为基于统计思想、邻域思想及体素网格的滤波算法。基于邻域思想滤波方法利用点与其邻域点的相似性进行噪声点滤除[12-13]，其代表性算法为半径滤波算法，该方法对离群点滤除效果显著，滤波效果取决于半径和半径范围内点的数量。基于统计思想点云滤波算法假设点云某特征符合一种确定模型，而偏离模型的点云被当作噪声处理[14-15]，如果先验模型不准确，滤波结果将会有很大误差。其代表性算法为统计滤波，该方法对空间噪声点和离群面滤波效果显著，滤波效果取决于邻域点数量和标准偏差系数。基于体素的滤波方法将点云划分为多个三维网格，使用相关方法选择网格中的一点近似代替网格中所有点[16-17]，该方法能实现点云的下采样，但经常会导致点云局部特征的丢失，且网格的划分直接影响滤波效果。

基于声波反射机制的隧洞内表面病害探测原理为：探测设备采集反射回波信号形成声回波点云图，通过点云图对隧洞内表面进行损伤探测与识别。所得声回波数据点云具有稀疏性特点，其内每一点均包含回波强度属性信息及点几何位置信息。隧洞内表面不同材质及结构病害对声波呈现出不同反射特性，因此通过声回波强度属性信息可粗略反演隧洞内表面形态；声点云模型中点的几何位置信息由声呐波束开角信息、声呐设备数据采样周期、水介质中声波传播速度及水下机器人载体位置信息共同决定，表示声呐波束脚印照射的隧洞实际区域位置；通过声呐波束开角将隧洞截面的360°全向反射回波划分为顺序多帧回波数据点，随着水下机器人载体的不断行进，将隧洞不同截面回波数据点进行拼接从而形成隧洞内表面声回波点云，因此，隧洞截面内相邻数据帧之间及相邻断面数据之间在空间位置上均具有连续性。然而，声点云虽是隧洞内表面回波数据，但由于声波具有固有的宽度特性，对声回波进行采样会形成多个离散数据点，再通过拼接相邻断面数据会形成一个类似团状的立体点云，这与激光平面点云有着本质区别，以致适合激光平面点云的有效滤波方法不能直接用于团状立体声点云。

因此，本文提出一种基于声回波特性的引水隧洞内表面声点云去噪方法，该方法利用声回波固有宽度特性形成的多回波数据点及声波叠加特性形成的数据点高强度值，结合点云空间位置信息实现团状立体隧洞内表面声点云的滤波，从而为引水隧洞内表面损伤的检测提供高精度、高可靠数据支撑。

1 基于声回波特性的声点云去噪方法

基于声波反射原理采集的原始回波数据为一系列无序、离散数据点，利用载体姿态信息校正后，通过声呐扫描机制建立回波点云与隧洞空间位置映射关系，并通过拼接相邻断面数据生成隧洞内表面点云模型。如图1 所示，依据回波数据采样点的位置区域，将隧洞点云模型分为4 个区域：直达波区域、水体区域、隧洞内表面回波区域和高次回波区域。依据区域数据对探测结果的贡献度，将直达波区域与高次回波区域定义为非特征区域；将水体区域与隧洞内表面回波区域定义为特征区域。下面结合工程特点对点云模型的4 个区域进行详细阐述，并使用不同的方法对所定义的非特征区域、特征区域数据进行去噪。

图1 隧洞回波点云模型划分示意Fig.1 Schematic diagram of area division of tunnel echo point cloud model

1.1 非特征区域数据去噪

非特征区域指该区域内数据对隧洞内表面病害检测贡献可忽略不计，主要包括直达波区域和高次回波区域。直达波区域数据（图1 中黑色点）是指发射声波未经隧洞内表面反射，而在发射声波的同时直接被传感器接收的数据，由声呐传感器自身设计因素及数据的同步采样机制形成，该区域数据点并非隧洞内表面实际反射回波数据，可认为是对隧洞病害检测无贡献的数据点。因此需要通过研究声呐传感器的固有设计参数来获得直达波区域边界值，实现直达波区域数据的有效去除。本文采用的全向扫描声呐为同步采样，即发射声波的同时启动接收回波数据，故固定宽度的发射声波会被直接采样形成直达波数据点，数据点数量由发射声波宽度及采样周期确定；为保护声呐探头免受碰撞，声呐设备会加装保护罩，而全向声呐需要使用转子驱动传感器探头以实现旋转扫描，因此在保护罩与传感器探头之间存在耦合介质层；声波在耦合介质层传播期间，以及经保护罩反射的回波在耦合介质层传播期间，被周期采样形成的数据点亦属于直达波数据点。由以上分析可得，直达波区域边界阈值由声呐传感器发射声波宽度、采样周期、耦合介质层宽度、声速等参数确定，计算式如下：

式中：N为直达波区域上边界阈值；Wp为 发射声波的固有宽度（s）；d为声呐传感器耦合介质层宽度（m）；Ts为采样周期（s）；c为水中声速（m/s）；为向上取整数符号，保证回波数据点索引号为整数。N由隧洞回波数据点的索引号表示，可根据采样周期转化为距离度量，下边界阈值的数据点索引号为0。Wp通过与声呐采样周期Ts相除可得到发射声波直接被接收传感器采样所形成的直达波数据点数量。由于接收传感器采集的是经过保护罩反射的回波数据，因此声波传播距离为双倍耦合介质层宽度（2d）；通过与声速c相除可得到声波在双倍耦合介质层内的传播时间，再与采样周期Ts相除可得到声波在耦合介质层传播所形成的直达波数据点数量。将直接采样及保护罩反射所形成的直达波数据点数量相加得到最终的直达波区域数据点数量，即直达波区域上边界阈值。

除直达波区域外，隧洞内表面回波采样数据中还存在由于多径效应形成的高次回波区域（图1 中蓝色点）。多径效应是指首次回波被传感器接收后，声波再次或者多次在隧洞内壁发生反射后继续被传感器接收。高次回波区域属于冗余数据，虽能部分反映隧洞的实际形状，但是由于隧洞表面实际回波数据的存在，此部分冗余数据贡献度可忽略，因此需要找出高次回波区域的边界阈值并对此区域数据进行滤除。理论上，高次回波到达接收传感器的传播时间要晚于实际隧洞回波的传播时间，因此高次回波数据区域位置位于隧洞内表面回波数据区域位置之后。同直达波区域边界阈值分析相似，高次回波区域的边界阈值不仅取决于声呐传感器自身发射声波宽度、采样周期、耦合介质层宽度、声速等固有参数，还与隧洞的最大半径有关。由以上分析所得，高次回波区域边界阈值计算如式（2）所示：

式中：M为高次回波区域下边界阈值；rmax为隧洞最大有效半径(m)。M由隧洞回波数据点的索引号表示，可根据采样周期转化为距离度量，上边界阈值为声呐最大回波采样点索引号，本文取179；因为长距离隧洞会存在半径不一现象，因此判断高次回波区域边界阈值时应选择隧洞最大半径，以防去除实际有效数据。通过隧洞的最大有效半径与声速可以得到隧洞内表面反射首次回波的传播时间，再与采样周期相除可得到首次回波的采样数据点数量，与直达波区域采样数据点数量相加即可得到最终的高次回波区域下边界阈值。

通过式（1）和（2）可以计算得到直达波区域和高次回波区域的边界阈值，从而确定直达波区域、高次回波区域，直接滤除这两类区域内的回波数据点。

1.2 特征区域数据去噪

相比非特征区域数据，位于特征区域内的噪声数据（如图1 中的红色点与绿色点），尤其是水体区域内的噪声数据去噪较为复杂，因为水体区域内数据可能是水体中存在的真实障碍物的反射回波数据，若作为非特征区域噪声数据点直接进行滤除势必会影响检测结果的真实性。针对特征区域数据去噪，本文利用声回波固有宽度特性形成的多回波数据点及声波叠加特性形成的数据点高强度值，结合空间位置信息实现声点云去噪。

由于声波固有的宽度特性，反射回波信号亦具有一定宽度，其经过周期采样必定会形成多个数据点，这与噪声数据点的形成机制有本质区别，因此通过连续非零值数据点数量这一声回波特性参数可以在保留实际障碍物数据点同时滤除其他噪声数据点。另外，受到噪声的影响，采集到的非零数据点序列前端部分强度值往往较小，并不能作为隧洞内表面实际回波数据点；相反，声波的叠加特性会使隧洞内表面实际回波产生高强度值数据点。因此通过强度阈值参数可以滤除回波数据中低强度值数据点。考虑到隧洞内表面一定区域内特征的相似性，所提方法同时结合隧洞点云模型中点的空间位置信息，通过待滤波点所在的当前数据帧、相邻数据帧及相邻断面对应位置处的数据帧联合执行滤波，滤波示意见图2。

图2 特征区域数据点去噪示意Fig.2 Schematic diagram of data point denoising in characteristic area

图2 为隧洞点云模型前视二维图像中的1 个象限区域，绿色点为隧洞回波区域数据点，红色点为水体区域数据点，蓝色点为当前待滤波数据点。蓝色虚线框为滤波方法涉及的空间位置区域，实际为立体空间区域。对于当前待滤波数据点，首先判断其当前所在数据帧内的连续非零值点数量及待滤波数据点本身强度值是否高于对应阈值，若全部高于阈值则为有效数据点并保留；若待滤波数据点的连续非零值点数量低于对应阈值，则为噪声点。对于连续非零值点数量高于阈值且本身强度值低于数据点强度阈值的待滤波数据点，则需根据其相邻数据帧内对应位置处数据点的信息继续判定；若其相邻数据帧内对应位置处数据点的连续非零值点数量及其强度均高于对应阈值，则为有效数据点并保留；若其相邻数据帧内对应位置处数据点的连续非零值点数量低于对应阈值，则为噪声点。对于待滤波数据点相邻数据帧内对应位置处数据点的非零值点数量高于阈值且其强度值低于数据点强度阈值的，则需根据相邻断面内对应位置处数据点的信息继续判定，若相邻断面内对应位置处数据点的连续非零值点数量高于阈值且其强度值高于数据点强度阈值，则为有效数据点并保留；其他情形均判定为噪声点。该方法基于声回波特性中声波固有宽度参数、声波叠加特性进行联合滤波，并融合当前帧-相邻帧-相邻断面执行空间滤波，能够既保留障碍物数据点又滤除水体区域中噪声数据点。

2 试验与分析

为验证所提方法的实际去噪效果，使用单波束全向声呐在真实测试场地中对实际隧洞进行数据采集。测试场地中隧洞呈圆形，直径为80 cm，内表面为光滑人工混凝土。单波束全向声呐发射声波宽度为20 us，信号频率为2.25 MHz，采样周期为7.5 us，声呐探头旋转步进角度为0.9°，水中声速设为1 500 m/s。使用水下无人自主航行器搭载单波束全向声呐沿隧洞中轴线作业并进行回波数据采集，采集所得数据经过载体姿态数据校正后作为验证数据源。

2.1 不同敏感参数下试验结果对比

如1.2 节所述，基于声回波特性的引水隧洞内表面声点云去噪方法执行空间滤波依赖于声回波宽度参数与回波强度参数，而声回波宽度参数的敏感性分析等效于连续非零值点数量参数的敏感性分析。故本节对连续非零值点数量与回波强度值两种敏感参数取不同数值情况下的试验结果进行对比与分析。

依据采集隧洞回波信号所用声呐传感器的固有参数，理论上回波信号应被采样为连续3 个离散数据点，但是由于噪声、设备的固有误差等影响，实际采样点数量多于理论值，因此本文将连续非零值点数量阈值参数分别选取为1、2、3、4、5 进行试验结果对比。另一方面，本文依据回波数据点强度值分布情况，首先选取原始回波数据点强度平均值作为其中一个阈值参数，然后以此强度平均值为参考，将原始回波数据点分为两部分，再分别取此两部分数据点的强度平均值作为另外2 个阈值参数进行试验对比，即选取的回波强度阈值参数Vt分别为75、165 和230 mV。并使用2 个重要的误差度量指标Dm和Rh分别对滤波效果进行评价。Dm表示滤波所得点云模型内的所有点分别与标准点云模型中与其最近点距离的平均值[18]，代表隧洞点云模型的径向重建精度误差，计算方法见式（3）。Rh表示滤波所得点云模型中孔洞在整个模型中的占比，代表点云模型表面信息的缺失程度，计算方法见式（4）。

式中：K为所得点云模型中点的数量；（xi,yi,zi）为 所得点云模型中待计算数据点的三维坐标值；为标准点云模型中与（xi,yi,zi）数 据点最近的数据点三维坐标值；Nh为所得点云模型中被滤除掉的数据点数量，即孔洞点的数量；Nt为使用所提方法滤波前点云模型中数据点的数量。

两种敏感参数下的误差度量值变化见图3。从图3（a）可见，当回波强度阈值为75 mV 时，不同连续非零值点数量的孔洞占比的平均值为3.19%，低于其他两种回波强度阈值条件下的平均值（5.57%和7.66%），且随着连续非零值点数量阈值的增大，3 种回波强度阈值参数下孔洞占比均呈现增大趋势。若仅考虑孔洞占比指标参数，应该选取回波强度阈值为75 mV、连续非零值点数量阈值为1 作为本文所提方法的最优参数；然而，从图3（b）可见，当回波强度阈值为75 mV 时，不同连续非零值点数量的Dm的平均值为4.94 cm，整体高于另外两种回波强度阈值参数下的结果（4.73 和4.66 cm），即径向重建误差最高，而回波强度阈值为230 mV 时，Dm最低，为4.66 cm。因此，径向重建精度指标与孔洞占比参数指标是矛盾体，在不同的应用场景中，需要进行折中考虑。通过图3 可以看出，连续非零值点数量阈值在1～3 区间内，Rh和Dm趋势平缓，可以近似认为保持不变态势。在两类敏感参数权重对等情况下，统筹选择连续非零值点数量阈值为3、强度阈值为165 mV 作为本文所提方法最优值。通过分析得到的连续非零值点数量敏感参数最优值亦与由声呐传感器参数计算所得的理论值保持一致，进一步证明本文方法最优参数选取的合理性。

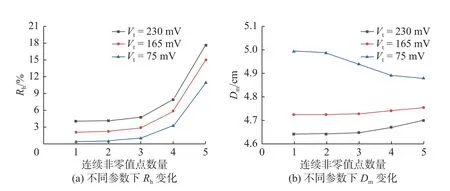
图3 不同敏感参数下误差度量值变化趋势Fig.3 Trend of evaluation index under different sensitive parameters

本文所提方法在最优参数下滤波所得的点云模型如图4 所示。相比原始点云模型，所提方法得到的点云模型在去噪和平滑效果上性能显著，处于水体区域内的噪声数据点基本被滤除，同时保留了隧洞轮廓数据点，轮廓一致性较高，并且孔洞占比小，表面特征信息丰富。由于本文所提方法是基于连续非零值点数量以及回波强度阈值参数，并且结合空间位置信息进行滤波，因此水体区域或者隧洞实际回波区域中的噪声点由于其当前所在位置的连续非零值点数量少于阈值而被滤除；类似地，若当前噪声点及其周围空间位置的数据点强度阈值不符合强度阈值参数也会被滤除，从而滤除了大量的离群点、离群面等非有效数据点，得到光滑的点云模型。如图4(a)、图4(c)所示，相比原始隧洞内表面点云模型，所得点云模型的表面平滑性得到了显著提升，隧洞轮廓周围的离群点得到了有效平滑。因此，本文所提去噪方法可获得高精度隧洞点云数据模型，从而为隧洞内表面损伤的检测与识别提供可靠数据支撑。

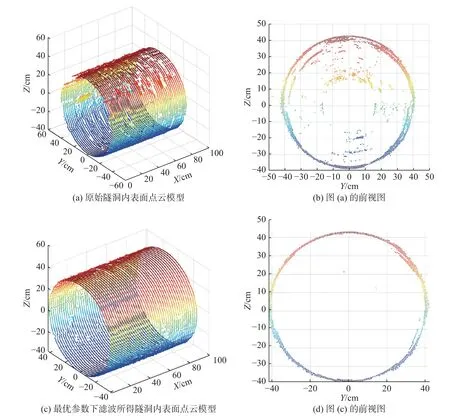
图4 最优参数下所得点云模型图与隧洞原始点云模型图Fig.4 The resultant point cloud model diagram and the original point cloud model diagram of the tunnel

2.2 与经典滤波算法试验结果对比

统计滤波与半径滤波是地面激光点云去噪的经典算法，该类算法均是通过删除点的形式实现滤波目的，与本文所提方法滤波形式一致，因此本节将所提去噪算法与上述两种经典滤波算法进行对比。半径滤波与统计滤波方法的滤波效果分别由邻域半径、半径范围内点的数量及标准差乘数阈值决定，为使算法所得结果具有可比性，将上述参数换算为最优参数，与所提算法选择的一致。

由图5 可见，半径滤波与统计滤波方法的去噪效果较差，水体区域中残留大量噪声点，导致形成的点云模型精度较差。且所得点云模型表面光滑效果差，隧洞内表面轮廓较为模糊，表面周围存在大量的噪声数据点，严重影响隧洞内表面损伤的探测与识别。本文所提方法得到的隧洞点云模型比其他两种方法的光滑性更好，对离群点的滤波效果明显，而且水体区域中的噪声数据点基本被滤除，模型轮廓精确，孔洞少。

图5 不同滤波算法所得结果对比Fig.5 Comparison of results obtained by different filtering algorithms

为定量评价去噪效果，本文使用Dm、MRMS、σ及Rh等 4 个误差度量指标。MRMS表示去噪后所得点云与标准点云模型配准后的距离均方根误差；σ表示所得点云模型与标准模型各点之间欧式距离的标准差。误差度量值计算结果见表1，最优的误差度量结果使用加粗字体表示。半径滤波方法所得结果的误差度量值最高，意味着其去噪效果最差，通过图5(a)与图5(b)可以看出，所得点云模型表面存在大量噪声数据点，且水体区域内残留大量噪声数据。统计滤波方法所得点云模型的误差度量值虽然均好于半径滤波方法，但是从图5(c)和图5(d)可以看到水体区域中依然存在大量的数据噪声点。因此，半径滤波方法与统计滤波方法所得点云模型的重建精度效果较差。相反，本文所提方法在误差度量指标上均好于其他两种方法，Dm度量值较半径滤波与统计滤波方法提高近1 cm；且标准差 σ较小，反映所提方法滤波后所得点云模型在隧洞内表面周围的聚集性较好；孔洞占比为2.81%，优于其他两种方法，表明去噪后所得点云模型的完整性较好，保留细节特征较为完整。相比于其他两种滤波方法，本文所提方法的光滑和去噪效果均具有优越性，可为隧洞内表面损伤的探测与识别提供高精度的可靠数据。

表1 不同滤波算法误差评价指标值Tab.1 Error metrics of different filtering algorithms

3 结语

引调水隧洞内表面损伤是威胁其安全运行，引起重大事故的主要隐患。定期对引调水隧洞内表面损伤进行检测，是保障其安全运行、健康管理的重要措施，也是我国防灾减灾体系的重要内容。针对基于声波反射机理的隧洞内表面损伤探测过程易遭受水体环境噪声、多径噪声及检测设备自身噪声干扰问题，本文利用声回波固有宽度特性形成的多回波数据点及声波叠加特性形成的数据点高强度值，并结合点云空间位置信息实现团状立体隧洞内表面声点云的噪声滤波以降低噪声干扰。针对本文提出的去噪方法，通过一系列试验得出以下结论：

（1）同一连续非零值点数量阈值参数下，回波强度阈值参数越小，孔洞占比越低，但是隧洞回波声点云模型径向重建误差越大；回波强度阈值参数越大，所得点云模型径向重建精度越高，但是孔洞占比也对应升高。

（2）同一回波强度阈值参数下，连续非零值点数量阈值越小，孔洞占比越低，但是隧洞模型径向重建误差越大；连续非零值点数量阈值越大，隧洞模型径向重建精度越高，但是孔洞占比也对应升高。

（3）通过与其他经典地面点云滤波算法结果对比，本文所提方法在点云模型表面的平滑性和水体区域内噪声数据的去噪效果上均优于经典算法。

本文所提方法得到的隧洞内表面点云模型表面仍然存在少许孔洞，会影响隧洞内表面损伤的检测与识别。因此，下一步将研究隧洞内表面声点云孔洞修复方法，为隧洞内表面损伤全面监测与维护提供可靠的数据支撑。