考虑长径比及冲刷的单桩基础侧向承载特性分析

张融圣，刘寒秋，朱嵘华, ，田振亚，孙 香

(1.浙江大学 海洋学院，浙江 舟山 316021；2.阳江海上风电实验室，广东 阳江 529500)

基础冲刷是导致海工结构物破坏的主要原因之一[1-2]。海上风电支撑结构基础大多采用单桩型式，冲刷会掏蚀桩基附近土体，削弱地基承载力[3]，最终影响机组的正常运行甚至导致支撑结构发生整体失稳倾覆。因此，开展冲刷作用下海上风电单桩基础的分析方法及响应变化预测研究具有重要意义。工程实践中，一般采用国内外规范[4-5]普遍推荐使用的p-y曲线法（以下简称为API 方法）来模拟海上风电桩基础的侧向桩土相互作用。但规范中并未给出考虑冲刷坑几何形态的水平受荷桩计算方法，故工程设计中常将局部冲刷直接简化为整体冲刷，造成桩基设计偏于保守[6]。针对上述问题，国内外学者普遍基于三维数值仿真及物理模型试验等研究手段开展了受局部冲刷单桩的研究。漆文刚等[7-8]基于ABAQUS 建立大直径单桩基础有限元计算模型，探讨了局部冲刷对水平承载桩基的桩土相互作用机理的影响；Qi 等[9-11]通过离心机试验，分析了整体冲刷和局部冲刷对砂土地基中的桩基水平承载力和p-y曲线的影响；Liang 等[12-13]通过理论公式推导，研究了黏性土中由于桩周土体冲刷而导致的地基土应力历史变化对桩基水平承载力的影响，提出了相应的p-y曲线修正模型。

桩基入土段长度与外径之比（L/D）是控制桩基水平承载特性的关键参数[14]，海上风电单桩基础大多属于大直径短桩，L/D通常小于10。根据小直径柔性长桩（L/D相对较大）现场试验[15-16]提出的API 方法由于忽略了由桩基长径比减小而产生的尺寸效应，往往低估了单桩基础的承载力[17-18]。海床冲刷会导致桩基入土段长径比进一步减小，使得尺寸效应对小长径比单桩基础的影响愈发突出，API 方法可能难以适用。然而，现有针对受冲刷桩基分析方面的研究，大多忽略了由冲刷引起的入土段长径比减小而带来的侧向承载特性变化，较少针对长径比对局部冲刷后桩基剩余承载力的影响开展定量分析。

本文建立考虑局部冲刷坑形态的海上风电桩基础三维有限元模型，对比不同长径比桩基受冲刷后的侧向响应，定量分析局部冲刷工况下小长径比单桩基础各土反力分量对水平承载力贡献的变化规律，并探讨API 方法的适用性及冲刷深度对土反力曲线的影响。最后基于前文讨论结果，提出考虑基底效应的受局部冲刷海上风电单桩基础简化梁-弹簧计算模型，并通过与三维有限元计算结果的对比，验证该模型预测结果的合理性。

1 考虑局部冲刷坑形态的三维有限元模型

采用有限元分析软件ABAQUS 建立考虑冲刷坑形态的三维桩土相互作用数值模型，如图1 所示。桩基与土体模型均采用三维八节点的缩减积分单元C3D8R，在桩土接触面附近应力较大的区域适当加密网格以保证计算精度。土体侧边界约束水平位移，底边界约束z向位移。此外，为减少边界效应对计算结果的影响，土体模型的直径取为20D，桩基底部以下土层厚度取为5D。桩土接触面的法向设为硬接触以避免穿透，切向则设置为罚函数，摩擦因数 µ=tan(2φ/3)，φ为土体的内摩擦角。桩周的局部冲刷坑为倒圆台形，坑底直径固定为1 倍桩径，其几何形状由冲刷坑坡角β 与冲刷深度Sd共同确定。

图1 有限元模型Fig.1 Finite element model

地基土和桩基的输入参数取值参考文献[9]。土体为硅质砂土，采用工程中常用的M-C 模型描述其塑性，剪切模量为1.9 MPa，内摩擦角为34.9°，浮重度为10.28 kN/m3，泊松比为0.35。桩基直径D=2.75 m，壁厚56 mm，无冲刷时桩基顶部自由段长度e为2D，截面抗弯刚度为88.1 GN·m2。

基于所建立的有限元模型，对入土深度为31.25 m 的单桩基础在局部冲刷深度分别为0、5.0 和7.5 m共3 个试验工况下的响应开展数值仿真，在桩顶逐级施加水平力，并提取桩顶的载荷-位移曲线。图2 为仿真计算值（图中实线）与相同条件下的试验结果[9]（图中点划线）的对比。定性来看，对于同一冲刷工况，桩顶位移相同时，桩顶位移的有限元值与试验值较为贴合，但各级荷载下的偏移程度有所不同。为进一步定量评价有限元模型预测效果，引入Burd 等[19]提出的评价因子η：

图2 桩顶荷载-位移曲线对比Fig.2 Comparison of pile head load-displacement curves predicted by FE model and centrifuge test

式中：Aref为图2 中曲线2 与x轴所围面积；Adiff为图2 中曲线1 与曲线2 所围面积。η越趋于1 表明两条曲线重合程度越高。计算得到3 个对比工况的η 分别为0.95、0.97 和0.96，说明本文所建立的三维有限元模型能够较好地反映受局部冲刷桩基的水平承载能力变化过程。

2 不同长径比与冲刷工况的设置

由于控制单桩基础水平承载特性的参数往往是长径比而非桩径[17]，故本文研究对象的桩基外径及壁厚与前文已验证的模型保持一致。根据以往设计经验，海上风电大直径单桩基础的入土段长径比通常为6～8，因此，相应设置了具有不同长径比的3 个单桩模型PILE2、PILE3 和PILE4（表1）。桩基在水平力作用下的变形刚柔特性与地基土和桩基的相对刚度有关，Poulos 等[20]给出了如下定义：

表1 仿真桩基参数Tab.1 Pile parameters used in FE model

式中：Es为地基土压缩模量；L为 桩基入土深度；EpIp为桩基截面模量；4.8 与388.6 分别为刚性桩上界和柔性桩下界。根据式（2）可以计算得到上述3 个模型桩基的土/桩刚度比分别为23.66、13.87 和7.49，均位于刚性桩与柔性桩之间，但更接近于刚性（下称偏刚性桩）。为进一步分析入土段长径比对受冲刷桩基水平承载特性的影响，另外设置L/D为16.4 的柔性长桩PILE1 作为对比。

本文设置了无冲刷、局部冲刷及整体冲刷为代表的3 种冲刷形态。冲刷深度往往与桩径、水文条件及海床土类型直接相关，如砂质海床的Scroby Sands风场的4.2 m 直径桩基在安装5 个月后桩周形成深1.38D的冲坑，而黏土质海床的Kentish Flats 风场的5 m 直径桩基的最大冲刷坑深度也达到了0.46D[2]。在缺少实测数据时，API 规范[5]建议桩周局部冲刷坑最大冲刷深度Sd取为1.5D，冲刷坑坡角 β取为30°。为不失研究的一般性，本文中的局部冲刷和整体冲刷工况参考API 规范各设置了0.5D、1.0D及1.5D共3 种冲刷深度。冲刷工况见表2，与表1 中所列的4 种不同长径比桩基两两组合，总计形成28 组仿真工况。

表2 仿真冲刷工况设置Tab.2 Scour cases used in FE model

3 冲刷对桩基承载特性的影响

3.1 冲刷形态对桩基响应的影响

冲刷坑形态对水平受荷桩基的桩身响应具有一定影响。图3 对比了PILE2（L/D=8）在不同冲刷工况下的桩顶载荷-位移曲线。从图3 可见，随着桩周冲刷坑深度的增大，桩基的承载力随之下降。然而，当冲刷深度相同时，受整体冲刷桩基的承载力显著小于受局部冲刷的桩基，这表明忽略局部冲刷坑形态将显著低估桩基水平承载力。

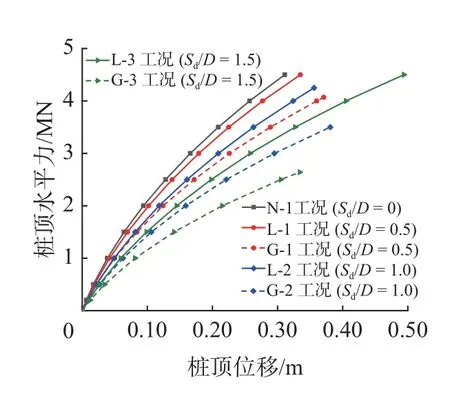
图3 PILE2 桩顶荷载-位移曲线对比Fig.3 Comparison of pile head loaddisplacement curves of PILE2

为进一步分析长径比对桩身响应的影响，计算PILE1 和PILE4 在3 MN 水平力作用下，不同冲刷工况对应的桩身响应。从图4 可见，PILE4 在水平力作用下绕转动中心O旋转，呈现明显的刚性桩特征；而PILE1 的桩身位移曲线则出现竖向切线，整体表现为柔性桩特征。虽然不同柔度桩基的桩身变形均随着冲刷深度增大而增大，但也显然可见冲刷坑形态对偏刚性桩的桩身位移影响更大。当局部冲刷深度达到1.5D时，PILE4 的桩顶位移已经达到了未冲刷时的2 倍，而与之对应的PILE1 则只增长了30%，这意味着小长径比桩基对冲刷坑形态更为敏感。

图4 不同冲刷坑形态对PILE4 和PILE1 桩身变形的影响（F=3 MN）Fig.4 Influences of different scour pit’s shapes on deflection of PILE4 and PILE1 (F=3 MN)

海上风电单桩基础一般为长径比小于10 的偏刚性桩[21-22]，水平承载特性接近于PILE2 和PILE4，并以侧向承载为主；导管架基础的桩基则因考虑抗拔性能而增大桩长，大多属于柔性长桩，桩基水平承载特性接近于PILE1，且通常以竖向承载为主[23-24]。结合上述对比结果看，单桩基础比导管架基础在设计时更需要考虑冲刷坑形态的影响。

3.2 长径比对受局部冲刷桩基承载力组成的影响

文献[17]在分析了于欧洲北海沿岸开展的大直径单桩基础现场试验数据后，认为大直径单桩基础的水平承载力由桩侧土反力、基底水平力与力矩及桩侧垂向摩阻力共同组成，其受力分析如图5 所示。传统API 方法仅考虑了桩侧土反力，忽略了其余分量的贡献，可能会低估小长径比单桩基础冲刷后的承载力。因此，有必要定量分析海上风电单桩基础在冲刷前后各土反力分量在承载力中占比的变化，以此进一步讨论API 方法的适用性。

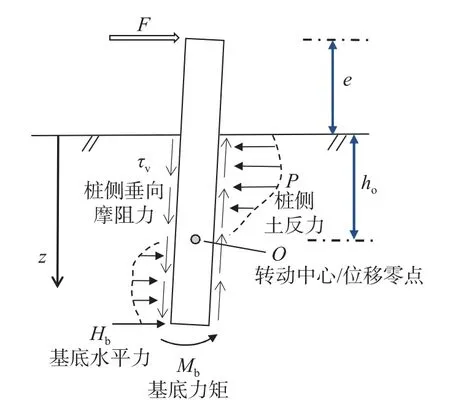
图5 水平受荷桩受力分析Fig.5 Free-body diagram of lateral loaded pile

从有限元计算结果中提取桩身指定截面的剪力值，利用Python 编写程序拟合桩身的剪力分布，并对其求一阶导数得到桩侧土反力p的分布表达式。并从有限元模型中导出作用于桩基的其余土反力分量（基底水平力、力矩及桩身垂向摩阻力）。根据图5，水平受荷桩的静力平衡条件有：

式中：ho为 桩基转动中心O（或位移零点）到泥面距离；e为桩顶水平加载点到泥面距离；L为桩基入土深度；F为水平作用力，其余符号物理意义参见图5。根据上述平衡方程，对所获取的桩基土反力值进行校核，等式两侧误差小于5%时表明提取值合理。

为定量研究不同土反力分量对水平受荷桩抗倾覆能力的贡献，参考Wang 等[25]的计算方法，将各土反力分量i对点O取矩得到Ms,i，并把其与外力矩F(e+ho)之 比作为水平承载力贡献占比Rs,i，计算式为：

图6 为不同局部冲刷工况下，PILE2（L/D=8.0）的基底水平力、力矩与桩侧竖向摩阻力对桩基承载力的占比。从整体变化趋势看，随着局部冲刷深度的增大，桩基入土段长径比也逐步减小，桩基水平承载特性向刚性桩过渡，基底水平力、力矩及桩侧摩阻力对桩基承载力的贡献随之增大。其中，基底水平力占比最高达到9%，紧随其后的是基底力矩。但桩侧垂向摩阻力相比前两项（二者总和约为10%）依然较小，不足1%，对桩基响应计算结果影响较小（与文献[25]结论一致），故下文将其忽略。

图6 不同冲刷工况下 Hb、Mb与τv对PILE2 水平承载力贡献Fig.6 The contributions of Hb、Mb and τv to the lateral bearing capacity of PILE2 under various scour cases

图7 为不同长径比桩基的基底效应随局部冲刷深度的变化曲线。达到最大冲刷深度时，柔性桩（L/D=16.4）基底效应对承载力的贡献仅占1.5%，而长径比6～8 的偏刚性桩却已经达到10%左右，基底效应对桩基水平承载力的影响不能被忽略。传统的API 曲线方法由于只构建了桩侧土反力弹簧，会低估偏刚性桩的水平承载力，尤其在考虑局部冲刷后，桩基入土段长径比进一步减小，导致API 法难以准确预测局部冲刷后海上风电单桩基础水平承载能力。

图7 不同长径比桩基基底效应对桩基水平承载力的贡献Fig.7 Variation of proportions of pile base effects to the horizontal bearing capacity of pile

3.3 局部冲刷对土反力曲线的影响

土反力曲线是桩基计算的重要边界条件，只有定量分析冲刷对土反力曲线的影响，才能合理预测冲刷后的桩身响应。有学者[26-27]认为：局部冲刷坑形成后，由于坑底泥线以上覆土层的存在，土体破坏模式发生了改变，桩前待推动的地基土楔形体体积增大，进而导致局部冲刷时的侧向土反力相对整体冲刷增大。Lin 等[28]、Qi 等[9]分别基于理论分析和离心机试验研究了冲刷坑形态对p-y曲线的影响，引入了等效深度ze代 替原有的相对深度z′代入p-y曲线计算公式中，得到考虑局部冲刷修正后的p-y曲线，相应的等效深度ze曲线如图8 所示。

图8 等效深度概念图示Fig.8 Schematic sketch of equivalent depth

根据图8 可得出：考虑上覆土层存在的修正py曲线的等效深度ze满 足ze≤z′+Sd=z，即计算点冲刷后的等效深度ze始 终不大于冲刷前的深度z。但当局部冲刷深度为1.5D时，Qi[9]给出的p-y曲线受冲刷影响的深度为1.5D左右，而Lin[28]给出的则达到了7.0D，二者相差较大。事实上，由于Lin[28]采用的布氏解是以集中荷载作用于半无限空间弹性体表面为条件得到的，忽略了土体的塑性，表层土中竖向有效应力的计算值相较于实测值往往偏小[29]，故相较于Qi[9]的试验结果给出了更为保守的冲刷影响范围。

为确定冲刷对海上风电单桩基础p-y曲线影响的深度范围，根据前文从有限元中导出的结果，选取PILE3（半刚性桩）和PILE1（柔性桩）在局部冲刷工况L-1、L-2 下z′深度处与无冲刷工况N-1 下z′+Sd（z）深度处的p-y曲线进行对比，结果分别如图9 和图10 所示。可见，随着z′的增大，冲刷前z深度处的p-y曲线与冲刷后z′深度处的曲线趋于重合，且在z′/D≤0.5的范围内，二者相差也较小。故可以认为，对于同一计算点可以继续沿用冲刷前的p-y曲线作为局部冲刷后的p-y曲线。

图9 PILE3 冲刷前后同一深度处p-y 曲线对比Fig.9 Comparison of p-y curves for PILE3 at the same depth before and after scour

图10 PILE1 冲刷前后同一深度处p-y 曲线对比Fig.10 Comparison of p-y curves for PILE1 at the same depth before and after scour

同样地，为分析不同冲刷工况对偏刚性桩基底土反力曲线的影响，图11 对比了PILE3 在局部冲刷坑深度0 到1.5D范围内的Hb-vb（基底剪力-基底位移）及Mb-θb（基底弯矩-基底转角）曲线。图11 表明，考虑计算误差等因素在内的影响，单桩基础的基底土反力曲线在本文所设置的冲刷深度范围内基本保持不变。这是由于局部冲刷仅显著削弱了表层土的土压力，而桩底位置的深层土体受到影响较小[28]，故深层p-y曲线和基底土反力曲线在冲刷前后变化小。

图11 PILE3 基底土反力曲线Fig.11 Pile base soil resistance curves of PILE3

4 受局部冲刷海上风电单桩简化梁-弹簧模型

尽管DNV 规范[4]推荐在设计中采用三维有限元分析，但其计算量通常较大，并不适用于实际工程中的早期评估和快速迭代设计。根据前文的讨论结果，本文参考Byrne 等[17]基于Winkler 假定（弹性地基梁模型）改进的四弹簧模型，建立如图12 所示的受局部冲刷海上风电单桩基础简化梁-弹簧计算模型。在缺少实测数据时，采用无冲刷三维有限元模型中提取的土反力曲线作为各弹簧对应的刚度曲线，通过减少单元计算数量，对多种局部冲刷工况下的桩基响应实现快速预测。

图12 受局部冲刷海上风电单桩基础的简化梁-弹簧计算模型Fig.12 The simplified beam-spring model for OWT monopile subjected to local scour

由于桩侧竖向摩阻力对承载力贡献很小，因此该桩土相互作用模型由其余3 组土弹簧组成，分别是桩侧p-y弹簧、桩底Hb-vb和Mb-θb弹 簧。当发生局部冲刷时，原始泥面以下Sd范围内不再建立桩侧p-y土弹簧单元。依照前文所述，由于局部冲刷对剩余土弹簧的影响较小，故其位置和刚度特性保持不变。

为验证本文中所提出模型的合理性，基于ANSYS APDL 参数化语言建立受局部冲刷作用的海上风电单桩基础简化计算模型。桩身采用两节点的BEAM 188 梁单元，土弹簧则采用能够描述非线性刚度的COMBIN 39 单元，并通过修改关键字设置来定义一维扭转弹簧，从而模拟桩底土反力矩作用。

图13 和图14 分别给出了不同局部冲刷深度下，简化模型及三维有限元模型计算得到的PILE3 桩顶荷载位移曲线和桩身响应曲线。此外，添加工程中常用的整体冲刷模型计算结果（图中虚线）作为对比，该模型忽略了冲刷坑形态并只计入侧向土反力对水平承载力的贡献。

图13 不同模型对PILE3 桩顶载荷-位移曲线计算结果对比Fig.13 Comparison of pile head load-displacement curves of PILE3 predicted by different models

图14 不同模型对PILE3 桩身变形与弯矩计算结果对比（F=3 MN）Fig.14 Comparison of deflection and moment along PILE3 predicted by different models (F=3 MN)

由式（1）计算得到本文提出的简化模型相对于有限元模型在L-1、L-2 和L-3 共3 个冲刷工况下，桩顶载荷-位移曲线的 η值分别为0.97、0.96 和0.94，误差小于10%，满足工程要求。因此，本文模型比较合理地反映了考虑局部冲刷后的单桩基础水平承载特性。但局部冲刷坑的深度较大时，由于长径比减小会导致桩侧垂向摩阻力占比增大，使简化模型所预测的桩基承载力相较于有限元结果略为偏低。

对比整体冲刷模型的计算结果也可发现，忽略上覆土层及基底效应的影响使桩身位移和桩身弯矩偏大，并且随着冲刷深度的增大有进一步扩大的趋势。冲刷深度达到1.5D时，桩基的水平承载力不足其余两模型预测值的1/3，在3 MN 水平力作用下已经失稳。因此，相较于本文提出的简化模型，工程中常用的整体冲刷模型偏于保守，不能合理反映局部冲刷后海上风电单桩基础的水平承载特性。

限于本文研究内容，该简化模型适用于冲刷坑形态固定为倒圆台形且冲刷坑深度不大于1.5D的砂土地基中大直径单桩基础的侧向承载力评估。在实际工程应用中，冲刷坑形态以及海床地质复杂多变，本文所提模型对不同冲刷坑尺寸及黏土地基条件下的大直径单桩计算的适用性，有待进一步研究。

5 结语

本文基于有限元软件ABAQUS 建立了考虑冲刷坑形态的海上风电单桩基础三维有限元分析模型，研究了冲刷坑形态、桩基长径比等因素对海上风电单桩基础侧向响应的影响，提出了考虑基底效应的受局部冲刷单桩简化梁-弹簧模型，得到以下结论：

（1）小长径比水平受荷桩基的侧向响应对局部冲刷坑形态更为敏感。相较于采用柔性长桩的导管架基础，海上风电单桩基础大多为长径比较小的偏刚性桩，因此在设计时需重点考虑冲刷坑形态对单桩基础水平承载力的影响。

（2）对于偏刚性桩，局部冲刷会导致桩基入土段长径比显著减小，基底效应和桩侧垂向摩阻力在桩基水平承载力中的占比将进一步提高，传统的API 方法仅考虑了桩侧土反力的作用，难以准确预测局部冲刷工况下海上风电大直径单桩基础的水平承载能力。

（3）在确定了局部冲刷对深层地基的土反力曲线影响较小的规律后，提出了考虑基底效应的单桩基础简化梁-弹簧模型，通过与三维有限元计算结果的对比，验证了本文模型预测的准确性，而工程中常用的整体冲刷模型由于忽略了上覆土层和基底效应对桩基水平承载力的影响，预测结果偏于保守。