内部激励下的涡旋压缩机动力特性研究

刘 涛，柴正阳，麻德权

(兰州理工大学 机电工程学院，甘肃 兰州 730050)

1 引言

涡旋压缩机相对于其他容积式压缩机具有高效、低噪、振动低等优点，广泛应用于空调制冷、动力工程和交通运输等领域[1]。涡旋压缩机的动力学性能是影响涡旋压缩机运行平稳性和可靠性的重要因素。

涡旋压缩机曲柄轴与动涡盘连接处多采用无内圈滚针轴承联接，系统的运动副不可避免的产生大小不同的间隙，这些间隙常存在轴承和防自转机构等地方，间隙会导致涡旋运动副产生泄漏/碰撞；高速运转状态下，受气体力大小的影响，曲柄轴与轴承间的接触力随旋转角度发生周期性的变化，引起转子与轴承接触刚度的变化，产生冲击动载荷，从而造成转子机构的振动和噪声，加剧零部件的摩擦磨损并缩短使用寿命，降低了机构可靠性和工作寿命。

张春等[2]通过ANSYS软件建立了涡旋压缩机转子系统的虚拟模型，涉及到轴承的刚度、小曲拐和动涡旋盘的柔性等因素，得到了实际工况时曲轴和动涡旋盘的应力、应变，以及实际与理想工况下各构件运动副反力，但未考虑在刚度变化及间隙存在的情况下，对转子系统的分析；赵嫚等[3]考虑到接触副间隙及模型柔性，构建了含运动副间隙及柔性的涡旋压缩机转子系统虚拟样机模型。并利用ADAMS软件中进行动力学仿真，分析动涡盘倾覆力作用下运动副间隙及构件柔性对驱动轴承动力学特性的影响，但未利用转子在工作状态下与轴承之间时变刚度引起的动力学变化；Tae-jong Kim[4]采用有限元和传递矩阵相结合的方法研究了CNG压缩机转子-轴承系统的动力学行为，表明了在旋转运动中，考虑不平衡力和外压缩力的曲轴轨迹比只考虑不平衡力的曲轴轨迹更大。

目前国内外学者对涡旋压缩机的时变刚度与间隙耦合激励的研究相对较少。本文以某涡旋压缩机转子系统为研究对象，通过涡旋压缩机驱动轴承在时变刚度及间隙激励下，对涡旋压缩机转子系统进行动力学分析，分析滚子轴承的受力情况，建立涡旋压缩机三维虚拟样机模型，数值求解驱动轴承的时变刚度模型，联合Adams动力学仿真分析，进而分析出耦合时变刚度和运动副间隙对转子系统的影响，为涡旋压缩机高效平稳的运行提供理论支持。

2 驱动轴承时变刚度和间隙耦合模型

2.1 动涡盘受力分析，图1

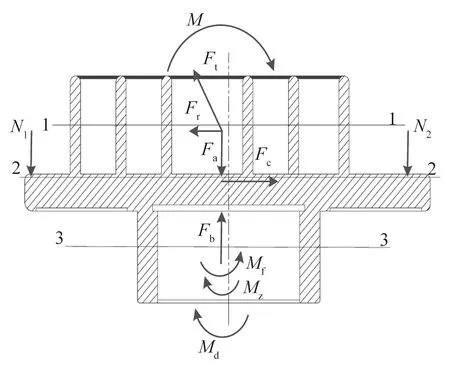
图1 动涡盘受力

动涡旋盘在工作过程中，工作腔内受到来自于压缩气体的径向气体作用力Fr，切向气体作用力Ft，轴向气体作用力Fa；Fc为涡旋盘的离心惯性力，M为倾覆力矩，Mz为自转力矩，Mf是防自转十字滑环提供的防自转力矩。

本文以渐开线涡旋盘作为研究对象，根据理论计算，涡旋盘受各力计算公式如下

(1)

(2)

式中ε1=Pd/Pq

εi——各相邻压缩腔之间压力比

ps——吸气压力

P——节距

h——涡旋齿高度

2.2 轴承受力分析

轴承内圈收到曲柄轴承的驱动力，涡旋盘中的径向气体作用力Fr，切向气体力Ft及动涡盘的惯性向心力Fc。

图2中各作用力满足以下关系

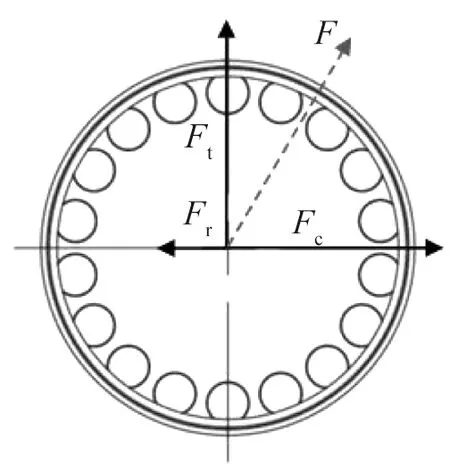
图2 驱动轴承受力

(3)

2.3 曲柄轴与滚子接触面受力分析

曲柄与轴承之间间隙相对于轴承直径很小，如忽略滚针轴承径向间隙，则曲柄轴与滚子直接接触，曲柄轴与滚针轴承之间的接触载荷为Qz，其中在接触区域的中间滚子具有最大的接触载荷Q0，在最大载荷处两边与曲柄轴接触的滚子载荷分别为Qi和Qi′(i=1，2，3，…，i′=1，2，3，…)。

(4)

由文献[5]得到近似公式

Qi=Q0×cosγi

(5)

则有

(6)

则最大载荷

(7)

3 时变刚度模型的建立

3.1 单滚子刚度分析

3.2 曲柄轴与滚子之间刚度

压缩机正常运转中，接触副之间产生里的作用，若只考虑弹性变形，计算弹性问题，则按照Hertz线接触问题的弹性变形量亦称弹性趋近量δ，Palmgren给出了钢制滚子的经验公式[8]

(8)

式中Q——滚子载荷

Lwe——滚针有效长度

根据文献[5]给出了Palmgren经验公式修正后的公式(9)

(9)

对上式求导得出单滚子接触刚度Ki为

(10)

式中Lwe——滚针有效长度

D——当量直径

D1——轴承外圈直径

d1——滚针直径[6]

3.3 滚针轴承总刚度模型

在保守系统中，势能U是关于广义坐标qj的一个函数[7]，将势能U围绕平衡位置进行泰勒级数展开得到如下关系

(11)

该接触副系统为弹性接触系统，根据小阻尼震荡衰减理论在平衡位置的级数展开的二阶后的想可以去掉，则势能方程可化简为

(12)

其中K——刚度矩阵

q——广义坐标矩阵

Kij——广义刚度

(13)

对于滚针轴承系统，涡旋压缩机在工作过程中，曲柄轴与轴承的接触载荷由轴承中的部分滚子共同承担，设参与滚子的数量为n0。

则有总势能为单个滚子弹性系统的势能和，即

(14)

轴承滚子的弹性接触法向载荷为

(15)

则有轴承的广义刚度为

(16)

单个滚子的刚度

(17)

则有

(18)

滚子与曲柄轴及轴承外圈的接触属于线接触，载荷方向为滚子的法向，其中位置i的滚子的受力以轴承端面xOz为坐标平面，可有位移矩阵为q={δx，δZ}T

δi=δx+δz

(19)

则

δi=δxsinγi+δzcosγi

(20)

固有

(21)

3.4 求解时变刚度曲线

本文以a=4.7 mm，h=11 mm，p=18.84 mm，ps=0.3 MPa，α=45°，n=2900 r/min的某一车载涡旋压缩机为例，以滚针轴承与曲柄销接触为研究对象，忽略滚针及其接触材料差异，表1列出了无内圈滚针轴承的何参数。

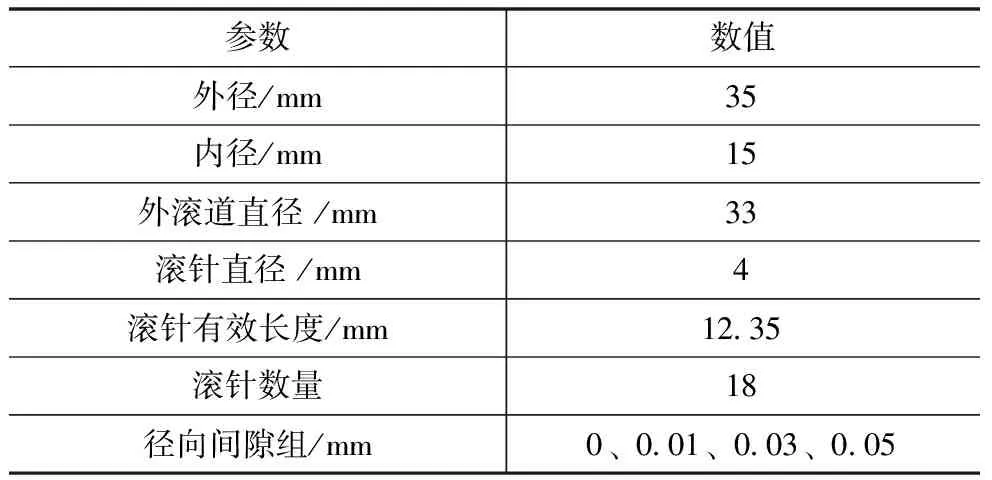
表1 滚针轴承几何参数

由于负载涡旋盘受到时变气体力及动涡盘转动时惯性力的作用，曲柄销与驱动轴承之间的接触力产生周期性的变化，根据本文接触刚度理论，曲柄销与驱动轴承间接触刚度随之发生周期性变化；根据本文驱动轴承径向接触刚度计算方法，数值求解得到驱动轴承接触刚度如图3所示，其中最小接触刚度为1.11×106，最大接触刚度为1.137×106，出现在涡旋盘的开始排气时。

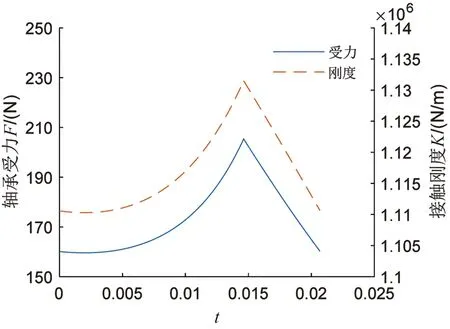
图3 驱动轴承受力及接触刚度

4 耦合间隙及变刚度虚拟模型

4.1 三维实体模型的建立

通过SolidWorks建立涡旋压缩机转子系统模型，主要构件包括动静涡旋盘、 十字滑环、曲轴、轴套、驱动轴承、平衡铁、定轴转子以及机架体，定轴转子转动带动曲轴转动，曲轴销与驱动轴承接触传递驱动力，在十字滑环的约束下，带动动涡盘与静涡盘进行啮合，完成气体的吸气、压缩、排气过程。

考虑到ADAMS中无法对模型接触副间隙进行设定，在建立模型的同时设置一定的间隙，根据本文仿真的要求，在创建模型时取曲柄销与滚针轴承之间的间隙分别为0.01 mm、0.03 mm、0.05 mm，装配完成后，进行干涉性检验，检查是否存在装配不当，将检查合格的样机模型从SolidWorks中输出为x_t格式保存。

4.2 虚拟样机动力学模型建立

将保存好的x_t模型文件导入到ADAMS中，根据模型设置重力加速度为9.8 m/s，对机构中的每一个构件分别进行重命名、材料属性定义，各构件参数如表2所示。

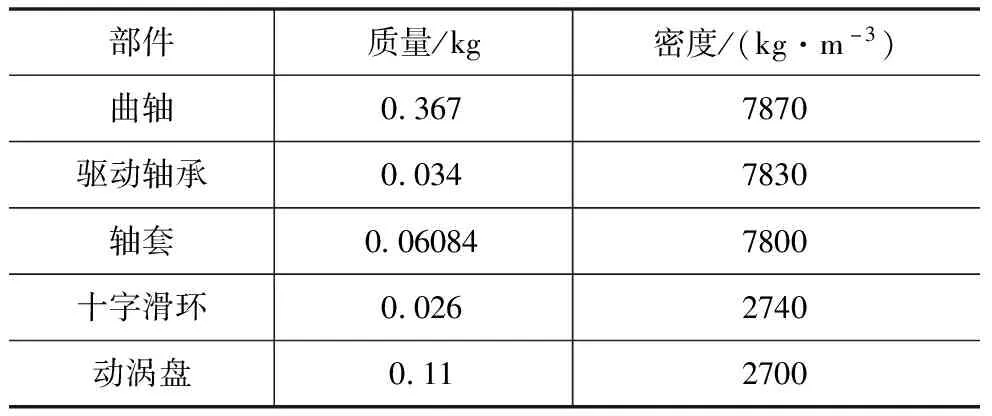
表2 零件材料参数表

根据压缩机实际运行状况对涡旋压缩机模型各接触副之间施加约束及驱动，对于含间隙的驱动轴承与曲柄销运动副采用接触副进行设定，理想旋转副采用转副进行约束，在Adams/view中ground相当于机架[8]，系统各构架之间的约束条件如表3。

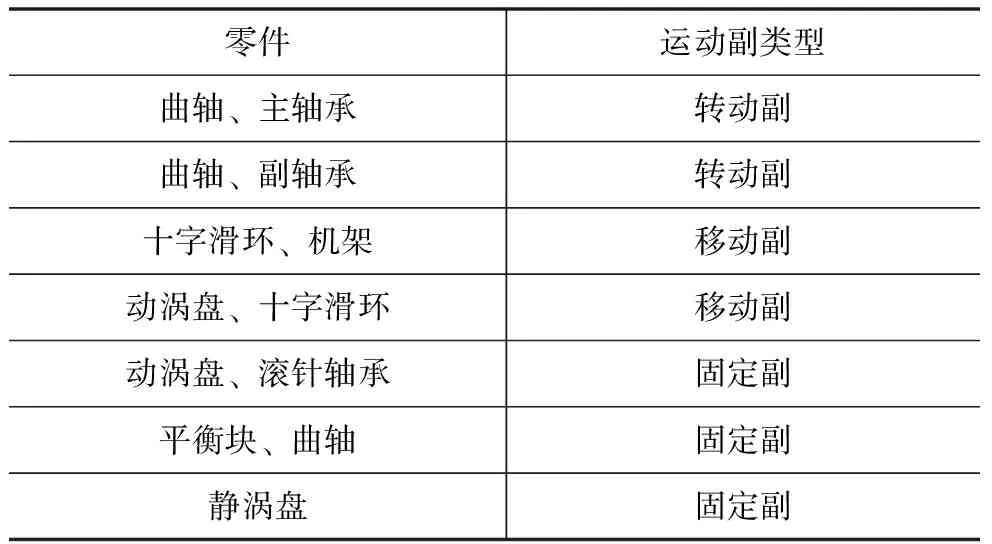
表3 构件约束关系

5 ADAMS仿真分析

5.1 条件的添加

在实际情况下，压缩机在正常工作时，涡旋盘中气体力会对压缩机转子系统产生影响，由于气体力的真实情况太过复杂，本文将涡旋盘中气体力模拟成为轴向及径向单向力，施加于动涡盘1/2涡旋齿高处，忽略倾覆力矩的影响。气体力的添加采用样条曲线进行模拟，利用气体力计算公式及及进行数值计算得到的气体力函数曲线，利用MATLAB工具提取样条数据，将数据添加到ADAMS样条函数数据单元模块，施加到涡旋盘上基圆处，设置单向力随曲轴转动，其中力函数公式中的SPLINE样条拟合曲线根据气体力变化规律建立且随时间周期变化而变化，在SPLINE拟合方法对话框中选择Cubic Fitting Method选项。

驱动轴承与曲柄轴接触设定为impact碰撞接触类型，采用solid to solid的接触形式，其中将接触刚度设定为时变接触刚度，刚度函数采用接触变刚度的曲线拟合函数，本文采用四项多项式函数拟合出时变刚度函数。

5.2 仿真及测量

设置驱动于定轴转子，设置转速为2900 r/min，即在速度函数设置为1.74E+04d*time，仿真步数设置为2500步，仿真时间设置为2个回转周期，一个回转周期为0.02068 s，仿真时间为0.4136 s。设置完之后进行仿真操作，查看模型仿真是否出现错误，没有错误则进行下一步后处理。

在驱动轴承处添加不同的间隙模型分别导入ADAMS/view中分别进行仿真，模型可分为理想接触模型、0.01 mm、0.03 mm、0.05 mm模型，对其分别进行定常接触刚度条件，及变接触刚度条件下分别进行模拟仿真，将得到的不同的仿真结果添加到ADAMS中的后处理模块进处理比较。

首先将仿真接触条件设置为变刚度条件，分别求解出各个间隙模型的仿真结果，在仿真结束后进行后处理，将各个间隙的得到的不同碰撞力曲线添加到同一图幅如图4(a)所示；改变接触条件为定刚度，得到碰撞力曲线如图4(b)所示；变刚度和定刚度条件下的接触副碰撞力曲线图进行比较得知，不同刚度条件下，接触副接触碰撞力有所不同，且曲柄轴与轴承的碰撞频率也有很大区别。

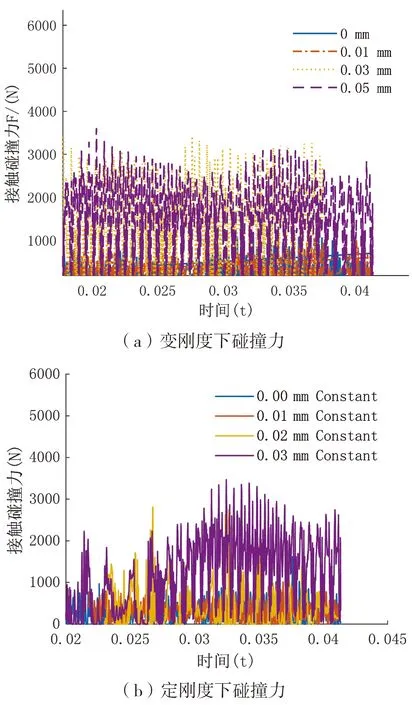
图4 接触碰撞力对比

图4(a)为曲柄轴与轴承在时变刚度与间隙共同条件下的接触副碰撞力曲线比较图，其中理想模型曲线与间隙模型存在着较大的区别，随着接触副间隙的增加，接触碰撞力幅值增大，阶跃周期减小，碰撞频次增多。在0.03 mm间隙下第二周期稳定区间，接触碰撞力的最大幅值达到3420.65 N，而在无间隙下碰撞接触力最大幅值为1153.67 N，前者最大碰撞力是后者的2.96倍；定刚度接触副周期内碰撞次数随着间隙的增大，呈现递减的现象，直至间隙为0.005 mm处，接触副处于时刻接触状态，变刚度与定刚度相反，接触副周期内碰撞次数随着间隙的增大，呈现倍增的现象，这是由于在变刚度与间隙的自激力影响下导致碰撞力的频次增大。

不同刚度工况下，碰撞力幅值相差不大，时变刚度碰撞力略大于定刚度碰撞力幅值，碰撞频次呈现不同的现象，间隙的存在对接触碰撞力幅值的影响较大，随着接触副间隙的增大，接触碰撞力幅值变大，对系统的稳定性影响显著见表4。

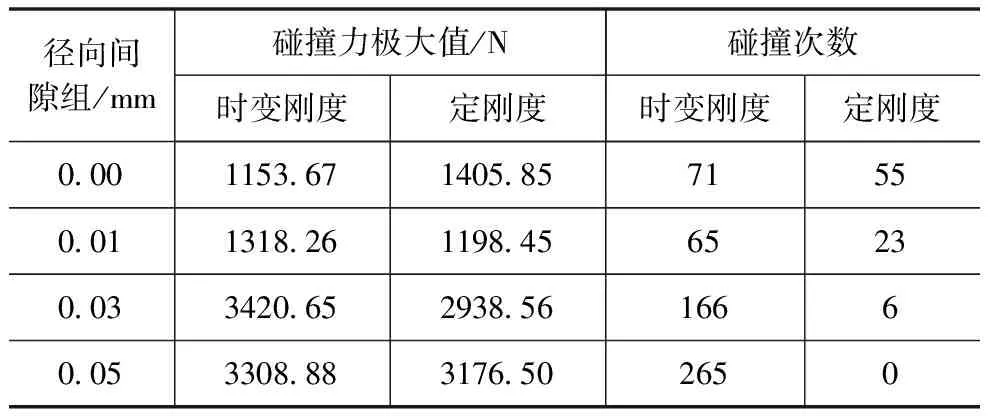
表4 碰撞数据对比表

图4中0.03 mm间隙与0.05 mm间隙条件下的碰撞接触力大小近似，碰撞频率相近，但0.05 mm间隙下碰撞更快的进入周期接触区间，两种间隙下碰撞力幅值相差不大，0.003 mm具有更多的特征，故将在0.03 mm下进行变刚度与定刚度下的接触碰撞进行比较。

图5为0.03 mm间隙下定常刚度与变刚度接触下的接触碰撞力曲线图，由图可以看出变刚度下的碰撞力曲线趋于稳定的周期变化，并比较定常刚度变化频率更高，碰撞的次数增加，且多处于碰撞状态，由此可知变刚度使得碰撞接触力的幅值增加，且碰撞力阶跃更加的规律，频次更高。

图5 定常刚度与时变刚度接触力比较

图6为驱动轴承的位移图及局部放大图，驱动轴承在变刚度及间隙下的位移出现波动，且不同间隙下波动有较大的区别，围绕理想状态位移波动，整体位移幅度在-0.2 mm至+0.2 mm之间波动，在时变刚度工况下，驱动轴承的位移出现轻微的周期波动会加剧工作区域的不稳定性，造成压缩气体的泄漏及给系统造成振动及噪声。

图6 驱动轴承位移

图7为0.03 mm间隙下主轴承质心加速度图像，由图可知在变刚度接触下主轴承加速度幅值为定刚度幅值的1.45倍，相同间隙曲柄轴与驱动轴承在变刚度工况下对压缩机整体的影响更大，由此接触副在时变刚度与间隙工况下涡旋压缩机转子系统具有更大的振动加速度，造成涡旋压缩机整体产生振动。

图7 主轴承振动加速度

接触碰撞力在变刚度及间隙共同耦合情况下，随着间隙值增大，碰撞力的幅值变大，碰撞力的阶跃变化趋于均匀，且在变刚度的作用下较定刚度接触力变化的幅值及频率增加，且具有稳定的周期碰撞振动。

5 结论

(1)涡旋压缩机驱动轴承受到动涡盘中周期变化的气体力的作用，导致曲柄轴与轴承接触的刚度随着气体力的变化产生周期性的变化，本文采用能量法绘制出时变刚度的变化曲线，对涡旋压缩机动力学系统分析提供了理论及方法的支持。

(2)定刚度条件下，曲柄销与轴承接触间隙的存在使得接触副之间的接触碰撞力幅度增大，随着间隙的增大，接触副周期碰撞次数减少，接触副间由于碰撞造成的冲击载荷降低，在 0.005 mm间隙下周期碰撞次数减少至0，故由高频碰撞转变为接触副时刻接触状态，冲击载荷减弱。

(3)耦合时变刚度及间隙共同条件下，接触碰撞力较定常刚度有更大的幅值，0.003 mm间隙下碰撞力为定刚度的1.16倍；与定刚度下接触碰撞随着间隙的增大趋于进入稳定的脉冲接触区不同，接触副周期碰撞次数增多，由71次增至265次，加大了轴承接触副间的冲击载荷；且变刚度激励下主轴承振动加速度为定刚度的1.45倍，大大降低了压缩机整体系统的稳定性。