全啮合双涡旋齿涡旋压缩机齿形分析与流场模拟

韩 奕，潘诗洋，王 君，任纯吉，赵玺皓，赵 鑫，崔 冬

(1.中国石油大学(华东)新能源学院，山东 青岛 266580；2.压缩机技术国家重点实验室，合肥通用机械研究院有限公司，安徽 合肥 230031)

1 引言

涡旋压缩机具有结构紧凑、噪声低、运行平稳等优点，因而其广泛应用于制冷、空调和热泵系统中。提高涡旋压缩机的体积比、压缩比和效率，可以大大提高空调制冷系统的性能。涡旋的型线特征是影响涡旋压缩机的工作性能的主要因素之一[1]。郝胜利[2]提出了一种涡旋压缩机型线方程反求方法，此方法可以用于求任意给定涡旋盘中涡旋型线的数学表达式。张庆庆[3]提出了的一套圆渐开线型线中基圆半径等参数的测绘方法。众所周知，圆渐开线、正多边形渐开线、阿基米德螺旋线和代数螺旋线都可以作为涡旋型线。其中，圆渐开线的应用最为普遍[4]。然而，由单一型线(如圆渐开线)形成的涡旋，不能在涡旋中心区域(或称为涡旋齿齿头部位)实现完全的啮合，而且在加工过程中还会出现刀具干涉现象，最终导致齿头处形成尖点，降低了涡旋齿的力学性能[5]。这个问题可以通过齿头型线修正来解决。

关于涡旋型线的修正，Morishita等人[6]首先提出了一种齿头修正的涡旋型线，其中心区域的内外涡旋型线由一对圆弧平滑连接，进而使2个涡旋完全啮合。随后，Lee和Wu[7]使用两种圆弧和直线来修正涡旋型线，并可以通过改变修正参数来调整涡旋齿的厚度。Liu等人[8-9]利用平面轨道机制定理建立了一个由半径可变的圆渐开线组成的涡旋型线的几何模型。Bell等[10]研究了基于圆渐开线的单圆弧、双圆弧和圆弧线修正模型的几何理论。Wang等[11-12]提出、建模并分析了一种全新的全啮合涡旋型线设计方法。

涡旋压缩机的工作过程通常采用实验或仿真的方法进行研究。王训杰[13]采用动网格对涡旋压缩机的内部流场进行数值模拟，发现径向间隙对涡旋压缩机工作腔内的压力及温度分布、出口温度及输出流量都有一定的影响。根据涡旋压缩机特殊的几何特性，Pereira等人[14]开发了可以根据旋转角度自动调整计算的网格，并将其应用到可以预测工作腔内气体流动和传热的数值模型中。研究发现，气体的温度变化是由压缩过程和气体与工作腔之间的对流换热引起的。Kim等人[15]基于“双边界技术”生成了二维结构化网格，该技术使网格点可以根据边界的移动而移动，以适应网格变形。邱凯[16]对不同转速下空调用涡旋压缩机的功率谱和压力进行了测试，并分析其对压缩机压力脉动、功率损失的影响。

采用双涡旋可以显著提高压缩机的体积流量，同时降低滑动摩擦速度。但双涡旋压缩机的内容积比相对较小，并且在涡旋齿的制造过程中，中心区域的刀具干涉更为严重，也会削弱中心区域涡旋齿头的强度。通过对双涡旋的型线进行修正，可以有效地解决上述问题。涡旋齿的齿头型线修正是指设计出完全啮合的型线，以提高内容积比和压缩比，提高双涡旋的强度。因此，双涡旋型线修正比单涡旋型线修正更重要。

本文建立了双涡旋齿的解析模型，并对双涡旋与单涡旋压缩机的体积流量、内容积比和相对滑动速度进行了对比。为了提高双涡旋压缩机的内容积比，提出了一种新型的修正双涡旋结构，利用一对圆弧修正双涡旋齿的齿头部分，并对齿头修正后的双涡旋压缩机的工作过程进行了数值模拟。这些内容对大体积流量的双涡旋压缩机的设计和开发具有重要意义。

2 双涡旋压缩机的解析模型

2.1 双涡旋齿结构的生成方法

图1所示的双涡旋的基体型线为圆渐开线。其中动涡旋和静涡旋都具有形状相同的2个涡旋齿，并且两组涡旋齿对称地分布在各自涡旋盘的中心点O周围。由于双涡旋结构的对称性，双涡旋的质心位于涡旋盘的中心，这有助于提升涡旋盘的动平衡性能。

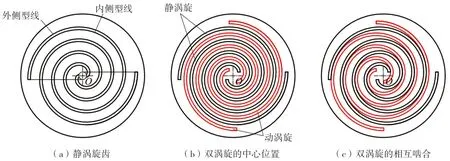
图1 双涡旋的结构

在双涡旋压缩机的装配中，动涡旋齿相对于静涡旋齿旋转π/2，然后偏移Ror的距离，并插入静涡旋中。这一特点不同于单涡旋齿。结果表明，双涡旋压缩机相邻工作腔之间存在 π/2相位角差，并在工作过程中形成了4组工作腔。以 π/2相位差对动涡旋和静涡旋进行装配，可同时实现4个涡旋齿的啮合。

2.2 双涡旋齿的几何模型

由圆渐开线构成的双涡旋的主要几何参数包括渐开线起始角α、渐开线基圆半径Rb、节距Pt、渐开线终止角φe、涡旋齿厚度t、涡旋盘外径Rw，如图2所示。

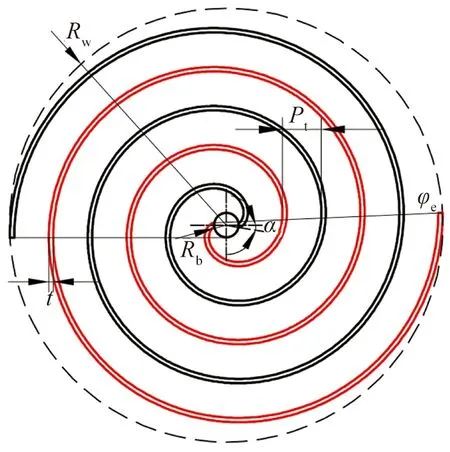
图2 双涡旋齿的结构

渐开线起始角必须满足以下条件

α<π/4

(1)

涡旋齿厚度t可表示为

t=2αRb

(2)

双涡旋的回转圆半径、涡旋盘外径Rw、截距可以被表示为

(3)

(4)

Pt=πRb

(5)

涡旋圈数N可以表示为

N=φe/2π

其中Rb——渐开线基圆半径

Pt——涡旋盘的截距

t——卷轴的厚度

φe——渐开线端角

Rw——涡旋盘外径

n——转速

H——涡旋齿的高度

θ——动涡旋所连曲轴转过的角度

经推导，最大吸气体积Vs和最小排气体积Vd为

(7)

(8)

双涡旋压缩机的体积流量Qv可表示为

Qv=Vsn

(9)

式中εV——内容积比

L——泄漏线长度

3 全啮合双涡旋的几何模型

本节建立了由一对圆弧修正的全啮合双涡旋齿的几何模型。此外，还推导得到了这种全啮合双涡旋的修正参数之间的几何关系与数量关系。

3.1 全啮合双涡旋的齿头修正

所提出的修正双涡旋，或称全啮合双涡旋，如图3所示。以基圆圆心O为原点建立坐标系。外侧渐开线和内侧渐开线上的两点I2和I1，其展开角分别为φ和φ+π/2。渐开线的基圆的切线都经过这两点。

图3 用圆弧修正的全啮合双涡旋齿

计算出小圆弧半径和大圆弧半径Rx和Rd的值，分别得到这2条弧在两条切线上的中心点F1和F2。以F1、F2两点为修正圆弧的圆心，从I2、I1两点开始，可画出I2Q、I1Q两个修正圆弧且2条圆弧相交于点Q。

关于修正双涡旋齿的加工问题，只要修正圆弧半径大于刀具半径，涡旋齿头就不会产生刀具干涉现象。随着修正后的涡旋齿头厚度的增加，其刚度和强度也会随之增加。因此，型线修正可改善双涡旋齿齿头部位的力学性能。

3.2 几何参数对修正双涡旋的影响

3.2.1 圆渐开线起始角α对修正后双涡旋的影响

在h=50 mm，n=3600 r/min，Rb=7.6 mm，Rw=130 mm恒定的条件下，可以得到修正双涡旋压缩机的性能参数的变化情况，如表1所示。显然，Ror的逐渐减小导致了摩擦速度v的减小。同时，渐开线发生角α的增大导致了涡旋壁厚t的显著增大，内容积比εV轻微增大和体积流量QV的减小。

表1 双涡旋压缩机的性能参数随α增加的变化

随着Z齿涡旋压缩机的齿数Z从1增加到5，α，φe，N逐渐减小，而Rb逐渐增大。随着Z的增大，Qv显著增大，εV显著减小，L变化不大。由此可见，在Pt和Rw相同的情况下，增加压缩机涡旋齿数可以显著提高Qv，但εV显著降低。在此情况下，与传统单涡旋压缩机相比，双涡旋压缩机的Qv提高了78%，但εV降低了62%；三涡旋压气机的Qv增加了133%，但εV减小了81%。

还可以看出，随着渐开线初始角α的增大，体积流量Qv减小，内容积比εV增大。Qv和εV的变化趋势相反，因此可以根据实际设计要求，选择合适的修正参数，以满足所需的体积流量和内容积比。

3.2.2 不同修正角γ对修正双涡旋的影响

修正角γ是影响修正双涡旋压缩机性能的重要参数之一。γ决定了最终啮合点B的位置，该点始终位于半径为Rc的圆上。Rc可以推导为

(10)

图4所示为在γ= -7°、3°、20°、40°和63°时，不同修正角γ对修正双涡旋型线的影响。可以看出，随着γ的增大，齿头厚度逐渐增大，但相应地压缩过程会变短。

图4 修正后的双涡旋齿形随修正后的γ角的变化

因为涡旋压缩机的内部流场在任意高度的截面是相同的，所以排气工作腔的投影面积Sd可以反映排气体积。由于涡旋压缩机的涡旋高度是恒定的，因此排出量可表示为

Vd=SdH

(11)

其中Sd——排气工作腔的投影面积

不同修正角γ及其最小封闭容积Sd对应的最终啮合位置如图5所示。随着γ的减小，修正双涡旋的齿头部位的啮合线变长，这会导致排气腔体积变小，内容积比增大。

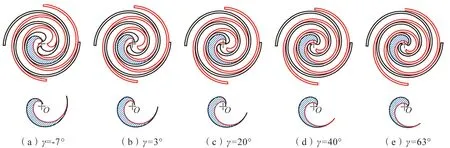
图5 修正后的双涡旋排气腔投影面积随修正后的γ角的变化

图6为工作腔轴向截面积Sd和内容积比εV随修正角γ的变化情况。随着γ的减小，Sd逐渐减小，内容比逐渐增大。当γ值为-7°时，εV可达2.34。

图6 修正角γ随Sd和εV的变化

3.2.3 不同修正展角φ对修正双涡旋的影响

图7给出了修正双涡旋齿头投影面积SD和修正双涡旋压缩比ε随修正展角φ的变化趋势。可以看出，当γ一定时，随着φ的增大，Sd逐渐增大，εV逐渐减小。

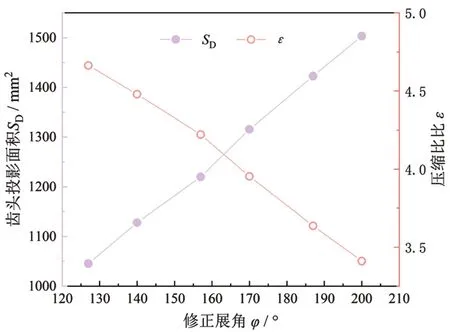
图7 Sd和εV随修正展角φ的变化

随着φ的增加，修正圆弧与基体型线的连接点在每个涡旋中的位置越靠外，最终啮合点的位置也越靠外。当双涡旋齿头的轴向投影面积增大时，齿头的强度会增大。但是，φ的减小也会导致齿头轴向投影面积的减小，即齿头厚度的减薄，导致齿头部位更容易发生变形。

4 涡旋压缩机的工作过程模拟

4.1 温度场及压力场分析

假设图8(a)中的曲轴转角θ为0°，则图8(b)中的曲轴转角为45°。当曲轴旋转45°时，双涡旋压缩机的各个月牙形工作腔依次增压。从图9中可以看出，工作腔1和工作腔2的压力都增加了。在每个瞬时状态下，整个流体域的工作压力也由外向内逐渐增大。此时排气口压力最大，达到310000 Pa。由于双涡旋压缩机的工作过程是周期性变化的，当曲轴再旋转45°时，就会有一个新的工作腔重复上述过程。

图8 修正后的双涡旋压缩机的压力分布

图9 修正后双涡旋压缩机内部速度场

从图8中仍然可以看出，齿头修正后的双涡旋压缩机在运行过程中，压力由外围区域向中心区域逐渐增大。修正后的双涡旋能实现完全啮合，且排气压力明显提高，故而这种压缩机适合于对压缩比要求较高的场合。

4.2 速度场分析

如图9所示，修正后的双涡旋压缩机工作腔内速度分布是不均匀的。可以清楚地看到，每个啮合间隙处都存在气体泄漏。以A、B啮合点为例，A点存在外泄漏的情况，即工作腔向外界的气体泄漏。但这种外泄漏很小，对工作腔压力影响不大。

B点则存在内泄漏情况；即不同工作腔之间的泄漏。可以看出，由于相邻工作腔之间的压差比较大，内泄漏较为严重。

4.3 温度场分析

如图10所示，修正后的双涡旋压缩机工作腔内的温度分布也是不均匀的。很明显，靠近吸气口的工作腔气体温度最低，近似等于吸气温度。然后，随着气体被压缩，温度逐渐升高，直到气体达到排气温度420K。

图10 修正后双涡旋压缩机内部温度场

4.4 双涡旋压缩机的气体压缩过程

气体在依次形成的月牙形压缩腔内逐级压缩，压力逐渐增大，直至涡旋齿头脱啮，气体通过位于涡旋盘中心的排气口逐渐排出。在工作过程中，工作腔内气体压力随旋转角度θ的变化如图11所示。

图11 修正双涡旋的工作过程

从图11可以看出，随着θ的增大，理论绝热压力和模拟压力都在增大，但理论绝热压力值始终小于相应的模拟压力值。这是因为理论绝热压力值是基于不变质量系统得到的，而模拟压力值是基于变质量系统得到的，其中存在气体泄漏。

5 结论

(1)本文建立了以圆渐开线为基体型线的双涡旋齿的解析模型，推导了双涡旋压缩机的结构参数关系式和体积流量计算方程。比较了双涡旋与单涡旋的结构特点和工作过程。研究发现，双涡旋结构可以大大提高体积流量，结构紧凑，动平衡性能较好，但其内容积比大幅降低。

(2)为了提高双涡旋压缩机的内容积比，提出了一种可实现完全啮合的齿头修正的双涡旋压缩机。结果表明，与未修正双涡旋压缩机相比，修正后的双涡旋压缩机的内容积比从1.42提高到1.90，提高了33.8%。由于这些性能的优化，修正后的双涡旋压缩机非常适合用于汽车燃料电池系统等对内容积比要求高的应用场合。

(3)得到了双涡旋压缩机修正参数之间的关系，分析了这些参数对修正双涡旋压缩机性能的影响。修正角γ越小，内容积比越高；修正展角φ越大，涡旋齿齿头强度越大。通过分析修正参数的影响，可以设计出适用于不同应用工况要求下的双涡旋压缩机。

(4)计算了任意旋转角度下压缩腔的容积。并对修正后的双涡旋压缩机进行了数值模拟和工作过程分析。分析了流场的压力和温度分布。数值模拟得到的压缩过程中气体压力始终高于理论绝热过程，这是气体从位于中心区域的高压工作腔泄漏到位于涡盘外围区域的低压工作腔导致的。