涡旋压缩机径向随变机构的限位及转子系谐响应分析

赵 嫚，党江伟，卓俊宝

(兰州理工大学石油化工学院，甘肃 兰州 730050)

1 引言

涡旋压缩机是一种容积式压缩机，因其具有出色的热力学性能以及独特的结构被广泛应用在制冷行业、车载空调、压缩气体和石油化工等的多个领域[1]。

径向随变机构常用于汽车空调领域用涡旋压缩机中。涡旋压缩机的工作依靠动、静涡盘涡旋齿的正确啮合来实现，然而实际工作中由于装配误差、加工误差、腔室积液等现象的存在，动、静涡盘涡旋齿的啮合会出现偏离理想标准状态，采用径向随变机构可以有效地解决这一问题[2]。为减少径向密封力带来的动、静涡齿间的摩擦损失，同时保证径向密封，需对径向随变机构进行限位设计，即将回转半径的改变量限制在一定范围之内。关于涡旋压缩机转子系，苏亚峰研究了不平衡质量大小下的转子稳态不平衡响应特性和变转速下的瞬态不平衡响应特性[3]。赵嫚等人用瞬态不平衡响应分析法分析了转子系统在变转速工况下不平衡质量产生离心力的变化问题以及研究了径向随变机构实际回转半径偏离理论值时主、副轴承的承载情况[4-5]。张亢等人通过优化偏心轮结构参数，降低了由于涡旋压缩机转子系偏心旋转部件惯性力不平衡引起的振动[6]。邱海飞、张晓君等人关于转子系动平衡进行了研究与改进[7-8]。综上，已有研究对于径向随变机构作用下涡旋压缩机转子系的动力特性研究很少，故文章结合带有径向随变机构的涡旋压缩机转子系进行简谐响应分析。

本文以含有径向随变机构涡旋压缩机为研究对象，利用理论建模与数值模拟技术研究转子系的稳态振动，运用定性分析法，通过施加简谐载荷后的响应分析，仿真解决径向柔性机构转子系的可靠性问题，揭示了转子系的振动规律，从而为压缩机稳定可靠的运行提供理论依据和应用基础。

2 径向随变机构的限位方法

十字滑环防自转机构下径向随变机构的限位如图1所示，A为曲柄销中心，在偏心套筒底部设置限位销，当涡旋压缩机以理论回转半径工作时，限位销中心B与静盘中心的轴向投影重合，当限位销中心运行到B1点时，动涡盘中心到达C1点，此时实际回转半径调至最大；当限位销中心运行到B2点时，动涡盘中心到达C2点，此时实际回转半径调至最小。

图1 十字滑环防自转径向随变机构的限位

根据偏心套筒两极限自转角，在主轴加工出和圆柱销能够合理配合的限位孔，就可实现对径向随变机构的限位。

图2为径向随变机构的调节图，图2(a)当理论最大回转半径Rormax=lOC1时，有最大前进转动角

图2 径向随变机构的调节

(1)

图2(b)当理论最小回转半径Rormin=lOC2时，则有最大回退转动角

(2)

圆柱销防自转机构下径向随变机构的限位如图3所示。鉴于实际回转半径必须小于理论回转半径，采用带有的偏心套筒与主轴的配合来约束偏心套筒的回退转动角。lOF为平衡铁内圆弧半径，F点为平衡铁内边上一点在理论回转半径时的位置，偏心套筒带动平衡铁绕曲柄销中心A旋转使得平衡铁内边上一点到达G点，由于这时恰好与主轴相接触，在主轴的制约下，致使偏心套筒上的平衡铁不能够更进一步回转，由此实现了对径向随变机构的限位。GA与FA之间的夹角则是偏心套筒的最大回退转动角δ-。

图3 圆柱销防自转径向随变机构的限位

理论分析先设立一定值求解区间，对任一值，有

(3)

(4)

当偏心套筒转动到限位点时，GA连线与纵轴之间的夹角为

(5)

以A点为坐标原点，G点的坐标为(lFAsinα，lFAcosα)，将G点坐标转换为以O点为坐标原点，并代入到主轴外圆公式：

x2+y2=r2

(6)

如满足公式(6)，即符合理想径向随变机构的限位要求。

涡旋盘自身的几何参数会约束动涡盘的径向位移，圆柱销防自转结构会约束动静盘中心距的改变，当径向随变机构高效实现理想径向柔性时，圆柱销在动静盘侧面之间、动盘之间的摩擦损耗量相等。

3 机构转子系谐响应分析

针对旋转设备，例如汽车发动机、空调压缩机和飞机桨叶等，在旋转时由于结构偏心会产生类似于简谐激励的载荷。这种激励频率与转速有关，如果结构的固有频率和激励频率接近，就会发生共振，从而影响结构的使用，甚至导致结构破坏。为了解决这些问题，需要用到谐响应分析技术，谐响应分析是频域分析方法的一个部分，与结构所受载荷相关，并且结构所受载荷都是简谐载荷[9]，通常验证设计结构能否克服疲劳、共振等影响。

3.1 模型建立

首先根据涡旋压缩机设计参数：基圆半径a=3.024 mm，齿厚t=4.5 mm，齿高h=31 mm，排气角θ*=270°，压缩室对数N=3。应用Solidworks软件进行三维建模，得到如图4所示的转子系三维模型图。

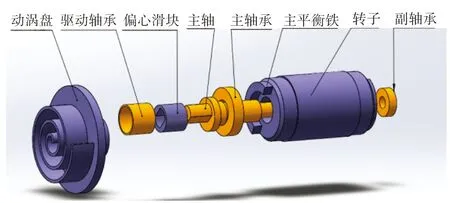
图4 涡旋压缩机转子系三维模型图

3.2 转子系统仿真参数设置

将建立好的带有偏心滑块式径向随变机构的涡旋压缩机转子系三维模型以.x_t格式文件单独保存，然后导入ANSYS Workbench软件中，最后把涡旋压缩机各零件的材料属性输入到工程数据库中，各零部件的材料属性如表1所示。

表1 零件材料参数表

设置好材料属性后，对模型进行网格划分，使用六面体和四面体混合划分法。首先切割涡旋压缩机的模型，切割成相对规则的物体，然后设置整体体尺寸，尺寸为8 mm，最终划分的网格如图5所示，节点数为76757，单元数为43168。

图5 网格划分及质量检查图

经过检查网格质量，得到网格平均质量趋于0.80，由于网格平均值的质量大于0.75，可以进行求解。

进入ANSYS的约束设置界面，添加约束条件如图6。使用ANSYS中的Mass单元添加平衡铁和动盘组件，平衡铁添加在转子上下位置，动盘组件添加在主轴靠近曲柄销的一侧，轴承通过Bearing来进行模拟，轴承X、Y方向的位移和旋转使用远程限制。

图6 边界约束条件

3.3 模态结果分析

由于工程上一般情况只考虑前几阶模态就可以，更高阶的没有实际参考意义[10]，因此以涡旋压缩机的前六阶模态为参考进行分析，得到转子系模态参数的前六阶固有频率和前三阶振型云图。表2为带有径向随变机构的涡旋压缩机转子系的前六阶固有频率，图7所示为转子系和偏心滑块前三阶振型。

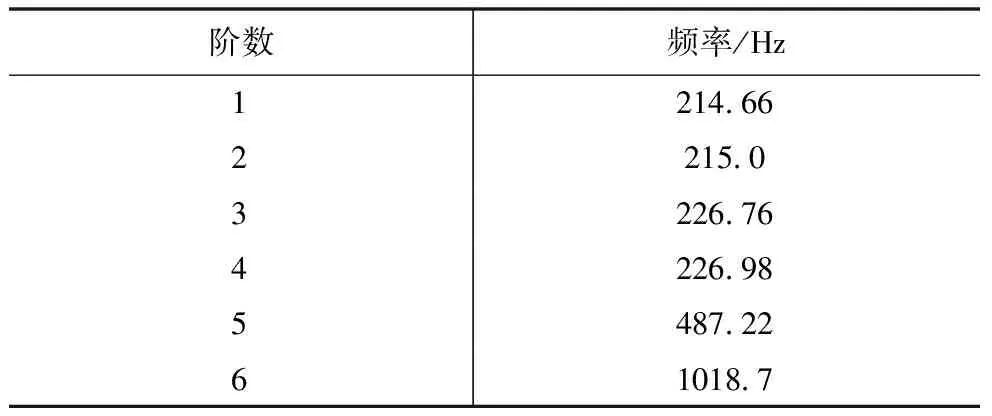
表2 前6阶固有频率

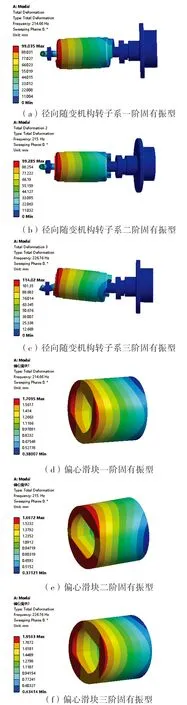
图7 转子系和偏心滑块前三阶振型云图

通过观察表2固有频率和图7振型云图可以得到：一阶、二阶模态固有频率分别为214.66 Hz、215.0 Hz，转子系最大相对变形量分别为99.03 mm、99.28 mm，振动形态主要是轻微的弯曲，在转子靠近副轴承端有集中变形，说明此部位容易发生振动；三阶模态的固有频率为226.76 Hz，最大相对变形量为114.02 mm，振动形态主要为转子系整体的扭转和主轴末端的弯曲，副轴承处有较大变形；偏心滑块前三阶振型云图观察到振型形态均为左右扰动，最大变形发生在主轴靠近曲柄销的区域。从振型云图可以看出机构的单薄环节，对于发生变形量较大的地方，要增大该位置的刚度，在设计和生产机构转子时应考虑到这些薄弱部位，通过改变结构或者选择理想材料属性以达到涡旋压缩机正常运转的目的。

3.4 简谐载荷的施加

结合文中涡旋压缩机设计参数和相关理论计算涡旋盘受到的切向气体力Ft=562.5 N，径向气体力Fr=283.1 N。使用模态叠加法进行谐响应分析，将计算得到的切向、径向气体力施加在主轴曲柄销的中心面，依据模态分析结果得到的模态参数，确立机构所受简谐载荷的频率范围值为100～1500 Hz，分别分析偏心滑块、转子、副轴承结合轴向壁面的应力和振幅响应。

3.5 谐响应分析结果

分析偏心滑块轴向壁面应力图8和振幅图9分别随频率变化的响应可得：偏心滑块轴向壁面在六、七阶处固有频率的应力响应大于一、二阶，在频率为1080 Hz时，应力达到峰值1.15 MPa；偏心滑块轴向壁面在高阶固有频率的振幅变化相比于低阶处的振幅变化大，当频率为1080 Hz时，达到最大振幅为3.8×10-4mm。

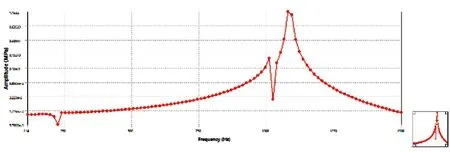
图8 偏心滑块轴向壁面应力响应图

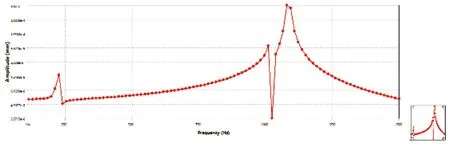
图9 偏心滑块轴向壁面振幅响应图

分析转子轴向壁面应力随频率变化的响应图10可得：转子在六、七阶固有频率处应力响应较大，在频率为1100 Hz左右时，应力达到峰值0.017 MPa。分析转子轴向壁面振幅随频率变化的响应图11可知，转子高阶固有频率处的振幅相比偏心滑块处小，频率在1080 Hz时达到最大振幅为1.75×10-4mm。

图10 转子轴向壁面应力响应图

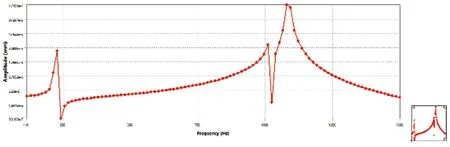
图11 转子轴向壁面振幅响应图

分析副轴承轴向壁面应力图12和振幅图13随频率变化的响应可得：轴承结合轴向壁面在六、七阶固有频率处应力响应大，当频率达到1100 Hz左右时，应力响应达到峰值0.33 MPa；轴承结合面在高阶固有频率处振幅较大但小于转子轴向壁面的振幅，最大振幅出现在频率1100 Hz左右，最大振幅为7.36×10-5mm。

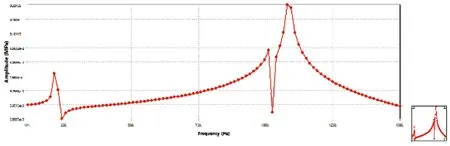
图12 副轴承结合轴向壁面应力响应图

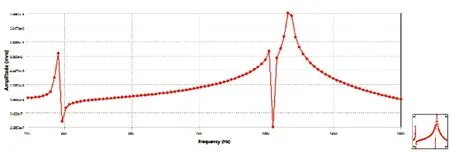
图13 副轴承结合轴向壁面振幅响应图

综上，整个响应分析结果在六阶频率左右达到峰值，更高频率处会逐渐下降，偏心滑块相比于转子和副轴承的响应值更大，所以径向随变机构的可靠性偏心滑块应为重点考虑对象。

4 结论

(1)在径向随变机构中，不同防自转采用不同的限位方法可以确保涡旋压缩机高效运行。通过模态分析获取的振型和固有频率确定了径向随变机构转子系的单薄环节。

(2)稳态简谐响应分析得出机构构件偏心滑块即主轴曲柄销部位应力、振幅响应较大，响应结果对整个转子系统的影响在合理范围内。