一种基于质量因子的多波束测深声呐多子阵相位检测方法

陈世进 吴永清 薛 勐 林晓波 郝程鹏

（1.中国科学院声学研究所水下航行器实验室，北京 100190；2.中国科学院大学，北京 100049）

1 引言

多波束测深声呐利用相互垂直的发射和接收阵列结构和波束形成技术能够在垂直航迹方向上通过一次探测获得数百个测深点，具有较高的测深效率，已经广泛应用于海洋工程测量、海底资源与环境调查以及海底目标勘测等领域［1-4］。多波束测深声呐的测量效率由条带覆盖宽度决定，它描述了水平探测距离与垂直深度之比，是多波束测深声呐最重要的技术指标之一［5］。限制条带覆盖宽度的一个主要因素是多波束测深声呐的边缘波束检测能力［6］。通常来说，镜像波束内的海底回波由于传播损失较小、掠射角较大，因此回波信噪比（Signal-to-Noise Ratio，SNR）较高，使用幅度类检测方法如特征参量相关检测法、快速能量中心收敛法和加权时间平均法等可以获得良好的底检测结果。但是对于边缘波束范围内的海底，由于传播损失较大、掠射角较小导致回波信噪比较低，此时幅度类检测方法的底检测误差较大［7-9］。

为了提高多波束测深声呐的边缘波束检测能力，相关学者相继提出了波束模式拟合类方法和相位检测类方法［10-11］。方位偏差指示法（Bearing Deviation Indicator，BDI）是一种常用的波束模式拟合方法。BDI方法对不同时间片的波束数据进行波束模式的主瓣拟合获取多组角度-幅度命中，通过对某个波束附近的命中进行筛选，并对角度和时间进行加权平均获得该波束的波达时间和波达方向估计。该方法能够在一定程度上提升边缘波束的测深精度。相位检测类方法则通过估计子阵相位差序列的过零点时刻实现波达时间估计，在边缘波束上获得了比幅度类检测方法更高的测深精度。文献［12］将接收阵列划分为两个子阵，利用15个方向的波束数据进行底检测，提升了计算效率，获得了高分辨检测结果，但是两个子阵未能有效利用所有接收阵元，存在阵增益损失。文献［13］将接收阵列划分为多个子阵，提高了阵元利用率，并通过图像变换将相位数据映射为海底图像，提高了浅水环境底检测性能。文献［14］提出MSB-RMU 算法，通过对多个子阵的协方差矩阵进行空间平滑提高了波束方向附近信号的信噪比，同时抑制了其他方向信号，能够兼顾镜像波束和边缘波束的检测效果。

在相位检测过程中，相位模糊会对过零点检测产生干扰。文献［15］推导了两子阵间不存在相位模糊的条件，根据该条件对子阵进行划分从而避免相位模糊的产生。但该方法需要较长的子阵阵长和较短的子阵间距，子阵之间存在大量相互重叠的阵元，在信噪比较低时子阵重叠会使相位差估计量存在较大偏差影响底检测精度。文献［16］介绍了Vernier 方法解模糊原理，但该方法对噪声敏感性较强，容易出现错误的解模糊结果。因此如何在保证相位差估计为无偏估计的前提下对相位差序列准确解模糊，同时选取误差较小的数据进行过零点检测是提升多波束测深声呐边缘波束检测精度的关键。

本文综合考虑阵元利用率和解模糊效率对子阵阵长和子阵间距进行设计，并以质量因子［8］（Quality Factor，QF）为评价准则提出一种基于递推最小二乘的相位差序列提取方法。首先设计一种子阵之间不存在阵元重叠的多子阵结构，利用多个子阵计算不同波束的相位差序列；其次通过多个具有不同间距的子阵降低Vernier 方法对噪声的敏感性，提高解模糊精度；最后以质量因子为准则利用递推最小二乘方法选取信噪比较高的相位差数据进行过零点检测。仿真和实验数据验证了所提方法在边缘波束能够获得良好的底检测性能。

2 多波束测深声呐

2.1 多子阵相位检测原理

考虑一个接收阵列为N元等间距直线阵的多波束测深声呐，如图1所示。假设各阵元全向接收，1 号阵元为参考阵元，阵元间距为d，阵列垂直倾角为ψ，t时刻海底反向散射声波的角度为θ(t)。第i个阵元接收到的信号可表示为

图1 多波束测深声呐接收阵列坐标系统示意图Fig.1 The schematic diagram of a multi-beam echo sounder receiving array

其中，λ为声波波长，v(t)为海底反向散射信号，ni(t)为第i个阵元接收的环境噪声［17］。

分裂子阵相位检测法将接收阵列划分为A，B两个子阵，如图2所示。

图2 分裂子阵示意图Fig.2 The schematic diagram of a splitting subarray

两子阵长度相等，子阵中的阵元个数相等均为L，子阵间距为D个阵元间隔。两子阵接收信号可分别表示为

其中，aA[θ(t)]，aB[θ(t)]∈CN×1分别为子阵A 和子阵B 的导向向量，nA(t)和nB(t)分别为对应的噪声向量。假设每个阵元的噪声均为0 均值，方差的随机变量，并且不同阵元上的噪声相互独立。分别对两子阵在角度θ0方向进行波束形成可得

其中，α(t)=|B[θ0，θ(t)]|2，为t时刻回波功率，ρAB=。注意到，α(t)和ρAB均为实数，因此对式（6）求相位可得角度θ0方向的相位差曲线

为避免相位差曲线偏差引起的底检测误差，需要避免两子阵之间的阵元重叠。考虑将多波束声呐的接收阵列均匀划分为K个子阵，子阵阵元个数L=N/K，如图3所示。

图3 多子阵划分示意图Fig.3 The schematic diagram illustrating the subdivision of a multiple subarrays

对各子阵分别进行波束形成，选取间隔为2Ld的两子阵构成子阵对，并计算相位差序列。第k和k+2个子阵得到的相位差曲线的均值为

其中，angle(⋅)表示求相位操作。从式（8）可知，按照上述方式进行子阵划分得到的相位差曲线为理论相位差曲线的无偏估计。通过对多个子阵对的相位差曲线进行统计平均可得

信噪比与相位差标准差之间的关系可表示为［6］

其中SNRo为子阵输出信噪比。SNRo为子阵输入信噪比SNR和子阵增益G的乘积，即SNRo=SNR×G。对于等间距直线阵子阵增益等于子阵阵元个数L，因此可将式（10）改写为

考虑到多个子阵对能够实现对相位差独立观测，因此利用多子阵方法得到的相位差标准差为

对比式（11）和式（12）可知，使用多个相互不重叠的子阵时，子阵阵元数变少会导致单个子阵的空间增益下降，但是可以通过对多个子阵对观测得到的相位差取平均的方式对增益进行弥补。使用双子阵无重叠的划分方式时，子阵增益最大为N/2，此时相位差标准差为；使用多子阵无重叠划分方式时，根据式（12）可知子阵个数K大于4即可保证相位差标准差小于双子阵无重叠划分。

2.2 多子阵解模糊方法

Vernier 方法是一种常用的解模糊方法［18］，其原理是设计两个具有不同子阵间距的子阵对，分别计算两个子阵对之间的相位差序列，利用相位差序列和子阵间距之间的关系求解非模糊相位差序列。由于Vernier方法在解模糊时仅利用了两个子阵对，当信噪比较低，相位差误差较大时会出现解模糊错误的情况。为降低噪声对相位差解模糊的影响，本文将Vernier方法扩展至多个子阵对情况。

在考虑相位模糊时，第i个子阵对的相位差序列可表示为

其中，Did分别为第i个子阵对的子阵间距，mi为对应的相位模糊数。利用N个子阵对解模糊相当于求解使N个子阵对之间相位差误差最小化的相位模糊数，可描述为如下优化问题

其中m=[m1m2…mN]T。m的每个元素均包含在一个有限整数集内，因此式（14）的一种直接求解方式是遍历m的取值。从式（14）可知，Di的取值会直接影响解模糊性能。文献［11］利用解模糊效率量化了Di对解模糊性能的影响，将解模糊效率推广至多子阵对情况可得

ηN-1越大解模糊性能越好，因此可通过最大化解模糊效率优化子阵间距

其中D=[D1，D2，…，DN]T。考虑到D中元素均约束在一个有限整数集内，通常情况下可先确定D1，然后遍历Di所有的可能取值，获得最优子阵间距D。

3 相位差序列提取方法

对相位差曲线进行解模糊后可以获得一段持续时间较长的连续相位差序列。但是受到波束形成主瓣和旁瓣影响，不同时刻的相位差具有不同的信噪比。在相位差曲线拟合过程中，应当选取具有较高信噪比的相位差曲线进行拟合以保证过零点检测的精度。本节首先介绍质量因子，随后以质量因子为准则通过一种迭代方法选取能够使质量因子最小化的相位差序列，最后进行相位差曲线拟合实现过零点检测。

3.1 相位检测质量因子

相位检测的质量因子可表示为［8］

其中，tD表示波达时间，fθ0(t)为波束方向θ0上的相位差序列，f'θ0(tD)为fθ0(t)在tD处的导数，δΔφ(tD，θ0)为相位差序列在tD处的标准差。

解模糊之后的相位差序列通常呈现非线性特性，因此本文采用二阶多项式对相位差曲线进行拟合。相位差曲线可表示为如下形式

其中，Δφ∈RK×1为K个待拟合相位差数据组成的向量，A=[t2，t，1]∈RK×3，t=[t1，t2，…，tK]T为Δφ中不同元素对应采样时刻组成的向量，α∈R3×1为二阶多项式的系数向量，n∈RK×1为噪声向量。

α的最小二乘解可表示为［19］

根据式（19）可将拟合曲线表示为

其中tf=[t2t1]T。令即可得到θ0方向上的波达时间估计。

3.2 相位差序列选取方法

为避免低信噪比的相位差数据导致底检测误差增加，在曲线拟合时需要对相位差数据进行选择。本文以相位检测质量因子为评价准则提出一种相位差序列选取方法。考虑选取使相位检测质量因子最大化的相位差序列为待拟合的相位差序列，则该问题可描述为如下形式

其中，T 为所有采样时刻构成集合的任一子集，tT，D、和δΔφ(tT，D，θ0)分别为使用T 内采样时刻对应的相位差序列拟合得到的结果。直接对式（21）求解比较困难。通常来说，多波束测深声呐会在一个跟踪窗内进行底检测，因此可以将T内的元素约束在跟踪窗内的采样时刻。接着将解模糊相位差序列过零点作为初始位置，采用一种启发式迭代方法对跟踪窗内的相位差序列进行搜索，每增加一个数据点，判断质量因子是否下降，若下降则丢弃该数据点，否则保留数据点，直至遍历跟踪窗内所有数据得到T。该方法具体流程如下：

（1）首先对解模糊相位差序列过零点附近K个相位差数据进行二阶多项式拟合，K通常设置为10倍脉宽内的采样点数。采样时刻构成的集合记为T0={t1，t2，…，tK}，相位差数据组成的向量记为Δφ0=[Δφ(t1，θ0)，Δφ(t2，θ0)，…，Δφ(tK，θ0)]T。利用T0和Δφ0计算初始化拟合结果αLS，0，过零点时刻和对应的质量因子QF0。

（2）构造第i次迭代所需的相位差向量Δφi=和集合Ti={Ti，tK+i}。利用Ti和Δφi更新αLS，i和QFi。

（3）若QFi＜QFi-1，令Ti=Ti-1，Δφi=Δφi-1，，QFi=QFi-1。

（4）返回第（2）步，直至跟踪窗内数据迭代完毕，输出Ti和QFi。

上述方法每进行一次迭代均需重新计算αLS，该过程存在矩阵求逆运算，当跟踪窗内数据较多时所需计算量较大，不利于多波束声呐对数据进行实时处理。为了降低计算量，考虑使用递归最小二乘方法迭代求解αLS。第i次迭代的最小二乘解为

将式（23）带入式（22）可得

4 仿真分析

本节通过仿真实验验证所提方法的有效性。考虑一个发射基阵条带覆盖宽度为8倍水深，接收基阵按照半波长布阵，阵元数为64的多波束测深声呐。声呐发射CW 信号，频率为300 kHz，脉冲宽度为50 μs，接收机进行带通采样，采样频率为37.5 kHz。假设接收基阵各阵元全向接收，基阵垂直倾角ψ=90°（即接收基阵水平），海底平坦，声呐距离海底垂直深度H=10 m，声呐探测示意图如图4 所示。多波束声呐镜像回波带内信噪比设置为16 dB，按照上述参数仿真回波数据，并对回波数据进行波束形成，波束角度范围为-60°到60°，每间隔1°形成一个波束，共得到121个波束。

4.1 子阵划分及相位差曲线分析

在声呐参数固定情况下，综合考虑基线解相干［7］和子阵间距对相位检测结果的影响对子阵进行划分。某个波束角度θ0上瞬时脚印范围Δx=cT/(2sinθ0)，当子阵间距大于该范围，同一时刻两子阵接收回波几乎不相干，此时相位检测性能较差，因此在子阵划分时应使子阵间距小于Δx。根据子阵间距与相位检测误差的关系可知，在保证子阵回波相干性的条件下，子阵间距越大相位检测误差越小［11］。由设置的声呐参数计算可得在波束角度θ0=60°时Δx约为17个阵元间距，考虑到声呐接收阵元数为64 个，因此本文将子阵间距设置为16d。按照图3 的子阵划分方式，每个子阵包含8 个阵元，整个接收阵列被划分为8 个子阵。将8 个子阵划分为6 个子阵对，并计算相位差序列。图5 给出了-50°，-45°和-40°波束方向上的相位差曲线，图中的红色圆圈表示该波束方向上海底回波到达时刻对应的采样点。从图中可以看出海底回波到达时刻的相位差均在0°附近，但是同时也可以看到相位差曲线在±180°附近均出现了相位模糊。

图5 不同波束角度的相位差曲线Fig.5 Phase difference curves for different beam angles

将带内信噪比降低至5 dB，对比本文多子阵划分方式和两子阵无重叠划分方式在波束角度为-40°时的相位差曲线，仿真结果如图6所示。图6（a）为本文多子阵划分方式得到的结果，图6（b）为1号-21号阵元和44 号-64 号阵元组成的两子阵得到的结果，图6（c）为1 号-32 号阵元和33 号-64 号阵元组成的两子阵得到的结果。对比图6（a）和图5（c）可知，信噪比的降低导致相位差曲线波动更大，但是本文所提子阵划分方式在低信噪比条件下仍然能够获得较为连续的相位差曲线。对比图6（a）、（b）和（c）可知，两子阵无重叠划分方式子阵间距较大，受基线解相干影响严重，相位差曲线过零点与实际海底回波到达时刻差异较大，因此该划分方式的相位检测性能远差于本文所提子阵划分方式。

图6 不同子阵划分方式的相位差曲线对比Fig.6 Comparison of phase difference curves of different subarray partitioning methods

4.2 多子阵相位差解模糊

在D1=16时，根据解模糊效率η随子阵间距的变化关系将子阵间距分别设置为D2=13，D3=11和D4=9。图7（a）～（c）分别给出了使用D1和D2（两个子阵对），D1、D2和D3（三个子阵对）以及D1、D2、D3和D4（四个子阵对）在-50°方向相位差解模糊的结果。从图7（a）中可以看到采样点在620～850 之间有良好的解模糊效果，相位差曲线在此范围内比较平滑。从图7（b）和（c）可以看出，使用三个子阵对的有效解模糊采样点在615～940 之间，比两子阵对多了95个采样点，使用四个子阵对的有效解模糊采样点在610～1020 之间，比三个子阵多了85 个采样点。从上述结果可知，随着子阵对增加，相位差曲线的解模糊范围和解模糊准确程度均有所增加。图8给出了解模糊相位差曲线与理论相位差曲线的对比结果。从图中可以看出正确解模糊的相位差数据与理论曲线吻合的较好，尤其是在相位差过零点附近，解模糊相位差曲线与理论曲线基本一致。该结果也说明本文采用的多子阵检测结构获取得相位差为无偏估计。但是随着采样点增加，解模糊相位差曲线与理论曲线之间误差增大，这是回波信噪比较低导致的，在进行相位差曲线拟合时应该去除这些误差较大的点以提高过零点检测精度。

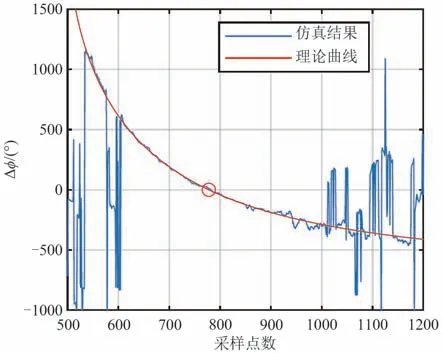
图8 仿真相位差曲线与理论曲线对比Fig.8 The comparison between simulated phase difference curves and theoretical curves

4.3 底检测性能分析

利用本文所提方法从解模糊后的相位差曲线中选取相位差数据进行过零点检测。图9 给出了-50°，-45°和-40°波束方向上相位差序列选取结果，图中红色点标记了选出的相位差数据，黑色点为跟踪窗位置。从图中可以看出该方法选择的相位差数据整体上分布在过零点附近。由于仿真中设置的海底为平坦海底，理论相位差曲线为一段光滑的曲线（如图8 所示），仿真曲线中的波动是受噪声影响产生的，曲线的波动越大说明信噪比越低，反之说明信噪比越高。从图9 中可以看出，提取出的相位差曲线是整个相位差曲线中比较平滑的部分，说明本文所提方法可以有效提取出信噪比较高的相位差数据。

图9 不同角度相位差序列选取结果Fig.9 Results of phase difference sequence selection at different beam angles

对提取出的相位差曲线进行拟合并进行过零点检测，得到底检测结果如图10（a）所示。同时给出BDI 方法的底检测结果作为对比，如图10（b）所示。对比两种方法的底检测结果可以看出BDI方法的检测点容易集中在回波能量较强的位置，在角度上分布不均匀，并且边缘波束容易受波束旁瓣影响产生“隧道效应”。本文方法检测结果在角度上呈现均匀分布，在边缘波束获得了优于BDI 的检测结果，并且该方法未受波束旁瓣影响，在边缘波束能够有效抑制“隧道效应”。

图10 本文方法和BDI结果对比Fig.10 The comparison between proposed method and BDI

图11 通过5000 次蒙特卡洛仿真给出了本文方法、BDI 方法和分裂波束方法在不同角度下的QF 对比。其中分裂波束方法子阵阵元个数为21，子阵间距为43d，该划分方式参考了文献［12］中最优分裂子阵划分方式的结果。为了对比子阵划分方式对检测结果的影响，仿真中增加子阵阵元个数为16 的划分方式，即将阵列均匀划分为4 个子阵。从仿真结果可知，上述几种方法在边缘波束范围内QF 较高，适合用于边缘波束的底检测，同时注意到当波束角度绝对值大于40°时QF 开始减小，这是掠射角的减小和声传播距离的增加导致的。对比本文方法、BDI 方法和分裂波束方法可以看出本文方法在各个波束角度上均获得了最高的QF，说明本文方法整体上性能优于其余两种方法。对比本文方法的两种子阵划分结果可以看出，子阵阵元个数为8 时的QF 高于子阵阵元个数为16 时的QF，这是因为子阵阵元个数为16 时虽然得到了更大的子阵间距，但是损失了两子阵间回波相干性。

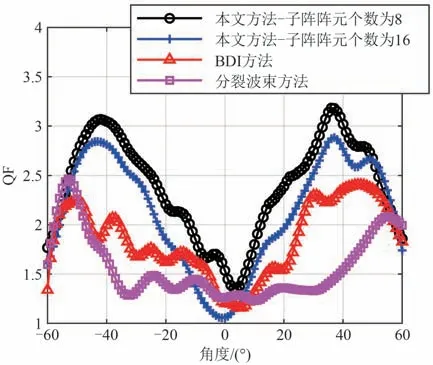
图11 各方法在不同角度下QF对比Fig.11 QF comparison of different methods at different angles

图12 通过5000 次蒙特卡洛仿真对比了波束角度为45°时各方法QF 随信噪比的变化。从仿真结果可以看出各方法的QF 均随信噪比的降低而降低，本文方法仍然在各信噪比下均获得了最高的QF，进一步说明本文方法在各种信噪比条件下性能均优于BDI 方法和分裂波束方法。此外，值得注意的是分裂波束方法的QF 一直都维持在较低的数值，并且随信噪比降低不明显。这可能是由于分裂波束的两子阵间距过大，受基线解相干影响严重，导致该方法QF对信噪比不敏感。

图12 各方法在不同SNR下QF对比Fig.12 QF comparison of different methods at different SNR

5 实验数据处理

为进一步验证本文所提方法性能，对湖试实验数据进行处理和分析。实验中的声呐参数与仿真设置参数一致。图13（a）给出了波束数据结果，从图中可以看出湖底深度在8.5 m左右，镜像回波强度很高同时产生了较强的旁瓣干扰。图13（b）和（c）分别给出了本文方法（子阵阵元数为8）和BDI 方法的检测结果。从图13（b）中可以看出本文方法在边缘波束检测结果较为平滑，测深点基本位于波束主瓣的中心，未受旁瓣泄露的影响。BDI 方法在边缘波束的检测结果波动较大，并且这些波动并非地形变化导致的，从图13（c）中可以看出垂直航迹向距离为6.4 m 和11 m 附近时均因旁瓣干扰产生了错检，本文方法在这些位置则能够有效抑制旁瓣干扰。实验数据处理结果表明本文方法能够在边缘波束获得更优的检测能力。

图13 波束数据及检测结果对比Fig.13 Beamforming data and comparison between detection results

6 结论

本文聚焦多波束测深声呐在相位检测中难以选择合适的相位差数据进行过零点检测的问题，分析了子阵划分对多子阵检测的影响，提出一种基于迭代最小二乘的相位差序列自动提取方法，并通过仿真和实验数据对所提方法进行分析和验证。结果表明：通过合理划分子阵并利用多个子阵对解模糊能够去除由相位模糊导致的过零点干扰，为后续处理提供高质量相位差数据；所提方法以质量因子为评价准则能够从解模糊后的相位差曲线中有效提取出信噪比较高的数据进行过零点检测；相较于BDI方法和分裂波束方法，本文所提算法在边缘波束获得了更高的质量因子，同时具有良好的抗旁瓣干扰能力。实验数据处理结果进一步验证了本文所提算法能够提升多波束测深声呐对边缘波束的检测能力，具备较强的工程应用价值。