一种约束鲁棒加权最小二乘静默定位算法

杨月怡 鄢社锋 李 璇 毛琳琳

（1.中国科学院声学研究所，北京 100190；2.中国科学院大学，北京 100049）

1 引言

随着海洋战略地位的提升和水声技术的发展，水下定位技术引起了越来越多的关注，并在环境观测、搜救捕捞等方面发挥了重要作用［1-4］。以北斗、GPS 为代表的陆地导航定位系统发展较为成熟，但目前适用于水下传感网络的定位方案仍相对较少，水下定位成为近年来的热门研究课题［5-8］。

为获取准确的定位信息，现有的定位算法大多需要各传感节点间保持严格的时钟同步，但水下时钟同步对软件和硬件都提出了极高的要求。2008年，Cheng 等人首次提出水下静默定位算法（Underwater Positioning Scheme，UPS）［9］，该方法无须待定位节点主动通信且免时钟同步，仅需四个参考节点即可构造定位方程组，十分适合注重节能的水下传感网络中的定位。然而定位方程的解算并不十分简单，在参考节点布放阵型不佳时，容易产生较大的定位误差。一般对定位方程的求解有迭代法和解析法。文献［10］在TDOA/AOA 定位中提出一种基于泰勒展开的迭代约束加权最小二乘，有效降低了噪声的影响，提高了定位精度。文献［11］通过引入中间变量将方程转化为约束加权最小二乘估计问题，然后根据牛顿迭代法求解问题。迭代法需要进行多次迭代计算，复杂度高，且对初值的选择和步长敏感，还可能会面临收敛问题。解析法因其不存在不收敛的问题，也被研究学者们广泛关注。文献［12］将定位问题转换为二次规划问题，首先通过拉格朗日法求解方程，然后进一步在约束条件下进行泰勒展开以优化解析解。文献［13］提出一种利用时频差联合定位水下运动目标的方法，该方法使用两步加权最小二乘估计目标节点位置，首先求出运动节点位置、速度的初始估计值，然后对中间变量进行泰勒展开，并带回第一步中以消除忽略二次噪声带来的误差，修正初始估计值。上述算法在观测误差有限的情况下可以达到较高的定位精度，但在复杂的水下环境中容易受噪声干扰导致定位精度严重下降，且算法复杂度较高。为在有限观测量的情况下提高定位精度，本文提出一种结合卡尔曼滤波的约束稳健加权最小二乘算法。该方法首先将定位方程组进行伪线性化，然后引入辅助变量并利用其与待求变量之间的关系对方程进行约束进而求出目标节点的位置估计值。在对目标节点的动态定位中，通过对定位结果的卡尔曼滤波进一步消除定位误差，提高定位精度。仿真及海试数据处理结果表明，本文所提算法可有效提高定位精度。

2 静默定位模型

假设水下三维空间中分布着4个已知自身位置的参考节点，第i个参考节点Bi的坐标为[xi，yi，zi]T，i=1，2，3，4，并将第一个参考节点设为主参考节点。待定位的目标节点S坐标为[x，y，z]T。UPS 算法首先需计算各节点之间的距离，令

水下静默定位算法过程如下：首先，主参考节点B1每隔T秒周期性广播定位信号，发送信号中包括参考节点自身位置和时钟信息等。在n1时刻，待定位节点S接收到来自参考节点B1广播的信标信号。在参考节点B2接收到来自参考节点B1的信标信号一段时间Δ2后，开始广播其信标信号，除自身位置信息外，还包含处理时间Δ2，待定位节点S在n2时刻接收到来自参考节点B2的信标信号。同样，节点B3、B4在收到来自B1的信标信号后开始广播包含其位置信息和处理时间的信标信号。待定位节点S分别在时刻n3、n4接收到来自信标节点B3、B4的信标信号。定位过程如图1 所示。令v为水下声速，Δni=ni-n1，i=2，3，4 为目标节点本地时钟记录的定位信号到达时间差。由此，可得到距离方程：

图1 UPS算法过程Fig.1 UPS positioning process

对方程进行简化：

由上述公式可得：待定位节点仅利用自身时钟记录各定位信号达到时间即可获得参考节点与自身的距离。利用图2的几何关系即可得到待定位目标的位置求解方程组：

图2 几何定位模型Fig.2 Geometric positioning model

UPS 算法采用降阶法求解上述方程，通过简单的数学计算即可得到目标位置的解析解。这种解法无须迭代，计算复杂度低，但定位误差偏大。

本文基于上述静默定位模型，提出一种结合卡尔曼滤波的约束稳健加权最小二乘算法。该算法首先将静默定位问题转化为二次规划问题，然后利用拉格朗日乘子法和广义奇异值分解求出目标节点的坐标。

3 基于静默定位模型的算法改进

3.1 约束稳健加权最小二乘定位算法

在实际应用中，待定位节点的深度信息可由压力计等其他外部设备得到，作为已知信息。此时，可将非线性方程组转化为伪线性方程组，并利用最小二乘（Least Square，LS）方法进行求解。具体来说，将式（5）整理为伪线性方程组：

LS 算法中假设X中的变量x，y，d1s是相互独立的，然而目标节点与参考节点B1的距离d1s为辅助变量且存在。因此，利用这一相关性，本节提出一种约束稳健加权最小二乘（Constrained robust weighted least square，CRWLS）算法，对定位结果进行改进。将静默定位问题转化为线性约束最优化问题，则可以构建目标函数：

即将静默定位问题转换为带有二次约束的二次规划问题。式中Xa=[x1，y1，0]T，Σ=diag(1，1，-1)，c=-(z-z1)2，W为加权矩阵。当W为单位阵时，各观测量权值相同。

利用拉格朗日乘子法求解上述方程，即：

式中λ为拉格朗日乘子。对式（8）中X求导并令其为0，可得：

将式（9）代回约束条件可得拉格朗日乘子λ的解。然后利用广义奇异值分解（Generalized singular value decomposition，GSVD）的方法将ATW-1AΣ对角化为：

式中Λ=diag(ζ1，ζ2，ζ3)为对角矩阵，因此式（8）可重新写作：

式中p=[p1，p2，p3]T=UTΣ(ATW-1b-ATW-1AXa)，q=[q1，q2，q3]T=U-1(ATW-1b-ATW-1AXa)。可通过卷积计算简化式（11），并对多项式进行求根运算，考虑到实际意义，仅保留方程的实数根。并将实数解依次带入式（9）得到对应的估计值，再将带入目标函数J(X)，找到使目标函数最小的X即为最优解。

当各观测量中的噪声都为高斯分布时，CRWLS算法中的权值矩阵取单位阵即可得到较为准确的目标节点位置估计值。然而由于水下声速分布的非均匀性，声波在水下并非沿直线传播，在不对声线弯曲进行修正的情况下，若仅采用固定声速来计算水声信号的传播距离将产生较大误差［14］。本节通过稳健加权方法，根据残差赋予各观测量权值。权函数在平差过程中计算残差，残差越大，认为其可信度越低，所对应的权函数越小，经过多次迭代可使残差小的观测量占比更大，减少噪声对定位精度的影响。构建残差方程为：

求解上式可得残差V的估计值，并以此构建权值矩阵W，并带回方程，迭代更新。常见的等价权函数有Huber 权函数、IGG3 权函数、Tukey 权函数等［15］，不论形式如何变化，权函数总在平差过程中随残差改变，实际应用时可根据实际情况选取，本节选择IGG3权函数，其权重因子为：

通常k0取值为1～1.5，k1取3。式中，|分别为系数矩阵与第i个观测量的残差为权值因子。等价权函数随残差的增大而减小，对噪声较大的观测数据进行降权处理，从而减小了观测信息中的噪声对定位精度的影响。

根据上述公式，最终得到约束稳健加权最小二乘算法迭代求解步骤如表1所示。

表1 约束稳健加权最小二乘算法流程Tab.1 Constrained robust weighted least squares algorithm flow

3.2 卡尔曼滤波算法

水下定位系统中，观测量的精度决定了系统的定位精度。然而由于水下复杂的物理环境，观测量往往受到各种噪声的影响，从而存在一定误差［16］。当待定位节点处于运动状态中时，卡尔曼滤波算法因其可以利用更多测量信息，相比每时刻独立定位能够获得更好的定位估计精度。因此，为进一步提高定位精度，可利用运动状态的连续性，进一步扩展UPS 定位算法，使用卡尔曼滤波对定位结果进行预测，提高定位精度。

利用k时刻UPS 解算的定位结果构造k时刻的状态向量为X(k)=[xk，yk，vk，vy]T，分别为k时刻目标节点在x方向、y方向上的坐标和速度，然后建立状态方程和观测方程：

式中F为状态转移矩阵；Z(k)=[xk，yk]T为k时刻观测量；M(k)为系统噪声；H为观测矩阵；V(k)为观测噪声。其中，M(k)和V(k)是互不相关的零均值高斯分布序列，其协方差矩阵分别为Q(k)、R(k)。假设目标节点做匀速直线运动，将速度的变化视为水体的扰动，则：

由式（14）可得状态向量X(k)的进一步预测和k时刻的预测误差协方差矩阵为：

利用上一节中提出的算法得到目标节点位置信息后，可更新观测值Z(k)。此时k时刻状态变量的估计可由上一时刻的预测值和观测量Z(k)联合表示为：

其对应的协方差矩阵为：

其中，K(k)为卡尔曼滤波增益：

4 仿真分析

为了验证文章所提算法的有效性和可靠性首先进行仿真实验。为模拟水下环境，在仿真实验中以Munk 声速剖面为背景，利用射线声学原理模拟声波在水下的传播轨迹，进而求出声波的传播时间，并进行后续实验。实验中设置四个参考节点，按矩形设置基阵位置，参考节点位置分布如表2所示。

表2 参考节点布放参数Tab.2 Reference node layout parameters

4.1 测时误差影响分析

UPS定位算法在本地记录来自各个参考节点定位信号的到达时间，并以此计算出各参考节点与目标节点之间的距离，从而得到目标节点的位置估计。这种方法免去了时钟同步从而不存在时钟差误差［17］，但声波在水下的传播会发生能量衰减，使定位信号被淹没在噪声中，同时多径效应、水面反射、多普勒效应［18］等仍会影响测时准确性。为分析测时误差的影响，假设测时误差为高斯分布，误差范围0～4 ms，参考节点坐标如表2所示，目标节点位置选择接近阵中心处，坐标为[1500，1500，100]T。进行1000 次蒙特卡洛仿真实验，并用均方根误差RMSE评估，如式（22）。

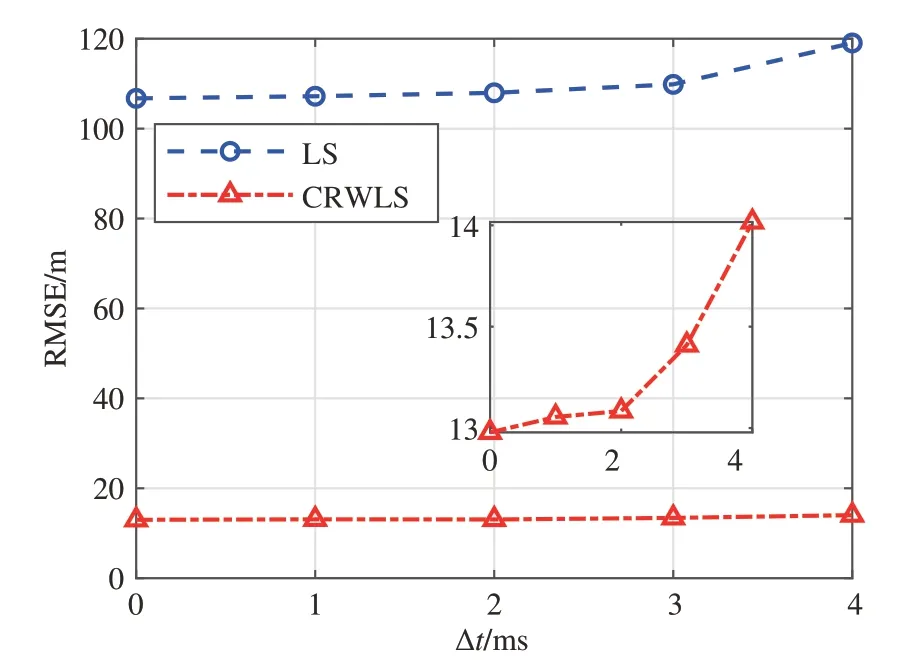
图3 不同测时误差时的定位结果均方根误差Fig.3 RMSE under different delay measurement errors

4.2 声速误差影响分析

水下声速是UPS 算法中的基本参量之一，UPS中距离信息是由时延差和声速的乘积获取，故声速的变化很大程度上会影响UPS 定位精度。由于海水的分层特性，水下存在声速弯曲问题，通常认为海水中的平均声速约等于1500 m/s。在不能获取水下声速剖面的情况下，等效声速的设置将直接影响UPS定位的准确性。为分析不同声速下UPS算法的定位误差，将等效声速分别在1489 m/s～1519 m/s 处取值，节点位置与上述实验相同，并用均方根误差RMSE 评估定位性能。图4 给出了在不同等效声速下，经典LS算法和本文CRWLS算法的均方误差，可以看到，在等效声速设置的较为合适时，LS 算法与CRWLS算法估计误差相近，但在等效声速估计误差较大的情况下，LS 算法定位误差迅速增加，导致算法失效，而CRWLS 算法的定位误差增长速度明显小于LS 算法，相比之下更为稳健。这是因为LS 算法在对目标节点进行定位时将目标节点位置与辅助变量视为相互独立的变量，从而对定位方程进行伪线性化，而CRWLS 算法考虑了待求变量中误差的相关性，且稳健权函数可以有效降低观测信息中噪声的影响。

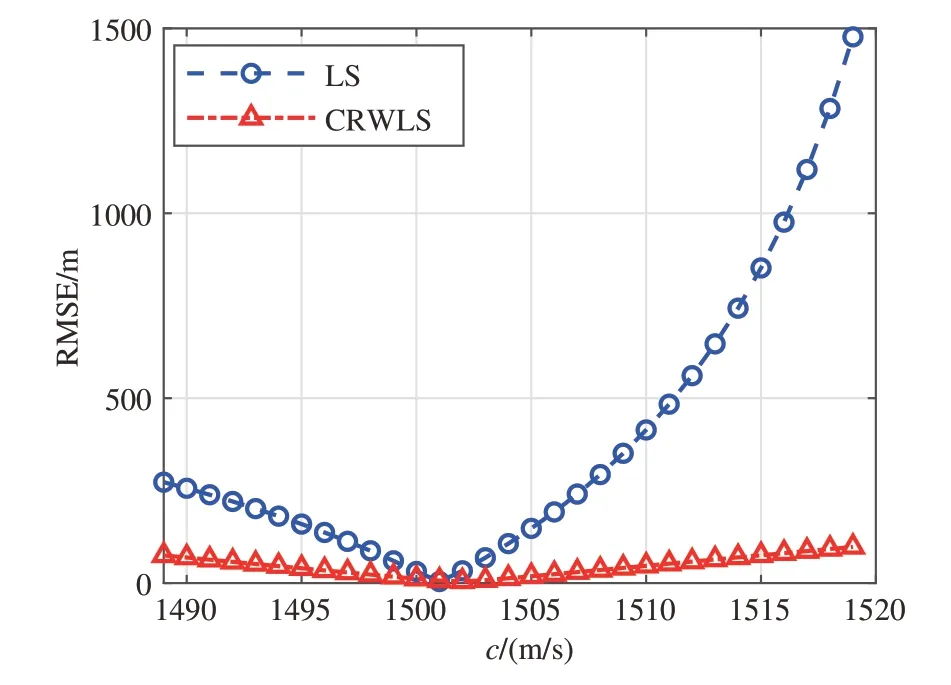
图4 不同声速下的定位结果均方根误差Fig.4 RMSE under different sound velocity

4.3 静态定位误差分析

首先进行静态定位实验，参考节点位置如表3所示，深度保持100 m 不变。图5 给出了LS 算法和CRWLS 算法的定位结果，可以看出本文提出的CRWLS 算法相比于经典LS 算法定位误差更小，尤其在阵的边缘位置处，LS算法得到的位置估计已明显偏移目标节点真实位置，算法失效。仿真实验中LS 算法的估计误差达74.8 m，而本文所提出的CRWLS算法误差为6.5 m，定位误差明显下降。

表3 参考节点布放参数Tab.3 Reference node layout parameters

图5 阵内不同位置处定位结果的均方根误差Fig.5 The RMSE for different position within the array

4.4 动态定位误差分析

进一步地，本节进行水下动态定位实验。UPS算法的观测量中必然存在着一些误差，使用卡尔曼滤波可在一定程度上消除噪声的影响，有效跟踪目标节点的运动。动态定位的仿真实验环境设置与静态定位实验相同。假定目标节点在x方向上移动的速度为1.5 m/s，y方向上移动速度为2 m/s，20 s后转向，保持x方向速度不变，y方向速度降至1.6 m/s，目标节点深度始终保持100 m 不变。根据CRWLS 算法得到目标位置观测值后，利用卡尔曼滤波算法进一步改进定位结果，定位误差如表4所示。可见，卡尔曼滤波进一步减小了定位误差。

表4 卡尔曼滤波前后误差对比Tab.4 Error comparison before and after Kalman filter

5 试验验证

为进一步验证所提算法有效性，利用在青岛胶州湾展开的水下静默定位实验中获取到的数据对所提算法进行验证。考虑到试验的便捷性，令待定位节点与试验母船保持连接，利用10 m长线缆将其吊放入水并在其上方水面处架设GPS 天线，为定位提供位置参考。实际定位时会停船测试，保持GPS和吊放设备相对静止。实验设备如图6所示。

图6 试验中所用设备及节点布放过程Fig.6 Equipments used in sea trial and node deployment process

将定位精度较高的GPS 给出的运动轨迹作为位置参考，将解算出的目标轨迹与GPS 定位轨迹进行对比，对所提出的定位算法进行验证，定位结果如图7所示。图中黑色实线为GPS给出的目标节点运动轨迹，本文将其作为目标节点在水下的实际运动轨迹；红色虚线为经典LS算法估计出的目标节点运动轨迹；蓝色点划线为本文所提出的CRWLS 算法解算出的运动轨迹；紫色点虚线为卡尔曼滤波后的CRWLS 算法。可以看出，由LS 算法解算出的目标节点定位轨迹已明显偏移真实运动轨迹；而本文所提CRWLS 算法得出的目标节点定位轨迹已较为接近GPS 给出的运动轨迹，进一步地，经过卡尔曼滤波后，解出的目标节点运动轨迹更为光滑，定位误差也更小，精度更高。仿真和海试实验都表明本文所提出的约束稳健加权最小二乘算法得到的定位结果更接近目标的实际运动轨迹，而卡尔曼滤波的加入进一步使得定位轨迹更为平滑，更接近实际运动规律。本文所提算法求出的目标节点运动轨迹与真实位置仍存在一定误差，这是由于海水是非均匀介质，声波在水下传播时会发生折射反射现象，而并非沿直线行进。UPS 算法将声波在水下的传播速度设为常数，结合测得的传播时间直接计算出定位信号的传播距离，并未考虑声波在水下的传播特性，因此存在较大的测量误差。要解决这一问题可射线声学原理对定位结果进行修正［19］。

6 结论

针对水下静默定位算法精度较差的问题，本文提出一种结合卡尔曼滤波的约束稳健加权最小二乘算法。该算法将目标节点到参考节点之间的距离作为辅助变量并利用其与目标节点坐标之间的相关性，对方程进行约束。通过引入拉格朗日乘子法和广义奇异值分解，本文给出了目标节点坐标的解析解。通过对观测数据进行稳健加权，对噪声较大的数据进行降权处理，CRWLS算法可有效提高对噪声的鲁棒性，提高静默定位算法的定位精度。在对目标节点进行动态定位时，本文进一步利用卡尔曼滤波对定位结果进行处理以消除噪声的影响。仿真与试验数据处理结果表明，相比于经典最小二乘算法，约束稳健加权最小二乘算法可以获得更加准确且更稳健的定位结果。