一类边界退化的四阶抛物型方程解的存在性

李 彬,马永峰,梁 波

(1.大连交通大学 理学院,辽宁 大连 116028;2.滁州学院 数学与金融学院,安徽 滁州 239000)

0 引言

四阶退化抛物型方程在生物数学、材料科学、工程、图像分析、海洋物理等领域均得到了广泛的应用，而Cahn-Hilliard方程、薄膜方程和半导体方程为代表的四阶方程在这些领域中应用更为广泛。Cahn-Hilliard方程通常是用来描述相变理论。(1)参见J. W. Cahn, J. E. Hilliard, “Free energy of a nonuniform system. i. interfacial free energy”, J. Chem. Phys. no.28, 1958.薄膜模型刻画了一层超薄的粘性可压缩的流体沿倾斜介质的运动过程，方程中的未知解通常代表薄膜的厚度或高度。(2)参见A. Zangwill, “Some causes and a consequence of epitaxial roughening”, Journal of Crystal Growth. no.163, 1996.此外，半导体型模型与四阶退化的抛物方程也具有一定的联系，其中杂化量子漂移—扩散模型和混合量子流体动力学模型可以被认为是四阶抛物方程的边界退化问题。(3)参见F. D. Michele, M. Mei, B. Rubino, R. Sampalmieri, “Thermal equilibrium solution to new model of bipolar hybrid quantum hydrodynamics,” Journal of Differential Equations. no.263, 2017.

梁波、吴晓琴等人研究了一类四阶抛物方程在一维情况下的时间周期解的存在性问题：(4)参见梁波、吴晓琴、张振宇：《一类非线性四阶抛物方程周期解的存在性》,《大连交通大学学报》2018年第5期。

u(x，t+ω)=u(x，t)x∈(0，1)，t∈R，

ux|x=0，1=uxxx|，x=0，1=0，t∈R。

周鸣君、王春朋等人根据退化项xλ退化性的强弱分别研究了一类边界退化的二阶抛物型方程初边值问题解的淬火现象。(5)参见Zhou Mingjun, Wang Chunpeng and Nie, Yuanyuan, “Quenching of solutions to a class of semilinear parabolic equations with boundary degeneracy”, J. Math. Anal. Appl. no.421, 2015.问题如下：

u(x，0)=0，x∈(0，a)。

其中，λ>0，a>0，f∈C2([0，c))(c>0)，且f满足下列条件：

这篇文章证明了在退化性不强的情况下，存在一个临界长度，当空间间隔小于该临界值时，解在时间上全局存在，当空间间隔大于该临界值时，解在有限时间内将会产生淬火现象。

我们考虑将其进行改进得到本文所要讨论的边界退化的四阶抛物型方程：

ωt+(xλωxx)xx-(xλωx)x=g(x，t)，(x，t)∈(0，a)×(0，T)，

(1)

ωx(x，t)|∂Ω=0，ω(x，t)|∂Ω=0，t∈(0，T)，

(2)

ω(x，0)=ω0(x)，x∈(0，a)，

(3)

其中，λ>0，a>0，g(x，t)∈L2((0，a)×(0，t))。

我们发现，比较原则和最大值原理对于高阶偏微分方程是不成立的，因此我们有必要采用一些新的原理、方法或技术。那么，本文将考虑采用能量估计以及渐进极限的讨论来证明该问题解的存在性。

定义 我们称ω=ω(x，t)是问题(1)-(3)在QT=(0，a)×(0，T)上的一个弱解，如果满足下列条件：

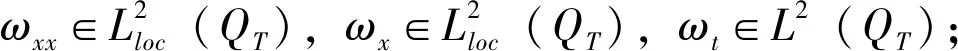
此定理为本文主要结论，下面将利用近似解的估计和渐进极限讨论给出相应的证明。

1 非退化情形下解的存在唯一性

为了研究边界退化问题(1)-(3)，先考虑其正则化问题：

ωζt((xλ+ζ)ωζxx)xx((xλ+ζ)ωζx)x=g(x，t)，(x，t)∈(0，a)×(0，T)，

(4)

ωζx(x，t)|∂Ω=0，ωζ(x，t)|∂Ω=0，t∈(0，T)，

(5)

ωζ(x，0)=ω0ζ(x)，x∈(0，a)，

(6)

其中，ζ>0。

本节，我们将用ωζ表示初边值问题(4)-(6)的解，且假设初始函数ω0ζ→ω0在L2(Ω)中强收敛，它的存在性如下：

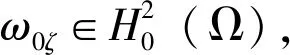
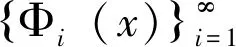
使其满足下面的方程：

(ωζnt，Φk)+(xλωζnxx，Φkxx)+(xλωζnx，Φkx)=(g，Φk)，k=1，2，…，n.

(7)

(8)

在L2(Ω)中强收敛，则问题(7)-(8)解的存在性可以由Peano定理来保证。下面对近似解进行估计。

对其在(0，t)上积分，得：

然后，可以得到：

(9)

其中μ是Poincare不等式中的常数。

(ωζnt，ωζnn)+((xλ+ζ)ωζnxx，ωζntxx)+((xλ+ζ)ωζnx，ωζntx)=(t，ωζnt)

对其在(0，t)上积分，得：

然后，可以得到：

(10)

由(9)-(10)，可以得到如下估计：

(11)

‖ωζnt‖L2(0，T；L2(Ω))≤C。

(12)

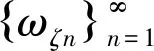
(13)

ωζnt→ωζt在L2(0，T；L2(Ω))中弱收敛。

(14)

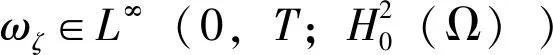
下面，证明解的唯一性。

令ω，υ分别为问题(4)-(6)的两个弱解。由弱解的定义，可以得到：

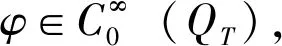
对于任意固定的s∈[0，T]，我们可以选择作χ[0，s](ω-υ)为上述等式中的检验函数，其中χ[0，s]是[0，s]上的检验函数。令Qs=Ω×(0，s)，因此就有：

由此可得：

因此，ω(x，s)=υ(x，s)在QT上几乎处处成立，解的唯一性证明完毕。

2 退化情形下解的存在性

本节的主要内容是建立不依赖于ζ的一致估计以及讨论ζ→∞的极限。其中，一致估计的结果由下面的引理给出。

引理1 逼近解ωζ具有如下的一致估计：

‖ωζ‖L∞(0，T；H1(Ω))≤C；

(15)

‖ωζt‖L2(0，T；L2(Ω))≤C；

(16)

(17)

(18)

其中，C不依赖于ζ。

证明：令χ[0，t](t)为区间[0，t](其中0≤t≤T)上的检验函数，取命题-(ⅱ)中φ=ωζχ[0，t](t)。

于是有：

于是，可以得到：

(19)

其中，μ是Poincare不等式中的常数。

然后，取命题-(ⅱ)中的检验函数为φ=ωζtχ[0，t](t)，于是有：

然后，可以得到：

(20)

由(19)-(20)，可以得到估计(15)-(18)，证毕。

下面证明本文的定理，即证明解在退化情形下的存在性。

根据先验估计(15)-(18)，结合Aubin-Lions紧致性定理可知，存在ω和{ωζ}(不妨仍然记为其本身)使得：

ωζ→ω在L∞(0，T；H1(Ω))中弱收敛；

(21)

ωζt→ωt在L2(0，T；L2(Ω))中弱收敛；

(22)

(23)

(24)

在命题-(ⅱ)中令ζ→∞可得：

所以是问题(1)-(3)在QT上的一个弱解。结合ω∈L∞(0，T；L2(Ω))和ωt∈L∞(0，T；L2(Ω))，应用Aubin引理(6)参见伍卓群、尹景学、王春朋：《椭圆与抛物型方程引论》,北京：科学出版社,2003年。可以得到ω∈C(0，T；L2(Ω))。