磁性光子晶体表面与各向异性轴平行时的透射性能

杨 瑞,段鹏雨,崔海瑛

(大庆师范学院 机电工程学院,黑龙江 大庆 163712)

0 引言

磁性材料在微电子学技术、微波与红外技术上得到广泛应用，这引起了物理学界对磁性材料的物理性质进一步探究的热情。近年来，人们广泛地关注着以磁性材料作为组分的光子晶体的研究。这种磁性光子晶体以其独特的磁光性质而区别于普通电介质光子晶体。(1)参见Ionue M,Fujikawa R,“Baryshev A：et al. Magnetophotonic Crystals”. J. Phys. D： Phys,vol.39,no.2, 2006.人们还利用磁性介质的共振特性，实现了电磁波在磁性光子晶体中存储的功能。(2)参见Lin Z F,Chui S T,“Manipulating Electromagnetic Radiation with Magnetic Photonic Crystals”. Opt. Lett,vol.32,no.16, 2007.磁性光子晶体还具有许多新颖的特性，比如光的单向性、显著的法拉第旋光性等。(3)参见Wang X Z,“The Faraday Effect of an Antiferromagnetic Photonic Crystal with a Defect Layer”. J. Phys., Condens. Matters,vol.17,no.36, 2005.这些研究为调整光子晶体性能提供了更多的途径。科学界对磁性光子晶体的研究正处于发展阶段，因而具有非常广阔的研究空间。

目前，由磁性材料构成的功能器件的响应频段已经扩展到了太赫兹领域，(4)参见范飞、郭展等：《多功能磁光子晶体太赫兹可调偏振控制器件》,《物理学报》2011年第8期。对太赫兹电磁波的研究成为前沿领域的一部分，太赫兹技术的发展引起了世界范围内专家学者的高度重视。由于反铁磁材料的共振频率恰好处在太赫兹频段，我们可以利用反铁磁材料来加工太赫兹信号。因此，对反铁磁体系中太赫兹波传播性质的研究是适时的。(5)参见I. L. Lyubchanskii,N. N. Dadoenkova,et al., “Rasing.Magnetic Photonic Crytals”.J. Phys. D： Appl. Phys,vol.36, 2003.

磁性光子晶体独特的光子带隙结构使其具有优异的光电子学特性。由于一维体系结构简单并且易制备，同时还具备二维和三维体系的主要性质，因此具有非常高的理论研究价值和广泛的应用前景(结构如图1所示)。带结构和电磁波的传输特性是一维磁性光子晶体研究的重点，宋玉玲等人对一维有限厚度的反铁磁光子晶体的带结构和透射性质进行了研究。

(a)一维光子晶体 (b)二维光子晶体 (c)三维光子晶体

王选章针对Faraday位型，研究了电磁波垂直入射到铁磁/非磁性多层膜的透反射性质，又针对Faraday和Voigt位型，研究了反铁磁/电介质多层膜的透反射性质。(6)参见宋玉玲、王选章：《一维受限反铁磁光子晶体的性质》,《光学学报》2008年第12期.随后又研究了电磁波倾斜入射到反铁磁裸膜表面时的非线性的透反射问题。

本文主要研究当各向异性轴与外场均平行于反铁磁体系表面时，有反铁磁缺陷层的一维光子晶体的透反射性质。对反铁磁裸膜光学性质的研究是研究反铁磁光子晶体光学性质的基础，因此，本文从反铁磁裸膜的色散关系的研究入手，设定不同介质中电磁波的波解形式，通过电磁场的边界条件得出传递矩阵，最后给出反铁磁裸膜和带有反铁磁缺陷层的一维光子晶体的透反射率并进行数值模拟，得出最优的结构方案。

1 基本模型及理论计算方法

(1)反铁磁单层膜结构：

图2 反铁磁单层薄膜的位型图Z

根据麦克斯韦方程可以得到反铁磁薄膜中电磁波的磁场强度满足的波动方程为：

(1)

(2)

(3)

(4)

(5)

上式中，磁场强度有非零解的条件是其系数等于零。因而得到电磁波在反铁磁层中的色散关系为：

(6)

根据色散关系，讨论反铁磁体系的透反射性质。反铁磁层中电磁波的磁场强度可以表示为：

Hx=[Aaexp(ikyy)+Baexp(-ikyy)]exp(ikzz)exp(-iωt)

(7)

其中，Aa和Ba分别表示电磁波沿y轴正、负方向传播的振幅。

(8)

为了解决电磁波入射到反铁磁裸膜上的透射问题，需要在裸膜上下表面应用电磁场连续的边界条件，进而得到透射波振幅和入射波振幅之间的传递矩阵，求解出体系的透射率。

设电磁波在反铁磁上部空间和下部空间的磁场强度的表达式分别为：

Hx上=[I0exp(ikty)+rexp(-ikty)]exp(ikzz)exp(-iωt)

(9)

Hx下=texp(ikby)+rexp(ikzz)exp(-iωt)

(10)

(11)

(12)

根据切向场Hx和Ez在薄膜上下表面连续性条件，可以得到从上部空间的电介质到反铁磁层中磁场强度振幅的传输关系为：

(13)

以及从反铁磁层到下部空间电介质中磁场振幅的传输关系为：

(14)

其中，Tta和Tab为相应振幅之间的传输矩阵，具体形式如下：

(15)

(16)

其中，Δta=εtka/εakt，Δab=εakb/εbky，δa=exp(ikyda)。

因此，根据表达式(13)和(14)可以得到从反铁磁裸膜上部空间到下部空间磁场强度振幅之间的传输关系为：

(17)

其中，∏=TtaTab。因此可以求得透射波振幅的表达式为：

t=I0/∏11

(18)

因此，电磁波通过反铁磁单层膜的透射率为

(19)

(2)带有反铁磁缺陷层的一维光子晶体的结构：

图3 带有反铁磁缺陷层的一维光子晶体的结构

电介质层i(i=1，2)中电磁波的磁场强度可以表示为：

Hx=[Aiexp(ikiy)+Biexp(-ikiy)]exp(ikzz)exp(-iωt)

(20)

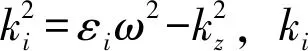
(21)

根据切向场和连续的边界条件，以及各区间相应场的表达式(7)-(12)以及(20)和(21)分别可得：

(a)上半空间到电介质层1中磁场强度振幅的传输关系为：

(22)

式中，为上半空间到电介质层1中磁场强度振幅的传输矩阵，具体形式如下：

(23)

其中，Δt1=εtk1/(ε1kt)。

(b)相邻层之间磁场强度振幅的传输关系为：

(24)

式中，TIJ为层i到相邻的层j中磁场强度振幅的传输矩阵，具体形式如下：

(25)

其中，Δij=εikj/(εjki)，δi=exp(ikidi)，角i，j=1，2，a标分别对应电介质层1、电介质层2和反铁磁层a的相应物理量，且i≠j。

(c)电介质层1到透射介质中磁场强度振幅的传输关系为：

(26)

式中，Ta2为反铁磁层到电介质层2中磁场强度振幅的传输矩阵，具体形式如下：

(24)

式中，TIJ为层i到相邻的层j中磁场强度振幅的传输矩阵，具体形式如下：

(27)

其中，Δ1b=εtkb/(εbkt)。

利用以上这些传输矩阵，可以得到从上半空间经过带有反铁磁缺陷层的一维光子晶体到下半空间磁场强度振幅之间的传输关系为：

(28)

式中，∏可表示成如下形式：

∏=Tt1(T12T21)N/2-1T12T2aTa2(T21T12)N/2-1T21T1b

(29)

2 数值模拟与分析

本文中电介质、反铁磁层材料分别是SiO2、ZnF2、MnF2反铁磁薄膜为例。反铁磁薄膜上下空间的电介质为空气，相对介电常数和磁导率都为1，SiO2、MnF2电介质相对介电常数分别为2.3和8.0。MnF2的厚度为da=255μm，共振频率ωr/2πc=9.7588cm-1，交换场为He=550kG，各向异性场为Ha=7.87kG，子格饱和磁化为M0=0.6kG，旋磁比为γ=1.97×1010rads-1kG-1，阻尼系数为τ=0.001。

图4所示为电磁波在反铁磁单层膜MnF2中和带有反铁磁缺陷层的一维光子晶体(SiO2/ZnF2)4MnF2(ZnF2/SiO2)4的透射率随电磁波频率和入射角变化对比图。由于在反铁磁共振频率附近，反铁磁介质的吸收比较明显，所以图中对于反铁磁单层膜，当电磁波频率位于共振频率附近时，反铁磁体系的透射率迅速降低。而且这个低透射率的频率宽度随着入射角的增大先减少后增加；当入射角为90°时，反铁磁体系的透射率为零。对于带有反铁磁缺陷层的一维光子晶体，随着入射角度的增加，透射谱中的宽禁带向高频方向移动，这是由于入射角度增加使电磁波在各层中光程增加引起的。禁带中存在两个缺陷模，增大入射角时，位于高频的缺陷模的透射率先增大后减小，并向高频方向移动；而位于低频的缺陷模的透射率却一直在减小。

图4 反铁磁单层膜MnF2和(SiO2/ZnF2)4MnF2(ZnF2/SiO2)4结构的透射率随入射角和频率的变化

图5所示为反铁磁单层膜MnF2两侧电介质双层(SiO2/ZnF2)N数量，分别为N=3、4、5时电磁波垂直入射(SiO2/ZnF2)NMnF2(ZnF2/SiO2)N到结构中的透射谱。从图5中可以看到，每个透射谱中均存在很宽的禁带，而且在这个禁带中出现了两个缺陷模，位于反铁磁共振频率附近。当增加光子晶体中电介质双层的数量时，这两个缺陷模的透射强度降低。在N=5时，这两个缺陷模趋于消失。

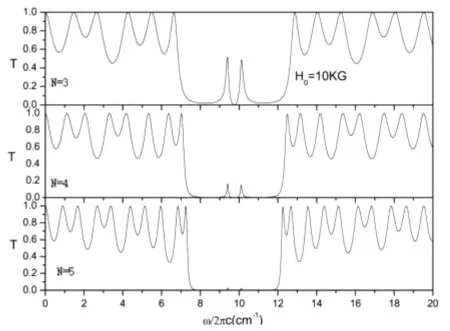
图5 (SiO2/ZnF2)NMnF2(ZnF2/SiO2)N结构的透射谱

图6所示为(SiO2/ZnF2)4MnF2(ZnF2/SiO2)4和(ZnF2/SiO2)4MnF2(SiO2/ZnF2)4两种超晶格结构的透射谱对比图，图中电磁波为垂直入射，两种结构的透射谱中都出现了宽禁带，并处于相同的频率区间，且两种结构出现的缺陷模的频率位置也相同，然而对于(ZnF2/SiO2)4MnF2(SiO2/ZnF2)4结构，缺陷模的透射率非常低，几乎趋近于零。

图6 (SiO2/ZnF2)4MnF2(ZnF2/SiO2)4和(ZnF2/SiO2)4MnF2(SiO2/ZnF2)4两种结构的透射谱

3 结论

本文利用传递矩阵法结合麦克斯韦方程组推导了反铁磁各向异性轴与外场平面平行于反铁磁体系表面时的透射率，并对TM波斜入射到反铁磁裸膜和带有反铁磁缺陷层的一维光子晶体中的透射规律进行数值模拟及性质分析，得到如下结论：

对于反铁磁单层膜，吸收峰出现在共振频率处，吸收峰的频宽随着反铁磁层厚度的增加而增加，随入射角的增加而先减少后增加。对于带有反铁磁缺陷层的一维光子晶体，透射谱中会出现宽光子禁带，禁带中反铁磁共振频率附近存在缺陷模，缺陷模的透射率随体系电介质双层数和层的位置而变化。缺陷模的透射率随着介质层增加降低，电介质层的位置互换，体系透射谱中禁带宽和带中缺陷模的频率位置不受影响，但当层位互换时，介电常数质层1大于层2时，缺陷模的透射率降低明显，且随入射角的增加，高频处缺陷模的局域效果明显减弱。

综上，随着光电功能材料的广泛应用，对新型超晶格结构合理设定反铁磁薄膜厚度、介质层数及电磁波入射角度，都可对光子禁带的带宽进行拓展应用，进而据其特性设计光电功能器件。本文的理论研究对于光开关、光电耦合器的设计和超晶体材料的非线性效应及其功能器件的设计可以提供一定的理论借鉴。