秸秆还田机振动特性分析与试验研究
赵晓顺,冉文静,霍晓静,刘尚坤,于华丽
(河北农业大学 机电工程学院,河北 保定 071001)
农作物秸秆是重要的生物质资源。秸秆还田能够增加土壤有机质、培肥地力、提高作物产量,是实现秸秆有效处理的主要途径之一[1-2]。机械化秸秆还田存在振动剧烈、噪声高现象[3-7]。强烈的振动不仅造成整机可靠性降低且平均无故障作业时间短等问题,也严重影响驾驶员健康及操作舒适性,是制约秸秆还田机可靠性和舒适性发展的主要原因[8]。秸秆还田机是1 个有限多自由度的弹性系统,受激振作用产生振动与变形。其振动的产生主要由共振或轴不对中所造成[9]。当激振频率与秸秆还田机某部件的固有频率相同时,该部件会产生强烈的共振现象,造成机器损坏[10]。
振动问题已成为影响农机可靠性和舒适性的阻碍因素之一。目前,国内外学者对农业机械装备的研究主要集中在模态分析与试验、振动测试分析、减振控制、结构参数优化等方面。徐立章等[11]针对履带式全喂入水稻联合收获机整机振动大的问题,研究了其发动机空载、整机空载和田间收获等5 种工况下的多点振动的时域特性和频谱特性规律,改善了联合机的驾驶舒适性。李耀明、张佳喜等[12-13]通过对农机进行模态试验验证及理论分析,对机架进行结构优化与试验,有效避免了割台产生共振。蒋亚军、舒彩霞等[14-15]针对油菜割晒机振动引起机架大振幅问题,其通过建模研究了自由模态下模态频率和振型,结合模态试验与仿真验证了有限元模型的准确性。马桂香、姚艳春等[16-18]对联合收获机进行振动溯源并研究其振动特性。吕小莲、高文英、薄鸿明等[19-21]对秸秆还田机进行了模态分析。Wout 和耿令新等[22-23]研究了移栽机的振动特性,前者运用有限元分析软件获得了移栽机的模态参数,后者针对移栽机工作时振动影响取苗、顶苗的稳定性,采用时频分析和功率谱密度分析相结合的方法研究了不同工况下各拾振点的振动特性。Servadio等[24]通过振动传递研究拖拉机驾驶室座椅位置的振动问题。王丙龙等[25]研究了果园采摘平台,通过建立人-采摘平台的振动模型,模拟了不同工况下的低速振动试验。
综上可知在农业收获机械的振动测试与特性分析方面已取得相关研究成果,但尚未清楚秸秆还田机在不同工况下的振动特性。因此,本文通过对秸秆还田机建模,运用ANSYS 软件研究机壳和刀辊轴的固有频率,通过非田间振动测试获得时域信号和频域分布规律,对比分析得到拾振点处是否发生共振现象,以期为秸秆还田机避免共振危害、结构动力特性分析及保障寿命等研究提供参考。
1 秸秆还田机有限元建模与分析
1.1 秸秆还田机结构及工作原理
1JH-185 型秸秆还田机通过三点悬挂与拖拉机挂接,其技术参数如表1 所示。
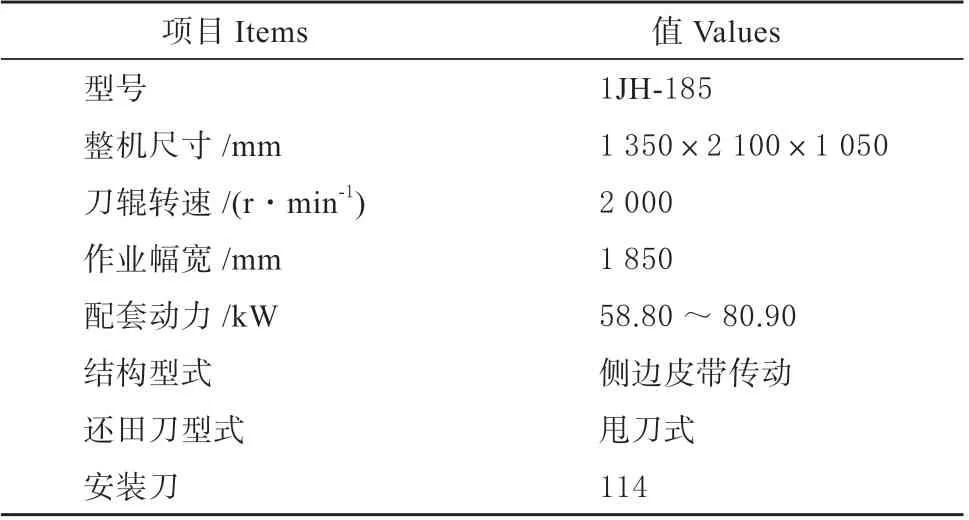
表1 秸秆还田机技术参数Table 1 Technology parameters of straw returning machine
秸秆还田机装置主要由镇压装置、刀具、刀辊、侧变速箱、壳体等组成。该装置中的刀辊为顺时针旋转,刀辊转动支承在机壳两侧,在机壳外有传动副连接在刀轴上。整机结构如图1 所示。刀辊轴焊合由刀辊轴、刀具及轴承组成,其结构如图2 所示。工作时,整机与拖拉机通过三点悬挂装置连接,动力由拖拉机后侧的动力输出轴传出。因秸秆还田机的减速箱轴与拖拉机动力输出轴不能始终保持在同一直线上,所以拖拉机与整机之间以万向节联接,经变速器将动力传送给刀辊轴使其高速旋转。
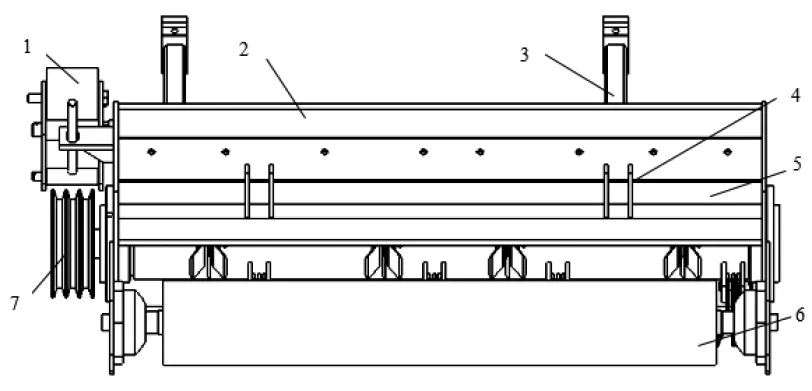
图1 秸秆还田机整机结构图Fig.1 Whole structural drawing of the straw returning machine
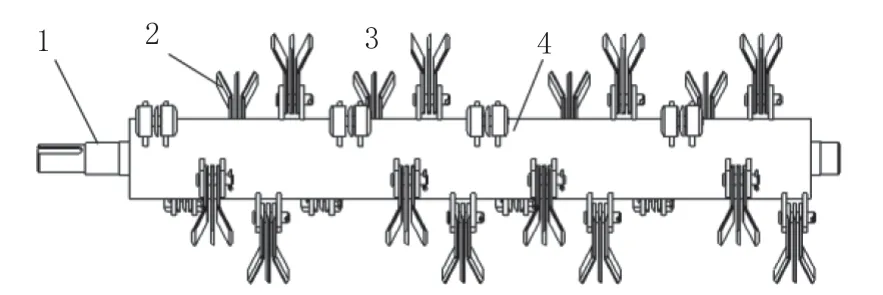
图2 刀辊轴焊合结构图Fig.2 Welding structural drawing of the knife roller shaft
1.2 机壳、刀辊轴建模
机壳主要由端板、折弯板、支撑梁、联接方管、轴瓦、不等角铁、等边角铁、耳板等组成。刀辊轴主要由轴管、长轴头、短轴头等组成。通过Solidworks 创建机壳、刀辊轴的三维模型,分别如图3、图4 所示。
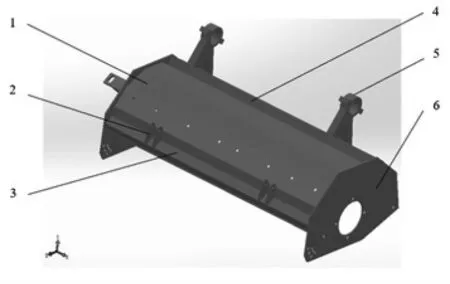
图3 机壳三维模型Fig.3 3D model of the shell

图4 刀辊轴三维模型Fig.4 3D model of the knife roller shaft
1.3 机具部件有限元分析
采用Solidworks 软件对机壳和刀辊轴实体建立模型,以Parasolid 格式保存,导入ANSYS Workbench 中进行有限元分析。为了方便快速计算出有限元模型,可对模型进行适当简化,忽略对模型网格划分质量影响不大的部分倒角和安装孔。根据姚艳春等[18]关于农机结构有限元模态分析网格及单元设置方法添加材料、划分网格并施加约束。其中轴类零件等材料采用45 钢,其余结构均采用Q235,螺栓连接采用刚性Rigid 单元模拟,材料特性如表2 所示。
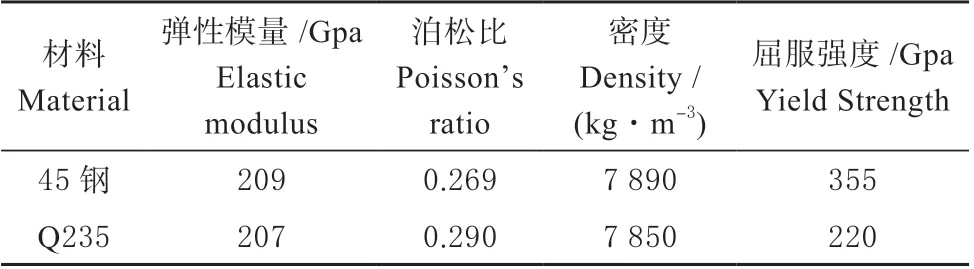
表2 秸秆还田机主要性能参数Table 2 Main performance parameters of the straw returning machine
分别保留机壳和刀辊轴部分,去除机具其余结构,对其进行网格划分,设置机壳和刀辊轴网格最小单元尺寸0.5 mm,其网格划分结果如图5(a)和5(b)所示。网格划分后得到机壳单元391 676 个,节点802 961 个;刀辊轴单元296 311 个,节点520 760个。对模型进行网格质量检查,得到网格雅可比值和纵横比值均大于1,扭曲因子和平行误差大于0°,偏斜度值介于0~1 之间。
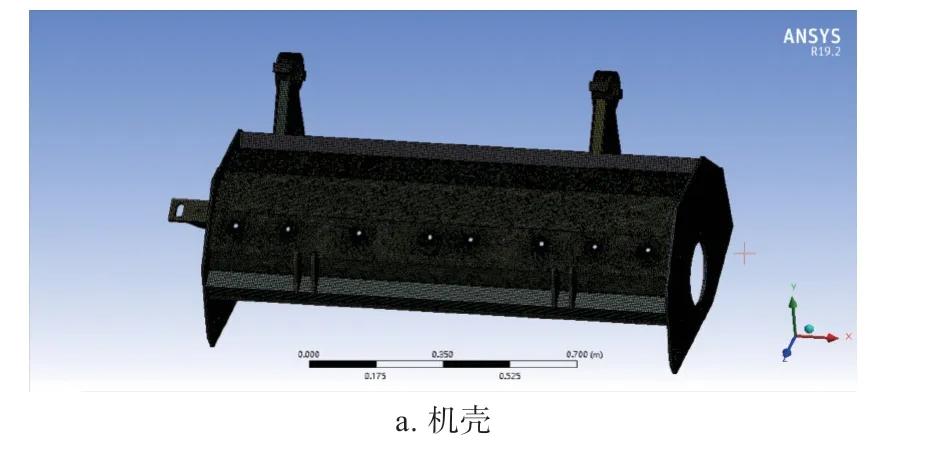
图5 机壳和刀辊轴网格划分Fig.5 Meshing of shell and knife roller shaft
2 模态分析
2.1 模态分析理论
由弹性力学有限元分析方法可知,机械结构一般振动的微分方程可表示为
式中:x—节点位移向量;
x—速度向量;
x—加速度向量;
M—质量矩阵;
C—阻尼矩阵;
K—刚度矩阵;
F(t)—外界激励。
在求解秸秆还田机的结构固有频率和振型中,几乎不受阻尼影响。所以其固有频率可通过分析结构在无荷载的动态响应获得,即外界激励F(t)=0 和阻尼C=0,则其微分方程(1)变为
假设系统的各坐标做同步谐振动,式(2)的解可表示为
式中:A—节点振幅;
T—时间变量;
ωn—固有频率;
φ—相位角。
将(3)式代入(2)式,并消去sin(ωnt+φ),得到
令B=k-,则称B为特征矩阵,从而可以得到该系统的特征方程为
2.2 模态计算
机壳和刀辊轴作为秸秆还田机的重要部分,在内外载荷作用下,因所受的激振力大小随机不定和频率范围宽而引起共振现象导致破坏和噪声。模态分析可得到机壳和刀辊轴前12 阶的固有频率、频率阶数及振型云图。秸秆还田机工作稳定性主要取决于低阶模态特性。
2.2.1 机壳模态计算 模态计算得到机壳前12 阶模态频率如表3 所示。
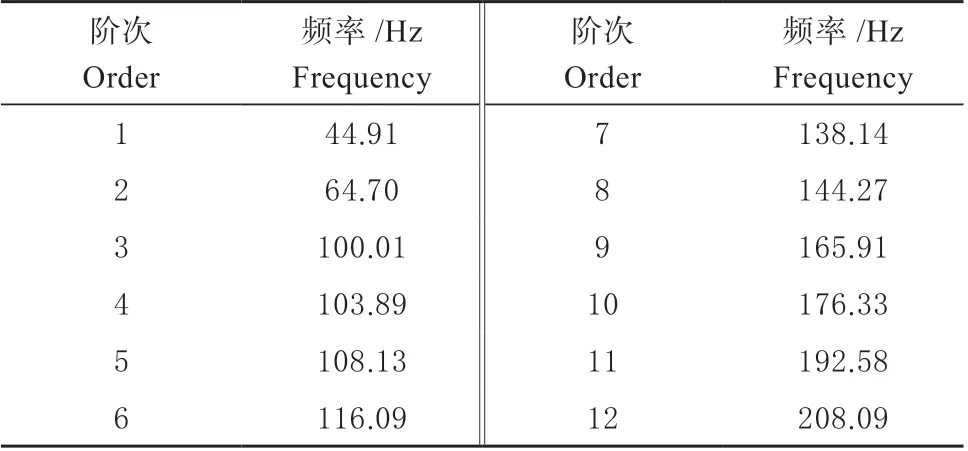
表3 机壳模型前12 阶模态及对应频率Table 3 Corresponding frequency of the 12 steps modes of the shell
结合秸秆还田机机壳工作实际情况的主要激振频率提取前1、4、6、8、9 和12 阶模态频率和模态振型,分别如图6(a)、6(b)、6(c)、6(d)和6(f)所示。
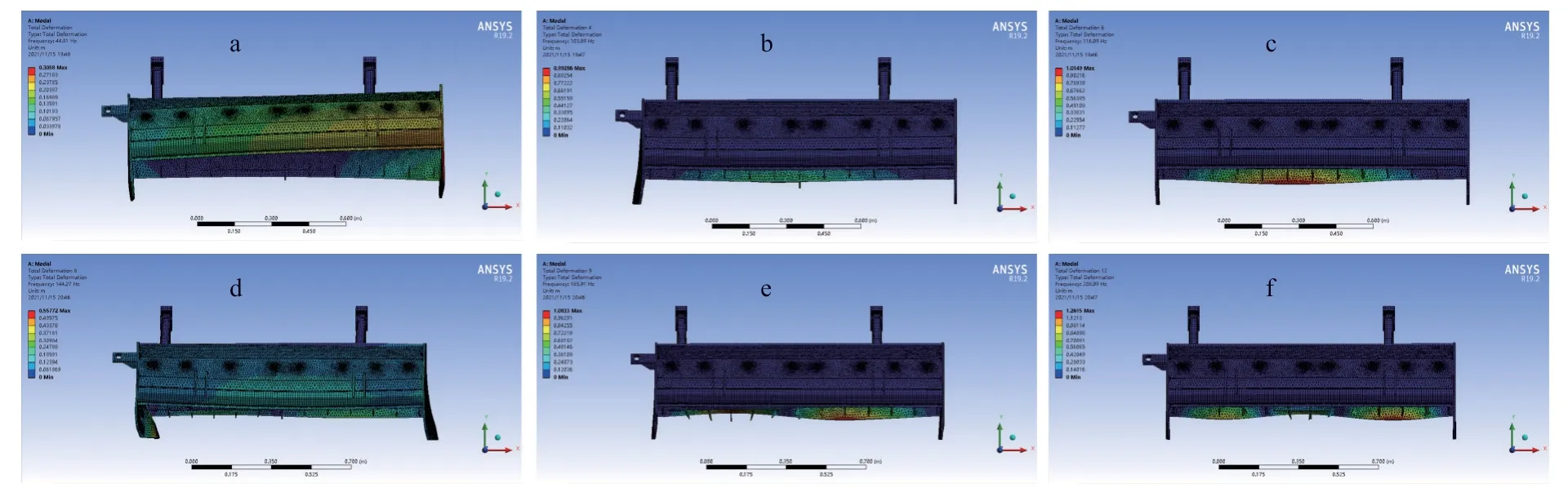
图6 机壳模态振型及频率Fig.6 Modal shape and frequency of the shell
机具壳体主结构的1 阶和4 阶的固有频率分别为44.91 Hz 和103.89 Hz;6 阶和8 阶固有频率分别为116.09 Hz 和144.27 Hz;9 阶和12 阶的固有频率分别为165.92 Hz 和208.09 Hz。
由图6 可知,机壳1 阶模态在X轴向发生扭转,最大变形发生在机壳右端板处,机壳2 阶和3 阶模态在耳板位置发生沿着X反向的偏斜,机壳9 阶模态和12 阶模态在机壳接近镇压轮位置在Z轴向发生扭转,其次变形分布于挂接位置和耳板处,折弯板的变形最小。表明当机具机壳受到该频率的外界激励时,易导致其机壳耳板、机壳壳身及机壳端盖处振动频率较大。
2.2.2 刀辊轴模态计算 通过模态计算得到刀辊轴前12 阶模态频率,结果如表4 所示。
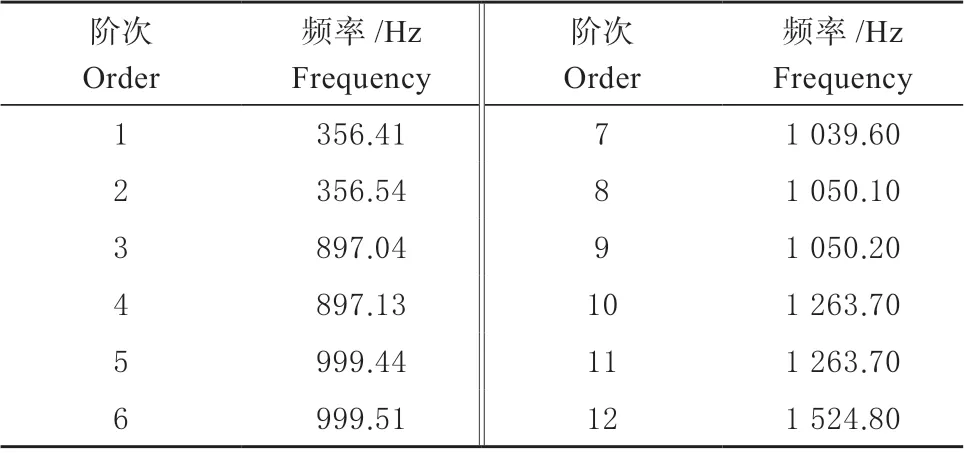
表4 刀辊轴前12 阶模态频率Table 4 Corresponding frequency of the 12 steps modes of the knife roller shaft
结合秸秆还田机刀辊轴工作实际情况的主要激振频率提取前1、2、3、4、5 及6 阶模态频率和模态振型,分别如图7(a)、7(b)、7(c)、7(d)、7(e)和7(f)所示。
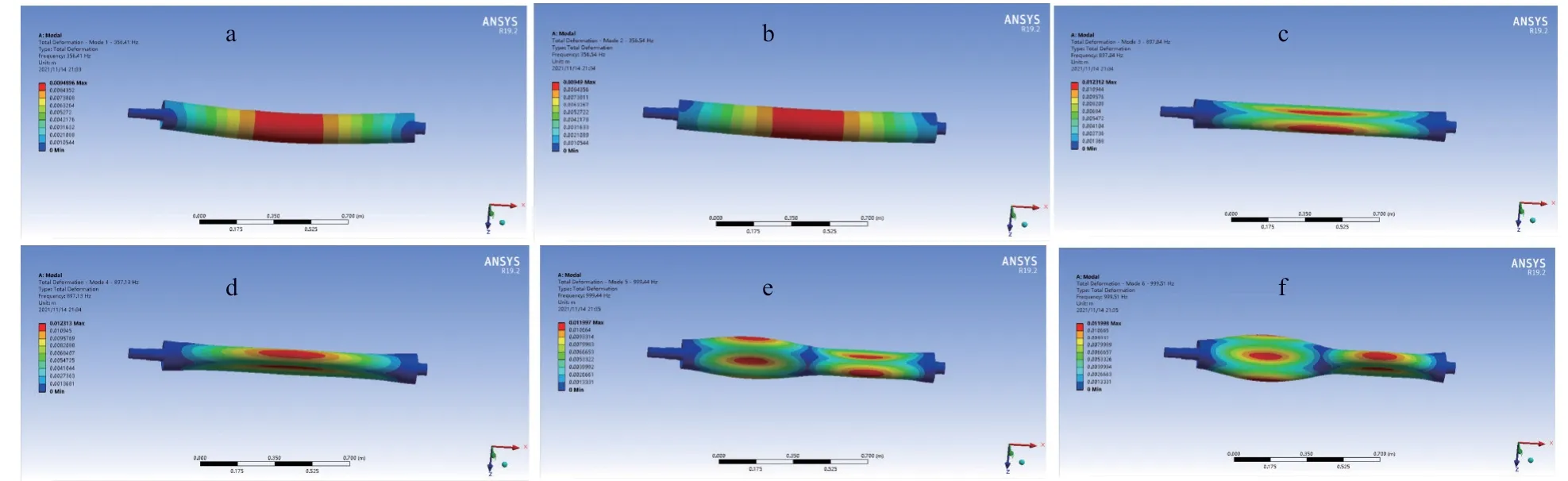
图7 刀辊轴模态振型Fig.7 Modal shape of the knife roller shaft
刀辊轴1 阶和2 阶固有频率分别为356.41 Hz和356.54 Hz,最大变形发生在刀辊轴的中心位置,其转动中心位置变形较大,沿Y轴发生了扭转变形。刀辊轴3 阶和4 阶固有频率分别为897.04 Hz和897.13 Hz,其转动中心发生关于Z轴方向的收缩变形,在Y轴向向外拉伸。刀辊轴5 阶固有频率为999.44 Hz,刀辊轴接近带轮端在Y轴方向发生收缩变形,在另一端发生关于Z 轴向的收缩变形。刀辊轴6 阶固有频率为999.51 Hz,刀辊轴接近带轮端在Z轴方向发生收缩变形,在另一端发生关于Y轴向的收缩变形。表明刀辊轴在受到外界激励时在轴心位置振动变形最大,随着振动频率增加,其变形量由轴心扭转变形逐渐向两轴端移动;刀辊轴的固有振型以弯曲振动为主。
2.3 不同阶次下的模态频率分析
机壳与刀辊轴处在12 阶次模态频率曲线如图8所示。可知机壳与刀辊轴处模态频率随阶次升高逐渐增长。刀辊轴最低模态频率为356.41 Hz,机壳最低模态频率为44.91 Hz,刀辊轴的模态频率高于机壳模态频率。总之,相较于刀辊轴接受振动,机壳接受振动的敏感程度明显小。
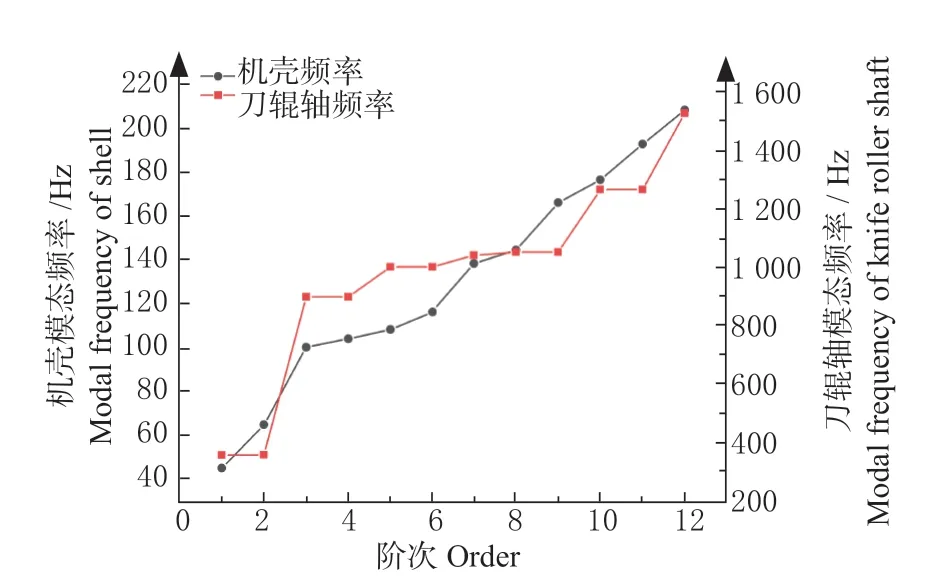
图8 不同阶次下的模态频率Fig.8 Mode frequencies of different orders at the pickup point
3 秸秆还田机非田间振动测试
3.1 主要激振源
秸秆还田机非田间振动试验台的主要激振源为电机,利用(6)式计算出其理论振动频率,结果如表5 所示。

表5 电机转速对应的理论振动频率Table 5 Theoretical vibration frequency corresponding to motor speed
式中:f—理论激振频率,Hz;
n—电机转速,r/min。
3.2 试验条件与设备
2021 年7 月2 日在河北双天机械制造有限公司,以开元刀神1JH-185 秸秆粉碎还田机为试验对象,进行了秸秆还田机振动测试试验。试验设备主要包括DH187E 振动加速度传感器(质量为5.5 g,量程范围为±1×104m/s2,压电式IEPE 型)、DH5923动态信号采集仪(6 通道,采样速率50 Hz)、动态信号分析系统、上海欧多仪器电子公司的信号适调器和笔记本。其工作原理图如图9 所示。
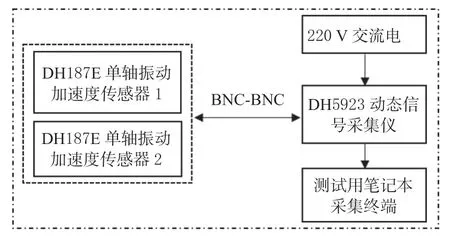
图9 振动试验原理图Fig.9 Vibration test schematic diagram
其中,DH187E 振动加速度传感器可用来采集拾振点处的振动响应信号,传感器将采集到的模拟量信号通过BNC-BNC 转换,经动态信号采集仪输送到笔记本采集终端进行数据处理,得到各阶幅频特性曲线。DH5923 动态信号采集仪每通道均可实现并行和同步采样,单通道采样率可达256 kHz。测试系统在Windows 2008 环境下运行,以DMA 方式长时间、无间断实时传送数据。秸秆还田机振动测试试验采用三相异步电机驱动,符合GB 18 613—2 012 的3 级效率。振动测试现场布置图情况如图10 所示,其中振动测点的布置如图11 所示。

图10 振动测试现场图Fig.10 Vibration test scene
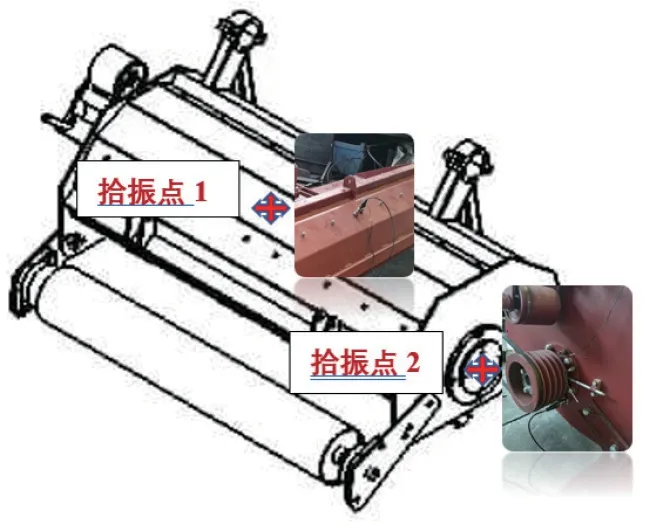
图11 振动测点布置Fig.11 Distribution chart of vibration measurement points
4 秸秆还田机振动特性分析
振动时间信号是设备振动状态的原始表征。设备出现故障时,振动趋势明显增大。因此可通过对振动时间信号观察,初步判断设备的状态。
4.1 时域统计分析
振动状态可用反映振动时间信号的时域特征值表示。常见的时域特征值有:峰值、峰峰值(通频幅值)、均值、均方值、标准差、方差等。对于给定连续信号x(t),各特征值计算公式为:
4.1.1 峰值 信号峰值为信号波形偏离零线的最大偏离值,其计算公式如下:
式中:t—振动测试时间;
xp—信号的偏离值。
振动测试分析系统中,采用时域振动信号的数字序列峰值作为其峰值估计值。
4.1.2 峰-峰值 峰-峰为信号幅值的最大值与最小值之差,即通频幅值,其计算公式如下:
4.1.3 均值 信号的均值E[x(t)]表示信号集合的平均值或数学期望值,用ux表示。基于随机过程的各态历经性,其值为时间段T内的幅值集合的平均值,表达式如下:
式中,ux—信号集合的数学期望值;
T—信号可用时间段。
在振动测试中,将信号数字序列均值作为其均值的估计值,描述振动信号的静态分量。
式中,u^x—信号数字序列均值。
4.1.4 均方值 以振动信号x(t)的均方值E[x2(t)]作为衡量振动强度大小的依据,可较好地反应结构振幅与能量强度,其计算如式(12)所示。
4.1.5 标准差及方差 信号的标准差和方差分别被定义为:
其中,σx—均方差或标准差。
4.2 频谱分析
频谱分析是振动故障诊断中最基本最实用的信号分析技术,其利用傅里叶变换将振动信号变换成自变量为频率的频谱函数形式,揭示信号中包含的不同频率的周期信号。振动信号的傅里叶变换可被定义为:
式中,X(f)—信号的频谱。
由于实际振动信号通常不满足傅里叶变换条件,一般通过求信号的功率谱获得信号的频率成分信息。信号的功率谱定义为其自相关函数的傅里叶变换。对于长度为T的有限长时间信号,功率谱PT(f)和幅值谱|XT(f)|的关系为:
4.3 试验结果与分析
4.3.1 时域分析 为了保证测试波形准确性,在动态信号分析系统中设置采样频率为5 kHz,采样方式为连续采样,开启6 个通道,每次采样前进行通道平衡清零操作,设置完成后进行信号采集。启动秸秆还田机,使机械逐渐运行平稳,每个拾振点采集5 次数据,每次采集60 s,获得机具在2 个拾振点的振动时域波形。高速运行工况下各拾振点的时域波形如图12 所示。
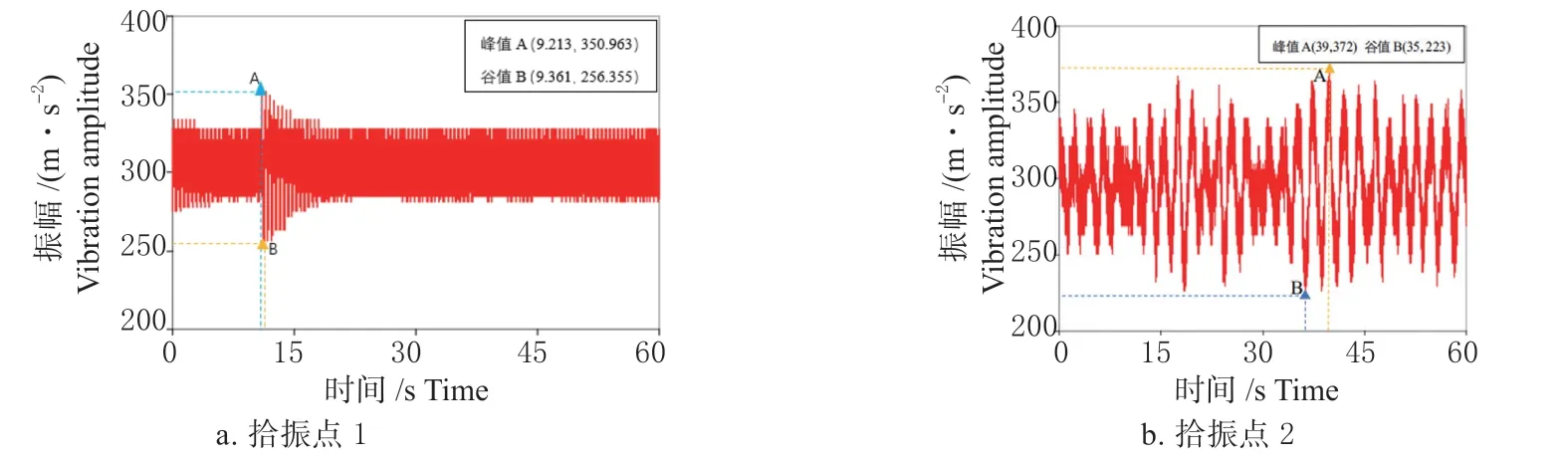
图12 高速工况下输出响应的时域波形Fig.12 time domain waveform output response under highspeed conditions
由图12(a)可知,在60 s 的时间历程中,振动信号仅在10 ~25 s 时间段内波动较大,且峰值和谷值也出现在该波段,即当时间为9.21 s 时,机壳振动加速度峰值(最大值)为350.96 m/s2,当时间为9.36 s 时,机壳振动加速度谷值(最小值)为256.36 m/s2,其他时间段内振动信号波动整体较为平稳,振动信号加速度值集中于270 ~330 m/s2。
由图12(b)可知,振动信号在0 ~15 s 时间段内和45 ~60 s 时间段内信号波形较为平稳,在30 s 附近出现信号波动减弱趋势,振幅降低,在15 ~45 s内出现最小振幅区间。峰值与谷值落于30 ~45 s 时间段内,当时间为39.37 s 时,最大振幅(峰值)为372 m/s2,时间为35 s 时,振幅最小(谷值)为223 m/s2。拾振点1 和2 处的时域参数如表6 所示。
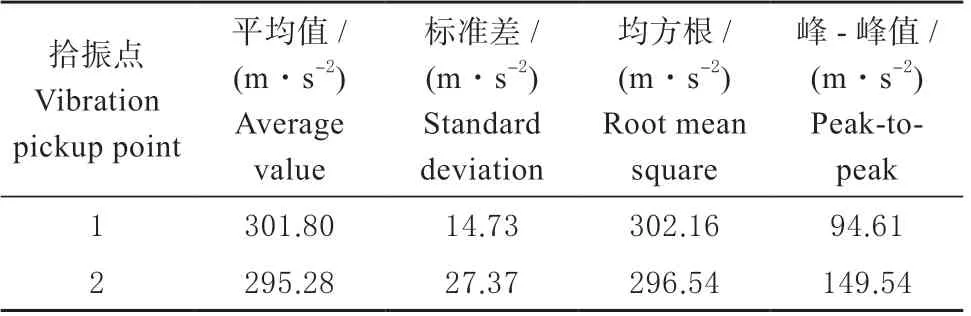
表6 不同拾振点处时域参数值Table 6 Time domain parameter values at different monitoring points
由表6 可以看出:拾振点1 的振幅平均值及均方根均大于拾振点2 处,拾振点2 处峰-峰最为明显。拾振点1 处均方根值普遍高于拾振点2 处。
4.3.2 功率谱分析 对时域信号做快速傅里叶变换分析,得到拾振点1 和2 处的频域波形,如图13 所示。由图13(a)可知,拾振点1 频谱峰值点主要集中于频率0 ~160 Hz 范围内,其间出现10 个峰值点(1 ~10)。拾振点1 振动频率在1 点处出现最大振幅峰值点,即频率为49.81 Hz 时,存在最大振幅为25.19 m/s2。峰值6 点处出现最大频率为150.39 Hz,对应振幅-2.84 m/s2,该点频率接近机壳8 阶和9 阶模态固有频率,其值分别为144.27 Hz和165.91Hz,容易与之发生共振。
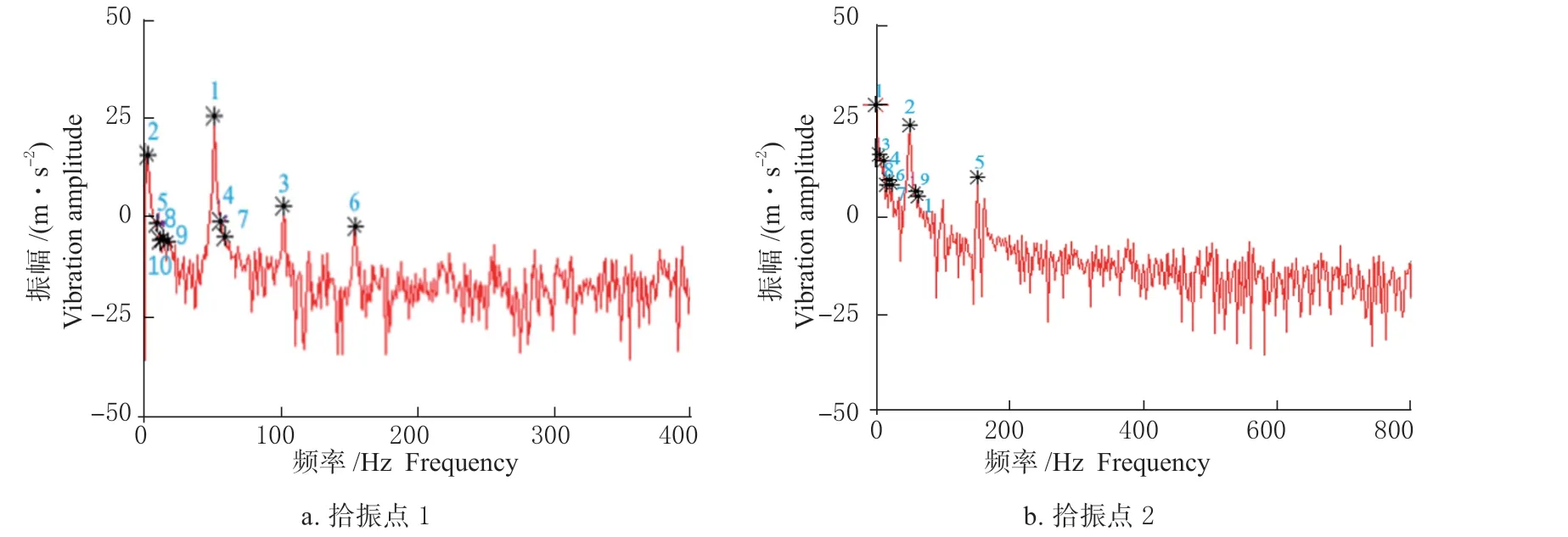
图13 输出响应的频域波形Fig.13 Output response frequency domain waveform
由图13(b)可知,拾振点2 频谱峰值点主要集中于频率0 ~160 Hz 范围内,其间出现10 个峰值点(1 ~10)。拾振点2 振动频率在1 点处出现最大振幅峰值点,即频率为1.95 Hz 时,存在最大振幅为31.96 m/s2。峰值4 点处出现最大频率为150.39 Hz,对应振幅9.35 m/s2,该点频率低于刀辊轴1 阶模态固有频率356.39 Hz,更加远低于刀辊轴前12 阶模态固有频率,不易与之发生共振。
5 结论
(1)建立了秸秆还田机的有限元模型,运用ANSYS 软件分别对机壳与刀辊轴做网格划分及模态分析,得到了各自结构的前12 阶固有频率与模态振型。
(2)经有限元模态计算与非田间振动试验,机壳的固有频率远小于刀辊轴固有频率,机壳在发生振动时更容易受迫振动。
(3)通过振动试验研究可知,该秸秆还田机能够满足实际工况,能保障机具寿命,为结构动力特性的分析和结构优化提供参考。

