三次方程根的问题之变式探究

赵寿锋

(河北省沧州市第一中学)

导数作为高考的必考内容,主要考查函数、方程、不等式等问题的综合应用,诸如方程的根和函数零点问题等.利用导数及数形结合思想可以很好地解决方程根的问题.本文以变式探究的形式介绍利用导数法讨论方程根的问题,供大家参考.

题目 三次方程x3－6x2＋9x－10＝0的实数根的个数为_________.

令f(x)＝x3－6x2＋9x－10,则f′(x)＝3x2－12x＋9,所以f′(x)＝3(x－1)(x－3).当x＜1 或x＞3时,f′(x)＞0,f(x)单调递增;当1＜x＜3时,f′(x)＜0,f(x)单调递减.于 是f极大值(x)＝f(1)＝－6＜0,所以f(x)的极大值小于零,其图像如图1所示,则f(x)的图像与x轴仅相交于一点,故三次方程实根的个数为1.

图1

本题的解法为在实数范围内探求一元高次方程的实数根的个数提供了一种行之有效并容易实施的方法,即先用导数法求出方程所对应的函数的极大值和极小值,如果不存在极大值与极小值,那么该方程仅有一个实数根;反之,可根据极大值与极小值的符号对根的分布进行判断,这种解法也体现了函数与方程的关系.

变式1 设a∈R,试探讨关于x的三次方程x3－3x2－a＝0的不同实数根的个数.

先把方程变形为

令f(x)＝x3－3x2,则f′(x)＝3x(x－2),所以通过列表(如表1)来讨论该三次函数的单调区间和极值情况.

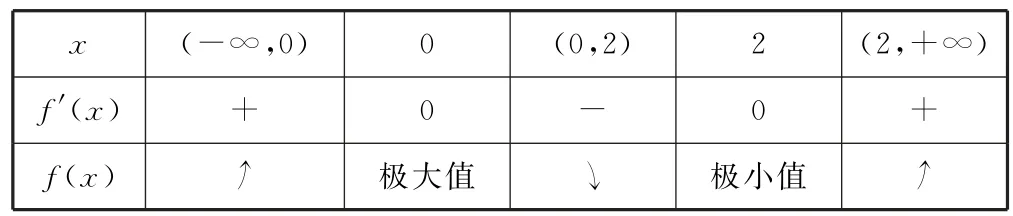
表1

因此f(x)的极大值为f(0)＝0,极小值为f(2)＝－4,函 数y＝f(x)的大致图像如图2所示,由于方程①的不同实数根的个数就是函数f(x)的图像和直线y＝a的交点的个数,所以根据图像有下列结论:

图2

当a＜－4或a＞0时,原方程有1个根;当a＝－4或a＝0时,原方程有2个不同的实数根;当－4＜a＜0时,原方程有3个不同的实数根.

(1)染色体编码 本文采用ARMAX模型，参数部分为实数，因此需要对量子个体进行编码，根据参数的个数决定每个个体的染色体长度。量子位表示为

本变式与引例的不同之处是含有参数a,通过参变分离法,把原方程的根的个数问题转化为一个三次函数图像与一条平行于x轴的动直线的交点问题,体现数形结合思想与分类讨论思想的完美结合.

变式2 已知函数f(x)＝x4－4x3＋4x2－1,问是否存在实数b,使得函数g(x)＝x4＋bx2＋1(其中b＜4)的图像与函数f(x)的图像恰有3个交点,若存在,求出b的取值范围;若不存在,说明理由.

函数g(x)与f(x)的图像恰有3个交点,就是方程g(x)＝f(x)有3个不同的实数根,即x4＋bx2＋1＝x4－4x3＋4x2－1有3个不同的实数根,即三次方程4x3＋(b－4)x2＋2＝0有3个不同的实数根.令h(x)＝4x3＋(b－4)x2＋2,则h′(x)＝12x2＋2(b－4)x.

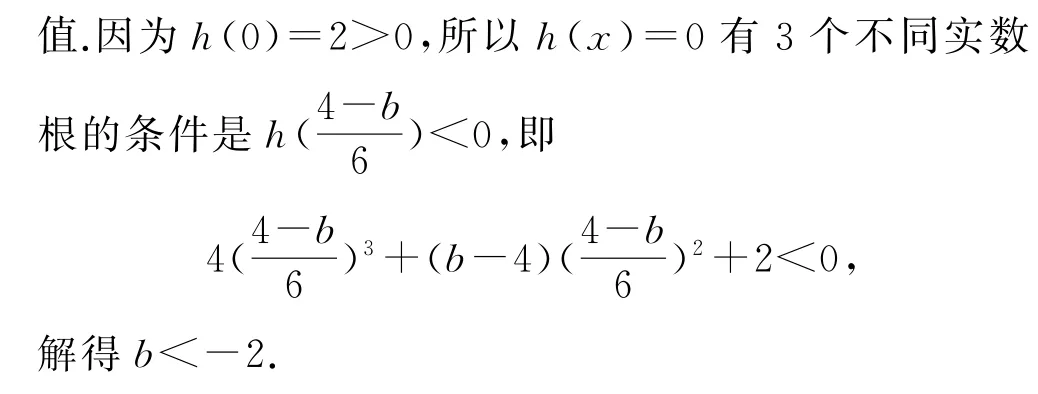
本变式的解答过程给我们揭示了一元三次方程的实根个数的判别方法,具体如下.

设f(x)＝ax3＋bx2＋cx＋d,则f′(x)＝3ax2＋2bx＋c,若a＞0,则Δ＝4(b2－3ac).如图3-甲所示,当Δ≤0时,f(x)在R 上单调递增,所以f(x)只有一个零点;当Δ＞0时,方程f′(x)＝0有两个不同的实数根x1,x2(x1＜x2),那么f(x)在x1处取到极大值,在x2处取到极小值.当f(x2)＝0(如图3-乙)或f(x1)＝0(如图3-丙)时,f(x)＝0有3个根,其中2 个是重根;当同时出现f(x1)＞0 和f(x2)＜0的情形(如图3-丁)时,f(x)＝0必有3个不同的实数根.

图3

变式3 已知三次函数f(x)＝x3－x.

(1)设M(λ0,f(λ0))是该函数图像上的一点,试求该点处的切线方程;

(2)证明:过点N(2,1)存在3 条直线与曲线f(x)＝x3－x相切.

(1)由f(x)＝x3－x,得f′(x)＝3x2－1,设过点M(λ0,f(λ0))的切线方程为y－(λ30－λ0)＝(3λ20－1)(x－λ0),即

(2)由(1)可知曲线上点M(λ0,f(λ0))处的切线方程为y＝(3λ20－1)x－2λ30.若切线过点N(2,1),则存在λ,使1＝2(3λ2－1)－2λ3,即2λ3－6λ2＋3＝0,于是原问题等价于方程2λ3－6λ2＋3＝0有3个相异的实数根.

设g(λ)＝2λ3－6λ2＋3,则g′(λ)＝6λ2－12λ＝6λ(λ－2).令6λ(λ－2)＝0,可得极值点为λ1＝0,λ2＝2,函数g(λ)的单调区间与极值分布如表2所示.

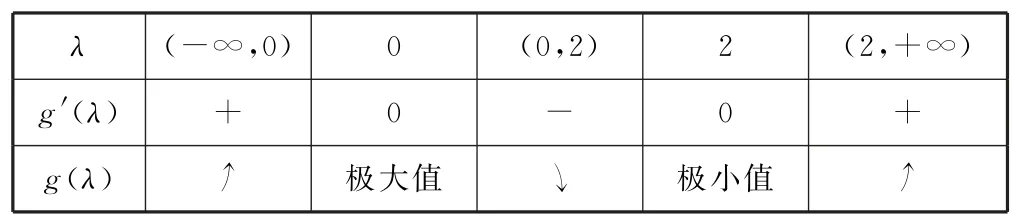
表2

由表2可知g(λ)在R上仅有1个极大值与极小值,且极大值为3,极小值为－5,所以函数g(λ)有3个零点,即方程2λ3－6λ2＋3＝0有3个相异的实数根,即过点N(2,1)存在3条直线与曲线f(x)＝x3－x相切.

本变式的第(2)问是函数切线条数问题,求解时是将之转化为三次方程根的解的个数问题来处理的,由此可见构造新函数,用导数的观点来研究函数的零点个数,是一种基本的方法.

变式4 已知函数f(x)＝x3＋3bx2－2b3在(－∞,0)上单调递增,在(0,2)上单调递减,如果方程f(x)＝16恰好仅有1个解,试求实数b的取值范围.

因为函数f(x)在(－∞,0)上单调递增,在(0,2)上是单调递减,又由f′(x)＝3x2＋6bx＞0,可得x∈(－∞,0)∪(－2b,＋∞),b＜0.由f′(x)＝3x2＋6bx＜0,可得x∈(0,－2b),于是由题意有(0,2)⊆(0,－2b),所以2≤－2b,即b≤－1.

又f(x)在(－∞,0)和(－2b,＋∞)上是增函数,在(0,－2b)上是减函数,其图像大致如图4 所示,所以函数f(x)在[0,－2b]上的值域是[f(－2b),f(0)]＝[2b3,－2b3],从图像可以看出,若方程f(x)＝16恰好仅有1个解,则只需－2b3＜16,即b＞－2.

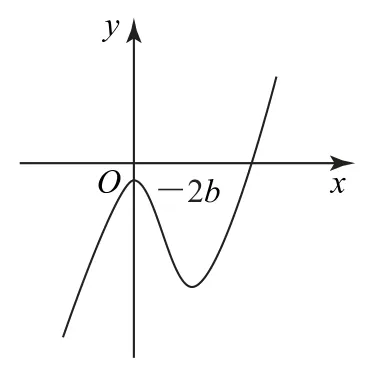
图4

综上,实数b的取值范围(－2,－1].

本变式具有较强的综合性,且具有一定难度,体现了导数的逆向应用,但基本方法没变,还是利用导数,从研究函数的图像入手.

从以上分析可以看出,三次方程根的问题通常可以转化为三次函数的零点问题,利用导数研究函数图像的变化趋势,从而使问题迎刃而解.

(完)