一个新的强化学习多序列对比工具CDRL
王韦添,江育娥
(福建师范大学计算机与网络空间安全学院,福建 福州 350117)
多序列比对(multiple sequence alignment,MSA)是生物信息学中最重要的研究内容之一,它几乎应用于生物信息学的所有研究领域[1].MSA最直观的应用就是可以利用其所蕴含的生物序列信息,来描述物种之间进化距离的系统发育树.MSA在生物信息学中主要是被用来排列DNA、RNA或蛋白质的初级序列,以寻找它们之间相似区域.MSA同样可以用于药物设计和药物开发,其中相似的序列区域匹配、二级结构和功能信息推断有助于药品的研发工作[2].
MSA需要通过插入间隙来使得每条序列都达到相同长度并对齐.因为其是个NP完全问题,所以想要得到最优解往往是不可能的.因此许多启发式方法和算法被应用于MSA问题,希望得到序列的较优解,如使用自定义操作的遗传算法、隐马尔可夫模型、模糊逻辑强化学习和许多其他工具[3],其中渐进式对齐方法的实现过程较为简单,现在很多常用的对齐工具都是基于渐进式对齐开发的,例如MAFFT[4]、MUSCLE[5]、PASTA[6]、UPP[7]和MAGUS[8].
强化学习需要定义奖励和动作,通过执行动作从外界获取奖励回馈,不断重复这个过程,将策略稳定下来[9].强化学习MSA的做法就是将对齐过程拆解开来,每个时间步执行一个动作,每个动作都会有奖励返回,不断地累计奖励直至对齐结束.通过这样的方式对空间进行探索,得到多个可行解以及他们对应的累计奖励.随后利用策略更新算法对得到的可行解进行进一步迭代,最后得到的策略就为序列对齐的方案.部分强化学习MSA算法将序列的局部对齐作为研究对象,定义一个固定大小的“棋盘”,使用类似下棋的方式将序列碱基填入棋盘,并不断迭代得出最佳对齐[10].但是这种方法需要先确定对齐长度,而且该方法不适用于长序列对齐.所以大部分的强化学习MSA模拟渐进式对齐算法的思路,以序列的加入顺序作为动作,首先不断尝试不同的序列对齐组合,得到多个可行解,随后对可行解进行更新迭代,最后得到一个较好的策略[11].由于强化学习MSA对序列的加入顺序进行了大量的尝试,所以得到的结果往往优于其他算法.
在MSA中,现有强化学习算法的计算复杂度非常高,因为需要投入网络学习的数据维度为O(n2),这使得强化学习无法适用于大规模数据集.因此,目前还没有成功将强化学习算法应用于大数据集样本的先例.在强化学习MSA中,智能体需要不断与空间交互,在这个过程中不断优化自己的策略.强化学习MSA网络的收敛速度取决于问题的复杂程度,由于MSA问题的复杂程度很高,因此该网络难以收敛.为了避免重复计算,一些强化学习MSA使用哈希函数来存储中间的对齐过程.然而,现有的方案使用的序列数不超过12条.
为了使用强化学习MSA来解决较大数据集,提出了一种新的强化学习结构CDRL(contextual deep reinforcement learning).CDRL利用上下文关系将网络输入维度减小到与序列数量n同等量级,即O(n),这种方法跟现有方法的网络输入维度O(n2)相比,输入数量极大减少.CDRL的网络收敛速度比其他模型快,实验结果表明,CDRL的性能优于当前业界其他方法.跟其他模型使用的12条序列数据相比,CDRL使用了100条序列,因此CDRL可以适用于较大数据集.
1 相关工作
首先介绍渐进式MSA的一般实现流程,并详细说明几种常用的方法.此外还将阐述强化学习在MSA中的实现思路和实现流程,并对几种常用的强化学习MSA算法及其存在的问题进行描述.
1.1 渐进式MSA方案实现过程介绍
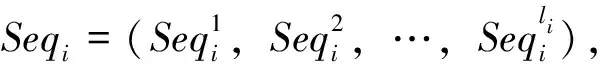
用AlignSeq表示来自列表Seq的序列最佳比对矩阵(按Seq1,Seq2,…,Seqn的对齐顺序考虑).这种比对意味着序列按如下方式逐步比对:Seq1先与Seq2比对,然后得到的对齐结果与Seq3比对.再将获得的对齐结果与Seq4对齐,并继续迭代该过程,直到所有序列Seq1,Seq2,…,Seqn完成对齐,这样就完成了渐进式多序列比对的任务.此外,其他对序列进行比对的方法还有图聚类和最长公共子序列等,这些方法的实现过程虽然简单易懂,但是效果不理想.对于对齐的结果,业界通常采用SP分数[13]进行评价.
如上所述,渐进式MSA目的为找寻Seq中具有最大SP分数的序列对齐结果[14].从计算的角度来看,对于一个序列来说,渐进式MSA可以看作是寻找一个最大化SP分数的序列选取顺序.具体来说,可以把序列比对的得分定义为Score(Seqσ),其中Seqσ=(Seqσ1,Seqσ2,…,Seqσn),σi∈{0,1,2,…,n}.渐进式MSA的工作就是要最大化Score(Seqσ)[15].常用的渐进式MSA方案有MAFFT[4]、MUSCLE[5]、PASTA[6]、UPP[7]和MAGUS[8],渐进式MSA一般可分为4个流程,且将整个问题拆分为多个小的对齐任务来解决.总体上,可以按图1的形式对渐进式对齐方案进行归纳.
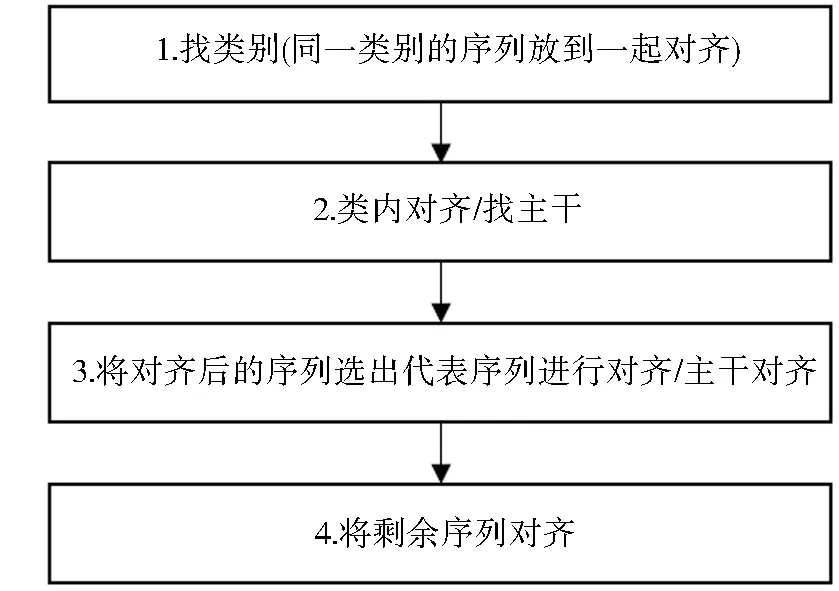
图1 渐进式对齐方案流程图Fig.1 Progressive alignment scheme flowchart
MAFFT需要以输入序列都是同源序列作为所有操作的前提,即输入序列来自一个共同的祖先[16].一般来说MAFFT需要建立一棵系统发育树[17],随后将序列慢慢加入这棵树中,加入完成后,对于叶子节点先进行对齐,并逐步向根节点进行对齐.MUSCLE对一双序列使用两种序列距离度量:k-mer距离(用于未对齐的序列)和Kimura距离(用于对齐的序列)[18].利用2个距离进行聚类,随后进行对齐工作,最后进行剪枝操作[19],完成对齐任务.PASTA采用迭代策略,每次迭代涉及6个步骤.第一次迭代从起始树开始,随后的迭代从前一次迭代中估计的树开始[20].在每一步中,引导树用于将序列集划分为更小的子集,以这些子集为节点构建生成树.生成的MSA集合相互重叠,并且它们在重叠的地方是兼容的[21].这些属性使其能够使用传递性合并这些重叠的MSA,并在整个序列集上生成一个MSA的对齐结果.MAGUS首先设计一个主干序列库,并把主干序列库随机分成n个小类,每个小类中的序列数相同,随后对于n个小类随机抽取等量的序列作为主干序列[22].得到主干序列后,计算相邻序列碱基的相关性,并将其作为权重生成一个无向图,随后MAGUS使用图聚类算法对生成的无向图进行图聚类操作.图聚类完成后,MAGUS对生成的图进行误差排除,去除一些明显的错误,最后生成的结果就是主干序列对齐结果[23],最后将非主干序列与主干序列对齐结果进行对齐.UPP的输入是一组需要对齐的序列,该序列数据集分为2个部分:主干数据集和查询序列集[24].首先把主干数据集进行对齐,基于主干对齐结果建树,得到主干对齐和对应的树之后,构建子树(HMM)的集合[25],然后将查询序列与每个HMM对齐,并根据每条序列的最佳评分HMM将查询序列添加到主干对齐的相应位置.
综上,现有的渐进式多序列比对方法还存在几个难以克服的问题,在这些问题中,有一个核心的问题在于这些渐进式方法通常只使用单一的启发式算法来得到对齐结果,这样的做法可能会导致得到次优解或局部最优解.
1.2 强化学习MSA介绍
针对渐进式MSA中存在的核心问题,强化学习被用来解决序列对齐问题.与传统的渐进式方法不同,强化学习的智能体会不断地与环境交互来得到一个对齐方案,而不是基于单一的启发式算法完成对齐任务,所以强化学习算法得到的对齐结果往往优于现有的渐进式算法.
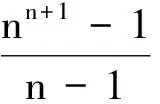
动作空间A由解决问题的代理可用的n个动作组成,并对应于n个可能的值(1,2,3,…,n)用于表示一个解({1,2,…,n}的排列),即A={a1,a2,…,an},其中任意动作ai的取值都是从1到n,即ai=x(∀x∈{1,…,n}).从一个状态s∈S,代理可以通过执行n个可能的动作中的一个进入一个可能出现的后续状态[27].
图2给出了状态空间和状态之间转换的图形表示.圆圈表示状态,状态之间的转换用箭头表示,箭头标有将代理从一个状态引导到另一个状态的动作.强化学习MSA的奖励函数将由式(1)定义:
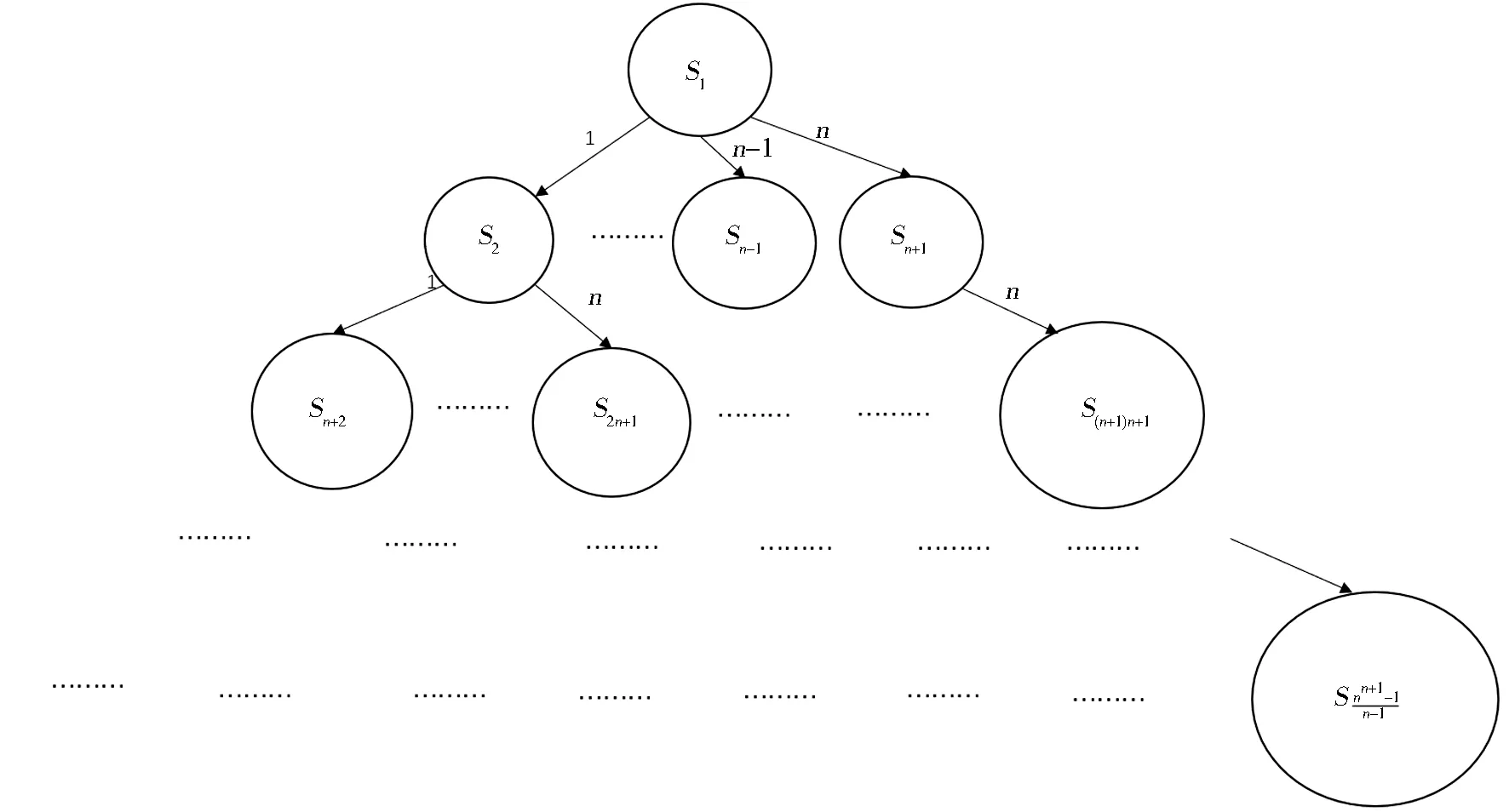
图2 强化学习MSA的状态空间和状态之间的转换图Fig.2 The diagram of state space and state transitions in RL-MSA
(1)
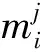
强化学习MSA已经有了一些研究成果,Zhang等[27]提出了一种基于深度强化学习(deep reinforcement learning,DRL)的MSA新方法,受生物反馈的启发,利用负反馈政策(negative feedback policy,NFP)来提高性能并加速模型的收敛.Song等[28-29]提出了一种DQNx-drop方法,通过将x-drop算法与DQNalign算法相结合,无需人工干预即可执行局部对齐的算法.Li等[30]提出了一种基于Actor-Critic模型的Q-learning序列对齐方法.Madhusudhan等[31]提出一个基于分布式深度Q学习的多序列对齐模型.Kundu等[32]提出关于基于强化学习的多序列对齐.Hwang等[33]使用深度强化学习方法解决疫苗设计中的多序列比对问题.
上述强化学习MSA都存在收敛速度慢、网络输入维度大、限制序列输入数量的问题.收敛速度慢是因为强化学习MSA奖励的特殊性,导致其常常不能完成完整轨迹.网络输入维度大的原因是输入数据的编码方式使得输入的维度为O(n2).限制序列输入数量是由于中间对齐存储索引编码特点使得网络不能训练过多的序列.这些问题使得目前的强化学习MSA无法应用于样本量大的数据集,而且在小数据集上的表现也没有达到期望值.因此,业界急需一个能够解决较大样本数据集,并且性能较优的强化学习MSA模型.
2 强化学习模型CDRL
2.1 CDRL的模型架构
采用深度强化学习的框架对数据进行学习.首先,定义3个空间,分别为状态空间、动作空间和奖励空间.状态空间表示当前智能体已选择的序列顺序和序列编号.动作空间大小为n(序列数量),表示每次从序列中抽取的序列号.奖励空间对于奖励的值没有限制,它基于已选取的序列,将它们对齐后的SP分数作为奖励.
图3展示了CDRL探索策略的过程,智能体首先使用随机探索和上下文相关网络进行动作选择,选定动作后对环境进行探索,每一次探索都需要计算相应动作的奖励,奖励计算完毕后需要把相关的经验存入经验池内,在策略迭代的过程中,经验池将不断涌入新的探索内容,强化学习网络将不断抽取经验池中的经验对权重进行训练,以进一步增强网络对于动作选取的正确性.最终,可以得到一个较好的强化学习网络.
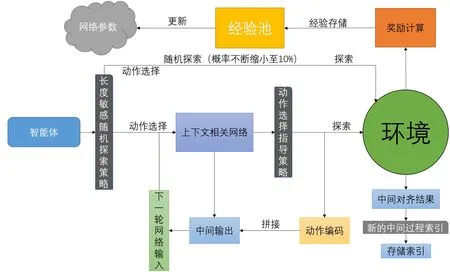
图3 CDRL基本工作流程图Fig.3 Basic workflow diagram of CDRL
在程序运行后,智能体首先对空间进行随机探索(随机抽取的序列).每次抽取序列后,智能体执行对齐操作,并将当前状态、选取的动作和得到的奖励存入经验池,以供后续网络训练使用.随着训练的逐步推进,智能体随机探索的比重将逐渐减小,将更有可能使用先前经验来选择下一步的动作.最终,随机探索的比重将定格在10%.在选取动作的过程中,本次实验加入长度敏感随机探索策略,使得初始选取的动作能够更受网络关注,从而提高重要知识的学习频率,使得网络能够得到更好的结果.在强化学习网络方面,本文提出的新模型,通过上下文的信息使得网络的输入维度减小.在网络选择的过程中,使用动作选择指导策略,加速网络的收敛速度,在相同的探索次数内能够得到更好的实验结果.对于中间过程的存储索引,使用本文提出的编码方式,解除序列数量的限制,使得网络能够训练较多样本.
业界现有的强化学习网络,输入维度为O(n2),其网络参数多,而且训练时间较长,为此提出一个新的深度强化学习MSA模型-CDRL.该模型结合上下文的内容,将网络的输入维度从O(n2)降为O(n),输入维度量级的降低使得CDRL适用较大的数据集样本.在改进网络模型的同时,还提出了另外3点创新策略来进一步提升模型性能,下面分别对前述提到的网络模型、长度敏感随机探索策略、动作选择指导策略和新的索引方式4个创新点进行介绍.
2.2 网络模型
目前业界强化学习MSA网络的输入维度为O(n2),其中输入由当前状态转变而来.因为当选择了n-1条序列后,最后一条序列也就确定下来,所以状态的最大长度为n-1.假设在某个时刻,状态中包含了x条已经选择的序列,那么还需要选择n-1-x条序列.对于已经选择的序列,进行one-hot编码;对于尚未被选择的序列,使用零向量编码.这样的编码方式能够包含已选序列编号和序列选择顺序的信息,同时也存在输入长度过长的问题,所以该编码方式不适用于大样本数据集.
为了解决上述问题,本文提出了一个新的上下文相关网络模型,一种渐进式MSA的解决方案.渐进式MSA本质上是一个文本问题,即通过输入一串未对齐序列,生成一个合适的序列选择顺序,把每个输入看成一个动作,序列选择顺序则就是由一串动作序列组成.为此考虑使用自然语言处理中的模型输入编码方式,通过合适的编码来进一步降低网络的输入维度.
上下文相关网络使用step-by-step LSTM(long short-term memory)的思路,将网络的hidden-state作为上下文信息进行保存,结合下一步的序列信息作为下一次网络的输入,从而降低网络的输入维度.具体地,将网络的第一个输入向量设置为零向量,模拟网络在第一次序列选择时无信息的情况.对于后续的输入,可以使用网络的中间层输出(如图3中间输出节点)作为上下文信息进行保存,并将最近一次选择的动作(如图3动作编码节点)进行one-hot编码,将这2个信息整合成一个向量,作为网络的下一次输入,具体过程见图3.这样整合的下一次输入向量仍然只是一次输入,该操作并不会增加网络的参数量,因此,其输入参数空间复杂度仍然是O(n).相比于业界其他强化学习MSA输入参数空间复杂度的O(n2),CDRL的这种处理方式避免了网络的输入维度的膨胀,使得本文的方法有处理大数据集的可能,即CDRL使得网络的参数量与序列数量呈线性关系,将网络的空间复杂度由现有方法的O(n2)降为O(n).
为了保证每一次的上下文都被保存,智能体在进行随机探索时,也需要将选择的动作输入网络进行学习,以此来保证上下文的连贯性,这样的做法难免会带来一些额外资源消耗,但是,CDRL仍然是线性输入.相较于当前其他方法的O(n2),CDRL输入参数数量大大减少,因此提高了计算效率和空间使用效率.总之,CDRL通过利用前后文的关系,将网络的输入维度减小到O(n)的维度,从而可以较好地处理较大规模的序列数据.
2.3 长度敏感随机探索策略
为了加速训练速度,提出了一种长度敏感随机探索策略.根据选择动作的位置不同,对随机探索和网络学习的比重进行倾斜,即在序列选择的初始阶段,随机探索的概率更大,而越往后的序列,随机探索的概率将逐渐减小,更多地加入之前习得的先验知识.在渐进式MSA方案中,前几条序列的选择比后续序列的选择更加重要,因为它们决定了对齐的主要方向.CDRL更加关注前几条序列(大概率随机探索),这样能够在有限的探索次数内寻找到更多有意义的空间,这种做法与渐进式MSA的思路相吻合.
对于随机探索概率的下降速度,本文采用信息熵的计算方法,利用模拟回报(见图4模拟回报计算节点)来计算网络选择动作回报的混乱程度,这样可以使得随机探索的概率随着序列选择的进行不断减小.
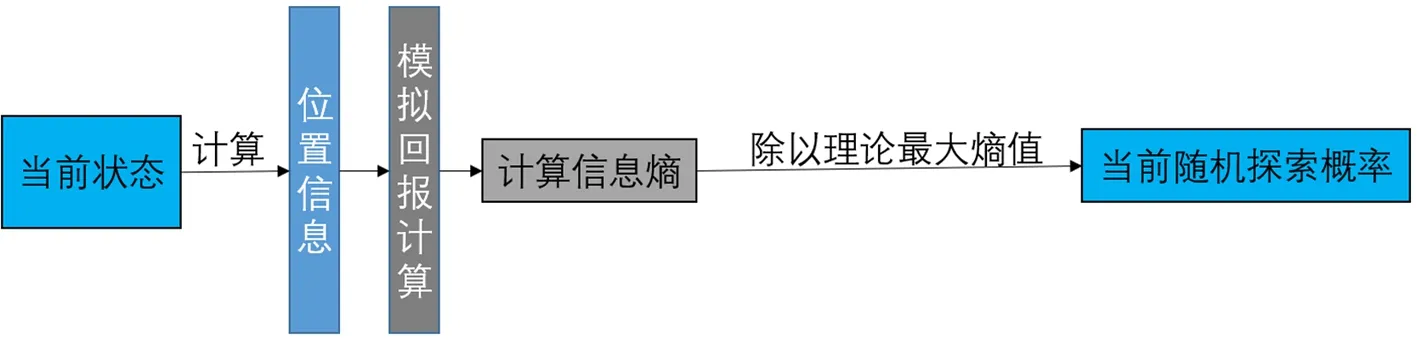
图4 长度敏感随机探索策略流程图Fig.4 Flow chart of length-sensitive random exploration strategy
2.4 动作选择指导策略
强化学习MSA网络在训练过程中很难收敛.在传统的方法中,如果网络选择的动作与之前选择的动作重复,那么本次探索失败,需要返回第一条序列重新探索.这种方法导致网络的收敛速度极慢,甚至于在一次训练结束后,网络都不能完成一次有效的探索,从而浪费了大量的计算资源.因此提出了一个动作选择指导的策略来指导网络,使其不要在一次策略探索中选择同样的动作来避免无效探索.具体而言,使用当前状态来构建一个指导向量(见图5指导向量节点),使用指导向量来指导网络的输出,使得网络不会选择之前已经选择过的动作.这种方法可以让网络每次都能完成有效的探索,并且在有限的探索次数内得到不错的对齐结果.
图5 动作选择指导策略流程图Fig.5 Flow chart of action selection guidance strategy
2.5 新的中间过程索引
为了避免已经对齐过的序列反复执行对齐操作,中间的对齐过程会被存储下来,并且生成对应的索引以便下次使用.当前一般采用哈希函数对当前状态进行编码,将其映射为一个值作为中间对齐的索引,但是这种哈希函数需要预留很多空间以适应未出现的对齐情况.对于n条序列的对齐任务,所有可能的中间对齐数量维度为nn.但在实际探索中只有一部分空间会被探索,因此预留这么多空间是非常浪费的.当前一般采用具体的数字作为中间过程的索引,即对于中间所有可能的对齐,目前大都使用具体的数字来索引定位,这种操作不是必须的.
针对上述问题,提出了一种新的中间过程索引方式,使用当前状态来编码一段字符作为中间对齐结果的索引.为了让索引长度相等,设计的编码方式会读取序列数量的维度信息(见图6读取维度节点),并将当前状态中的每个动作编码为等长的字符串,剩余的未选动作则填充为相应长度的零字符串,随后将这2个字符串拼接起来作为当前对齐结果的索引.这种编码方式避免了使用具体的数作为索引,更大的好处是因为索引是动态的,不需要为未出现的对齐情况预留空间.这节省了大量不会被使用到但是却预留的空间.
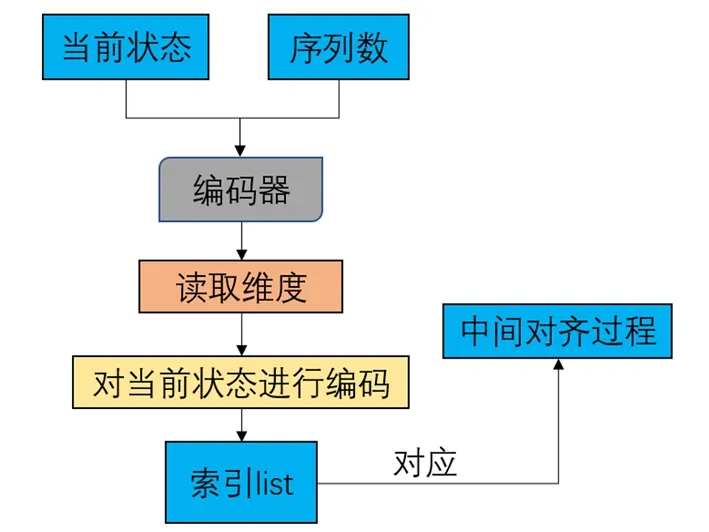
图6 新的中间过程索引计算流程图Fig.6 Calculation flow chart of new intermediate process index
3 实验
3.1 数据集
使用的数据集信息见表1,本次实验采用Homfam中的CBD3蛋白质数据集,为了验证网络在不同序列数量的表现情况,分别抽取了CBD3中的前12条、前15条、前20条、前24条、前50条、前100条的序列分别进行实验,通过不同数量序列的对齐结果来验证提出方法的有效性.从MSADRL的实验数据集中,本次实验抽取了o1—oxbench—414数据集来探究长度敏感随机探索策略对于网络的贡献程度,为了丰富o1—oxbench—414数据集中的数据,使用o1—oxbench—414的近亲数据集对o1—oxbench—414数据集进行一定程度的填充再进行实验.
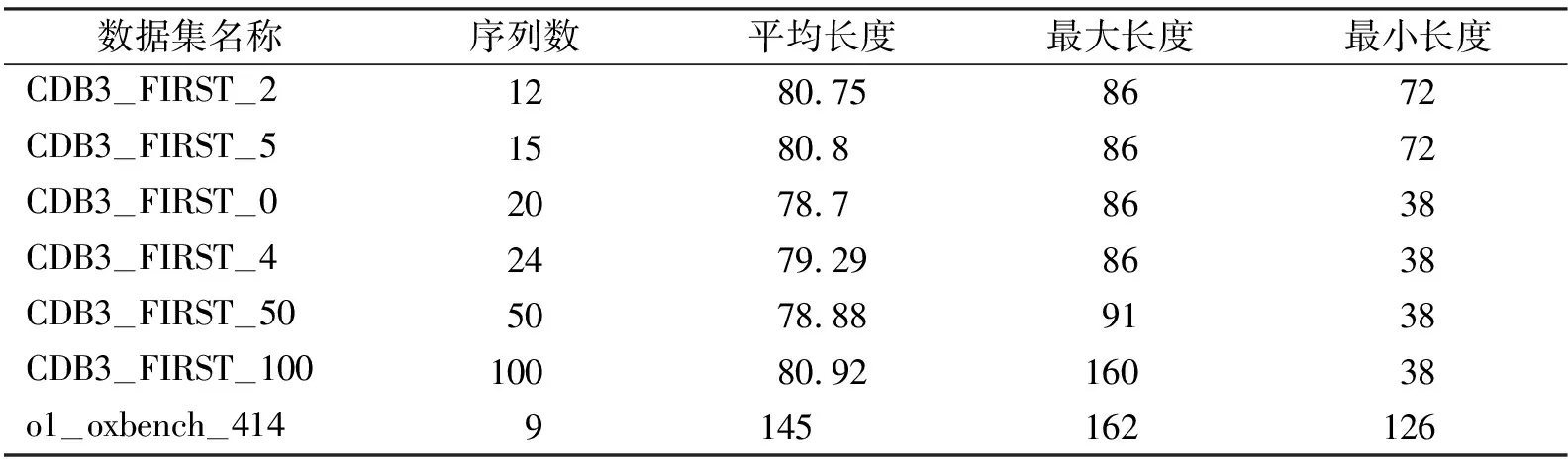
表1 数据集信息表Tab.1 Dataset information table
3.2 评价方式
本次的评价方式采用SP分数进行评价,评价序列对齐结果的SP分数定义如式2所示:
(2)
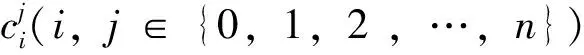
3.3 实验过程
本次实验使用6个数据集来比较CDRL和MSADRL及其不同变种之间的差距.为了验证提出的2个改进策略的有效性,本次实验使用长度敏感MSADRL、动作指导MSADRL以及2种改进策略都加入的MSADRL进行实验(所有方法都使用中间过程索引).随后,本次实验对CDRL和MSADRL在网络参数量上进行了比较,证明了提出的方法成功将网络的空间复杂度从现有方法的O(n2)降低到O(n),使得网络的参数量与序列数量呈线性关系.
3.4 实验结果
本节将展示和分析2个对比实验结果,第一个实验使用6个不同数据集,第二个实验将第一层网络参数量以及网络总参数量进行对比.
3.4.1 SP分数对比实验
将CDRL和其他方法在6个不同序列数量数据集的实验结果进行对比,其中SP分数的对比实验结果如表2所示.从表2可知相对于其他强化学习MSA,CDRL表现最为优异,其SP分数都高于其他模型.第一,因为CDRL的上下文信息包含了与当前状态更加贴近的信息,这使得网络更加容易从历史经验中学习到有用的信息.第二,CDRL的网络收敛速度快,这归功于其输入参数少于其他模型,网络总体的探索量也相应减少.因此,在探索次数相同时,CDRL可以学习到更为出色的策略,从而提高其性能.
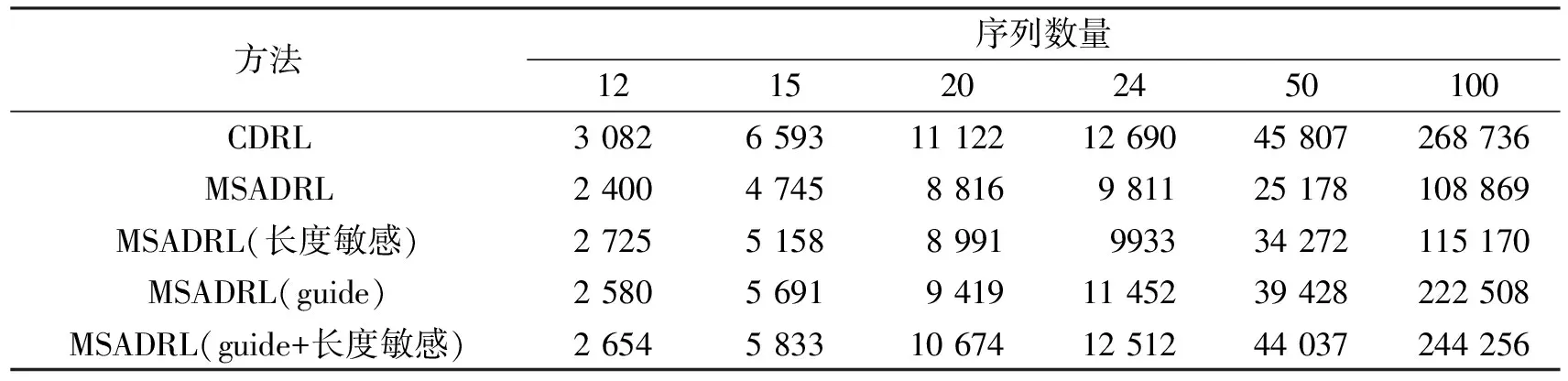
表2 SP分数结果对比表Tab.2 The table of SP score comparison results
相较于业界当前的MSADRL,加入动作选择指导策略后的MSADRL表现更加出色,因为MSADRL在有限轮次内无法实现收敛,以至于智能体无法有效地探索状态空间.指导策略的引入使得网络能够更有效地利用探索过程中获得的经验,从而提高性能表现.指导策略引入了额外的知识和先验信息,能帮助网络准确地预测状态和动作的价值或概率,从而使得网络能够快速地收敛.
长度敏感随机探索策略的加入也可以提高模型的表现,因为长度敏感随机探索策略有类似注意力机制的作用,让网络在有限的探索次数内更加关心那些对全局影响较大的操作,使得网络能够获得更佳的实验性能.长度敏感随机探索策略的加入还可以减少网络的训练时间,为了探究长度敏感随机探索策略的优势,本次实验对加入长度敏感随机探索策略的MSADRL和原本的MSADRL在o1—oxbench—414数据集的实验结果进行对比,实验结果如表3所示.

表3 长度敏感随机探索策略实验比较表Tab.3 Experiment comparison table of length-sensitive random exploration strategy
从表3的实验结果中知加入长度敏感随机探索策略的MSADRL在性能上和时间上都优于原有的MSADRL,具体体现在SP分数值高和用时少,这证实了长度敏感随机探索策略的有效性.
3.4.2 网络参数量对比实验
本次实验统计了CDRL和MSADRL网络第一层的参数量以及网络总参数量,其中第一层网络参数量的对比结果如表4所示.从表4可知,相对于MSADRL,CDRL有更少的参数量,这是因为本次实验将网络的中间层输出作为上下文,将网络的输入维度由现有方法的O(n2)降为O(n).CDRL的网络第一层的参数量远远少于MSADRL,比如当序列数量为12时,CDRL的参数量比MSADRL少了4.58倍.而随着序列的增加,这个倍数也增大;当序列数量为100时,两者之间相差84.62倍.这证实了CDRL比起MSADRL,更能够克服网络参数过多的问题,即CDRL比起MSADRL而言,更能够胜任较大数据集的任务.

表4 第一层参数量对比表Tab.4 Comparison table of the number of parameters in the first layer
本次实验同样对CDRL和MSADRL方法整个网络的参数量进行了统计和对比.CDRL在总参数量上也有显著的优势,具体的实验结果如表5所示.

表5 总参数量对比表Tab.5 Comparison table of the total number of parameters
类似于表4的第一层网络参数量,从表5的实验结果可知,CDRL的总参数量也比MSADRL少得多,而且随着序列数量的增加,两者之间的差值也逐步拉大.当只有12条序列时,MSADRL有4 988个参数,CDRL有1 660个参数,两者相差3倍;在100条序列的情况下,CDRL只有5 972个参数,而MSADRL则拥有319 060个参数,两者相差50多倍.随着序列数量的增加,MSADRL的总参数量呈现膨胀的趋势,这将无法应对较大数据量,相较而言,CDRL对于较大样本数据集就有其自身的优势,不会出现参数膨胀现象.
3.5 讨论
MSA问题是生物信息学中一个非常重要的研究领域,通过对序列进行比对,可以揭示序列之间的相似性和差异性,从而揭示序列中的隐藏信息.在MSA问题中,强化学习方法表现出了优异的性能,但以往的研究往往局限于小数据集的实验,在处理大数据集时仍然是一个挑战.为了解决这一问题,本文提出了一个新的强化学习MSA框架CDRL,其能够有效地处理较大规模数据集.与以往方法不同的是,CDRL针对输入维度巨大的问题进行了改进,使得网络参数量与序列数量呈线性关系,相比于业界现有方法的O(n2),CDRL规避了参数膨胀现象,从而有可能适用于处理较大数据集.
实验结果表明,CDRL不仅在性能上有显著提升,而且在较大数据集上的处理速度也有明显改善.一是因为网络更好地学习了上下文信息;二是因为长度敏感随机探索策略能够减少学习时间;三是本次实验将网络的中间层输出作为序列的上下文,从而提高了MSA的准确性.
当前强化学习MSA的另一个大难题是学习速度慢.因为目前业界各种方法的智能体需要探索的状态空间大小为nn.CDRL的空间是动态的,不需要为未出现的情况预留空间,这节省了大量不会被使用到但是却预留的空间.还有CDRL采取的长度敏感随机探索策略能够减少学习时间,该策略使得网络更加关注前几条序列(大概率随机探索),这样的做法能够在有限的探索次数内寻找到更多有意义的空间,加快收敛速度.
针对强化学习MSA问题,本次实验在性能上、空间复杂度和网络收敛速度上都进行改进并取得了一定的效果.使得强化学习MSA有可能适用于较大数据集.但是,目前智能体需要探索的状态空间大小仍然为nn,CDRL只能将探索空间往有意义的方向引导,从而得到较优解,但是不能保证本文的方案是最优解.要得到全局的最优解,可能需要引入量子计算去穷尽全局所有nn空间,CDRL为强化学习MSA提供了一种新的思路和可能的解决方案.
4 结论
第一,针对现有强化学习MSA网络空间复杂度过大的问题,提出了新的输入编码方式,将空间复杂度从现有方法的O(n2)降低到O(n).
第二,加快了网络收敛速度,CDRL加入了动作指导策略,来防止网络执行非法操作,即选择之前已选择过的动作.这种策略使得网络每次探索都能完成完整轨迹,即所有序列都探索一遍,避免无效探索,这样加速了网络的收敛.
第三,提高了网络性能表现,CDRL的性能(SP分数指标)是5种方法中最优的(见表2).使用长度敏感随机探索策略让网络在有限的探索次数内更加专注于对全局影响较大的操作,把网络向有意义的方向引导,在加速网络收敛的同时也提高了其性能表现.
第四,打破了现有序列数量的限制,现有强化学习MSA对输入序列数量有限制,比如第一个关于这个方面的研究最多仅使用12条序列[34],其与MSADRL主要使用的数据集一样[35].提出的CDRL当前能运行在100条序列上.CDRL引入了一个新的中间过程索引计算方式,其动态地给中间对齐结果分配索引,不需要预留大量未出现对齐的存储空间,使得空间要求降低,网络能够训练较大规模的数据集.
实验结果表明,CDRL极大地降低了空间复杂度,减少了网络参数,加快了网络收敛速度,提升了实验性能指标,并使其有可能被应用于较大的数据集.然而,强化学习MSA的训练时间仍然较长,模型性能还有待提升.在后续工作中,可以考虑结合遗传算法,以保留经验池中较优的策略并舍弃较差的策略,使智能体能够倾向于更优秀的策略,在相同探索次数内获得更好的训练效果.
本文代码地址:https:∥github.com/ASKJDKASJDK/CDRL.

