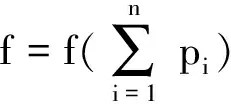Drazin谱及其交换摄动

吴珍莺，曾清平

(1.福建师范大学数学与信息学院，福建 福州 350117；2.福建农林大学计算机与信息学院，福建 福州 350002；3.福建农林大学应用数学研究所，福建 福州 350002)

称代数A是半单的，如果A的Jacobson根rad(A)={0}.本文中，总假设A是半单，有单位元1 的复Banach代数.非零幂等元e∈A称为极小幂等元，如果eAe是可除代数.称A的非零左(右)理想J是极小左(右)理想，如果包含于J中的非零左(右)理想仅有J本身.极小左(右)理想与极小幂等元密切相关：J是A的极小左(右)理想当且仅当存在极小幂等元e使得J=Ae(J=eA)(见文[1，第Ⅳ章，第30 节，命题6]).

定义1设代数A有极小左(右)理想.则A的左(右)基座(socle)定义为包含所有极小左(右)理想的最小左(右)理想.当A有极小左(右)理想，且其左基座等于右基座时，则将A的左(右)基座称为A的基座，记为soc(A).

由文[1，Bonsall-Duncan，第Ⅳ章，第30节，命题10]，当A是半单且有极小左理想时，soc(A)总存在.当A是半单但无极小左理想时，则记soc(A)={0}.复Banach空间X上的全体有界线性算子构成的Banach代数记为B(X)，X上的有限秩算子全体构成的理想记为F(X).众所周知，B(X)是半单Banach代数，且soc(B(X))=F(X)，见文[2，例5.9].

称a∈A是Drazin可逆的，如果存在b∈A和k∈N使得

bab=b，ab=ba且akba=ak.

这时，b称为a的Drazin逆.如果a的Drazin逆存在，则它是唯一的，且属于a的二重换位子.满足上述式子成立的最小的非负整数k称为a的Drazin指标.对a∈A，定义a的Drazin谱为

σD(a)∶={λ∈C：a-λ不是Drazin可逆的}.

对T∈B(X)，ker(T)和ran(T)分别表示T的零空间和值域.T的升指数和降指数分别定义为

asc(T)=inf{n∈N：ker(Tn)=ker(Tn+1)}

和

des(T)=inf{n∈N：ran(Tn)=ran(Tn+1)}.

T的升指数谱和降指数谱分别定义为

σasc(T)∶={λ∈C：asc(T-λ)=∞}和σdes(T)∶={λ∈C：des(T-λ)=∞}.

众所周知，T是Drazin可逆当且仅当asc(T)<∞且des(T)<∞，即σD(T)=σasc(T)∪σdes(T)，见文[3，定理3].

本文的主要目的是通过Drazin谱的交换摄动不变性给出如下元素类

F∶={f∈A：存在n∈N使得fn∈soc(A)}

的内在刻画.具体地，证明了Drazin谱在交换摄动f∈F下是不变的，并且这种摄动不变性刻画了这类元素.这类研究可以追溯到1972年Kaashoek等[4]的一个早期经典结果.当A=B(X)时，证明了降指数谱在交换摄动F∈F下是不变的，且猜想这种摄动不变性刻画了这类算子.直至2006年，Burgos等[5]才给出这个猜想的肯定回答.随后，这一结果被推广到各种谱上.特别地，曾清平等[6]利用拓扑一致降指数理论将这一结果推广到Drazin谱等.Haïly等[7]将文[5]的主要结果从算子情形推广到半单Banach代数情形.本文则将文[6] 中关于Drazin谱的结果从算子情形推广至半单Banach代数情形.

引理1设a，b∈A，ab=ba，且b是幂零元，则

σD(a)=σD(a+b).

证明 仅需证明当a为Drazin可逆时，a+b也是Drazin可逆.若a为Drazin可逆，则由文[3，定理4]，La是Darzin可逆算子，其中La是左乘算子，即Lax=ax，对所有的x∈A.因此，La的升指数和降指数都有限.注意到Lb是与La可交换的幂零算子，由文[4，定理2.2]，La+b=La+Lb的升指数和降指数也都有限.从而La+b是Darzin可逆算子.再由文[3，定理4]，a+b为Drazin 可逆.

设p∈A是幂等元.显然pAp是A的闭子代数，且有单位元p.对b∈pAp，为避免混淆，记

σD(b，A)={λ∈C：b-λ在A中不是Drazin可逆}

和

σD(b，pAp)={λ∈C：b-λp在pAp中不是Drazin可逆}.

当不会引起混淆时，对a∈A，仍记σD(a，A)为σD(a).

引理2设a，p∈A，ap=pa，且p是幂等元，则

(1)σD(ap，pAp)=σD(ap，A)；

(2)σD(a，A)=σD(ap，A)∪σD(a(1-p)，A).

证明 (1)假设λ∉σD(ap，A).则存在b∈A使得(ap-λ)b=b(ap-λ)，b(ap-λ)b=b且

(ap-λ)b(ap-λ)-(ap-λ)是幂零元.

易证pbp是(ap-λp)在pAp中的Drazin逆，即λ∉σD(ap，pAp).反之，假设λ∉σD(ap，pAp).则存在b=pbp∈pAp和正整数k∈N使得(ap-λp)b=b(ap-λp)，

b(ap-λp)b=b且 (ap-λp)kb(ap-λp)=(ap-λp)k.

显然，当λ=0时，b是ap在A中的Drazin逆.当λ≠0时，令q=1-p，注意到ap-λ=ap-λp-λq，那么

且

因此，λ∉σD(ap，A).

(2)由(1)，只要证明

σD(a，A)=σD(ap，pAp)∪σD(aq，qAq)，

其中q=1-p.假设λ∉σD(a，A)，则(a-λ)在A中有Drazin逆b.注意到bp=pb和bq=qb，容易验证pbp和qbq分别是(ap-λp)和(aq-λq))在pAp和qAq中的Drazin逆.从而λ∉σD(ap，pAp)∪σD(aq，qAq).反之，若λ∉σD(ap，pAp)∪σD(aq，qAq)，则(ap-λp)和(aq-λq)在pAp和qAq中有Drazin逆b和c.从而

(a-λ)(b+c)=(b+c)(a-λ)，

(b+c)(a-λ)(b+c)=(b+c)

和

(a-λ)k(b+c)(a-λ)=(a-λ)k，

其中，k是某个不小于(ap-λp)和(aq-λq)的Drazin指标的整数.因此，λ∉σD(a，A).

若存在多项式p使得p(a)=0，则称a∈A是代数元.

定理1设a，f∈A，af=fa，且存在n∈N使得fn∈soc(A)，则σD(a+f)=σD(a).

证明 由于fn∈soc(A)，根据文[2]，fn是代数元，从而f也是代数元.所以，存在多项式h使得h(f)=0，不妨假设h(λ)=λkg(λ)，对某个正整数k和某个多项式g使得g(0)≠ 0.因此，存在多项式q1和q2使得

fkq1(f)+g(f)q2(f)=1.

从而，p∶=fkq1(f)和q∶=g(f)q2(f)都是与f可交换的幂等元.进一步，(f(1-p))k=fk(1-p)=fkg(f)q2(f)=0.注意到g(f)p=0且g(0)≠ 0.令g(0)=μ且m(λ)=g(λ)-μ.由于m(0)=0，可以假设m(λ)=λφ(λ)，对某个正整数l和某个多项式φ使得φ(0)≠ 0.从而，m(f)p=g(f)p-μp=-μp，所以φ(f)fp=-μp.因此，[φ(f)fl-1]nfnp=-μnp，这意味着p∈soc(A).从而(a+f)p∈soc(A)，因此由文[2，推论5.22]知，(a+f)p是代数元.由文[8，定理2.1]知，σD((a+f)p，A)=Ø.同理，σD(ap，A)=Ø.因为a+f与p可交换，由引理2(2)，

σD(a+f)=σD((a+f)p，A)∪σD((a+f)(1-p)，A)=σD((a+f)(1-p)，A).

(1)

因为f(1-p)是与a(1-p)可交换的幂零元，由引理1，

σD((a+f)(1-p)，A)=σD(a(1-p)，A).

(2)

又因为p是与a可交换的幂等元，由引理2(2)，

σD(a)=σD(ap，A)∪σD(a(1-p)，A)=σD(a(1-p)，A).

(3)

由式(1)-式(3)知，σD(a+f)=σD(a).

定理2设f∈A，以下陈述等价：

(i)存在n∈N使得fn∈soc(A)；

(ii)σD(a+f)=σD(a)，对每个与f可交换的元素a∈A.

证明 (i)⟹(ii) 见定理1.

往证：当λi≠ 0时，dimpiApi<∞.若不然，存在λ∶=λi≠ 0及p∶=pi使得dimpAp=∞.由文[7，定理2.3]，在半单Banach代数pAp中存在与fp可交换的非代数元b.显然，b与f可交换，且由文[8，定理2.1]，

σD(b，pAp)≠ Ø.

由假设(ii)，

σD(b，A)=σD(b+f，A).

由引理2(2)，

σD(b+f，A)=σD(b+fp，A)∪σD(f(1-p)，A).

因为(f-λ)p幂零，由引理1，

σD(b+fp，A)=σD(b+λp，A).

由引理2(1),

λ+σD(b，pAp)=σD(λp+b，pAp)=

σD(λp+b，A)⊆σD(b，A)=σD(b，pAp).

这与λ≠ 0和σD(b，pAp)是有界的，矛盾.