基于ARIMA 模型的载人航天器氧分压分析及预测方法

张 震， 胡 伟∗， 郑为阁， 张 莹， 张立红， 鲍军鹏

（1.中国航天员科研训练中心， 北京 100094； 2.西安交通大学计算机科学与技术学院， 西安 710049）

1 引言

载人航天器环境控制与生命保障系统（Environmental Control and Life Support System，ECLSS）简称环控生保系统，为航天员在轨飞行提供大气压力、氧气等必要的生存条件，并对航天器内温度、湿度、有害气体成分等进行控制，以保障航天员生命安全与身体健康，支持航天任务的顺利实施［1-3］。 稳定可靠的环控生保系统对圆满完成载人航天任务至关重要。 地面控制中心对系统运行状态的监测主要依赖于接收到的载人航天器遥测信息，并基于此掌握航天器内部大气压力、氧分压、CO2分压、温度、湿度等环境信息及环控生保系统运行状态，及时发现故障异常并采取应对措施。

载人航天器远离地面，维修成本高、周期长，对系统的可靠性、安全性要求高，在轨运行期间出现的异常状况要求能够快速识别并加以排除。 然而地面工作人员获取航天器信息的来源相对单一，以测控系统接收的各类遥测信息为主要组成部分，对遥测数据进行处理分析以期及时发现、预测故障状态。 其中，作为航天器最具载人特点的关键组成部分环控生保系统，对其遥测数据的分析研究仍需进一步深入［2，4］。 潘点飞等［4］结合环控生保系统遥测数据的特点，通过Akaike Information Criterion （AIC）和Bayesian Information Criterion （BIC）相结合的方法确定预测模型，对未来数据的变化进行了有效预测，然而预测的时间序列数据长度仅为所分析历史数据的6.7%，有效预测时长尚有拓展空间。

航天器遥测数据是典型的时间序列数据。 近年来，自回归移动平均模型（Autoregressive Moving Average，ARMA）和差分自回归移动平均模型（Autoregressive Integrated Moving Average， ARIMA）在各领域的时间序列数据处理、分析、预测中有广泛应用［5］。 朱丽莎等［6］提出了一种动态ARMA 建模方法用于卫星遥测数据建模与预测，提高了建模精度与预测精度。 张瑞国等［7］将ARIMA 模型应用于雷达数据随机误差建模与补偿，有效降低了雷达测量数据随机误差。 Besteiro等［8］提出了应用ARIMA 模型对动物生活区进行分析建模的方法。 谷建伟等［9］将ARIMA 模型与Kalman 滤波方法相结合，能够排除非同步性及滞后性的影响，使识别出的油井产量时间序列模型具有精准的拟合结果和预测能力。 Chen 等［10］将ARIMA 模型与LSTM 模型相结合，对卫星遥测数据进行分析预测。

在短时历史数据基础上分析建模，对未来时间序列数据进行有效预测，不需依赖大量历史数据，有利于对载人航天器内部环境的实时预测。本文针对载人航天器物资消耗型环控生保系统氧分压分析及预测，提出了基于ARIMA 模型的遥测数据分解建模方法，用于分析预测在轨时间序列遥测数据。

2 基于ARIMA 模型的预测方法

2.1 ARIMA 模型基本原理

ARIMA 模型［11］运用差分方法将非平稳时间序列数据转换为平稳时间序列数据，而后依据时间序列数据的平稳性及模型参数对未来数据进行预测。 ARIMA 模型由三部分组成：自回归过程（AR）、差分过程（I）、移动平均过程（MA）。 时间序列数据的差分过程见式（1）～（3）。

式中，ut代表白噪声序列，δ为常数项。 此模型中p为自回归部分的阶数，q为移动平均部分的阶数。 上述模型记为ARIMA（p，d，q），利用滞后算子多项式Φp（L） 和Θq（L）， 式（4）可改写为式（5）～（7）。

ARIMA 模型表征的是时序过程当前状态与历史状态间的关系，其中p阶自回归过程表征的是状态本身的滞后影响及其权重，q阶移动平均过程表征的是时序过程中当前及历史噪声的影响及其权重。

根据ARIMA 模型基本原理，可将非平稳时间序列数据通过差分运算转换为平稳时间序列数据，再根据平稳性的特点，通过对历史数据的提炼分析，得到适于表达系统运行特点的模型，并基于此对系统未来运行状态的有效预测。

2.2 基于ARIMA 模型的数据建模预测方法

首先对待分析数据进行预处理及分解，并对其中的趋势部分进行平稳性检验。 若为非平稳时间序列数据，则需利用差分运算转换为平稳数据。而后对转换后的平稳数据进行模型建模，并基于此生成对原始数据的拟合。 若拟合数据与原始数据间的误差满足要求，则说明估计模型能够有效表达系统运行特点，可据此对系统未来运行状态进行预测。 具体方法流程如图1 所示。

由于数据中偶有缺失、跳变等异常情况，需要对原始数据进行必要的预处理，通过插值，过滤异常点等方法为后续分析计算提供可靠数据源，而后对数据进行成分分解。

时间序列数据xt按组成成分特性不同可分解为趋势性数据tt、周期性数据ct、残差数据rt三部分，按分解方式的不同又有加性模型、乘性模型和混合模型3 种模型表达形式，见式（8） ～（10）。

载人航天器内部环境遥测数据特点以加性模型为主，在实际应用中采用加性模型进行分解。通常周期性数据ct和残差数据rt特性不随时间变化而变化，视为稳定的组成成分，而趋势性数据tt需进一步进行平稳性检验。 若为平稳数据，则可对其进行数据建模；若为非平稳数据，则需采取差分运算将其转换为平稳数据。 在进行平稳性检验时采用ADF 单位根检验法［12］。

在对平稳化处理后的趋势性数据进行ARIMA 建模时，需要确定模型的参数。 本文主要采用自相关函数和偏自相关函数图形法［10］对ARIMA 模型的参数进行确定。 之后基于构建完成的ARIMA 模型，生成趋势性数据的拟合t＾t， 并叠加周期性数据估计c＾t， 可实现对原始时间序列数据的拟合。 拟合结果可用如式（11）所示的均方根误差（RMSE）来表征。

其中，N为数据样本量。

鸡翅又名鸡翼、大转弯，肉少、皮富胶质，是整个鸡身最为鲜嫩可口的部位之一，分翅尖、翅中和翅跟三个部分。翅中，肉多、胶原蛋白含量丰富，肉质细嫩多汁，味道鲜美，具有低脂肪、高蛋白、低胆固醇、易烹饪等特点，而且富含人体所必需的磷、铁、钙及VB1、VB2和尼克酸等营养元素[1，2]。

若RMSE 较小，则说明模型对原始数据的拟合效果较好，可以据此对系统未来运行状态进行预测。 若RMSE 较大，则说明原始数据分解建模过程中存在可优化的地方，需反复进行迭代优化，直至达到预期效果。

3 试验验证

载人航天器在轨运行期间的氧分压是航天员赖以生存的基本条件，对其进行实时监测并合理预测趋势走向，对于及时发现环控生保系统问题隐患，保障航天员生命安全和身体健康具有重要意义。 本文选取氧分压信息进行分析建模，并以此为示例展示本文方法应用的详细过程。

试验选取某载人航天器在轨运行期间氧分压信息，1 h 进行1 次采样，共取采样点数300 个。按照分析建模数据与预测测试数据约3 ∶1 的比例进行划分，其中前228 个采样点作为原始数据进行分析建模，后72 个采样点作为测试数据用于对预测效果进行评估。

3.1 数据分解

图2 为氧分压原始时间序列数据。 从图中可知，氧分压的原始数据具有很强的周期性和趋势性，对其进行进一步分解可得到趋势部分、周期部分和残差部分数据，如图3 所示。

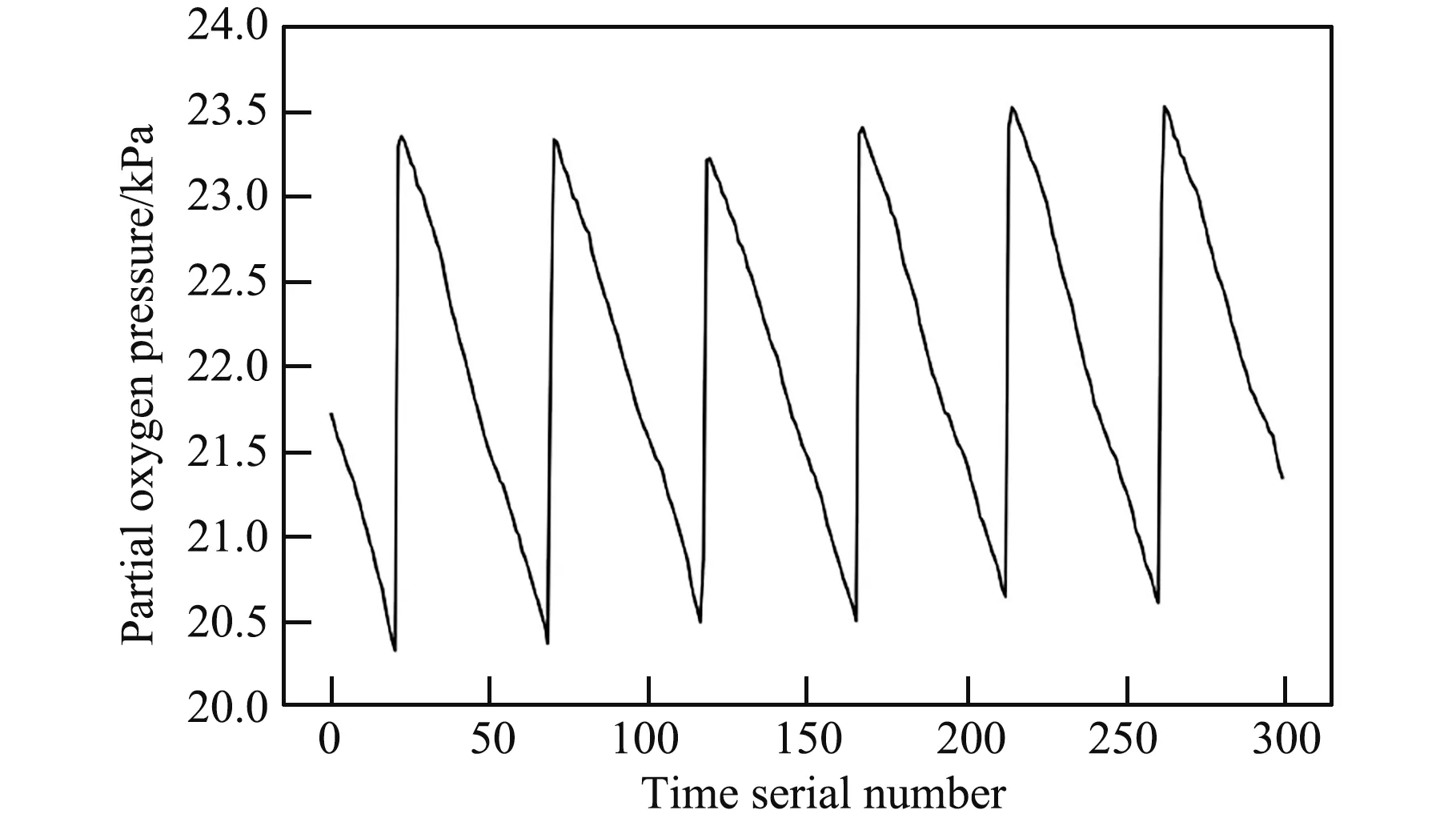
图2 氧分压原始时间序列数据Fig.2 Time serial data of original partial oxygen pressure

从图可知，趋势部分数据有明确的趋势变化，是非平稳数据，而残差部分数据虽有少量点位出现了明显跳变，但整体仍具有平稳性且多数在零点附近波动幅度较小，对数据整体变化趋势影响不大。 在对图形进行初步分析的基础上，对趋势部分数据和残差部分数据分别进行ADF 检验，如表1 所示。

表1 趋势及残差数据ADF 检验结果Table 1 ADF test results of trend and residual data

从ADF 检验的结果可知，针对趋势数据，其ADF 值大于10%显著水平，显示序列为非平稳序列。 而残差序列ADF 值小于1%显著水平，且P值远小于0.01，显示其为平稳序列，与图形分析结果吻合。 图4 显示的是残差数据的ACF 图和PACF 图，从图中可以看出2 个函数的一阶运算结果已经在置信区间中，说明序列本身不存在相关性，进一步证明了残差序列可视为随机序列。

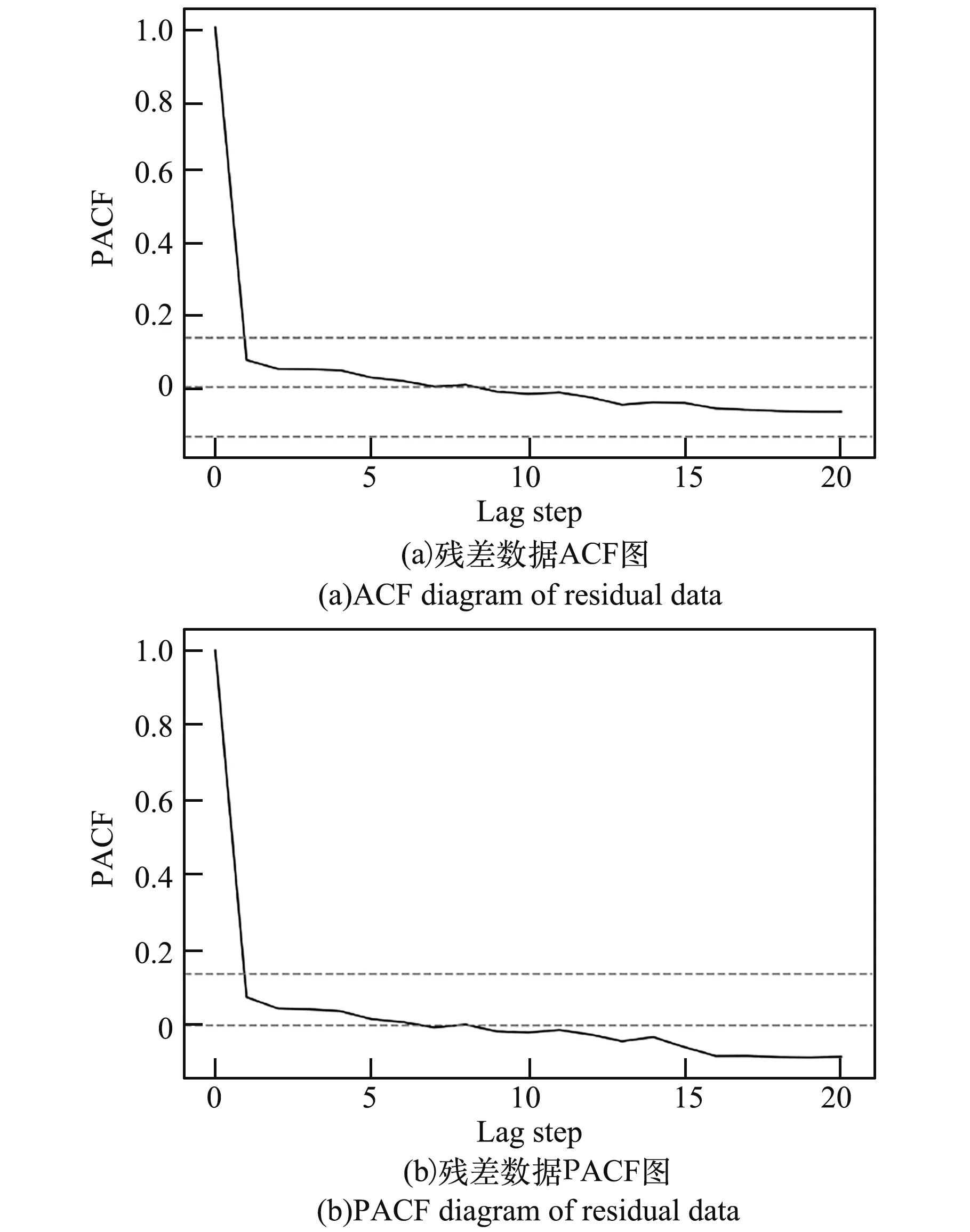
图4 残差序列ACF 和PACF 图Fig.4 ACF and PACF diagrams of residual data

3.2 趋势性数据建模

从上节的分析可知，氧分压原始数据分解出来的趋势数据成分具有非平稳性的特点，需要进一步分析。 首先对其进行一阶差分平稳化处理，并进行ADF 检验，结果如表2 所示。

表2 趋势差分数据ADF 检验结果Table 2 ADF test results of differential trend data

从ADF 检验结果可知，经过一阶差分后，趋势差分数据的ADF 值小于1%显著水平，P值小于0.01，说明此时数据序列已可视为具有平稳性，可对其进行建模分析。 因采取了一阶差分运算对氧分压时间序列数据的趋势部分进行了平稳化，可知ARIMA（p，d，q）模型中的参数d＝1。 参数p和q的确定需使用ACF 和PACF 图形法。 对趋势差分数据绘制ACF 图及PACF 图如图5 所示。

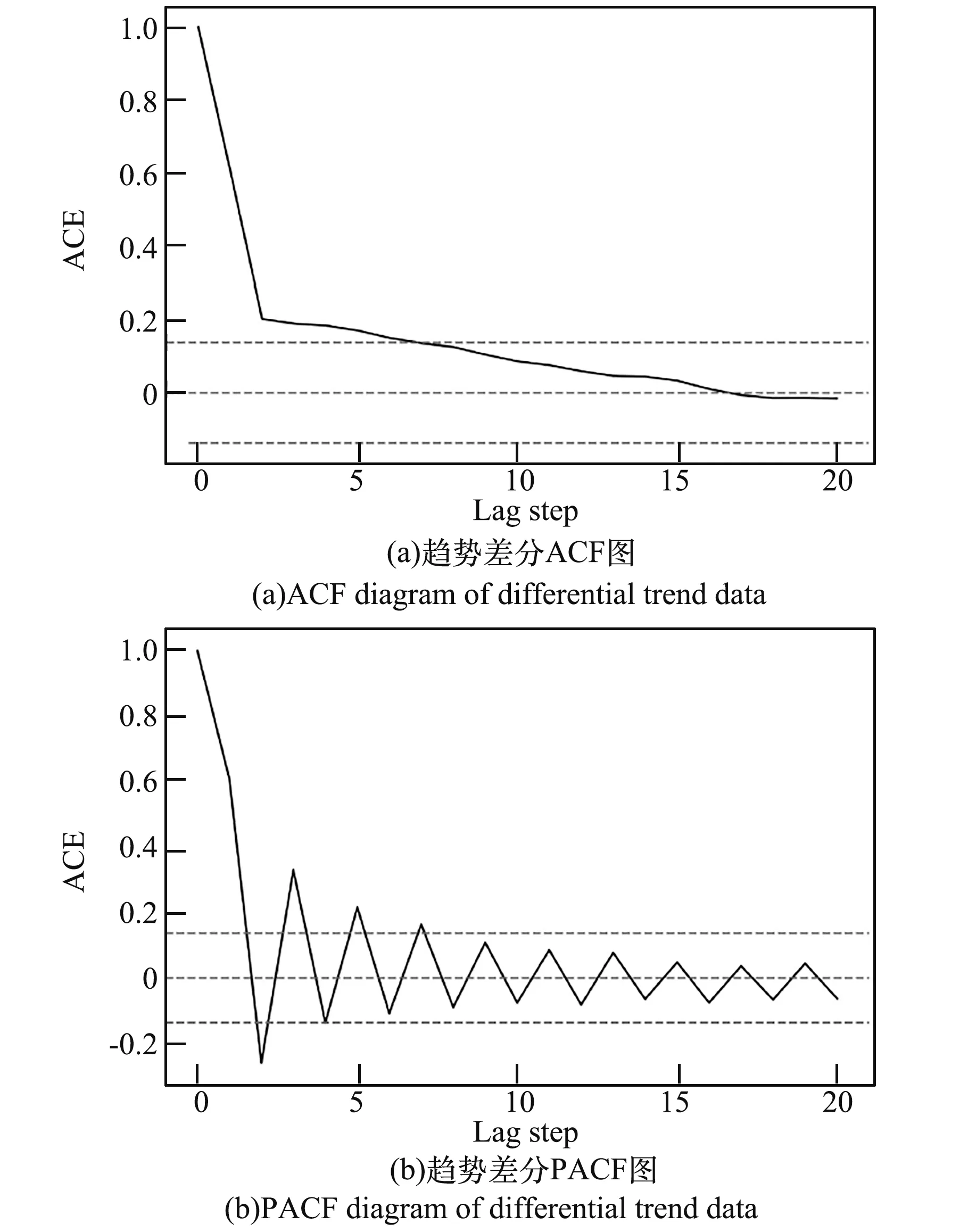
图5 趋势差分序列ACF 和PACF 图Fig.5 ACF and PACF diagrams of differential trend data

从图中可见，ACF 曲线在2 阶后衰减趋于0，PACF 曲线在1 阶后震荡趋于0，可初步确定参数p＝1 和q＝2。 依据AIC 准则［4］判断上述参数是否为最优滞后阶数，计算AIC 统计结果如表3所示。

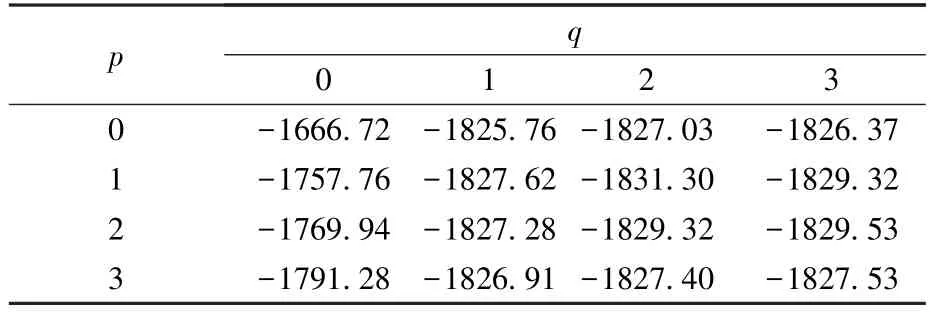
表3 AIC 统计结果Table 3 AIC statistics results

从表中可知，当p＝1 和q＝2 时，AIC 统计值最小，从而验证了取值合理性。 综上所述，ARIMA（1， 1， 2）为最优模型。

3.3 模型拟合及预测

基于上述方法得到的ARIMA 模型，进行氧分压趋势部分数据拟合并叠加前期分解出的周期部分数据，得到对在轨氧分压遥测数据的拟合数据，图6 是原始数据与拟合数据的比对情况。

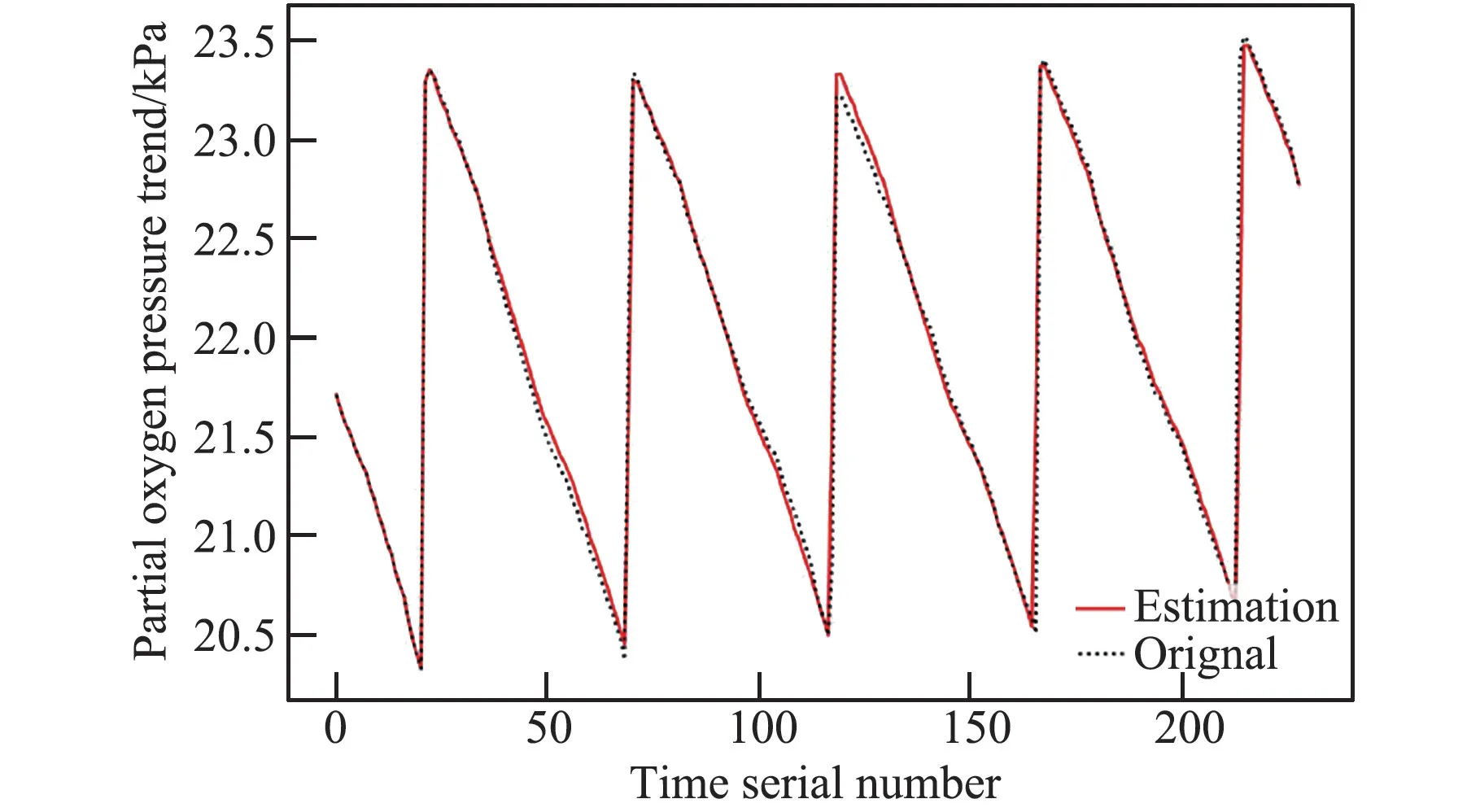
图6 氧分压原始数据与估计数据对比图Fig.6 Comparison of original and estimated partial oxygen pressure data

计算出的RMSE为0.1537 kPa，由于采样部分原始数据均值为21.97 kPa，均方根误差与均值的比值为0.0070，估计精度良好。 图7 为氧分压原始数据与预测数据的对比图。

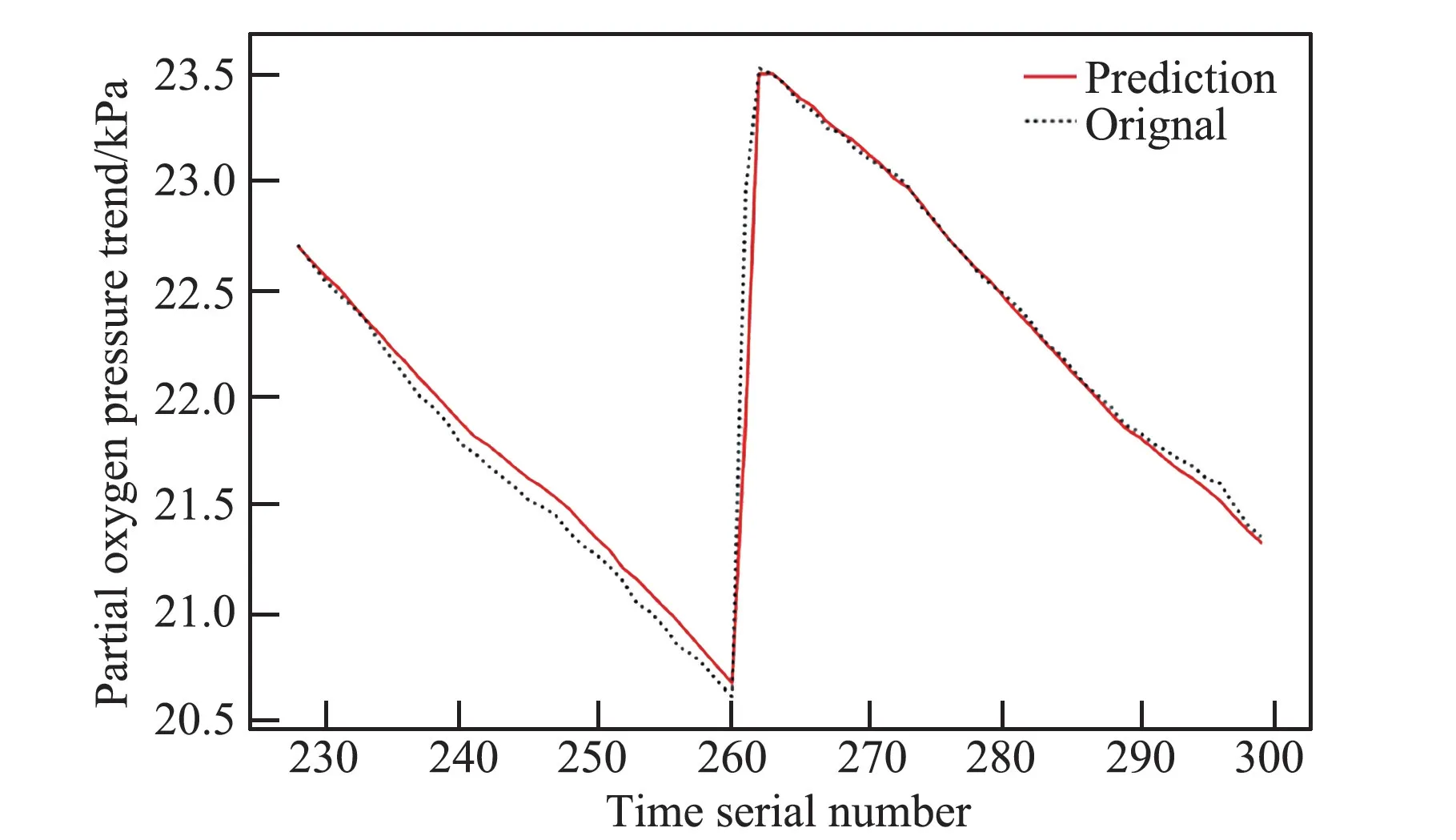
图7 氧分压原始数据与预测数据对比图Fig.7 Comparison of original and predicted partial oxygen pressure data

应用上述模型方法进行预测时，预测出的结果和实际值的偏差能反映算法预测效果，从上图中可看出，预测值与实际值走势一致，预测时间序列数据长度为所分析的历史数据长度的31.6%，有效提升了现有预测方法的预测时长，计算出的RMSE为0.1378 kPa，由于实际数据均值为22.08 kPa，均方根误差与均值的比值为0.0062，预测精度良好。

由于载人航天器内部环境信息时序数据如大气环境压力，CO2分压，温度，湿度等均具有与氧分压相似的加性模型形态，可分为趋势、周期、残差等3 部分，本文方法对其余环境信息遥测数据的分析预测也提供了可行参考。

4 结论

1）针对载人航天器物资消耗型环控生保系统氧分压的分析及预测，提出了基于ARIMA 模型的时间序列数据分解、建模、预测方法，并将其应用于在轨环境信息的分析预测中，以提前识别系统运行过程中的异常状态。

2）将此方法应用于载人航天器内氧分压在轨遥测数据的分析预测，实测结果表明：该方法对原始数据拟合的均方根误差为0.1537 kPa；利用短时数据，可对未来载人航天器内氧分压的变化进行有效预测，有效提升了现有预测方法的预测时长，预测均方根误差为0.1378 kPa，预测精度较高。

3）为推进载人航天器在轨运行状态的精确预测提供了可选方案，可进一步推动地面控制中心的自动化运行，减轻地面监测的工作负荷，避免人为因素对环境信息监测带来的干扰，增强载人航天器在轨运行安全性进行了有益探索。