基于分区模型的液氢贮箱地面温度与压力分布研究

朱洪来， 赵立伟， 梁红义， 魏健健

（1.北京控制工程研究所， 北京 100190； 2.浙江大学制冷与低温研究所， 杭州 310027）

1 引言

为实现更高比冲、更大的运载能力，早期各国的运载火箭应用液氢／液氧低温推进剂，并逐步利用低温火箭末级或上面级开展短期空间飞行任务，成为了低温空间飞行器的雏形。 液氢贮箱工作在空间复杂热环境下，内部压力随工作时间逐渐增加，因此压力控制是液氢贮箱关键技术之一。液氢贮箱面对空间恶劣的热环境，由于空间微重力造成内部介质自然对流消失，加之液氢的热导率低，从而液氢贮箱内出现严重的热分层现象［1］。 热分层直接造成贮箱内部气液两相局部过热，引起液氢非必要气化，从而引起低温贮箱内压力异常变化。

1987 年，波音公司对贮箱内液体由于混合引起的气相液化以及液体消除分层问题进行了实验研究［2］。 1993 年，NASA Levis 研究中心通过数值分析与实验数据对比方法研究了液氢贮箱强制对流去分层问题［3］。 2016 年，NASA GRC 对液氢储罐的蒸发率进行了2 次实验［4］，实验检验热力学排气与流体混合系统在地面液氢试验中抑制气相和液相热分层的能力。 2017 年，Huang 等［5］、Wang 等［6］在室温温区TVS 模拟装置采用R141b为气液相变贮存介质，针对TVS 的混合模式和排气模式提出了3 种运行控制策略，进行了贮箱内液体温度、热分层以及排气损失的研究。

为分析低温贮箱内的流场和温度场的演化规律，多采用计算流体力学（Computational Fluid Dynamics，CFD）通用软件Fluent 或CFX 等进行物理仿真分析开展了数值分析。 Grayson 等［7］基于Fluent 软件开展了一系列液氢贮箱自增压、循环去分层过程的CFD 数值研究。 考虑到箱体的轴对称，数值模型为二维轴对称几何。 两相流动多计算采用体积含量模型（Volume of Fluid，VOF），相比于对气相和液相分别建立Navier-Stokes（NS）控制方程的Euler-Euler 模型，该模型为单流体模型，即假设气液两相流为一种混合流体，只对混合流体（Mixture fluid）建立相应的NS 守恒方程，其中相含量通过一个额外的相体积输送方程计算得到。 由于是单流体方程，控制方程相对Euler-Euler 模型减少，因此计算速度更快，收敛性更好。缺点是该模型假设气液之间没有相对速度，即不考虑相间的相对速度。 但考虑到储罐内流动速度小，因此该假设引起的误差可以忽略。

由于漏热条件等因素影响贮箱的增压速率缓慢，且受时间步长的限制，采用Fluent 软件计算出在给定时间内的温度分布极为困难。 本文采用分区模型，将贮箱内部空间分为过热区、饱和区和过冷区三块区域，离散化气相／液相区质量和能量守恒方程和热力学方程，确定初始条件，求得液氢贮箱内热分层与压力分布。

2 理论分析

2.1 分区模型

液氢贮箱的三区模型示意图如图1 所示，贮箱为椭球封头加圆柱段构型。 贮箱漏热为第二类边界条件的均匀热流密度漏热，其热流密度沿贮箱轴对称。 不考虑由于外界气温和绝热材料不均匀性导致的漏热随时间的变化。

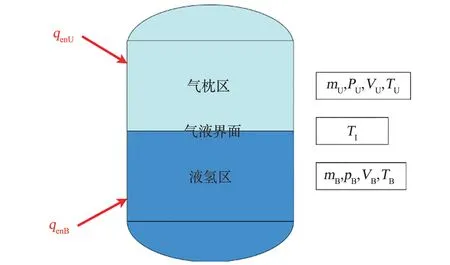
图1 液氢贮箱的三区模型示意图Fig.1 Three zone model of the liquid hydrogen tank

在贮箱内部介质所占空间分为气枕区、气液界面区和液氢区3 块区域，各区分别为一个单独控制体。 基于贮箱和外界环境条件沿贮箱轴向的对称性，气枕区仅在贮箱轴向方向存在较大温度梯度，但无明显压力梯度变化。 由于重力作用，不考虑气枕与贮箱壁面有附着液体。 气液界面区抽象为一层无质量的界面层，分别对气枕区和液氢区进行传热和传质。 贮箱内流动速度小，暂不考虑该气液之间相对速度。

2.2 控制方程

2.2.1 气枕控制体

对于气枕区域，通过质量守恒可得气枕质量变化率为式（1）：

通过能量守恒，可得温度变化率为式（3）：

式中，TU为气枕温度，其为贮箱高度和时间的函数，qenU为环境对气枕区的热流密度，qUI为气枕区对界面的热流密度，pU为气枕区压力，VU为气枕体积，hgsat为饱和气体焓，cvU为气枕区定容比热。

气枕温度为式（4）：

根据理想气体状态方程可知气枕各参数关系为式（5）：

2.2.2 气液界面控制体

气液界面温度TI可以通过修正Alabovskii 方程［8］得式（6）：

式中，K参数随温度变化，可以通过液氢参数表查取。

气液界面气化或冷凝质量可通过等能量阶跃条件［9－10］求得，如式（7）所示。

式中，qIB为界面对液相区的热流密度，hg和hl分别为气氢和液氢的焓值。hg（TI，pU） 和hl（TI，pU） 分别为气氢和液氢在界面温度和气枕压力下的焓值。

2.2.3 液氢控制体

对于液氢区域，通过质量守恒可得式（8）：

液氢质量的初始条件为式（9）：

通过能量守恒可得式（10）：

式中，TB为液体温度，qenB为环境对液体区的热流密度，hl为液体焓，cpB为液氢区定压比热。 液体温度的初始条件为式（11）：

液体体积变化率可以写为式（12）：

式中，ρl为液氢密度。

液体体积的初始条件为式（13）：

2.2.4 补充条件

气枕和液体充满整个贮箱，因此可得式（14）：

式中，VT为贮箱容积。

气枕区冷凝液质量流量可以表示为式（15）：

根据传热学，气枕区对界面的热流密度和界面对液相区的热流密度可以写为式（16）、（17）：

式中，AI为气液交界面面积，kU和kB分别为气相和液相的热传导系数。

2.3 温度与压力分布求解

模型通过REFPROP V9.1 软件可获得给定三区中任一区对应的温度、压力下焓、比热、密度和传热系数等热物理参数，用于方程迭代计算。利用MATLAB 软件可编程求解液氢贮箱内自增压过程曲线、维持时间和内部液位变化。 程序求解的流程图如图2 所示。

图2 求解程序流程图Fig.2 Solver flow chart

3 结果与讨论

3.1 模型验证

本文采用低比表面积的类球体液氢贮箱作为研究对象。 贮箱采用标准2 ∶1 椭球封头，贮箱内径及贮箱总体高度均为2600 mm。 贮箱内液氢初始温度为20 K，外部漏热为第二类边界条件，热流密度为0.83 W／m2。 图3 为20%和80%两种初始充满率下，Fluent 软件和节点法的三区模型计算得到的结果对比。 结果可得，在Fluent 模拟的增压过程的时间内，三区模型与Fluent 的计算结果较为接近，对不同初始充满率下的贮箱的增压计算偏差不超过30 kPa。 因此，可以采用计算速率更快的三区模型来计算得出贮箱的增压曲线。

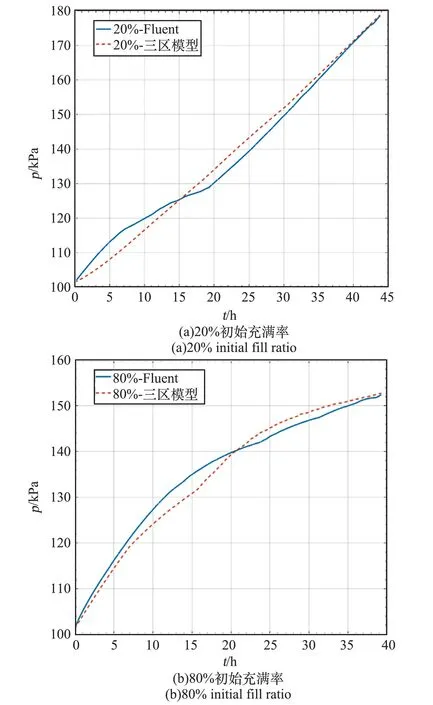
图3 2 种模型的增压Fig.3 Pressure increase by fluent and three zone model

在模型中，气液界面厚度dx应远小于气相区的高度（H－Hgs）。 目前Fluent 计算中，初始充满率80%的算例在气相温度分层上形成近似线性的情况，因此这里采用初始充满率80%在133 875 s 时刻的温度分层数据来作为得出气液界面厚度的参考值。 使用三区模型计算得到133 875 s 时刻的液相区平均温度Tl，气相区平均温度Tg，气相区饱和压力Ps和温度Ts，液位H，计算得出气相区顶部温度Tm，并与Fluent 计算结果进行比较，可得如图4 所示的计算结果。

图4 模型气相区温度分层Fig.4 Temperature stratification by fluent and three zone model

如图4 所示，三区模型的计算结果和Fluent基本符合。 液相区温度相比于Fluent 计算结果在某些高度部分存在0.2 K 左右的偏差。 位于罐底的温度偏差是由于液相区均匀漏热采用的第二类边界条件造成的，位于气液界面处的偏差则是局部传质使得流场温度不均匀导致。 关于气相区的温度分布，Fluent 的计算结果显示，计算时刻其还未发展为线性，因此和线性分布的假设存在偏差。

在图4 的计算中， 气液界面的厚度为27.8 mm，仅为贮箱高度0.5%，符合三区模型中两相区为薄膜的假设。 与文献［11］所提及的氢气与液氢过热度为30 K 的工程经验和液氢贮箱0.83 W／m2的漏热条件，对80%初始充满率的算例，气液界面厚度与贮箱高度比也是基本一致的。

3.2 压力分布

图5 为使用一维节点法的三区模型计算得到的3 种不同初始充满率贮箱内部气相区压力以及贮箱内液位随时间的变化情况。 液位变化显示，20%初始充满率的贮箱变化趋势与60%和80%初始充满率贮箱的情况不同，随时间逐渐减小。 说明低初始充满率情况下液体膨胀速率要低于蒸发速率，而初始充满率高的情况下则反之。 在压力计算方面与图5 的计算结果不同的是，在增压前期（约3 h），80%初始充满率的贮箱增压速率最大，20%的增压速率最小；然而在长期存储（约200 h）中，80%初始充满率的增压速率在三者中为最小，20%初始充满率的增压速率最大。 对于20%、60%和80%初始充注率的工况，自增压到0.5 MPa 所需的时间分别为125 h、240 h 和390 h。

图5 增压曲线和液位变化Fig.5 Pressure increase and level change curve

在初终压以及漏热都相同的情况下，增压速率与所经历的时间呈负相关，经历的时间与不同初始充满率下单位体积的总内能变化量ΔU呈正相关。 因此，从仲氢T-v物性图（图6）中可得，3种不同初始充满率的等比体积线代表贮箱从0.1 MPa 增压至0.5 MPa 的热力过程，而3 条线的初始和终态位置可查询得到增压过程的单位体积内能变化量ΔU。 内能变化量越大，意味着漏热时间越长，即表示增压速率越慢。 从图中可得，80%初始充满率的增压速率最慢，20%初始充满率的增压速率最快。

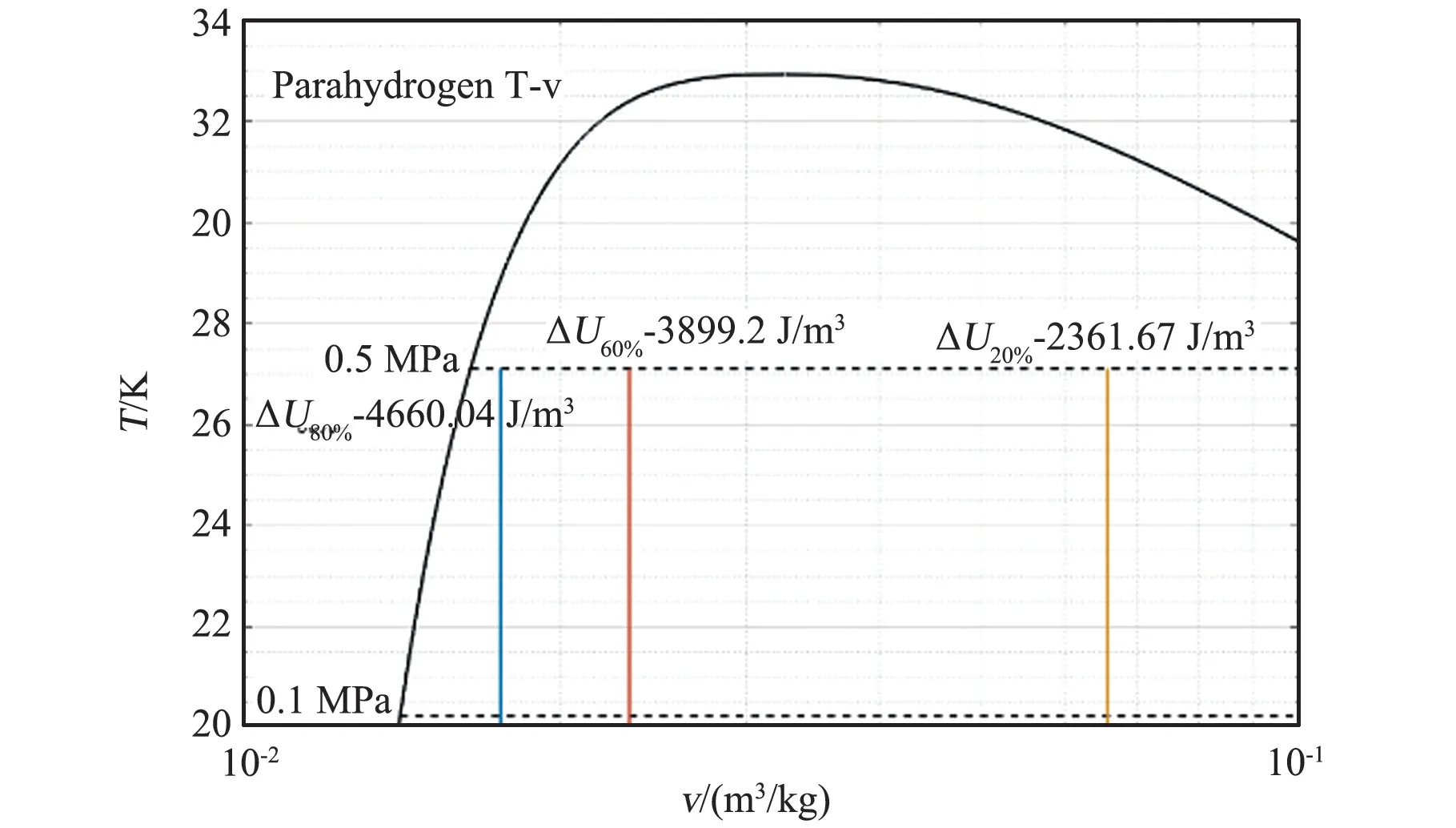
图6 仲氢的T－v 图Fig.6 Para-Hydrogen T-v cure

3.3 温度分布

基于三区模型可计算得出初始充满率分别为20%、60%和80%情况下的温度分布情况，如图7所示。 由于氢的两相物理参数的差异，图中温度分布曲线的转折点出现在气液界面上，转折点前的液相温度梯度明显小于转折点后的气相温度梯度。 相同漏热情况下，填充率越高的气相温度梯度更大。 因此对于加注后未使用的液氢贮箱的温度监控更为重要。

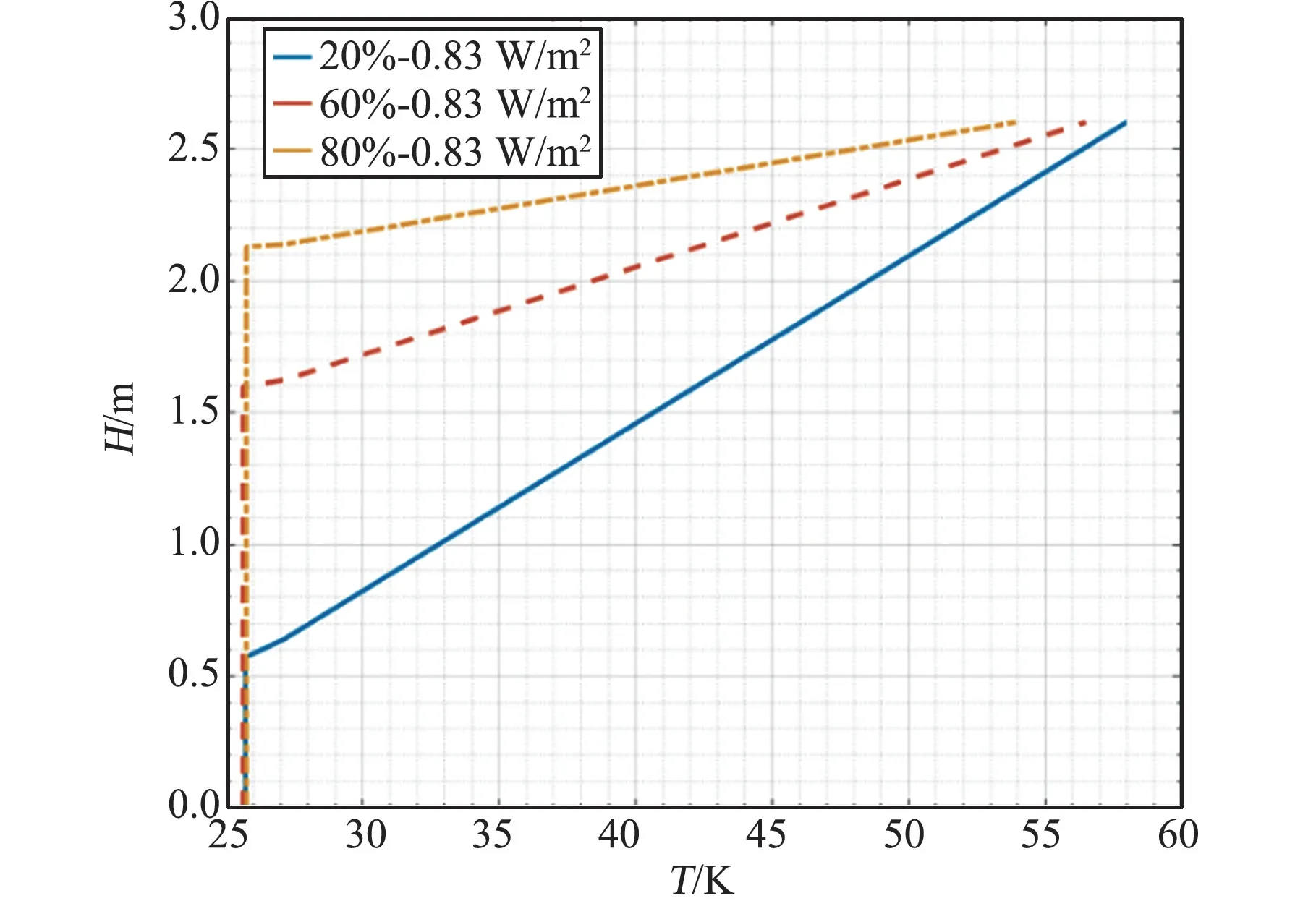
图7 温度分层结果Fig.7 Temperature stratification results

4 结论

采用分区模型可以有效求解地面液氢贮箱内气液两相的温度和压力分布情况，通过分区模型的求解过程可得如下结论：

1）不同初始充满率的贮箱在给定漏热条件下，三区模型对贮箱内的压力和液位进行计算结果与Fluent 的计算结果得到较好一致性；

2）在前人试验和仿真结果基础上建立的基于守恒定律和热力学定理三区模型求解方法，在液氢贮箱内温度与压力分布中保持计算精度条件下，大幅减低求解计算规模；

3） 三区模型可以计算不同填充率下、不同时刻液氢贮箱内温度与压力分布，为贮箱的压力控制和热分层抑制提供了判定依据，同时为后续的热力学排气与流体混合过程提供了初始条件。