空间站转位机构制动动力学特性研究

沈晓鹏， 胡雪平， 刘 艳， 刘永强， 陈超云， 苑会领

（上海宇航系统工程研究所， 上海 201109）

1 引言

中国空间站包括核心舱、实验舱Ⅰ和实验舱Ⅱ3 个舱段，采用水平对称的T 形构型作为空间站三舱组合体基本拓扑结构。 三舱构型采用先对接再转位的方式完成组建，并将转位机构组建作为主份方案［1］。 转位机构选用平面转位机构来实现。 平面转位机构具有2 个旋转自由度，2 个旋转关节轴线平行，制动时2 个关节会发生动力学耦合［2］。

转位机构的转位对象为实验舱，其转动惯量达106kgm2量级，比中国常规飞行器转动惯量高1～2 个数量级。 在实验舱转位到位后转位机构的电机停止转动，但是舱体由于存在大惯性不能马上停止运动，因此需要对舱体进行制动。 舱体制动产生的力矩会反作用于转位机构关节上，过大的反作用冲击将会造成转位机构关节传动链以及结构件破坏，因此转位机构在关节传动链中设置了弹簧阻尼缓冲装置来进行制动。 在理想状态下，平面转位机构模型可以简化为两自由度弹簧阻尼扭振系统，但是实际产品由于传动链摩擦和间隙的存在，使得制动过程呈现出非线性特性。对转位机构制动过程关节特性进行研究，对于转位机构的系统参数和关节性能设计有着重要意义。

近些年来，不少研究人员开展了间隙系统的理论研究。 时培明等［3］建立了旋转机械含间隙强非线性扭振系统的动力学方程，利用数值模拟的方法得到系统在强非线性项参数变化下的分岔行为。 周鹏等［4］建立了干摩擦下含双侧塑性约束的双自由度碰撞振动系统的动力学模型，并利用数值迭代方法求解和分析系统的复杂动力学行为。 张艳龙等［5］研究了在非光滑因素间隙及摩擦作用下的强非线性系统动力学行为，探讨摩擦诱导振动及其他关键参数对系统动力学特性的影响。 Cone 等［6］从一类轴承模型中简化出含间隙及摩擦的单自由度碰撞振动系统，进行动力学分析发现黏着的存在。 师建国等［7］建立了含对称间隙的轧辊横向碰撞振动模型，采用四-五阶Runge-Kutta 法进行了数值求解，研究了轧辊与导板间的非线性振动特性。

本文在以上研究成果的基础上将转位机构制动过程简化为理想的两自由度弹簧阻尼扭振模型，并在理想模型基础上增加了摩擦阻尼和传动间隙因素，得到了更为真实的动力学模型，通过对模型进行动力学响应数值分析，获得了关节的时域动态响应图，分析出摩擦阻尼和传动间隙对转位制动过程的影响，并与试验结果进行对比，以期为转位机构的工程研制提供理论参考。

2 制动过程动力学模型

转位机构是将实验舱Ⅰ和实验舱Ⅱ从核心舱的轴向对接口转位至相应的侧向停泊口。 平面转位机构的转臂安装于实验舱上，主要由肩关节、腕关节、捕获连接机构和臂杆等组成。 核心舱上安装有转位机构基座。 转位前，转臂通过捕获连接机构与基座建立刚性连接。 实验舱的转位过程通过肩关节和腕关节的交替转动来实现。 转位机构组成及布局如图1 所示。

图1 转位机构组成及布局Fig.1 Composition and layout of transfer mechanism

由于转位机构的臂杆结构刚度高于关节刚度2 个数量级，可将臂杆视为刚体。 平面转位机构的肩关节和腕关节回转轴线平行，可以将其简化为肩关节和腕关节两自由度的串联弹簧阻尼扭振模型。 转位机构制动过程简化模型如图2 所示。

图2 转位机构制动过程简化模型Fig.2 Simplified braking model of transfer mechanism

转位过程中核心舱的姿控发动机为关闭状态。 如果核心舱控制力矩陀螺（Control Moment Gyro，CMG）工作，核心舱将由于控制力矩的作用保持姿态不变，仅会产生空间位置的变化。 转位机构制动动力学的研究仅关注关节的角位移响应情况，因此可将受CMG 控制的核心舱视为固定状态（同时约束姿态和位置变化），在不影响关节角位移动态响应结果的情况下可以使问题得以简化。

将不受CMG 控制自由状态的核心舱假定为固定状态来进行动力学等效，则转位过程中实验舱的等效质量只有原质量的1／2 ～1／3［8］。 如果核心舱固定状态下转位实验舱的质量等于原质量大小，则该状态下转位机构制动过程的负载质量大于核心舱自由状态，因此核心舱受控下转位机构制动载荷大于核心舱自由状态，这里选取更恶劣的核心舱受控工况进行制动动力学分析。

将转臂的零部件等效到腕关节处的集中转动惯量为J1，将实验舱等效到肩关节处的集中转动惯量为J2，腕关节传动链等效到末端的刚度为k1，粘性阻尼为c1，肩关节传动链等效到末端的刚度为k2，粘性阻尼为c2，广义坐标θ1和θ2分别为腕关节和肩关节相对于运动停止前平衡位置的角位移，其为时间t的函数。 转位机构制动过程动力学模型如图3 所示。

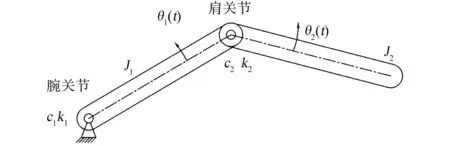
图3 转位机构制动动力学模型Fig.3 Braking dynamics model of transfer mechanism

根据达朗贝尔原理，对转位机构制动过程建立动力学方程为公式（1）所示。

式中：［J］为惯量矩阵，［C］为阻尼矩阵，［K］为刚度矩阵，｛θ¨｝为关节的角加速度矩阵，｛θ·｝为关节的角速度矩阵，｛θ｝为关节的角位移矩阵，｛M｝为激励力矩矩阵。

由于转位过程实验舱姿控发动机关闭，不会对实验舱产生激励力矩，因此｛M｝＝0，带入系统参量则动力学方程（1）改写为式（2）。

3 数值计算分析

3.1 理想状态的时域动态响应

不考虑关节传动链摩擦和间隙的理想状态下，动力学方程（2）为二阶常系数线性微分方程组，可以求得方程的解析解［9］。 由于转位动力学模型为两自由度系统，因此在自由振动时存在ω1和ω2两个固有频率。 当系统按照频率ω1振动时，J1和J2的振幅比记为r1；当按照频率ω2振动时，J1和J2的振幅比记为r2，则振型矩阵如式（3）所示。

由于转位机构肩关节和腕关节采用模块化设计，两者参数相同，有k1＝k2，c1＝c2。 令系数如式（4）所示。

则方程（1）中的矩阵［C］、［J］和［K］满足式（5）的比例阻尼要求。

式中：α和β为比例常数。

将式（5）带入方程（1）得式（6）。

由于振型矩阵对惯量、刚度和阻尼矩阵具有正交性［10］，因此通过坐标变换的方式可将方程（6）解耦，使其解耦的主坐标记为｛q｝。

定义线性坐标变换，如式（7）所示。

式（7）两边分别对时间求一次导数和二次导数，得式（8）、式（9）。

式中：J′1和J′2为主惯量，C′1和C′2为主阻尼，K′1和K′2为主刚度。

方程（11）已将坐标变换后的两关节角位移解耦，为两个独立方程，其中的q1和q2可通过单自由度阻尼振动微分方程求得解析解［11］，如式（12）所示。

式中：ζ为阻尼比，ωn为圆频率，q0＝q（t＝0），＝q·（t＝0）。

｛q｝解析解求得后，可通过式（7）求得｛θ｝的解析解。

根据工程实践结果，选取如下转位过程中的惯性参数和关节参数进行分析：J1＝100 kgm2，J2＝1×106kgm2，c1＝c2＝2×105Nms／rad，k1＝k2＝2×104Nm／rad，ω＝0.006 rad／s。

转位过程中存在腕关节转动和肩关节转动2 种情况。 腕关节转动时，J1以角速度ω绕腕关节转动，同时带动J2也以ω的角速度绕腕关节转动；肩关节转动时，腕关节保持不动，仅J2以角速度ω绕肩关节转动。

因此，得到腕关节转动停止后的动力学方程初始条件为：θ1（0）＝0，（0）＝0.006 rad／s，θ2（0）＝0，（0）＝0.006 rad／s。 肩关节转动停止后的动力学方程的初始条件为：θ1（0）＝0，

通过｛θ｝的解析解，可得到腕关节和肩关节角位移随时间变化的动态响应曲线。 图4为腕关节转动停止后的两关节角位移动态响应曲线，图5 为肩关节转动停止后的两关节角位移动态响应曲线。 从曲线可以看出，腕关节和肩关节转动停止后关节动态响应表现为欠阻尼振动形式。

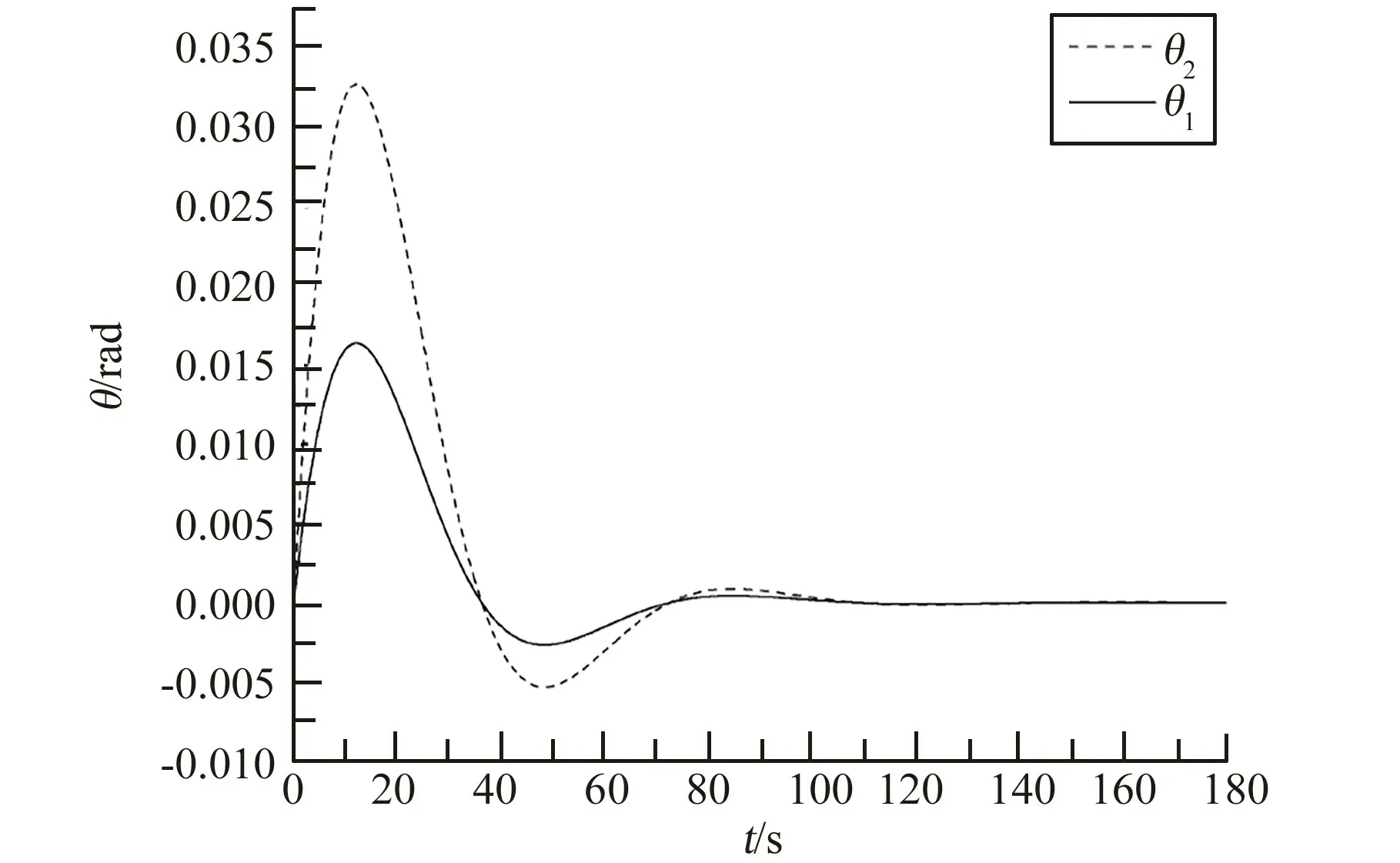
图4 理想状态下腕关节转动停止后的关节动态响应曲线Fig.4 Dynamic response curve of wrist joint after rotational stop under ideal condition

图5 理想状态下肩关节转动停止后的关节动态响应曲线Fig.5 Dynamic response curve of shoulder joint after rotational stop under ideal condition

同时可以看出腕关节转动停止后和肩关节转动停止后的角位移响应几乎一致。 这是由于平面运动刚体的动能［12］如式（13）所示。

式中：Jp为刚体对于瞬时轴的转动惯量。

由于J1大小仅为J2的万分之一，制动时需要缓冲的动能主要来自于J2，因此腕关节是否存在初始角速度对制动后的角位移响应影响可忽略。

肩关节转动停止后θ1最大振幅为0.0164 rad，θ2最大振幅为0.0328 rad，两者角位移在141 s 后衰减至零。 由于肩关节和腕关节在动力学系统中为串联形式，因此肩关节角位移θ2等于腕关节角位移θ1叠加上J2相对于J1的角位移变化量。

3.2 考虑摩擦和间隙的时域动态响应

3.2.1 仅考虑摩擦的时域动态响应

转位过程中实际产品的传动链是存在摩擦的。 考虑将传动链中的摩擦等效为关节末端的摩擦阻尼T， 其方向总与关节运动方向相反，大小为－Mfsgn（θ·），Mf为摩擦力矩，sgn 为符号函数。腕关节和肩关节处的摩擦阻尼矩阵记为｛T｝。 此状态下粘性阻尼和摩擦阻尼同时起作用，动力学方程如式（14）所示。

式（14）为非线性微分方程，采用龙格－库塔方法［13］对系统动态响应进行数值计算。 根据同类产品研制经验，取摩擦力矩Mf＝20 Nm 来进行分析。

以肩关节转动停止后为例进行分析，得到腕关节和肩关节角位移随时间变化的动态响应曲线，如图6 所示。 由图可知，考虑摩擦阻尼后腕关节角位移θ1最大振幅为0.0153 rad，肩关节角位移θ2最大振幅为0.0315 rad，两关节角位移在112 s 后衰减至零。 通过与理想状态下的制动过程对比，考虑摩擦阻尼后对最大振幅影响较小，θ1与θ2最大振幅分别减小了7%和4%。 考虑摩擦阻尼后对稳定时间影响较大，时间缩短了21%。由上分析可知，真实产品传动链由于存在摩擦阻尼，其制动过程中稳定时间将比理想状态下计算结果缩短。

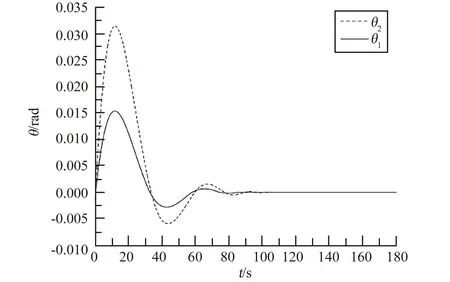
图6 考虑摩擦阻尼情况下肩关节转动停止后的关节动态响应曲线Fig.6 Dynamic response curve of shoulder joint after rotational stop under friction damping

3.2.2 同时考虑摩擦和间隙的时域动态响应

由于转位机构关节采用齿轮传动，因此关节传动链必然存在齿轮空程。 将空程折算至关节传动链末端为间隙2b，则腕关节和肩关节等效到传动链末端的刚度k、粘性阻尼c和摩擦阻尼T为角位移θ的函数，三者整体呈现为非线性。 当角位移θ处于空程中时，k、c、T大小为零，当θ处于非空 程 段 时 呈 现 出 原 有 特 性， 如 式（15） ～（17）所示。

选取摩擦力矩Mf＝20 Nm，间隙b＝0.01 rad，通过数值计算方法来进行角位移动态响应分析。以肩关节转动停止后为例进行分析，动态响应曲线如图7 所示。 通过曲线可知，θ1最大振幅为0.027 rad，θ2最大振幅为0.053 rad，振幅相比无空程的情况变大是因为叠加了间隙量b。 稳定后腕关节角位移θ1为－0.01 rad，稳定后肩关节角位移θ2为－0.02 rad，说明腕关节和肩关节角位移最终稳定在间隙内，即关节在制动结束后的定位精度不大于间隙量b。θ1和θ2的稳定时间为178 s，间隙的存在使关节角位移稳定时间增大59%，原因是关节运动在间隙中时无阻尼力矩和摩擦力矩的作用，动能无衰减。

图7 考虑摩擦阻尼和0.01 rad 间隙情况下肩关节转动停止后的关节动态响应曲线Fig.7 Dynamic response curve of shoulder joint after rotational stop under friction damping and 0.01 rad gap

选取摩擦力矩Mf＝20 Nm，间隙b＝0.015 rad，通过数值计算方法来进行角位移动态响应分析。以肩关节转动停止后为例进行分析，动态响应曲线如图8 所示。 通过曲线可知，θ1最大振幅为0.032 rad，θ2最大振幅为0.063 rad，振幅因间隙量的增大而变大。 稳定后腕关节角位移θ1为－0.015 rad，稳定后肩关节角位移θ2为－0.03 rad，说明腕关节和肩关节角位移最终也是稳定在间隙内。θ1和θ2的稳定时间为207 s，间隙的增大使关节角位移稳定时间继续增大16%，这是因为关节角位移在增大的间隙中的无阻尼运动时间延长导致。

图8 考虑摩擦阻尼和0.015 rad 间隙情况下肩关节转动停止后的关节动态响应曲线Fig.8 Dynamic response curve of shoulder joint after rotational stop under friction damping and 0.015 rad gap

考虑传动链摩擦和间隙后，关节角位移动态响应曲线与理想状态差异较大。 因此在转位过程分析时，应该考虑摩擦和间隙对制动过程的影响，从而建立更为真实的动力学模型，以获得更为合理、准确的分析结果。

4 试验结果

对转位机构样机产品进行实测，得到稳态下摩擦力矩为18 Nm，关节末端间隙为0.012 rad。 在转位机构关节特性测试系统上进行制动动力学测试，如图9 所示。 试验工况为腕关节保持静止，肩关节按照0.006 rad／s 角速度匀速转动后断电制动，肩关节停止时刻为T0，测试结果及与计算结果的对比如图10 所示。 计算值与试验值的趋势一致性好，振幅的计算值与试验值最大误差为7%，定位精度的计算值与试验值的最大误差为8%，证明了本文所建立的动力学模型的合理性。

图9 转位机构制动动力学试验Fig.9 Braking dynamic test of transfer mechanism

图10 转位机构制动动力学试验值与计算值对比Fig.10 Comparison between experimental and calculated values of braking dynamics of transfer mechanism

5 结论

1）不考虑传动链摩擦阻尼和间隙的理想状态的转位制动过程中，腕关节和肩关节转动停止后角位移动态响应为欠阻尼振动形式，随着时间变化逐渐衰减至零。

2）由于实验舱的转动惯量远大于转臂转动惯量，腕关节转动停止和肩关节转动停止后的角位移响应几乎一致，在进行转位参数设计时可以只以肩关节转动停止后的情况开展。

3）在考虑传动链摩擦阻尼后的转位制动过程中，摩擦阻尼对角位移响应的最大振幅影响较小，但对转位到位后的稳定时间影响较大，稳定时间大幅降低。

4）在考虑传动链间隙的制动过程中，刚度、粘性阻尼和摩擦力矩整体呈现为非线性，腕关节和肩关节角位移响应具有非线性特性。

5）转位到位后的关节定位精度取决于关节的间隙量，间隙量应作为设计的重要控制量。

6）关节间隙的存在使得关节的稳定时间大幅延长，转位机构的设计不能忽略间隙的影响。