基于非线性相对运动方程的碰撞规避机动规划方法

李佩钰， 杨 震∗， 罗亚中

（1.国防科技大学空天科学学院， 长沙 410073； 2.空天任务智能规划与仿真湖南省重点实验室， 长沙 410073）

1 引言

随着航天技术的飞速发展，在轨空间目标的数量不断增加，太空资产面临的碰撞风险显著提高。 截止2023 年6 月，人类成功送入轨道的航天器超过15 797 颗，其中约有8218 颗仍然在轨活动［1］。 且在地球轨道上存在约有50 万颗1 ～10 cm 大小的碎片，1 mm 或更小的碎片估计超过1 亿颗［2］。 此外，星链（Starlink）等大型商业星座的部署［3］，进一步加剧了轨道环境的拥挤程度，卫星碰撞的可能性大幅增长。 由于空间目标在太空高速飞行，微小的碰撞也会产生严重的后果，可能导致航天器失效甚至解体［2］。 太空资产是国家战略资产［4］，通过轨道机动规避碰撞风险是保护太空资产的重要手段。

碰撞规避的首要步骤一般是对目标进行接近分析，即通过定轨结果预报两目标的接近距离、接近时刻等参数。 现有航天器接近分析方法主要有解析法和数值法2 类。 解析法是基于轨道根数之间几何关系设计解析表达式，通过求封闭函数的解，获取接近事件的信息。 Hoots 等［5］通过一系列筛选排除大量目标，而后考虑共面或异面情况，确定两目标之间距离小于设定阈值时的最接近点和接近区间。 目前解析法相关研究大多是基于Hoots 方法开展［6-7］。 由于解析法对轨道类型十分敏感，在摄动影响下存在漏报的问题。 而随着计算能力提升，数值法成为主要接近分析方法，即采用逼近、插值等近似计算方法，获得目标接近时刻状态信息。 基于部分已知轨道状态，Alfano等［8］采用数值计算方法，通过计算定义距离函数的三次多项式方程得到接近时刻，并推导了误差椭球区域进出点及进出时间，此方法即A-N（Alfano-Negron）算法。 李鉴等［9］针对A-N 算法中多项式易丢根情况，对其求根方法进行了改进。Denenberg 等［10］基于A-N 算法，对结果精度和速度进行折中计算，建立了更高效的接近分析方法。由于航天器可能存在与同一个目标在一定时间段内出现多次接近，或与多个空间目标同时存在接近的风险，因此为确保航天器的控后轨道跟任何已知目标在一定时间范围内都不能发生接近风险，需要研究考虑多目标多圈次场景下的适用于碰撞规避的接近分析方法。

基于接近分析得到接近距离和接近时刻等参数后，需定义并计算碰撞风险评估指标来衡量碰撞规避过程中目标间的碰撞风险。 碰撞风险评估指标的计算方法目前主要有Box 区域判定和计算碰撞概率2 种。 Box 区域判定方法对位置关系进行考虑，是航天飞机碰撞预警的主要手段［11］。 李甲龙等［12］对碰撞风险的评估适用标准进行分析，在预报精度较差时，可利用Box 区域判定对风险进行综合评定。 李翠兰等［13］考虑轨道预报及轨控时的偏差传播特性，提出了Box 动态阈值设定方法。 碰撞概率计算考虑了空间目标之间的相对几何关系以及位置速度的误差协方差，是目前使用较为广泛的风险评估方法。 Chan［14］针对航天器长期碰撞建模问题，考虑椭球协方差误差，利用3 个随机变量替代笛卡尔坐标系下的位置速度，计算碰撞概率。 Patera［15－16］利用三维对称协方差误差矩阵，解决非线性相对运动下的碰撞概率问题，且为准确得出概率增量，将相遇段分成片段，将增量求和得到总概率值。 计算碰撞概率的方法在工程上易受测量精度及动力学模型的影响，当轨道精度不足时，难以保证误差协方差的准确，使用起来并不方便。 对比之下采用Box 区域估计方法进行风险评估简单效率较高，是更可靠更保守的方法［17－18］。

当航天器通过风险评估识别到碰撞风险时，需采取相应规避措施，即碰撞规避策略。 Patera等［19］基于开普勒传播对空间目标状态进行预报，并采用梯度法确定机动方向，进一步用一维求根方法得到机动大小，能够将碰撞概率降低到预期。于大腾等［20］定义了潜在的碰撞威胁区，以弧长为优化目标建立最优规避模型。 基于航天器机动可达域，张赛等［21］定义了威胁评价指标，实现了最小燃料下的多脉冲威胁规避方法。 Bombardelli等［22－23］利用数值方法对施加的脉冲机动与B 平面的位移之间的相对关系进行优化，得到使得碰撞脱靶量最大或碰撞概率最小时的机动规避策略。 以上理论研究针对碰撞规避机动优化问题皆提出了相应的解决方法。 但为提高规避策略的高效且兼顾可靠性，需要从控后轨迹的建立方式和考虑控制工程约束的方向出发，对机动时间及机动量进行优化，获得燃料消耗相对较小的碰撞规避机动方案。 现有研究考虑工程任务需求和约束的较少，且大多关注单次接近情况，对多圈次接近考虑不多。 同时若采用数值的高精度轨道积分预报避撞后的控后轨道，将使得优化环节计算量大，生成避撞机动方案的效率低。

本文基于航天器和空间目标轨道状态数据，首先利用高精度非线性相对运动解析方程［24］，快速构建控后飞行轨迹；而后以步长推进，通过航天器与空间目标的长时间多次接近分析，有效识别分析时段的全部接近信息，同时进行碰撞风险评估；最后建立优化模型，以半长轴为控制量，实现脉冲机动下的最优碰撞规避控制量和变轨时间选择，从而提高碰撞规避策略的安全性。

2 问题描述

碰撞规避背景下的机动规划需要对目标之间的相互关系进行分析，识别与航天器碰撞风险较大的空间目标。 由于空间目标数量和分析时间不断增加，如何快速预报风险且提高工程上应用的适配性，一直以来是轨控安全性分析关注的问题。本文基于航天器精密星历及空间目标编目TLE（Two Line Elements）数据库，基于解析非线性相对运动方程快速构建控后轨迹，建立碰撞规避机动规划模型，流程图如图1 所示。

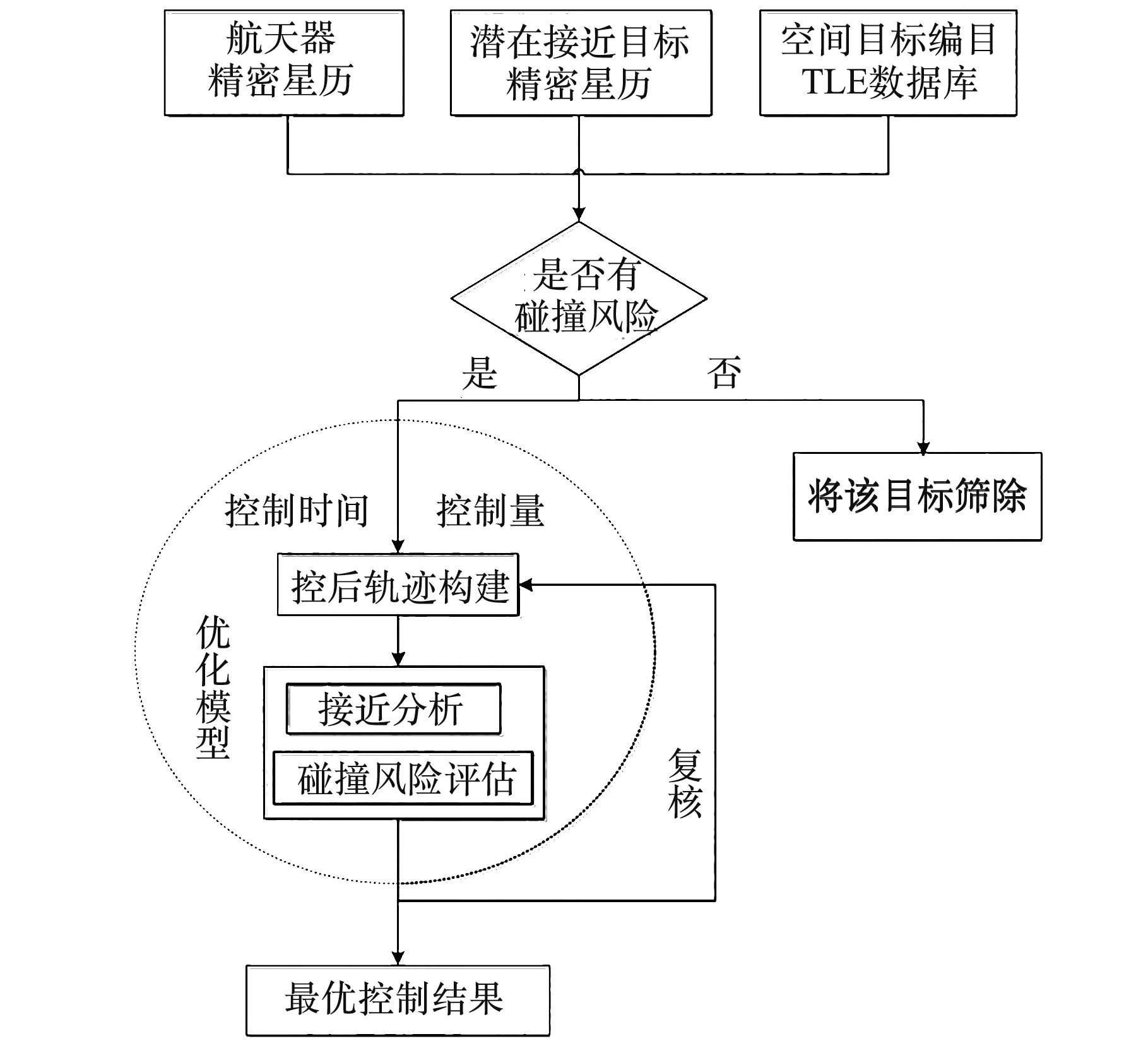
图1 碰撞规避机动规划方法流程Fig.1 Flowchart of collision avoidance maneuver planning method

首先，采用椭圆参考轨道，且包含J2 摄动项和中心引力梯度二阶项的解析非线性相对运动方程，快速构建控后轨迹。

其次，针对航天器与空间目标库大量数据，解决多圈次多目标下的接近分析问题。 将轨道信息粗筛选与多项式求根方法相结合，得到最接近距离对应的TCA（Time of Closest Approach）时刻、位置、速度等信息，同时进行基于等效距离量化指标的碰撞风险评估。

最后，由于航天器长期轨道维持一般只实施横向控制，抬高或降低轨道半长轴，因此可用半长轴为控制量。 在允许的控制时间和控制量区间内，优化规避机动时刻与机动量。

在不考虑控制偏差影响的情况下，再次调用接近分析模型，衡量控后轨迹的风险大小，获得该机动量下的所有接近分析目标的轨道信息，排除再次引入风险的可能性。

3 碰撞风险分析基础模型

3.1 坐标系定义与转移矩阵

定义地心惯性坐标系（Earth Central Inertial，ECI）如图2 所示。 其基准平面为天体平均赤道面，定义坐标原点O为地心，X轴位于平均赤道平面内并指向历平春分点，Z轴沿着垂直于赤道平面并指向北极，Y轴符合右手笛卡尔坐标系。

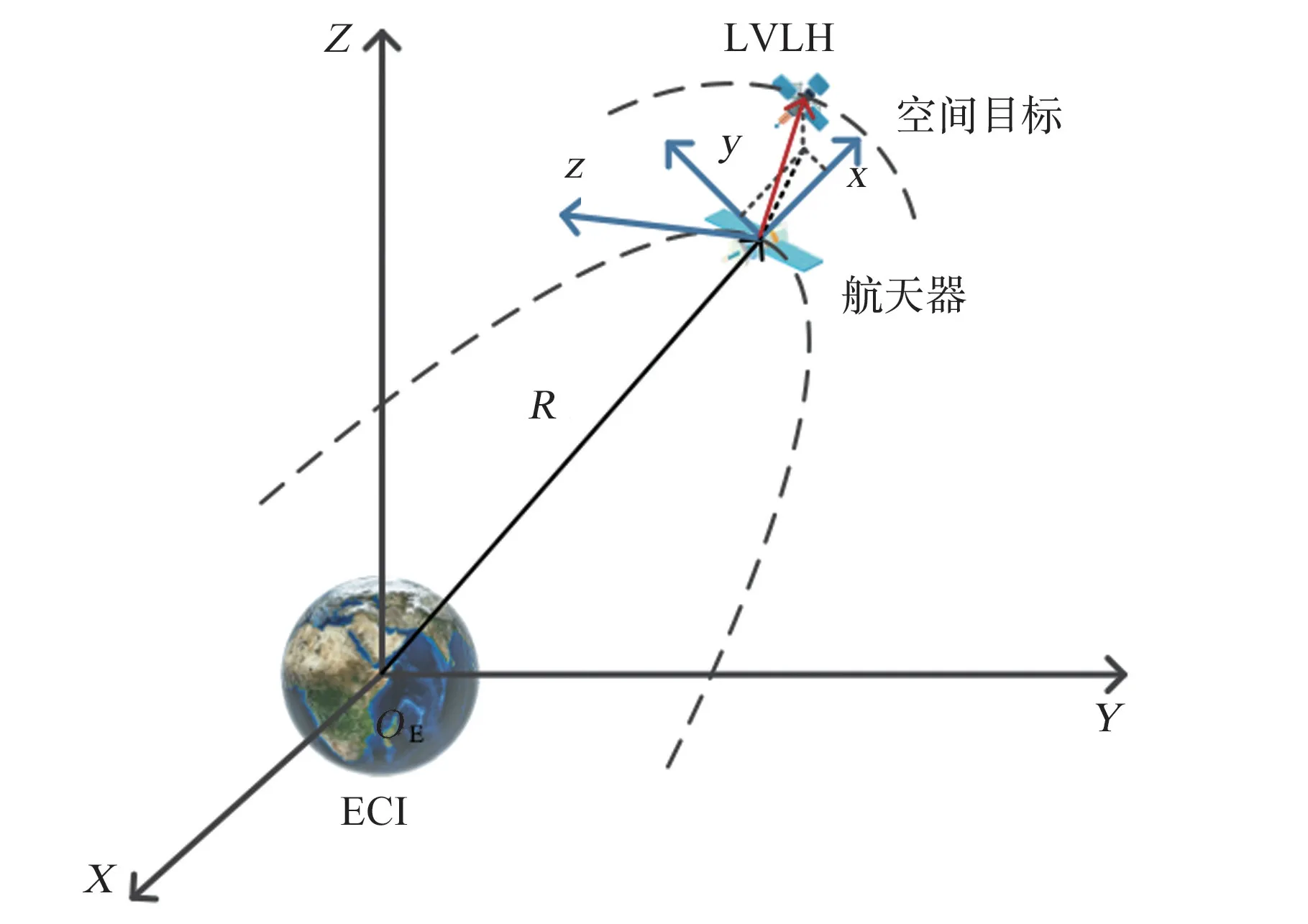
图2 航天器轨道坐标系Fig.2 Spacecraft orbital coordinate system

定义航天器当地轨道坐标系（Local Vertical，Local Horizontal， LVLH）如图2 所示。 其坐标原点为航天器，基准平面为航天器或空间目标的轨道平面，x轴沿着航天器位置矢量方向，z轴垂直于轨道平面，为正法线方向，y轴根据右手定则确定。

本文使用非线性相对运动方程时，航天器LVLH 坐标系与ECI 坐标系相互转换矩阵见式（1）［24］。

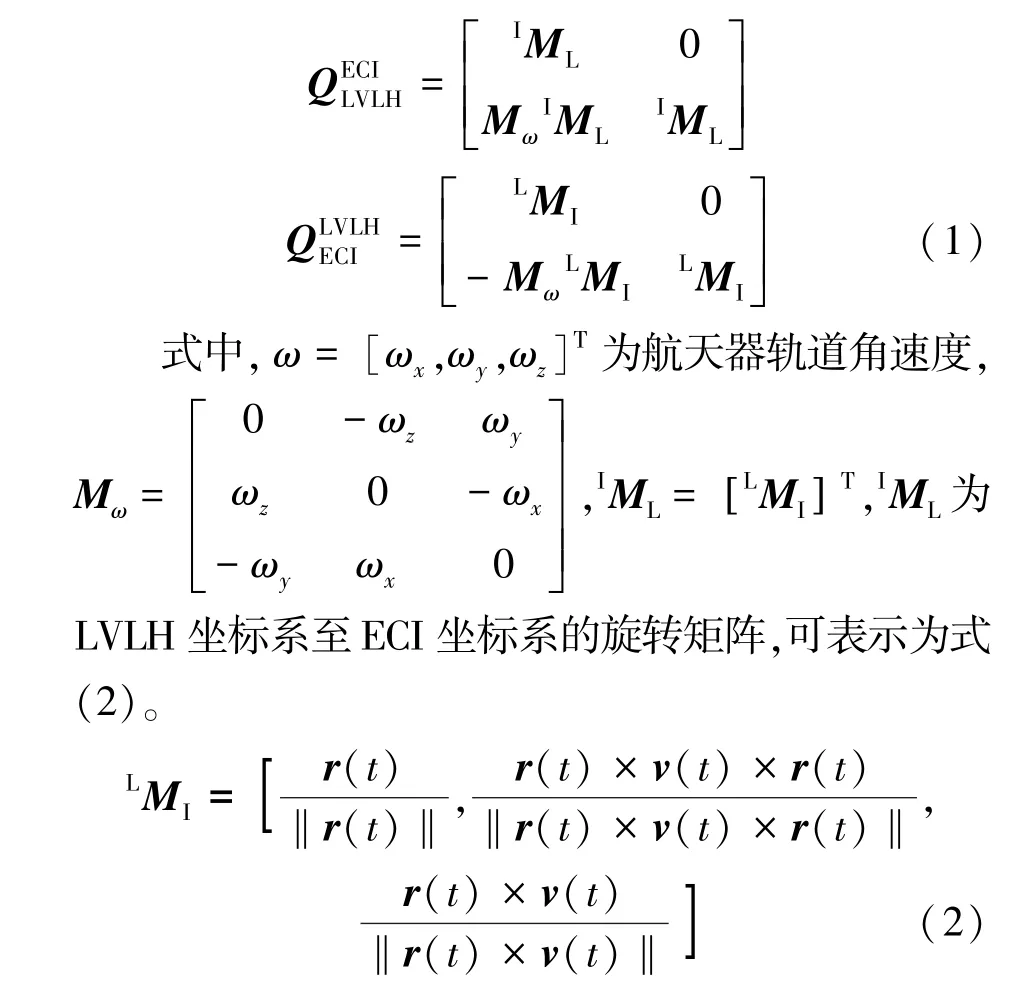
式中，r（t） 和v（t） 分别表示航天器位置矢量和速度矢量。

3.2 接近分析模型

由于空间目标库数据量较大，进行接近分析时需首先对目标进行筛选，本文分别利用轨道历元日期筛选、远近地点筛选和最大速度及加速度筛选，将大部分不可能接近的空间目标排除。 针对筛选后的目标，结合多项式方程求解所有目标的最接近时刻对应的距离和角度等轨道信息，即得到碰撞规避规划的风险量化参数。 接近分析的流程如图3 所示。

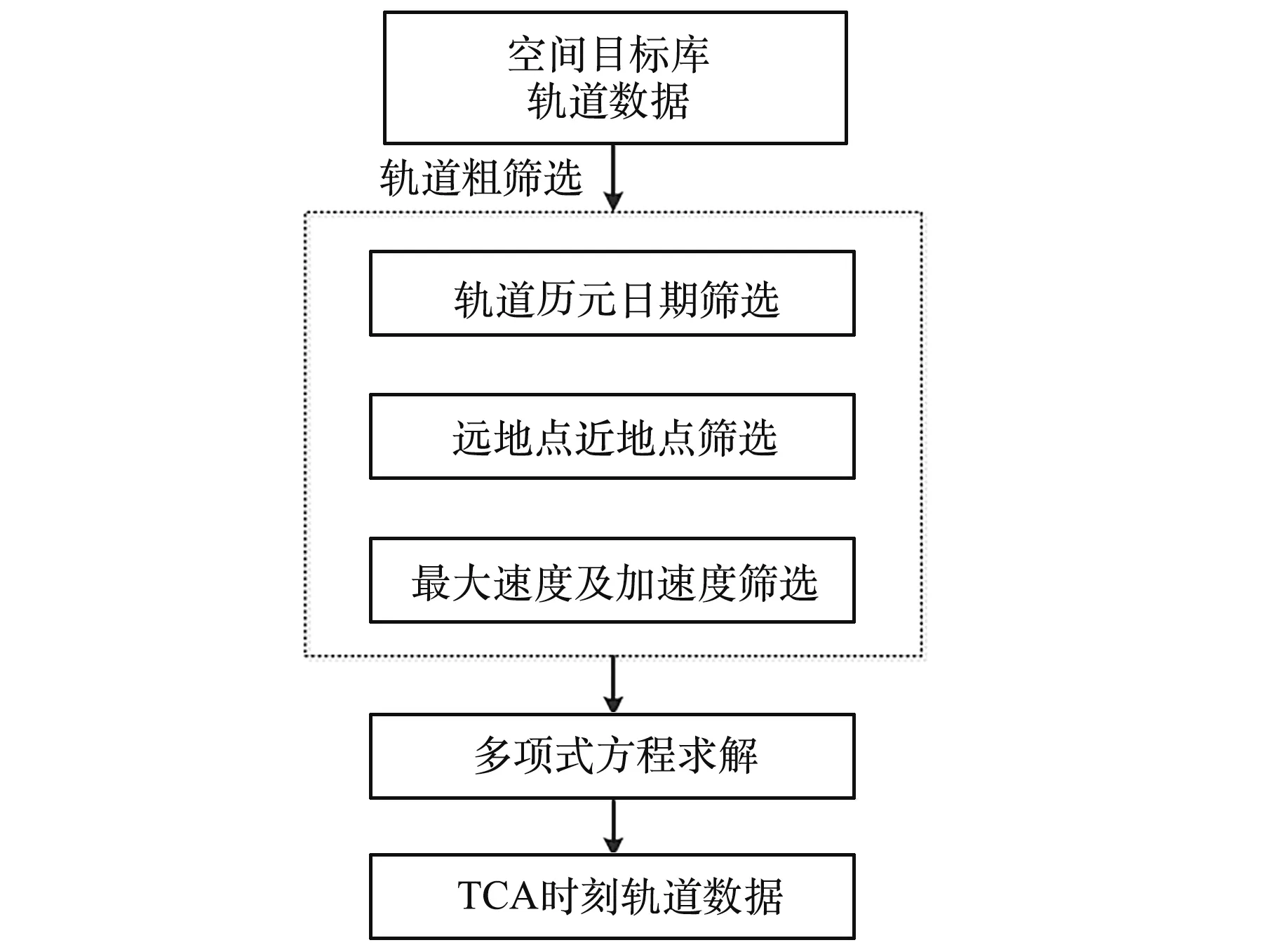
图3 接近分析过程Fig.3 Procedure of approach analysis

3.2.1 轨道接近事件筛选

已知碰撞分析的起始时刻t0和终止时刻tf，以及航天器精密星历，将该星历按时间步长Δt给出，时刻ti，i＝0，1，2，…，n－1 满足ti＋1＝ti＋Δt，tn＝tf，使用七阶拉格朗日插值法得到其位置和速度矢量Xch（ti） ＝[rch（ti），vch（ti）]T。 同时，根据空间目标编目数据库中每个空间目标的两行轨道根数TLE，采用SGP4 轨道预报模型，获得任意时刻空间目标的位置和速度矢量。

首先，筛选轨道历元日期。 提取空间目标TLE 数据中的历元时刻tTLE信息，设空间目标编目数据库中距离碰撞分析的起始时刻t0过长时（例如超过30 d），则不需要进行接近分析。 因此，轨道历元日期的筛选条件为式（3）。

而后，考虑目标之间的相对几何关系，分别计算分析开始时刻t0对应的航天器和空间目标的远地点及近地点高度，使用近地点－远地点筛选法，将不可能存在的碰撞点排除掉，筛选的标准［25］为式（4）。

式中，Q为远地点高度中的航天器和空间目标中的小者，q为近地点高度中的大者，D1为设定的近地点－远地点门限值。

对于通过筛选的空间目标，定义D2为危险距离，筛选掉大于该门限值的接近事件。 在碰撞分析的时间区间内，假设航天器在预报区间内以第二宇宙速度飞行时，依据步长分析航天器和空间目标之间的相对位置矢量rc＝［rc，x，rc，y，rc，z］T，设Rc，1为最大速度相对距离衡量指标［26］见式（5）。

式中，ve＝ 2μ／r。 若rc，x ＞Rc，1或rc，y ＞Rc，1或rc，z ＞Rc，1或rc＞Rc，1，那么在此时间区间内不可能发生接近事件。

最后，考虑地球引力加速度以及航天器和空间目标的相对速度，定义Rc，2为最大加速度相对距离衡量指标［26］见式（6）。

式中，D3为危险距离，若rc＞Rc，2，则通过安全距离筛选，该指标可进一步进行筛选。

3.2.2 接近时间识别

在ECI 坐标系中，根据航天器和空间目标的相对距离矢量为rc， 得到相对距离函数fc（t） 及其一二阶导数见式（7）［8］。

式中，rh和rs分别为航天器和空间目标位置矢量，rc＝rh－rs。

而后基于距离变化函数Pc（τ） 的三次多项式方程式（8），得到相对距离函数fc（t） 达到极小值点时的根τTCA，从而得到其对应的时间tTCA见式（8）［8］。

3.3 碰撞风险评估指标

根据接近分析结果以及轨道预报误差在横向较大，径向较小的理论基础。 基于工程经验建立的碰撞风险评估指标模型［17］。 将加权后的接近距离和径向距离中的最大值等效为航天器与空间目标之间的最近距离，作为碰撞风险评估的等效距离指标见式（9）。

式中，l＝1，2，…，N，j＝1，2，…，pl，N为在时间区间［tm，tf］内与航天器接近距离小于设定值dtol的空间目标数目，pl为第l个空间目标与航天器在时间区间［tm，tf］内的总接近次数，djl（tTCA）为航天器与第l个空间目标的第j个最接近距离，δxjl（tTCA） 为航天器与第l个空间目标在第j个最接近时刻相对位置矢量的径向分量。

等效距离指标sjl同时考虑最接近距离和径向距离，能安全高效进行航天器与空间目标间的风险评估。 当sjl越小时，碰撞风险越大，sjl越大时，碰撞风险越小。

同时，定义碰撞预警的黄色门限为Syellow、红色门限为Sred， 若sjl≤Syellow， 则为黄色警报，若则为红色警报。 对于红色警报的处置，一般需要通过执行轨道机动来规避碰撞风险，同时复核该避撞机动，保证不引起与所有编目空间目标新的碰撞风险。

4 避撞机动优化模型

4.1 控后轨迹快速生成

在碰撞规避的轨控策略规划中，由于空间目标数据库所包含的轨道信息量大，因此对于多圈次的碰撞安全分析，需要更高效的控后轨迹预报方式。 本文根据非线性相对运动方程，快速建立基于标称轨道的控后轨道。

自初始时刻，将标称状态Xi加上该时刻相对状态偏移量δxi，按照一定的步长高精度预报轨道，得到任意时刻的航天器相对运动状态Xi， 控后轨道构建示意图如图4 所示。

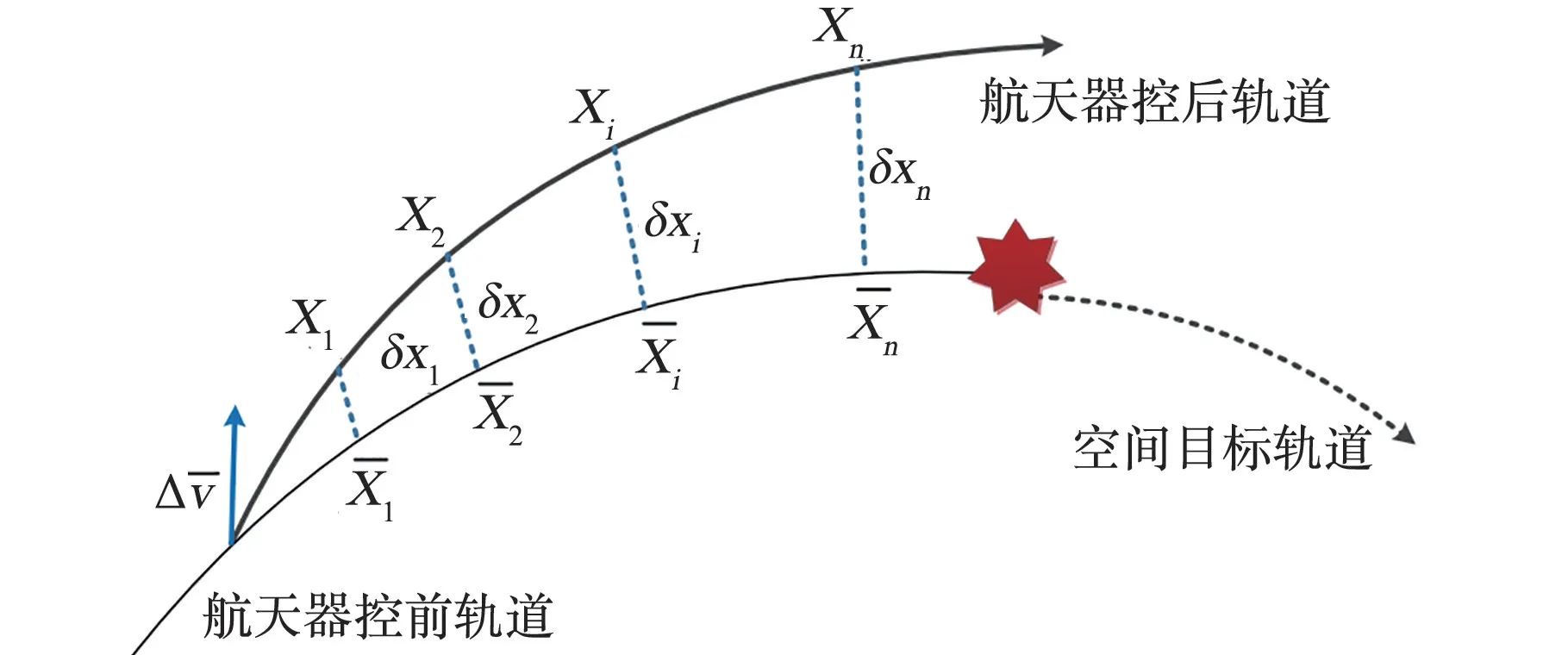
图4 轨控示意图Fig.4 Diagram of orbit control

已知需要执行碰撞规避的变量值为y＝［tm，Δam］，其中， Δam为半长轴控制量，根据高斯摄动方程，对应在航天器当地轨道坐标系下的横向脉冲机动控制量Δvt为式（10）。

定义tm时刻后任意t（t ＞tm）时刻航天器的控后轨道，相对于控前轨道的相对运动状态为式（11）。

以时间t为自变量，利用解析非线性相对运动方程，将δx(tm) 预报到tm时刻后的任意t时刻（t ＞tm），获得预报控后轨道的相对运动状态δx(t) ，见式（12）［24］。

式中，算子⊗表示张量积，即将2 个不同矢量空间中的矢量相乘得到一个更高维空间中的矢量。 状态转移矩阵Φ(t，tm) 与状态转移张量Ψ(t，tm) ，由航天器预报时间△t＝t－tm和基于精密星历的非奇异修正初始轨道的轨道根数em＝［a，w＋f，i，ecosw，esinw］ 计算，e为偏心率。P～－1（tm，tm）＝D－1（tm）P－1（tm），D（t） 为线性变换矩阵，P(t)为6× 6 的雅克比矩阵，Q(t) 为6×6× 6 的Hessian 矩阵。

最后，基于以上非线性映射，以及航天器控前轨道精密星历信息，得到控后轨道的任意时刻相对状态X～ch（ti），如式（13） 所示。

4.2 避撞机动优化建模

碰撞规避机动优化变量一般包括机动大小、机动时间、机动方向等。 本文基于航天器控前精密星历数据，通过七阶拉格朗日插值法得到的航天器位置矢量rch（t） 和速度矢量vch（t）。

对于控制约束，考虑测控跟踪计划，根据最早可控制时刻tlow和最迟控制时刻tup， 确定规避机动控制时间窗口。 同时，基于航天器平台机动能力限制和轨道维持约束，确定控制量门限，设定半长轴控制量上下限分别为Δaup和Δalow。

设碰撞规避机动执行时刻为tm，半长轴控制量为Δam，碰撞规避机动后的控后飞行轨迹与空间目标间的最近距离门限值Stol。 碰撞规避优化的设计变量为式（14）。

采用序列二次规划算法求解优化问题，优化模型应用实施具体步骤如下：

1）根据工程需要和规避需求，基于第3.2 节接近分析得到的风险量参数，运用式（9）的指标结果，进行碰撞风险评估。

2）调用第4.2 节的序列二次规划算法优化轨控安全策略，优化迭代总速度，并应用式（12）及式（13）的非线性相对运动方程，解算控后轨道。 当时间区间［tm，tf］内的所有接近等效距离均大于给定的门限值Stol， 得到最优控制时刻tc和半长轴控制量Δac。

3）根据基于优化算法模型得到最优时刻tc和半长轴控制量Δac， 再次调用第4 节的控后轨道预报模型，当航天器的最小接近距离大于设定的碰撞预警门限值时满足该条件，即通过轨控安全性复核，是可行的规避控制策略。

5 算例分析

对前文所述方法和模型进行仿真校验，仿真分析时段为2022／08／02 23：00：00 至2022／08／08 12：00：00，在轨航天器（Satellite）与控前存在碰撞风险的目标航天器（Target）的飞行轨迹通过工业部门获得，空间目标库TLE 数据由国外公开网站获得，如表1 所示。

表1 航天器与空间目标仿真数据源Table 1 Simulation data source of spacecraft and space targets

5.1 自然接近分析

项目组研发的自主航天任务设计软件ATK（Aerospace Tool Kit）编写实现了论文方法，采用ATK 仿真分析航天器与空间目标间的接近情况，设定接近距离门限100 km，分别取Syellow＝200 m，Sred＝50 m，得到接近距离较小的前3 个接近事件如表2 所示。

表2 航天器与空间目标接近事件列表Table 2 List of spacecraft and space target approach events

由表2 可知，Target 与空间目标国际编号53 316 的等效距离都小于200 m，都存在碰撞风险。 其中，接近时刻t∗为8 月5 日17：25：54 的等效距离最近，此距离下的航天器（Satellite）与潜在接近航天器（Target）的接近过程，如图5 所示。

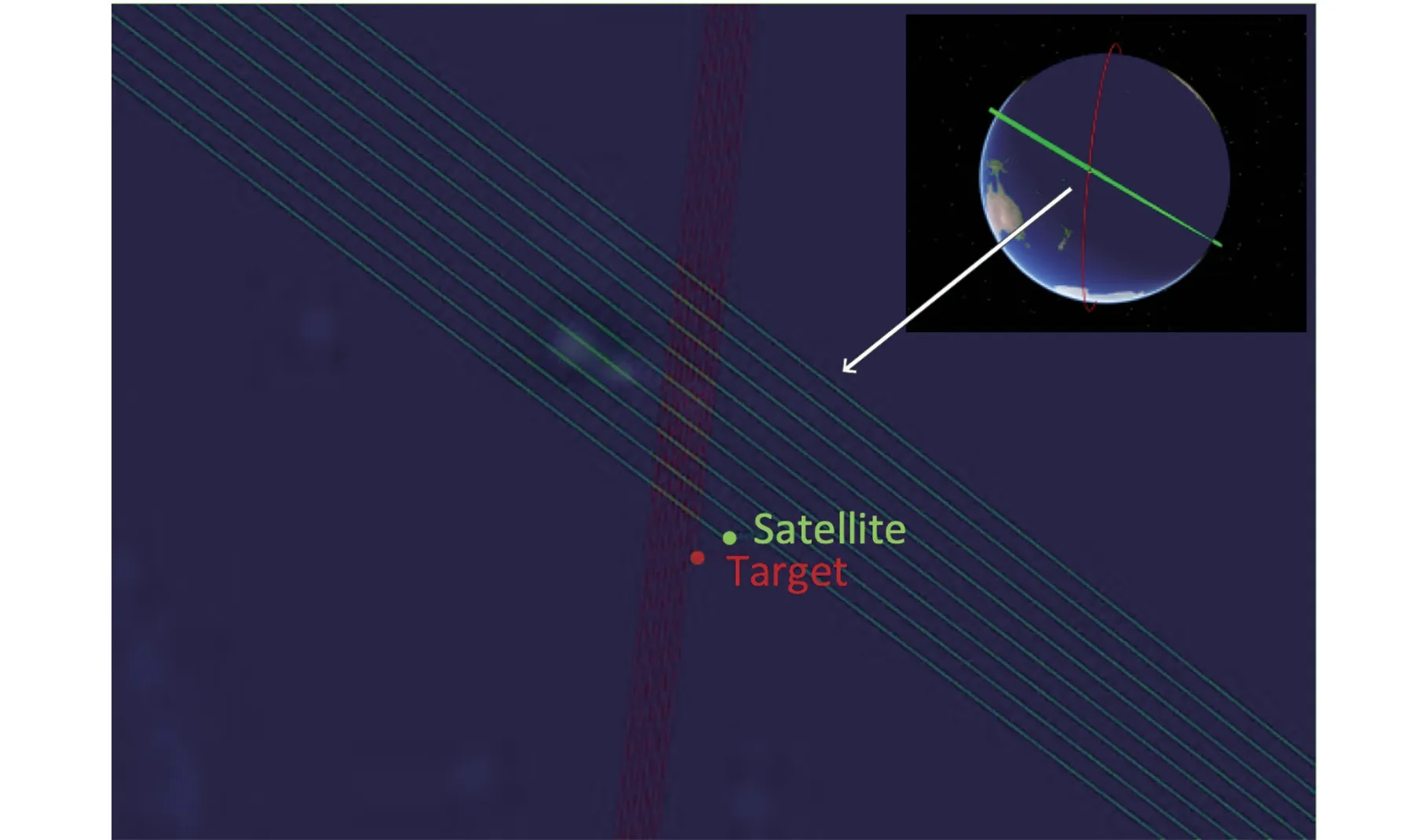
图5 ATK 仿真控前接近时刻Fig.5 ATK simulation of pre－control approach time

5.2 碰撞规避结果

根据航天器跟踪测控计划，确定规避机动控制时间窗口。 同时，由于Target 与空间目标国际编号53 316 同时存在碰撞风险，为规避所有目标的碰撞风险，时间区间的选择要早于碰撞风险时刻2022／08／03 20：28：34。

由此设置最早可控制时刻tm为8 月3 日15：37：14，最迟控制时刻tf为8 月3 日19：15：24，采用横向控制方式，抬高或降低轨道半长轴，控制量下限为Δalow＝－ 100 m，上限为Δaup＝ 100 m。调用序列二次优化算法，规划最优规避机动策略。

选取各机动策略tci和Δai，在原来自然交会接近时刻t∗的前后多个轨道周期内，分析规避机动控后轨道的多次接近最小等效距离，i＝1，2，3，…，得到如表3 所示的航天器与空间目标规避策略。 通过优化模型得到最优控制时刻和半长轴控制量，即第一个规避策略。 同时，依据等效距离排序，选取其他2 个满足s∗i≥200 m 且控制量较小的可行规避机动策略。

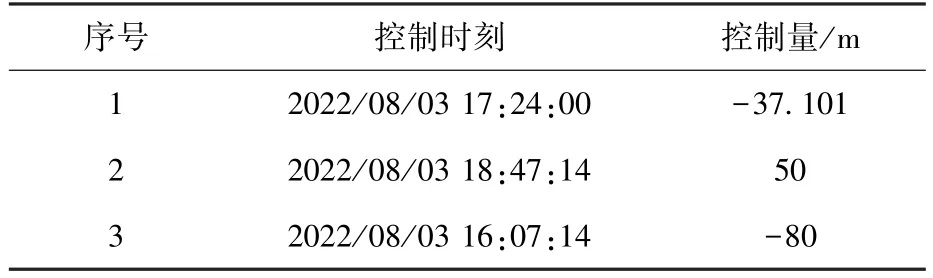
表3 航天器与空间目标规避策略Table 3 Avoidance strategy of spacecraft and space targets

5.3 机动复核结果

而后拟实施机动策略规避效果复核，分别选取3 个规避策略。 复核计算控制后在原来自然交会接近时刻t∗的前后多次接近条件，如表4所示。

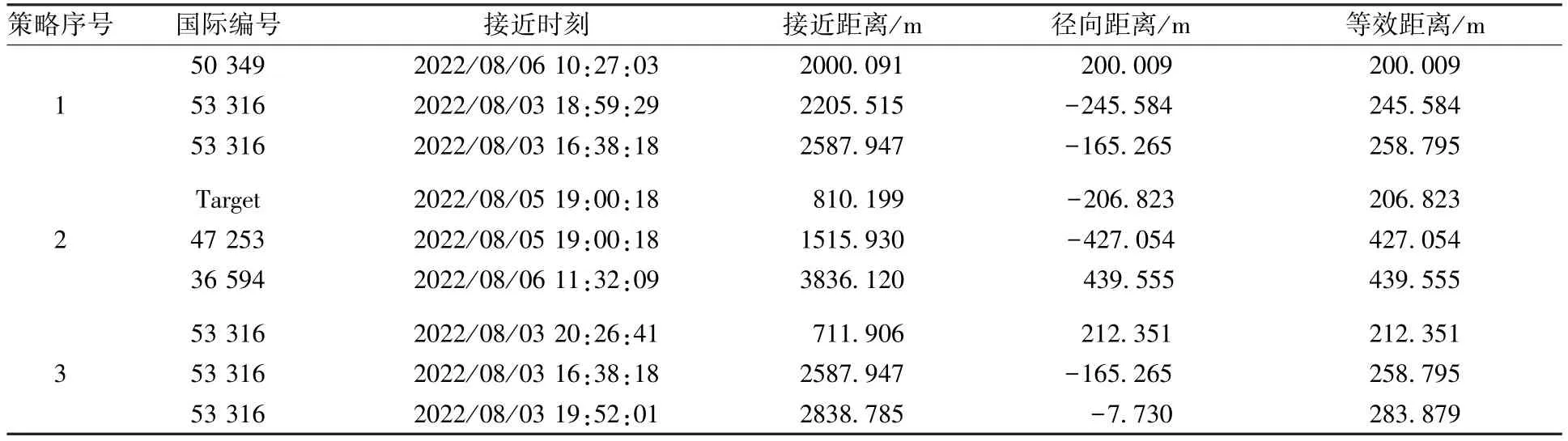
表4 3 个规避策略的控后规避效果Table 4 Control effects of three avoidance strategies

经过复核比对3 个可行的轨控策略的规避效果，得到最优控制时间和控制量给出策略，可在最小机动量下，规避所有目标。 最优控制时刻tc为2022 年8 月3 日17：25：09，最优半长轴控制量为Δa＝－37.114 m。 利用ATK 软件仿真航天器与空间目标的最优机动下的规避结果，如图6 所示。

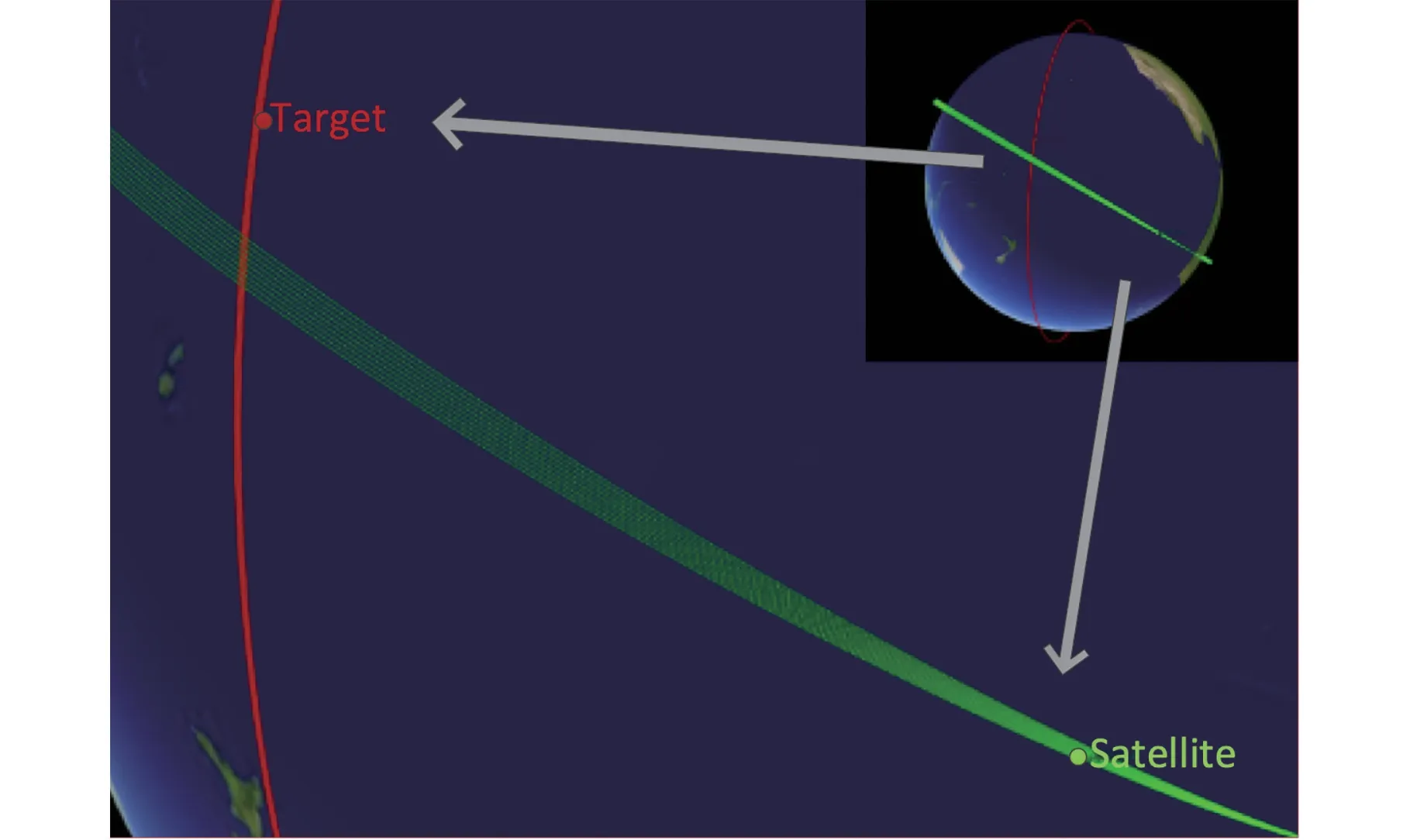
图6 ATK 仿真控后接近时刻Fig.6 ATK simulation of approach time after control

综上所述，本文提出的碰撞规避机动规划方法，对连续多个轨道周期出现多次接近的碰撞规避问题，能够避免控制后短期内再次出现碰撞风险的问题。

6 结论

本文针对空间目标碰撞风险持续上升，且境内可轨控测控时间区间限制严格的碰撞规避机动优化问题，提出了基于解析非线性方程的控后轨迹快速构建与碰撞规避机动优化方法。

1） 基于解析非线性相对运动方程快速构建控后轨迹，结合接近分析方法，提高了多目标碰撞风险分析效率；

2） 构建避撞机动优化模型，得到最优脉冲机动下的控制变量和时间，并建立了基于等效距离指标评估和复核碰撞规避效果的模型。

3） 仿真结果表明，所提方法能够准确识别在轨航天器的碰撞风险，可获得最优控制时间及半长轴控制量。