人工冻土复合幂-指数非线性强度模型

宋梓豪,姚兆明

(1.安徽理工大学 土木建筑学院,安徽 淮南 232001;2.矿山地下工程教育部工程研究中心,安徽 淮南 232001)

人工冻结法被广泛地应用于地铁隧道、深基坑等工程建设中,常用于提高土体的强度以及抗渗性。研究土体在冻结状态下的力学特性,可以为人工冻结法冻结壁的设计提供关键性指标,分析冻结土体在不同温度下的应力-应变行为是其中的核心问题。

岩土有着复杂的物理力学性质,很难通过一种本构模型来描述各种应力-应变曲线。孙谷雨等[1]基于温度和围压对冻结粉质黏土强度的影响规律,建立了以温度、围压为影响因素的冻结粉质黏土邓肯-张本构模型。张雅琴等[2]对冻土在不同围压、固结方式、应力路径条件下进行三轴剪切试验,在邓肯-张模型基础上建立考虑围压影响的冻结粉质黏土本构模型。但邓肯-张双曲线模型不能很好地反映土体三轴剪切过程中的应力-应变特性,尤其是冻土的软化特性。因此,近年来诸多学者在建立描述岩土应力-应变软化特性的本构模型方面做了大量的研究。张秀梅等[3]基于Weibull随机分布,在传统破坏模型的基础上建立了考虑空隙影响的统计损伤模型,能很好地反映岩石三轴压缩试验的软化特性。姚兆明等[4]基于Mohr-Coulomb屈服准则,运用Weibull随机分布和损伤力学理论建立了冻土统计损伤本构模型。王丽琴等[5]对结构性黄土进行三轴压缩试验,发现复合幂-指数非线性模型可以很好地描述不同软化型、硬化型的应力-应变曲线。汪恩良等[6]通过改进黏弹塑性模型,提出了与温度有关的描述超低温冻土应力-应变特性的复合方程。学者们为研究土体应力-应变特性还提出了指数模型[7]、复合指数模型[8]、复合指数-双曲线模型[9]、损伤模型[10-12]等本构模型。

在分析山东某矿区原状黏土单轴抗压试验应力-应变曲线规律基础上,建立了人工冻土单轴复合幂-指数非线性模型(CPE模型),通过拟合的方法求得模型参数最优解,得到了温度对模型参数的影响规律。所建立的人工冻土单轴CPE模型的参数少、易于确定且有明确的物理意义。模型计算结果表明,建立的人工冻土单轴CPE模型能够很好地反映冻结黏土单轴抗压应力-应变软化特性。

1 试验

根据山东某煤矿黏土(取土深度为200～340 m)土样参数确定人工冻土单轴CPE模型参数。确定每个试样高度为100 mm,直径为50 mm。在-10 ℃、-15 ℃、-20 ℃ 3个温度下进行单轴压缩试验,每个温度下进行3个平行试验,试验前需将试样在试验温度下冻结24 h。冻土单轴强度试验采用安徽理工大学自行研制的WDT-100型冻土试验机,该试验机最大竖向加载能力为10 t,精度为1%。试验荷载和试验数据均由计算机程序控制和采集。对所取试样进行了不同温度条件下的冻土单轴抗压强度试验,应力-应变关系曲线见图1。

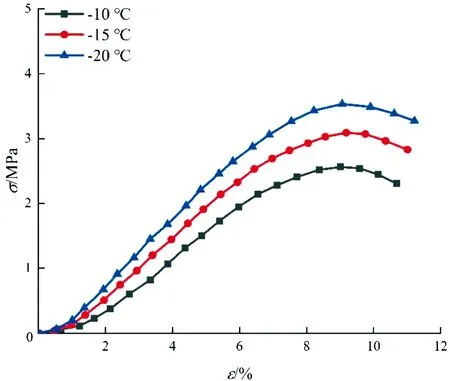
图1 应力-应变曲线

通过分析图1可以发现,冻结黏土的应力-应变关系有如下3个阶段:弹性阶段,随着轴向应力的增大,使得土体的密实度增加,土样的承载能力提高,此阶段的应力-应变曲线呈线性增长;塑性阶段,随着轴向应力的进一步增大,土体发生了不可逆的塑性变形,曲线呈非线性增长趋势,应力达到峰值,土体中冰颗粒与土颗粒的胶结物开始破坏,土体内部产生微裂缝,冻土内部损伤开始发展;屈服破坏阶段,应力达到峰值后持续加载,冻土的损伤导致承载能力降低,试验进入软化阶段,土体中的裂缝开始贯通并导致试样破坏。

图2为单轴抗压强度与温度的线性关系图。试验结果表明,冻土单轴抗压强度与温度具有很好的线性规律。随着冻土冻结温度降低,冻土单轴强度逐渐增大。这是因为随着温度降低,土体中水分逐步相变成冰,冻结土体中冰颗粒与土颗粒间胶结作用增强,冻土样的抗压强度也随之增大。

图2 单轴抗压强度与温度之间的关系

2 人工冻土单轴CPE模型

2.1 岩土体CPE模型

为了反映不同软化型、硬化型的应力-应变曲线,王丽琴等[5]对幂函数和指数函数进行理论分析,提出了一种非线性模型,其应力-应变表达式为

(1)

(2)

其中:b=0时,则应力-应变曲线CPE模型退化为幂函数模型;若令参数k=0,n=1,则其退化为指数模型;若令参数a=0,n=1,退化为另一种指数模型。可见,幂函数模型、指数模型均为本文CPE模型的特例。

2.2 模型参数求解及其物理意义

由于本次试验应力-应变曲线没有明显的残余强度阶段,故取k=0,并采用拟合的方式求取别的模型参数。图3～图6为人工冻土单轴CPE模型中不同参数对应的应力-应变曲线(以-10 ℃时的拟合结果为例)。

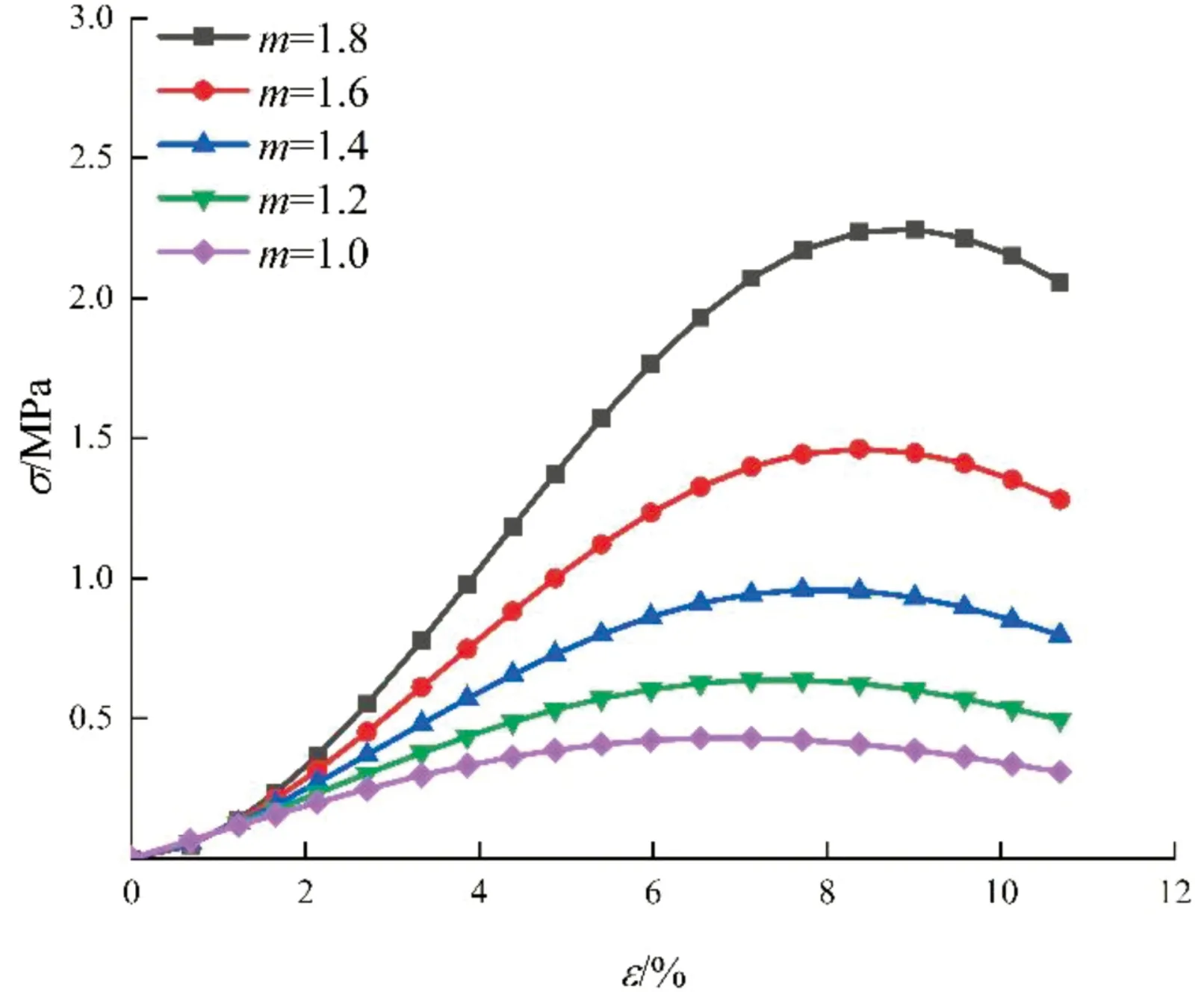
图3 不同参数m对应的应力-应变曲线

分析图3、图4可以发现,参数m与参数a均能反映峰值点之前的曲线状态,参数m能够描述峰值前应力-应变曲线的凹凸状态,m>1时,曲线呈下凹状,且随着m的增大,曲线的下凹程度越大,同时参数m越大,曲线达到峰值点时的变形越大。参数a对峰值前曲线状态的影响不明显,不同参数a的曲线达到峰值点时的变形一样。参数m与参数a均能对强度产生影响。

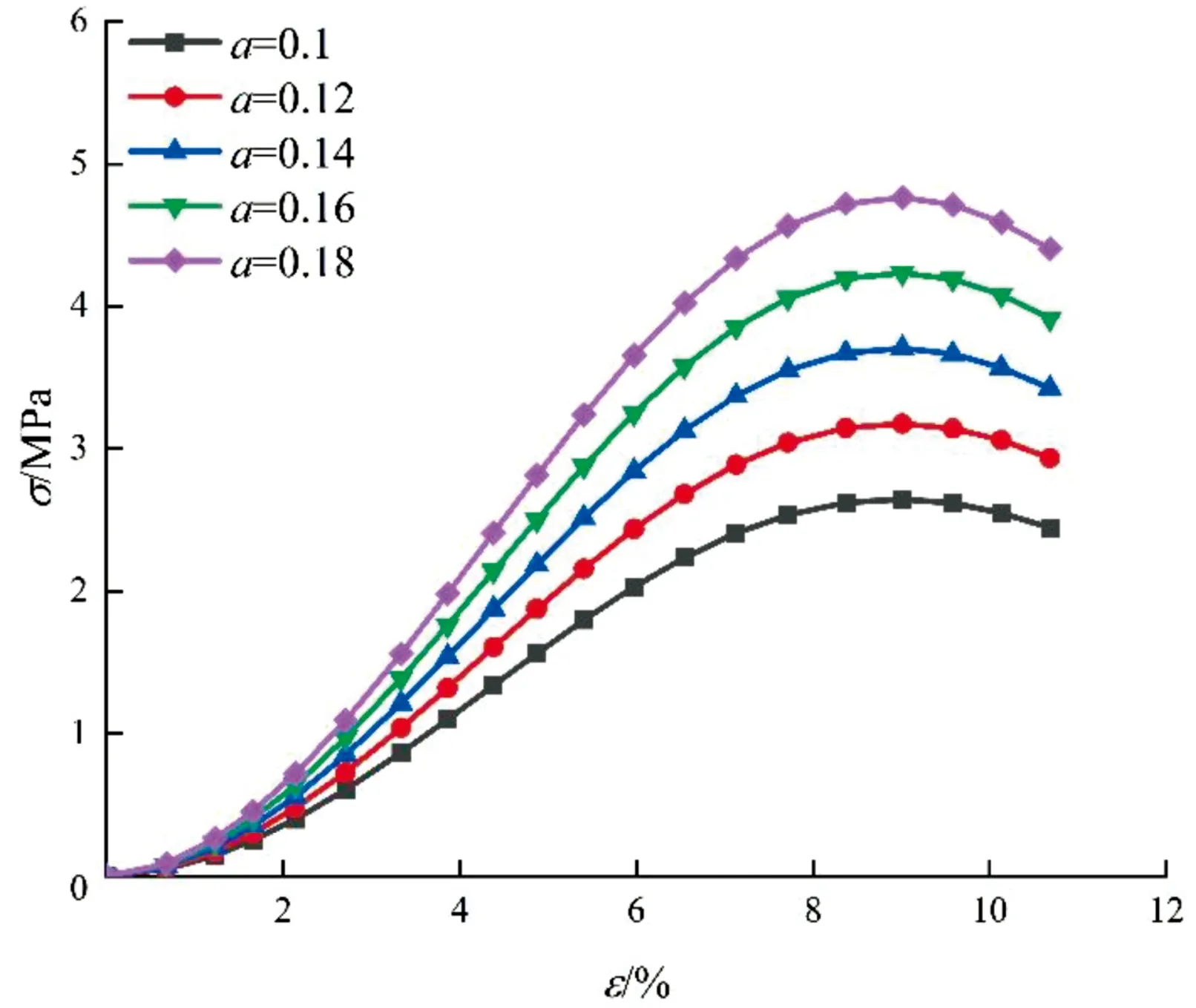
图4 不同参数a对应的应力-应变曲线

图5、图6反映了参数b与参数n对应力-应变曲线的影响。研究发现参数b与参数n应力-应变过程中的弹性阶段影响不明显,随着n值的增大与b值的减小,曲线屈服点逐渐后移,应力-应变曲线逐渐从软化型过渡到硬化型,二者能够反映冻土的强度与变形特性。

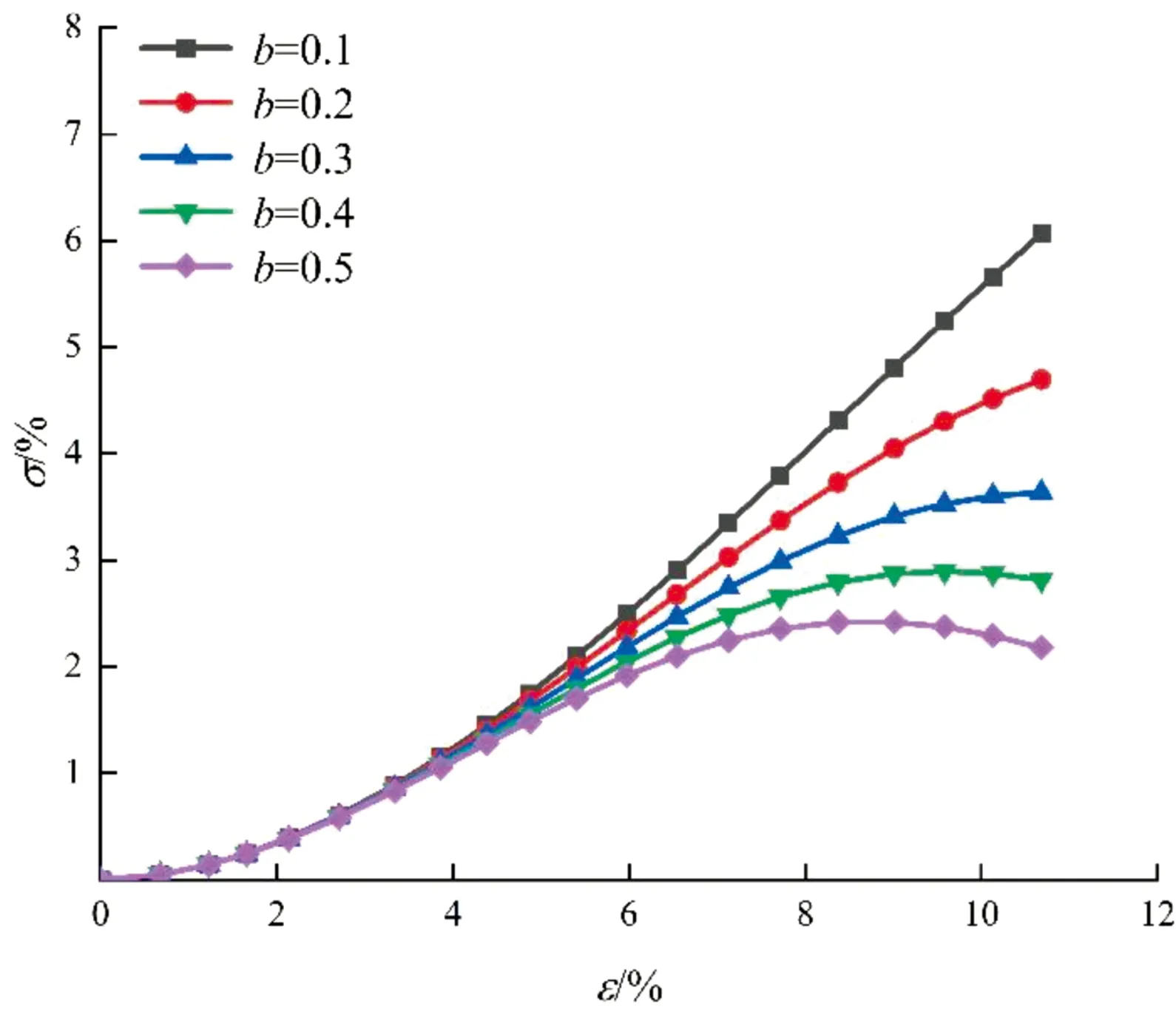
图5 不同参数b对应的应力-应变曲线

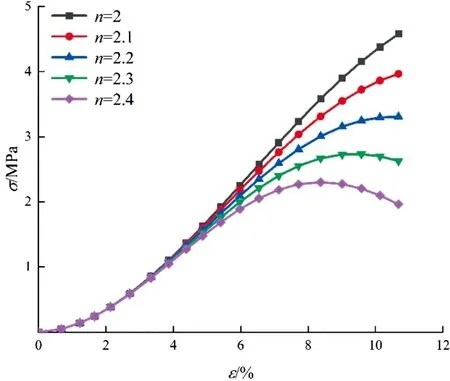
图6 不同参数n对应的应力-应变曲线

2.3 参数求解

(3)

对等式两边分别取对数

lnσ1=lna+mlnε1

(4)

式中:lna为拟合曲线的截距;m为拟合曲线的斜率。

不同温度下的拟合曲线见图7,不同温度下的参数a、m值见表1。

小柳河西岸有一旅馆，曰闹春楼，远离闹市却又得水陆交通之利。日本人占领蕲州后，城中许多旅馆店铺纷纷关门，原本清淡的闹春楼，生意却一天天地火红起来。

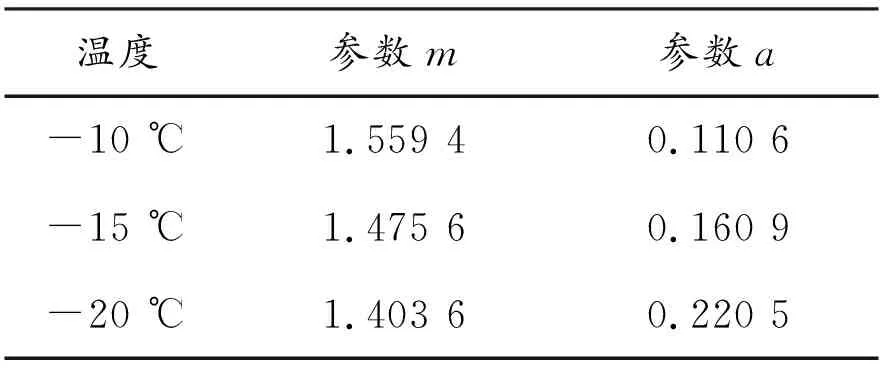
表1 不同温度下的参数m、a值

由表1可知,参数a、m均受冻结温度的影响,a随着温度的降低而增大,m随着温度的降低而降低。这是因为随着温度的降低,土体中含冰量增大,土体的塑性性能提高,土体达到同一应变时所承受的应力会进一步提高,进而使参数a增大。m可以反映土体压密阶段的变形特性,温度的降低增强了土颗粒间的胶结力,使得应力-应变曲线下凹程度降低。

(5)

对式(5)两边同时取对数

(6)

对等式两边分别取对数

lnq=lnb+nlnε1

(7)

当ε1→+∞时,式(2)中σ1→k。由于本次试验应力-应变曲线没有明显的残余强度阶段,假定ε1→+∞时,σ1→0,故取k=0。将表1中求得的m、a值代入式(2)中,再对试验数据进行拟合,求得参数b、n的最优解。不同温度的参数b、n值见表2。

2.4 模型拟合分析

研究发现,参数m、a均与温度呈线性相关,如图8、图9所示。

图9 参数a与温度T拟合

根据图8、图9可得参数m、参数a与温度之间的线性关系式为

m=1.712 3+0.015 6·T,R2=0.998 1

(8)

a=-0.000 9+0.011·T,R2=0.997 6

(9)

将式(8)、式(9)与不同温度下参数b、n代入式(2)中得到人工冻土复合幂指数非线性模型应力-应变方程

(10)

式中b、n值见表2。不同温度下的试验值与计算值对比如图10所示。通过对比发现计算值与试验值的变化趋势较为接近,人工冻土单轴CPE模型可以很好地描述冻土单轴压缩的应变软化曲线,并且参数易求,具有物理意义。

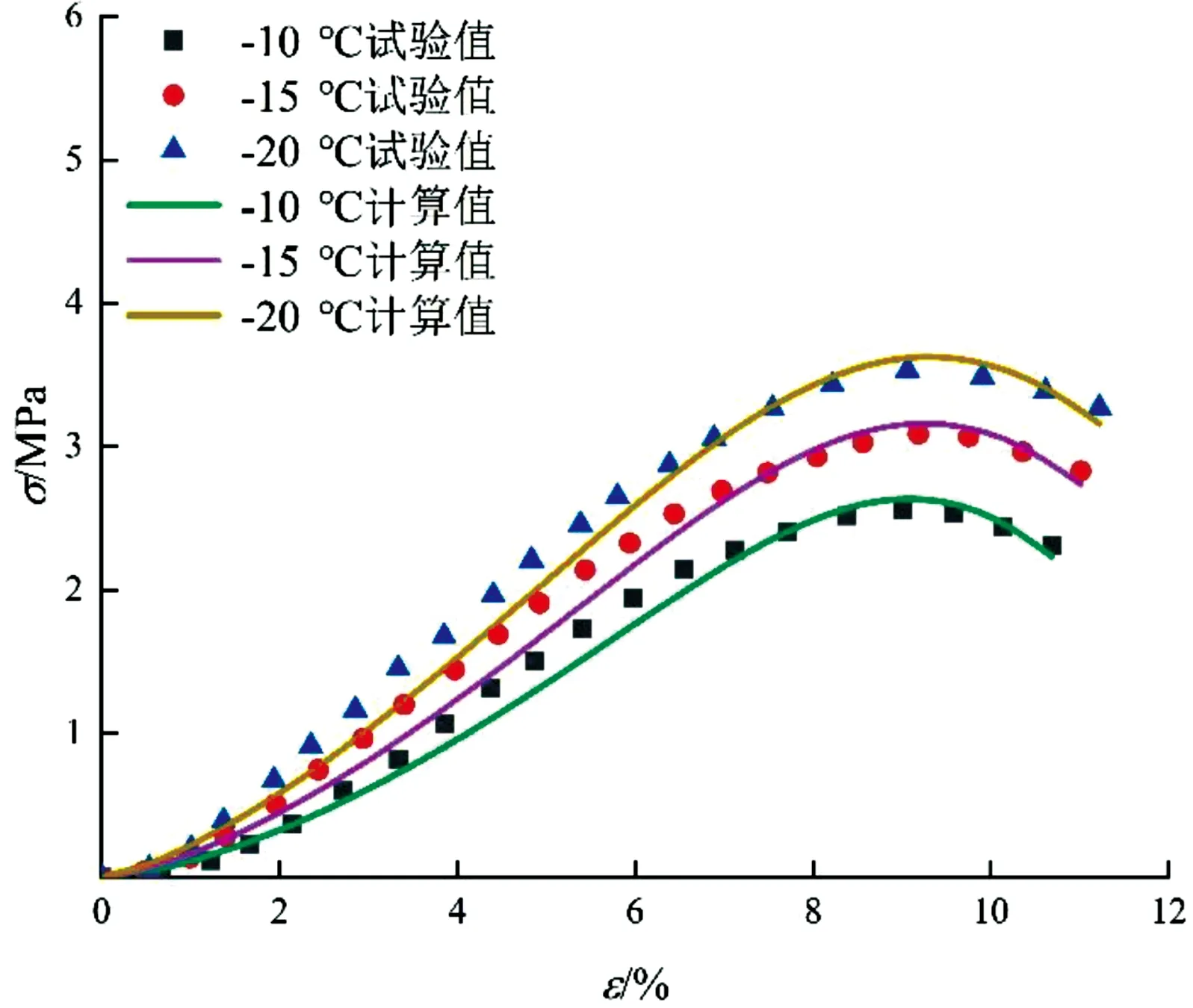
图10 试验值与计算值对比图

3 结论与展望

在分析岩土体CPE模型的基础上,引入温度函数,建立考虑冻结温度影响的人工冻土单轴CPE模型,并给出了参数求解方法,通过试验验证与分析,主要结论如下:

(1)冻结黏土的单轴抗压强度随着温度的降低而线性增加,考虑冻结温度影响的复合幂-指数非线性模型能很好地反映冻结温度对冻结黏土应力-应变发展特性的影响。

(2)模型参数易求解,物理意义明确,不同的模型参数影响着应力-应变曲线不同阶段的变化形态,模型参数均能反映冻土的强度与变形特性。

(3)人工冻土单轴CPE模型不能描述软化型曲线的局限性,且随着模型参数的改变,CPE模型能够反映不同状态的应力-应变曲线,适用性更强。

人工冻土压缩曲线有应变硬化和应变软化两种类型。所建的模型只验证了对软化型应力-应变曲线的实用性,下一步将在模型中进一步论证模型对硬化性曲线的适用性。为进一步拓展模型的适用范围,将在人工冻土三轴压缩试验基础上,分析所建模型参数与围压间的关系,建立能模拟人工冻土三轴压缩应力-应变的CPE模型。由于人工冻土具有结构性、各向异性,如何在模型中反映这两者对应力-应变的影响也将是下一步研究内容。