再生混凝土热传导细观数值模拟

王宇航,金立兵,吴 强,薛鹏飞,张业盛

(1.河南工业大学 土木工程学院,河南 郑州 450001;2.河南工大设计研究院,河南 郑州 450001)

建筑能耗在全国总能耗中的占比逐年上升,其中,建筑制冷、制热所需的能耗占建筑能耗的20%以上,有关研究预测这一数据将在2050年达到50%[1]。热导率是评估材料热传导性能的关键指标,再生混凝土具有较低的热导率,能有效减缓热量的耗散。SARGAM等[2]对掺入再生骨料的混凝土进行试验研究,发现其热导率有明显的降低。朱丽华等[3]通过正交试验研究了再生混凝土热导率的影响因素,结果表明再生粗骨料体积占比是影响再生混凝土热导率的主要因素,其次为再生细骨料取代率、水灰比以及单位体积用水量。ZHAO等[4]对高温环境下不同再生粗骨料取代率的再生混凝土进行试验研究,其热导率最大可降低47%。游帆等[5]对不同再生细骨料取代率的混凝土进行试验研究,结果表明,在全再生粗骨料的基础上,100%再生细骨料可显著降低再生混凝土的热导率,降幅可达23.6%。KAZMI等[6]研究表明,将经过预处理的骨料用于再生混凝土中可以有效提高其热导率。丁杨等[7]通过COMSOL有限元软件模拟了泡沫混凝土孔隙率与其热导率的变化关系,发现孔隙与热导率成负相关,孔隙会改变混凝土内部热量传输路径。张伟平等[8]借助二维混凝土细观模型,实现了稳态传热的数值模拟,分析表明粗骨料体积分数、骨料轴长比越大,混凝土热导率的变异性越显著。ZHU等[9]对混凝土的温度场进行细观数值模拟,结果表明“角效应”存在于多边形骨料的边缘处,使得多边形骨料混凝土温度场分布异于圆形或椭圆形骨料混凝土,同时,骨料掺量和骨料类型也会影响混凝土温度场以及热流分布。

学者大多在宏观层面对普通混凝土及再生混凝土热工性能开展了广泛的研究,鲜有从细观层面上揭示两者在传热性能方面的差异,以及再生混凝土内部各相组分对其传热性能的影响。本文借助MATLAB软件,建立包含天然粗骨料、新硬化砂浆、旧附着砂浆、新硬化砂浆与旧附着砂浆之间的新界面过渡层、旧附着砂浆与天然粗骨料之间的旧界面过渡层等五相组分的再生混凝土二维细观几何模型。采用COMSOL Multiphysics对所构建的模型进行热传导分析,通过研究再生粗骨料体积分数、五相热导率、界面过渡层厚度对再生混凝土热导率的影响,揭示再生混凝土热工性能的细观机理,为再生混凝土的推广应用提供理论依据。

1 再生混凝土细观模型的构建

现有的再生混凝土细观模型中,大多将混凝土粗骨料形状假设为理想化的圆形或椭圆形,与实际骨料形状差异较大。与天然粗骨料相比,再生粗骨料细观成分还包含旧附着砂浆、新界面过渡层、旧界面过渡层。因此,建立合适的再生混凝土细观模型也是传热分析的关键一环。图1为再生粗骨料细观层次示意图。

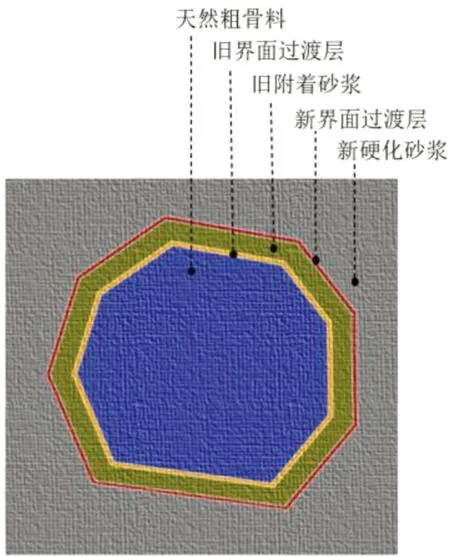
图1 再生粗骨料细观层次示意图

设置模型尺寸100 mm×100 mm,将再生粗骨料粒径划分为3个区间(5～10 mm、10～15 mm、15～20 mm)。基于连续级配理论,采用Walraven公式[10]可以计算出各粗骨料粒径区间的面积。研究表明,界面过渡层厚度在0～100 μm[11-12],并假设旧界面过渡层和新界面过渡层的厚度取值相同。

为了更准确地反映粗骨料空间属性的随机性,本研究采用Monte Carlo方法,通过MATLAB软件实现模型的构建。图2为MATLAB自编程序生成的不同再生粗骨料体积分数(20%、30%、40%、50%)的再生混凝土模型。

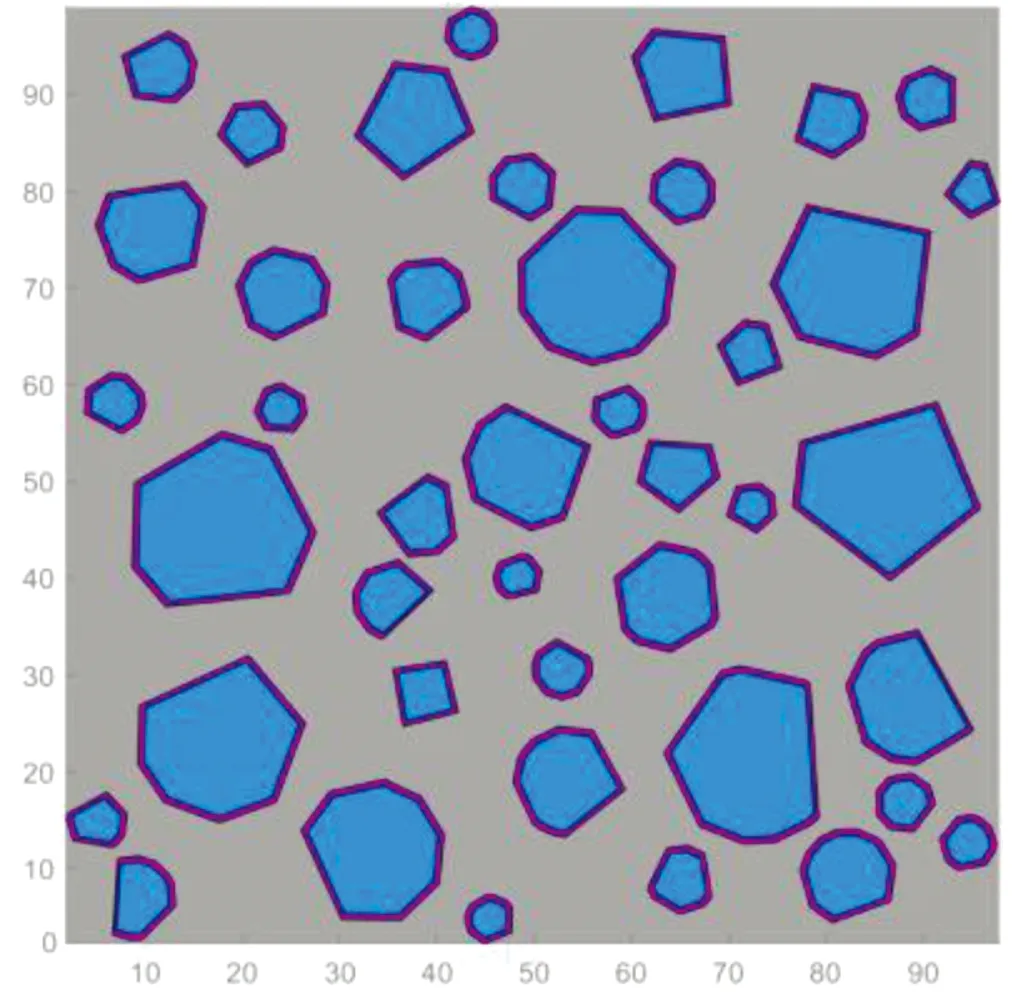
(b)再生粗骨料体积占比30%

(c)再生粗骨料体积占比40%

(d)再生粗骨料体积占比50%图2 再生混凝土二维模型

2 再生混凝土热传导数值模拟

2.1 理论基础

热传导是温度在混凝土内部的主要传输途径,温度梯度则是混凝土内部产生温差的前提[13]。热传导遵循傅里叶定律,公式为

(1)

当混凝土内部的热量不随时间而变化时,称为稳态热传导。稳态热传导同样也可以用傅里叶定律的微分形式来表示,公式为

(2)

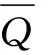
由于系统处于平衡状态,式(2)的左项整体为零。相应地,利用弹性力学的虚功方程和能量守恒方程,可以得到有限元单元方程组

[K]e{T}e={Q}e

(3)

式中:[K]e为单元温度矩阵;{T}e为单元节点温度向量;{Q}e为单元热流矩阵。

将式(3)转换为整体刚度矩阵,即有限元平衡方程

[K]{T}={Q}

(4)

2.2 仿真分析前处理

前处理工作包括模型导入、网格剖分、定义材料属性、施加边界条件等。以再生粗骨料体积分数45%为例,将MATLAB生成的模型导入COMAOL中,装配联合体。采用基于Delaunay算法的三角剖分概念对再生混凝土模型进行单元划分,划分结果如图3所示。该模型共包含1 519 502个单元,127 848个边界单元。最大单元为 6.7 mm,最小单元为0.03 mm,最大单元增长率为1.3。

图3 再生混凝土模型网格划分

参考TC1100型平板法导热仪工作环境施加边界条件,即第一类边界条件(Dirichlet边界条件),热荷载加载如图4所示。模型内部初始温度25 ℃,左右两侧边界定义为绝热,不与外界进行热交换。上下两边界分别设置50 ℃的热板和20 ℃的冷板。

图4 数值模型边界条件

2.3 五相热导率的标定

再生混凝土的细观成分与普通混凝土相比较为复杂,本文将再生混凝土视为由新硬化砂浆、再生粗骨料构成,其中再生粗骨料包含天然骨料、新界面过渡层、旧界面过渡层和旧附着砂浆。在进行稳态热传导分析之前,需要确定各组分的热导率,新硬化砂浆、天然骨料的热导率可参考具体试验测量结果。以下主要介绍旧附着砂浆、界面过渡层热导率的推导过程。

(1)旧附着砂浆。

大量试验数据证明[15],旧附着砂浆相比新硬化砂浆有较高的孔隙率,内部结构也更加疏松,本文将旧附着砂浆热导率取为新硬化砂浆热导率的80%。

(2)界面过渡层。

朱丽华等[15]指出,新界面过渡层孔隙率高达50%,旧界面过渡层内部构成更为疏松,因而孔隙率更高。本文假定新界面过渡层内部孔隙体积占50%,新硬化砂浆与旧附着砂浆体积各占25%。旧界面过渡层内部孔隙体积占70%,天然骨料与旧附着砂浆各占15%。根据串联模型可求得新、旧界面过渡层的热导率

(5)

(6)

式中:λNCEM、λOCEM分别为新硬化砂浆、旧附着砂浆热导率;vNCEM、vOCEM分别为新硬化砂浆、旧附着砂浆体积分数;λAGG为天然粗骨料热导率;vAGG为天然粗骨料体积分数;λP为孔隙热导率,取0.026 W/(m·K)[18];vP为孔隙体积分数。

2.4 再生混凝土热导率的求解

本文模型采用COMSOL中的PARDISO求解器求解式(4)有限元平衡方程。赋予模型各组分热导率,应用固体传热模块进行热传导数值模拟。在达到稳态热传导后,可以得到再生混凝土温度场、等温线以及热流线分布图,如图5所示。

(a) 稳态温度云图

(b) 热通量流线图

(c) 等温线图图5 再生混凝土热传导云图

由图5可见,再生粗骨料的存在导致等温线出现了不规则的弯折。这是由于再生粗骨料的热导率高于水泥砂浆,热流在流经再生粗骨料时受到的阻力较小。根据最小热阻理论,热量倾向于选择沿着热阻最小的路径传递,因此热流线会在再生粗骨料处发生弯折。

在派升值界面,可通过表面积分计算出模型上下界面的总传导热通量以及温度梯度,进而计算出热流密度,代入式(1)可计算再生混凝土的热导率。

2.5 模型验证

计算热导率常用的理论模型有串联模型、并联模型以及Maxwell模型[16],其计算公式为

λ=v1λ1+v2λ2

(7)

(8)

(9)

式中:λ为再生混凝土热导率;λ1为连续相热导率(新硬化砂浆);λ2为分散相热导率(再生粗骨料);v1为连续相体积分数;v2为分散相体积分数。

为验证本文稳态热传导数值模型的普适性和有效性,分别选取普通混凝土[16-17]、再生混凝土[18]热导率试验值作为对照。考虑到试验过程中部分试件处于孔隙水饱和状态,数值模拟中忽略接触热阻的影响[16]。本文数值模拟结果与文献[16-18]试验结果对比如图6所示。

(a)

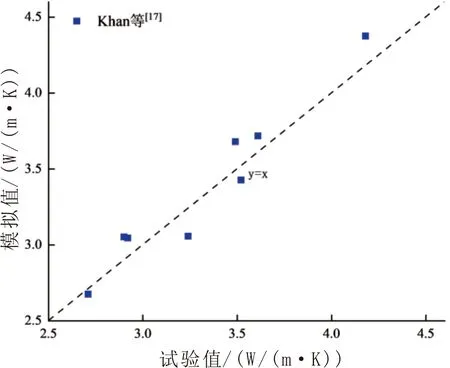
(b)图6 本文数值模拟结果与文献[16-18]试验结果对比

此外,为了体现本文模型的优势,选取文献[18]中再生粗骨料取代率为100%的6组再生混凝土试块,编号分别为A1、A5、B1、B5、C1、C5,将这6组再生混凝土热导率试验结果与本文数值模拟结果以及理论模型预测值进行对比。对比结果如表1所示,括号内为本文数值模拟结果、理论模型预测值与试验结果的相对误差。

表1 再生混凝土热导率试验结果[18]与本文数值模拟结果、理论模型预测值对比 W/(m·K)

由图6可知,本文数值模拟结果与普通混凝土及再生混凝土热导率试验结果吻合度较好(数据点越贴近y=x表明试验结果与模拟结果越吻合)。由表1可知,串联模型、并联模型、Maxwell模型预测值与文献[18]再生混凝土热导率试验结果的平均相对误差分别为9.05%、12.94%、5.41%,而本文数值模拟结果与试验结果平均相对误差仅为3.62%,整体上看优于上述3种理论模型的预测值。结果表明本文建立的再生混凝土稳态热传导数值模型验证结果较为理想,能够较好地预测再生混凝土热导率。

3 参数分析与讨论

采用数值分析的方法,系统地探究了再生混凝土中粗骨料含量、界面过渡区厚度、分散相热导率对再生混凝土热传导的影响。再生混凝土中各热相导率由2.3小节计算得出,其中天然粗骨料、旧界面过渡层、旧附着砂浆、新界面过渡层以及新硬化砂浆的热导率分别为2.487 W/(m·K)、0.574 W/(m·K)、1.220 W/(m·K)、0.669 W/(m·K)、1.525 W/(m·K)。

3.1 再生粗骨料体积分数

为研究再生粗骨料体积分数对再生混凝土热传导性能的影响,对6组不同再生粗骨料体积分数(0%、10%、20%、30%、40%、50%)的再生混凝土模型进行稳态热传导模拟。考虑到再生粗骨料的随机分布,每个体积分数生成5个模型,取其平均值进行传热分析。有限元分析过程中,设置新、旧界面过渡层厚度为60 μm,旧附着砂浆厚度为100 μm。再生粗骨料体积分数对再生混凝土导热性能的影响如图7所示。

图7 再生粗骨料体积分数对再生混凝土热导率的影响

从图7中可以看出,再生混凝土热导率与再生粗骨料体积分数成正相关。再生粗骨料体积分数由0%依次增加到10%、20%、30%、40%、50%时,相应的再生混凝土热导率依次为1.598 W/(m·K)、1.664 W/(m·K)、1.731 W/(m·K)、1.792 W/(m·K)、1.833 W/(m·K),分别增加了31.0%、36.4%、41.9%、46.9%、50.2%。这是由于再生混凝土中再生粗骨料体积分数占比较大且具有较高的热导率,热导率越高,热量传输的阻力越小,说明再生粗骨料在再生混凝土中的热传导性能起着主导作用,是再生混凝土热传导性能的薄弱环节。

3.2 五相热导率

再生混凝土在宏、细观尺度上被认为由天然骨料、新旧界面过渡层、旧附着砂浆、新硬化砂浆所构成。为了深入探究再生混凝土五相热导率改变对再生混凝土热导率的影响,设置再生粗骨料体积分数为35%,以前文计算的热导率λ以基准,各组分热导率相应的调整为0.6λ、0.8λ、1.2λ、1.4λ,分别进行稳态热传导模拟,其他参数保持不变,结果如图8所示。

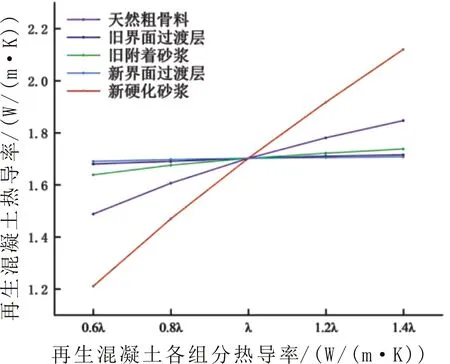
图8 五相热导率对再生混凝土热导率的影响

由图8可知,再生混凝土热导率会随着各组分热导率的提高(降低)而提高(降低),这与复合材料热导率变化规律一致。其中,再生混凝土热导率受新硬化砂浆热导率的影响尤为明显,其次是天然粗骨料、旧附着砂浆、旧界面过渡层、新界面过渡层。这是由于新硬化砂浆在所有细观成分中含量占比最高,当其热导率发生改变,试件热导率也会产生较大的波动。新、旧界面过渡层在整个再生混凝土中含量最少,且热导率小于其他3种组分,因而对再生混凝土热导率影响最小。

3.3 界面过渡层厚度

由于界面过渡层结构的复杂性、质地的疏松以及高孔隙率等特征,其对再生混凝土热工性能的影响不可忽略。为此选定界面过渡层厚度作为变量,对3种再生粗骨料体积分数(20%、35%、50%)下不同界面过渡层厚度(0.02 mm、0.04 mm、0.06 mm、0.08 mm、0.10 mm)的再生混凝土进行研究,其他参数保持不变,结果如图9所示。

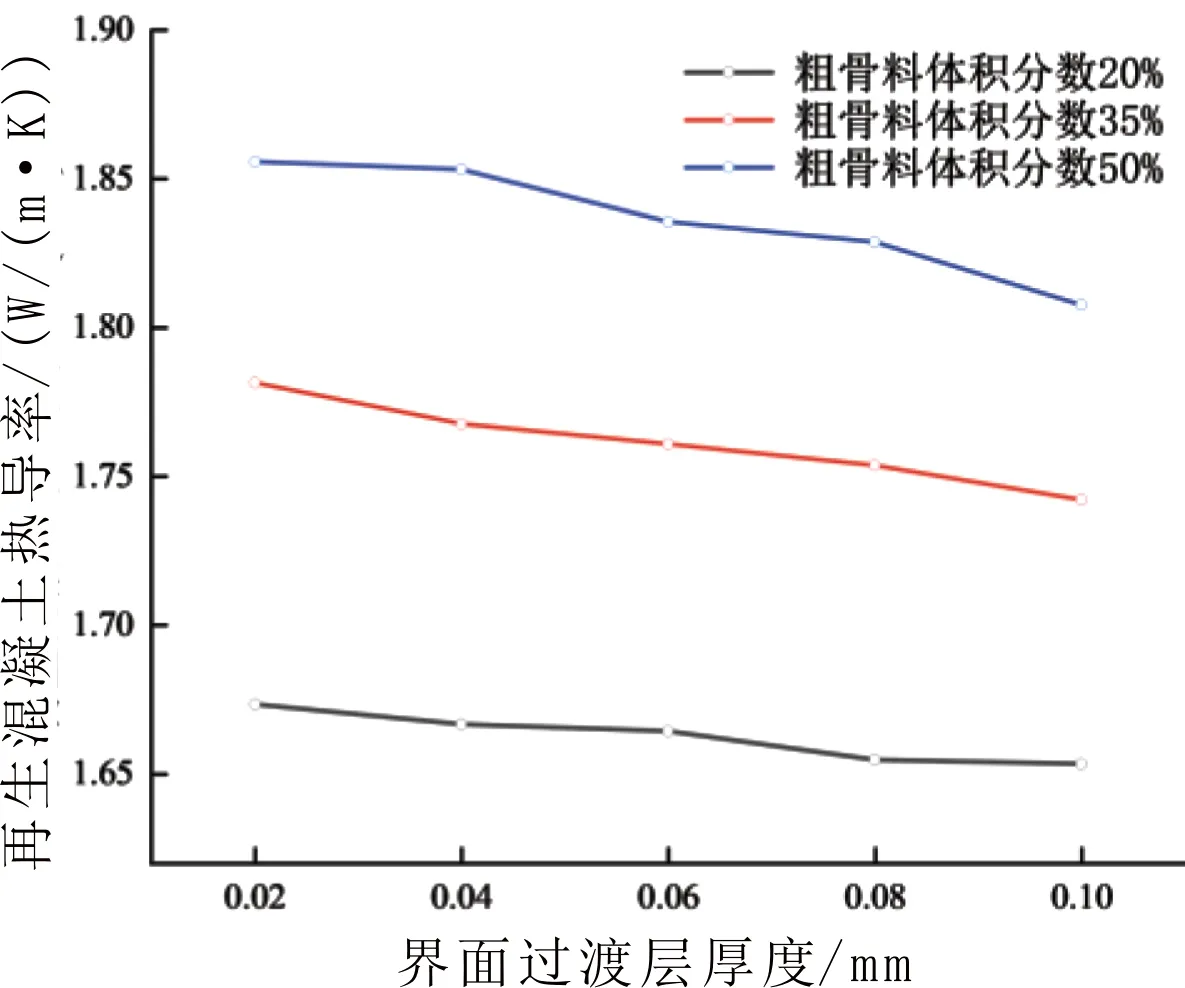
图9 界面过渡层厚度对再生混凝土热导率的影响

由图9可知,再生混凝土热导率随着界面过渡层厚度的增大而逐渐降低。由于界面过渡层内部疏松多孔、空气体积占比较大,有效地阻断了原始热流的传输速度,从而使再生混凝土热导率降低。此外,当粗骨料含量为50%时,再生混凝土热导率下降最为明显;当界面过渡层厚度由0.02 mm分别增加到0.04 mm、0.06 mm、0.08 mm、0.10 mm时,再生混凝土热导率分别降低了0.14%、1.08%、1.45%、2.59%,幅值可达18倍。原因是界面过渡层附着在天然粗骨料的外围,再生粗骨料体积分数的增加导致界面过渡层所占比重显著增加,再生混凝土热导率进一步减小,因此分析界面过渡层对再生混凝土热工性能的研究尤为重要。

4 结论

基于细观层次建立包含天然粗骨料、旧界面过渡层、旧附着砂浆、新界面过渡层、新硬化砂浆的二维五相模型,通过MATLAB与COMSOL联合仿真的方法建立再生混凝土稳态热传导数值模型,并与已有文献试验结果进行对比,平均误差仅为3.62%,且误差小于3种常用的理论模型预测值,模型可信度较高,表明利用数值模拟的方法研究再生混凝土热工性能是可行的。

再生粗骨料体积分数的增大会提高再生混凝土热导率,促进了热量的传输,极大程度上影响再生混凝土的热工性能,不利于提高再生混凝土的保温隔热能力;再生混凝土热导率受五相成分共同作用,其中新硬化砂浆的影响效果最为显著。

旧界面过渡层是再生混凝土与普通混凝土在传热性能方面产生差异的主要原因。界面过渡层厚度的增加可以降低再生混凝土热导率,有效提高再生混凝土保温隔热能力,对推广再生混凝土应用有较大意义。