例谈三角最值问题

蒋 伟

扬州大学附属中学 (2205002)

三角一直是高考的重点考察对象,解三角形中的最值问题更是高频考点,因为它易于和其他知识进行交汇,全面考察学生的数学素养,培养学生分析问题和解决问题的能力.解三角形是由已知的边角确定未知边角元素的过程．而正、余弦定理的作用就是将边角间的关系数量化,从而构建方程(或方程组),因此方程思想是解三角形的关键．如果已知的方程个数比未知的边角元素个数少,这样就变成不确定三角形,此时就可以研究三角形中的最值(范围)问题．本文从知识、能力、方法三个维度去处理三角形中的最值问题,特别是方法维度从多个角度解决问题为学生指明方向,极大地培养了学生的数学素养.

点评：从知识维度看第二问考察了边的最值,本质是考察角度的最值,从能力维度看属于多变量经过减元变为单变量角B的式子的最值,运用的方法为基本不等式解决最值问题.

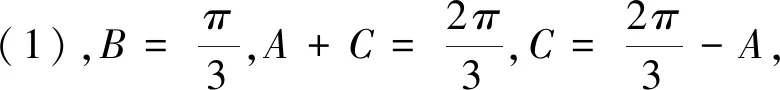
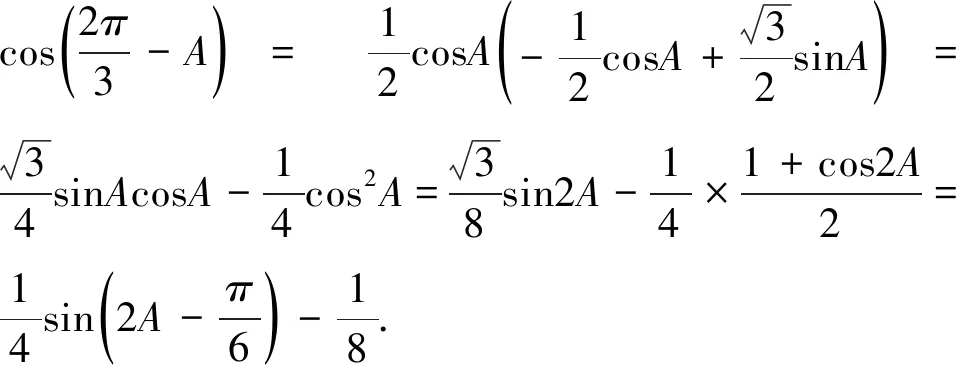
点评：第二问从知识维度看考察了角的范围问题,从能力维度看属于多变量经过减元变为只有角A的三角函数的值域问题,运用的方法为函数思想解决范围问题.

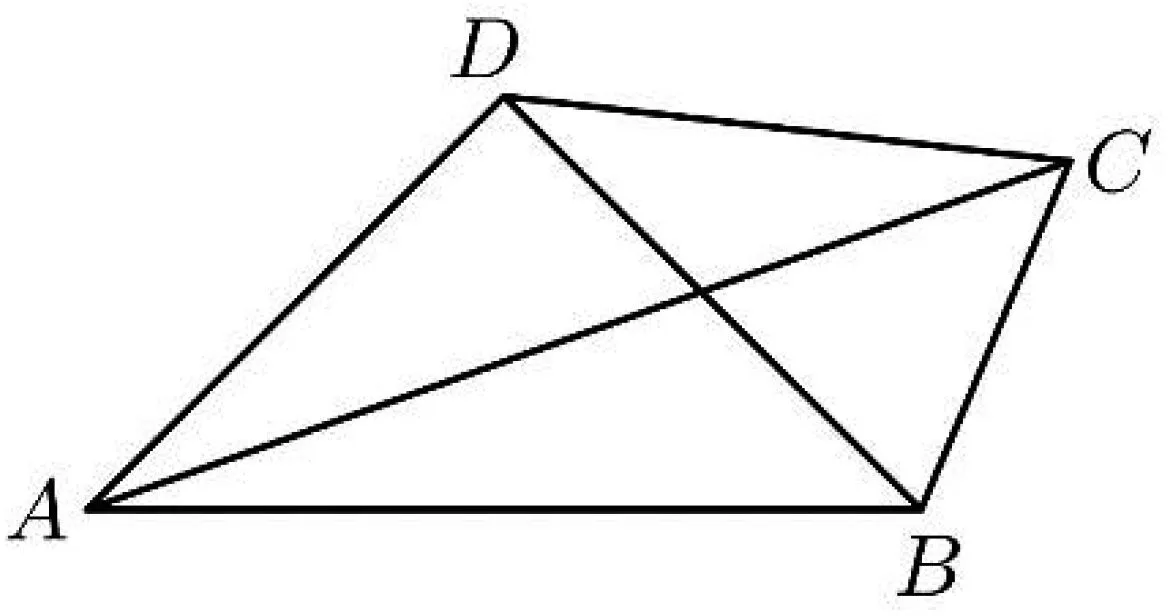
图1

解析：(1)略;(2)法一：(正余弦定理选择角度作为变量)设∠BCD=θ(0<θ<π),在△BCD中,由余弦定理得BD=

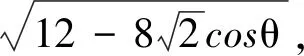
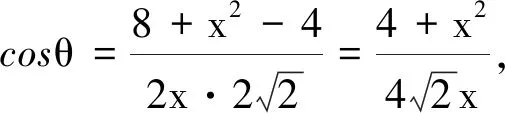
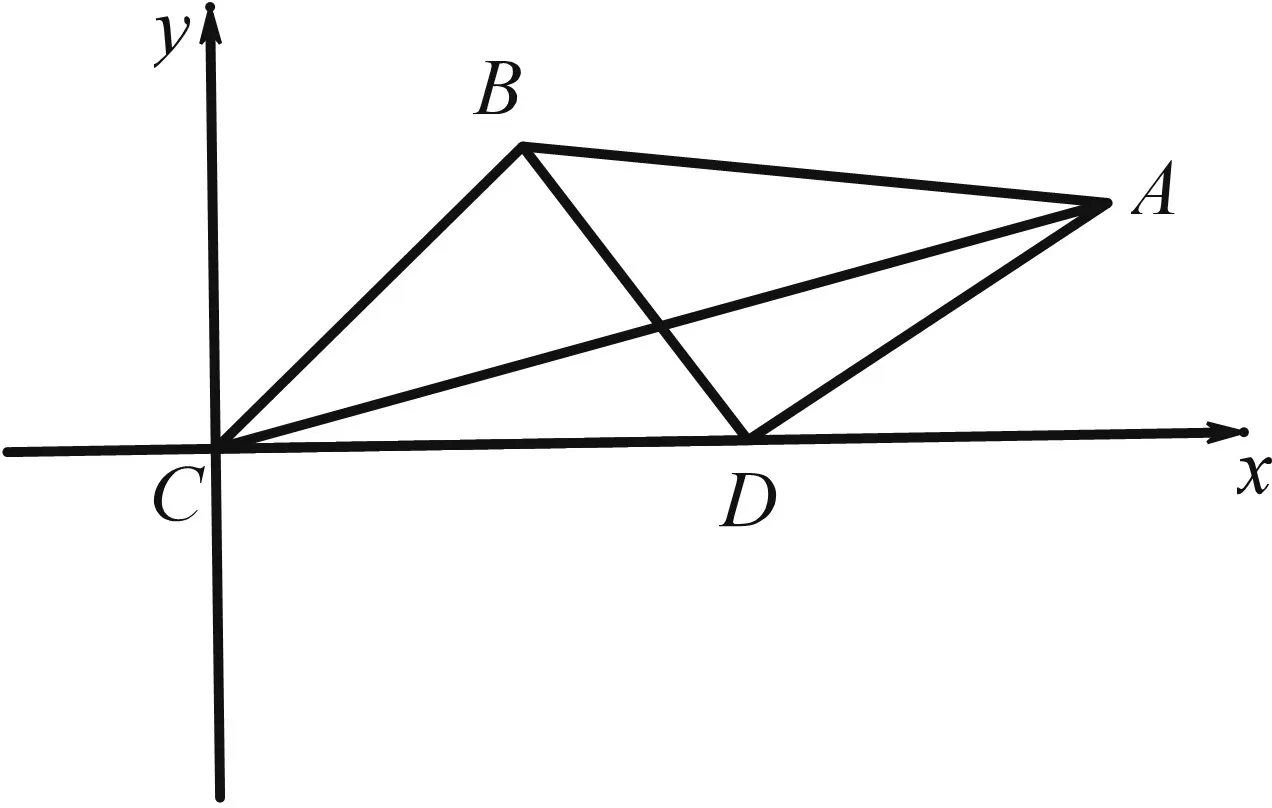
图2

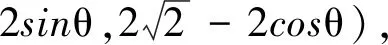
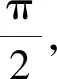
图3

点评：第(2)问从知识维度看考察长度的最值,学生建模比较困难,如果以边作为自变量,很难用导数计算正确,选择角度作为变量,思维要求比较高.

题4 如图4,在△ABC中,若AB=AC,AD=DC,BD=3.(1)求△ABC面积的最大值;(2)求△ABC周长的最大值.

图4

我们先求面积的最大值问题.

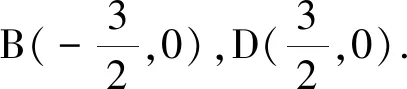
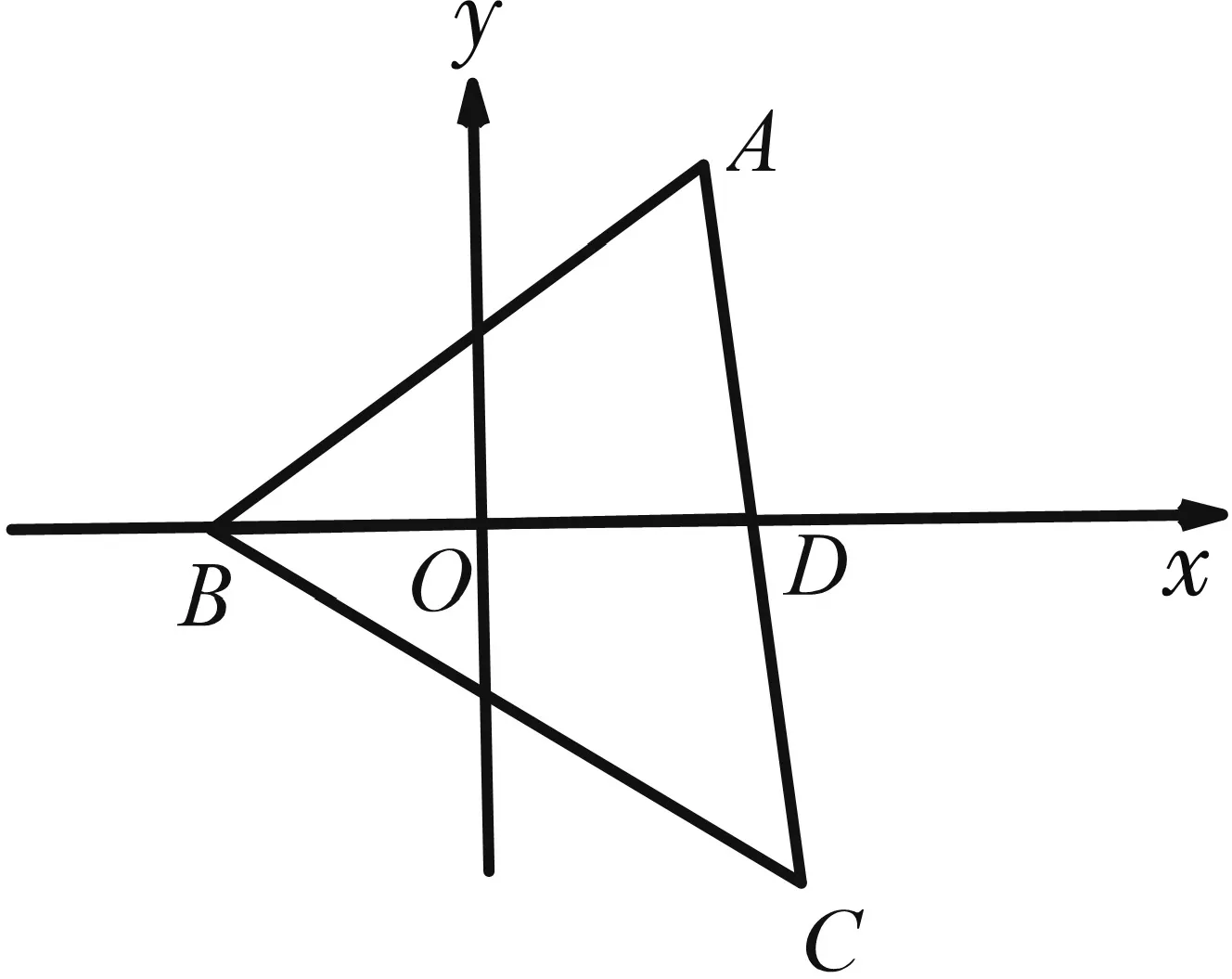
图5

现在处理第(2)问

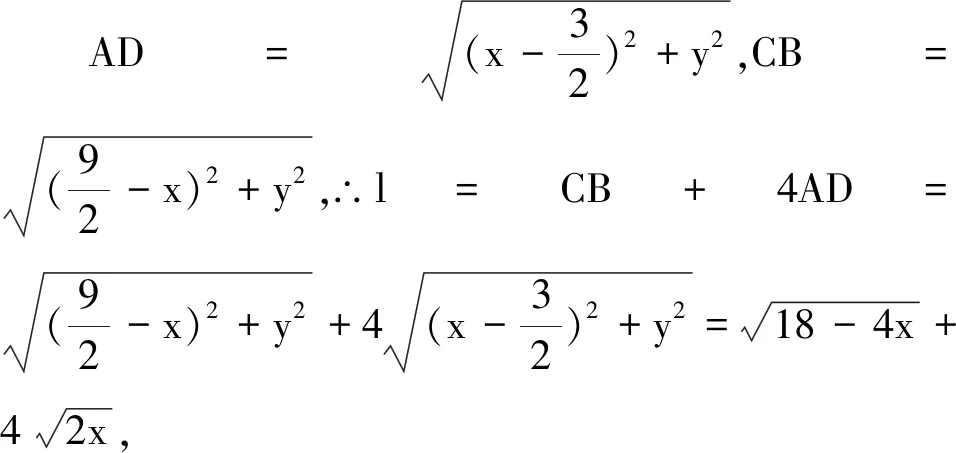
点评：从知识维度看考察长度的最值,从能力维度看属于双变量的最值问题,难度较大;从方法维度来看,选择运动轨迹思想,能较快解决问题,第一问隐含了圆方程,第二问隐含了椭圆方程.

结语在解决三角形中的最值问题时,我们要时刻提醒从三个维度去考虑问题,熟练运用正余弦定理、向量、解析思想转化为函数、基本不等式、运动轨迹问题,从而找到问题的突破口.