基于预测控制的活塞式压力计活塞位置平衡技术

林 佳 伟, 杨 林, 卜 繁 岭, 樊 双 蛟, 何 贞, 高 腾

( 大连工业大学 机械工程与自动化学院, 辽宁 大连 116034 )

0 引 言

活塞式压力计是目前唯一能在宽量程范围内溯源至SI基本单位的压力计量仪器[1],其压力变化范围越大,对于活塞平衡的控制要求越高[2]。

目前应用于活塞平衡系统的控制算法主要有PID控制、LQR控制、自抗扰控制、自适应控制等。由于PID控制简单,大多数平衡系统采用PID及其改良算法控制,如赵杰等[3]的串级算法、王欣[4]的位置式算法、魏波[5]的微分先行算法等。这些算法对参数的依赖性较大,大多数应用在线性系统,对于初始参数要求比较高,自适应能力比较差[6],一旦初始参数变化就会出现振荡等问题,并且属于单输入、单输出算法,调整时间较长。

刘建春[7]针对压力仪表的准确度、可靠性等易受使用环境、使用频繁程度及保养、存放条件的影响的情况,对常规活塞式压力计的结构和工作方式做出了改进,建立了压力计内部模型,使用位置式PID和增量式PID[8]对活塞浮起稳定状态和超调进行控制,实现了较好的效果。这两种算法计算的是输出增量,动作误差较小,但是存在静态误差,影响总体时间响应。随着压力的增加和检定活塞直径的减小,PID算法在低压和高压阶段表现出来的性能差异较大。

LQR控制算法的问题主要是稳定性和抗干扰性不强。模糊控制与LQG算法相结合也具有较强的实践可行性[9],但该算法需要准确的数学模型,才能有效改善控制效果。基于DQN算法、PG算法[10]在控制稳定性方面依赖更多的训练回合和时间,并且只适用于简单系统。何军虎等[11]提出基于参数优化的自抗扰技术,抗干扰能力一般,对参数选择有较高要求。

广义预测控制算法(GPC)是一种在自适应控制研究中发展起来的一类预测控制算法[12],该控制算法对模型精度要求低,对参数化模型的阶次不敏感,并且在其性能指标中引入控制增量加权系数,提高了系统闭环稳定性。

本研究以250 MPa全自动活塞压力计为研究对象,提出了基于GPC[13-14]的新型控制技术,结合高压活塞浮起位置平衡的特点,考虑了各种影响活塞平衡的因素,并将这些因素作为变量输入系统,通过受控自回归积分滑动平均模型进行方程的计算,得到调整量,达到活塞的快速稳定。

1 基于GPC算法的压力计活塞平衡控制

全自动活塞式压力计整体构造由自动加载系统部件(图1,部件1～4)和自动造压系统(图1,部件5～9)组成。全自动活塞式压力计基于帕斯卡、流体静力学原理来实现压力计量,检定活塞和砝码组件(承重盘、专用砝码)的总重量所产生的压力与传压介质所产生的压力相平衡。

1 砝码; 2 承重盘; 3 检定活塞; 4 活塞筒; 5 高度传感器; 6 显示器; 7 压力表; 8 驱动活塞; 9 驱动电机

活塞压力计在压力检定过程中,活塞位置的变化受到控制压力、介质泄漏、活塞有效面积、温度等多个变量的影响。因此,在稳压读数过程中很难使活塞稳定在活塞浮起位置的平衡点。通过控制这些变量预测活塞的行为,从而达到快速稳定的平衡过程是改善控制品质的重要途径。

活塞式压力计输入输出模型如图2所示。输入变量为驱动活塞行程,扰动变量为温度、检定活塞有效面积。输出变量为活塞高度。高度传感器主要用于测量活塞的浮起高度。

图2 输入输出模型Fig.2 Input-output model

2 压力计检定活塞模型建立

活塞式压力计质量与压力转换如式(1)所示。

p=mg/A0

(1)

式中：m为加载时砝码的质量,g;A0为活塞横截面积,mm2;p为压力计工作时压力介质作用在活塞底端的压强,MPa。活塞压力计计量原理如图3所示。

图3 活塞压力计计量原理Fig.3 Measuring principle diagram of piston manometer

液体产生垂直向上的力F=pA0。经过对活塞压力计内部及流体静力学研究分析,设计出压力计机理模型,如式(2)所示。

(2)

式中：H1为驱动活塞进给量,mm;D为驱动活塞的直径,mm;H2为检定活塞升降高度,mm;α=αp+αe,αp、αe为检定活塞和活塞缸热膨胀系数,℃-1;tp为实验温度,℃;λ为检定活塞的形变系数;pp为检定压力点压力,MPa。

系统所用执行器为伺服电机,该电机接收上位机传送的活塞高度值信号。根据式(2)计算的检定活塞高度与传感器检测高度进行比较,通过算法模型优化计算,把信号传递给电机进行实时控制,改变转速,通过螺母旋转带动丝杠运动加压。如图4所示,当脉冲范围在25～30 kHz时,检定活塞受变量影响,上升高度呈现不稳定状态。电机脉冲与驱动活塞进给量呈线性关系,电机脉冲达到30 kHz,电机转动100圈,通过减速箱增加扭矩,驱动活塞进给量为4 mm,检定活塞高度呈稳定状态。

图4 电机脉冲与活塞进给量和高度关系Fig.4 Relation between motor pulse and piston feed and height

3 广义预测控制算法及控制器设计

广义预测控制算法采用受控自回归积分滑动平均模型(CARIMA),对于受多变量影响的压力计系统,如式(3)表示。

(3)

式中：z为算子;A、B、C为z的多项式;z-1为后移算子,表示一种递推关系;Δ=1-z-1为差分算子;k为时延步数;ε(k)为零均值噪声;y(k)为输出向量;u(k)为输入向量。

(4)

由于ε(k+j)是噪声产生的未来响应,一般无法预测,两边同乘Ej(z-1)Δzj,由式(4)丢番图方程推导得出系统(k+j)步广义预测控制的预测模型,广义最优预报如式(5)表示。

y(k+j)=Fjy(k)+GjΔu(k+j-1)

(5)

假设活塞压力计活塞高度为输出变量Y(k),驱动活塞行程为输入变量U(k),活塞有效面积、传压介质温度分别为扰动变量,通过建立如图5模型来优化检定活塞高度变化。

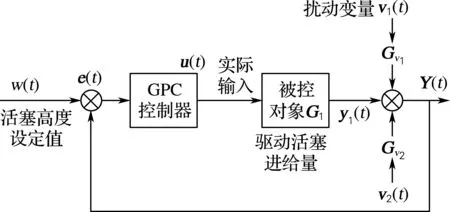
图5 活塞高度变化优化模型Fig.5 The optimization model of piston height change

由式(3)和图5可得出输入u到输出y之间的z传递函数,G1(z-1),Gv1(z-1),Gv2(z-1)分别为活塞行程、活塞有效面积变化、传压介质温度变化多项式,各控制对象的传递函数形式如式(6)所示。

(6)

由图5可得到活塞高度变化模型关系式满足式(7)。

y(k)=y1(k)+yv1(k)+yv2(k)

(7)

式中：y(k)为系统输出;y1(k)为活塞行程输出;yv1(k)为活塞有效面积;yv2(k)为传压介质温度。

可以得到式(5)中A(z-1),B(z-1),U(k-1)矩阵,其中输出y是1×1矩阵,输入u是3×3矩阵,具体如式(8)所示。

(8)

通过对多有影响因素分析,由实验数据和模型计算辨识得到系统整体的传递函数,其中输入、输出信号都是活塞高度,离散化后的传递函数如式(9)所示。

(9)

由式(3)可以得到A(z-1)=1-1.806z-1+0.832 5z-2,B(z-1)=0.001 28z-2。

由丢番图方程得到的式(5)广义预测控制策略,在此基础上引入一个代价函数式(10)进行算法闭环优化。

(10)

式中：J为优化性能指标,E为期望值,Nμ为控制步数,N1为起始预测值,其中u1=y(k+j)-yr(k+j),u2=λΔu(k+j-1),λ为控制增量权系数。广义控制算法是根据当前和未来控制效果跟随控制策略预测活塞行为,其中y(k+j)采用柔化的参考轨迹形式,其中j=1,…,N,N为预测步长,0<α<1按式(11)表示。

yr(k+j)=αyr(k+j-1)+(1-α)wr

(11)

其中,y为实际输出值,yr为期望输出值,wr是系统控制目标值。预测第j步参考轨迹形式由式(12)表示,j=1,…,N即

yr(k+j)=αjy(k)+(1-αj)wr

(12)

(13)

令∂J/∂Δu=0,且Nμ=N时,令j=3,计算出Δu,然后更新数据,其中y1=y(k+j)-yr(k+j),进行下一步预测。令u3=b1ej,j-1Δu(k-1),y2=fj,0yr(k)+fj,1yr(k-1)得式(14)。

(14)

其中b1=0.001 28,yr(k+1)=0.512yr(k)+(1-0.512)wr,控制输出如式(15)所示。

u(k)=u(k-1)+Δu(k)

(15)

由式(14)可知,当j=30时,令k=k+1预测至(k+30)这一步。

算法控制流程如图6所示。

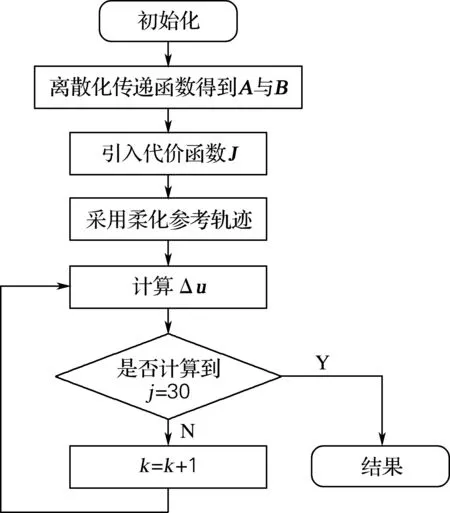
图6 算法控制流程图Fig.6 Flow chart of algorithmic control

4 仿真分析

实验使用的压力计是校企联合研发的高压(250 MPa)全自动活塞式压力计。实验参数见表1。应用MATLAB进行模型参数辨识和仿真,根据多次仿真实验,调整预测步数和控制长度之间的关系来控制活塞稳定状态,并与PID算法比较来验证该算法的有效性。

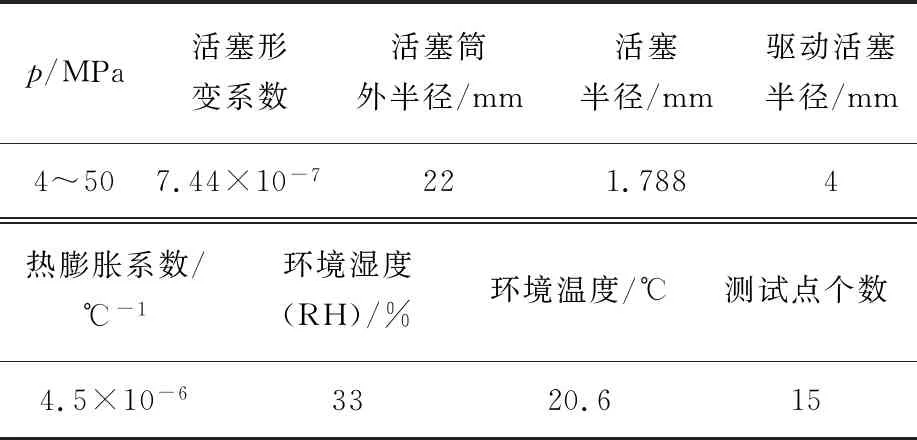
表1 活塞压力计参数Tab.1 Parameters of piston manometer

仿真实验中,设置活塞初始高度为0,GPC算法中α=0.8,wr=1 mm。

增量式PID控制算法如式(14)表示。

Δu(k)=Kpe1+Kie(k)+Kde2

(14)

式中：令e1=e(k)-e(k-1),e2=e(k)-2e(k-1)+e(k-2),其中e为偏差;Kp为比例系数;Ki为积分系数;Kd为微分系数。

设置PID参数Kp=10,Ki=3,Kd=3;GPC算法参数为j=100,λ=0.1。仿真实验比较活塞稳定高度变化其输出结果如图7所示。由仿真结果可以看出GPC控制下的系统调节时间在67 s左右趋于设定值,活塞高度变化趋于稳定,达到读数稳定性要求。PID控制下的系统调节时间在80 s左右趋于设定值,并且GPC的响应时间较PID也更快达到设定值。

图7 Ki=3时活塞稳定高度变化Fig.7 Verification of piston stability height with Ki=3

图7所示的两种算法仿真从60 s开始响应时,GPC的响应速度较快,通过调节PID的参数加快其系统响应速度,GPC仿真参数保持不变。PID参数调节为Kp=10,Ki=9,Kd=3,仿真结果如图8所示。

图8 Ki=9时活塞稳定高度变化Fig.8 Verification of piston stability height with Ki=9

由仿真结果可以看出,当两者趋于设定值的快速性相同时,PID以64 s较快的响应速度趋于设定值,这时活塞趋于稳定。在稳压过程中,PID控制的活塞稳定性出现了较大的超调,活塞上下浮动状态明显,说明未达到读取数值稳定性的要求,继续调节,达到稳定状态的时间较GPC更长,效果差。

由图9 GPC控制活塞高度变化的有效性可以看出,黑色曲线预测步长设定8,控制长度设定1,当仿真步数设定500步时,预测步长和控制长度比值过大,响应时间延迟达到200步趋近设定值,而后偏离稳定状态,稳定效果不理想。减少两个参数的比值,仿真结果可以看出,预测步长选择30,控制长度选择21达到了最佳控制效果,符合实验要求,可以稳定90步时间。在多次实验增加预测步长和控制长度的大小,实验结果与预测步长选择30,控制长度选择21相似,所以选择该结果作为实验最佳输出。从仿真结果可以得出预测步长N和控制步长Nu的选取,对系统动态性能有直接影响,N选大些,Nu选小一些,有利于系统的稳定;但N与Nu之间的比例关系不能过大。比例过大后,系统的跟踪性能变差,动态效果也变差。N与Nu的比例关系变小时,动态性能效果和跟踪性能趋近稳定,能够最大限度减少不稳定状态,同时也证明了GPC算法控制的活塞高度变化的有效性。

图9 GPC控制活塞高度变化的有效性Fig.9 GPC control for the effectiveness of piston height changes

设置PID参数Kp=60,Ki=30,Kd=3;GPC参数根据图9仿真结果调整为j=30,λ=0.05。算法仿真结果如图10所示。由图10可见,PID较GPC先达到设定值高度,响应速度较快,系统加压10 s左右,活塞上升到最大高度。随着系统稳压过程受不可控因素的影响,出现了较大的超调,活塞高度变化明显,输出变化不稳定,并且活塞高度趋于稳定的调节时间较长,稳态误差较大。GPC控制的活塞高度变化,经过两次超调,在50 s左右趋于设定值。较PID在54 s左右达到设定值时间更快,高度变化满足生产要求,仿真效果较好。由测试数据可以看出,在系统响应60 s后,活塞高度恢复至设定的工作高度后,并不能稳定在一个确定的高度,而是在工作高度附近进行小幅的反复振荡。这也是今后需要更深入研究的方向。

图10 仿真结果Fig.10 Simulation result

5 结 论

以250 MPa全自动活塞式压力计为研究对象,采用广义模型预测控制理论,提出的针对快速稳定达到活塞浮起的位置平衡点的控制算法初步解决了活塞压力计在使用过程中工作环境发生变化对活塞浮动的影响。通过广义预测算法预测了检定活塞行为并进行实时控制。广义模型预测控制对于检定活塞浮起位置的稳定过程具有较好的效果,并且在时间控制上GPC优于PID。

这种基于GPC算法的压力计活塞浮起位置平衡控制方法降低了人为操作与反应条件的波动,从而达到减少能源和设备损耗、最大限度地发挥装置的应用能力,为用户创造更大的经济效益。