基于灵敏度分析的双塔斜拉桥有限元模型修正优化

张 倩, 薛小强, 徐焱强

(1.成都理工大学 环境与土木工程学院, 成都 610059; 2.四川兴蜀工程勘察设计集团有限公司, 成都 610072)

“灵敏度”概念的提出[1],推动了国内外学者对基于参数灵敏度的有限元模型修正方法的研究。目前,有限元模型修正中对灵敏度参数选择[2-4]和参数灵敏度分析[5-6]的研究日趋成熟。在选择合适的灵敏度参数后筛选合适的修正参数,通过灵敏度分析去掉影响低的参数,从而确定正确的修正函数和变量[7-8]。修正结构材料参数,使修正后的有限元模型结构振动响应特性与实际结构试验响应测量值相符[9]。学术界也从多个角度[10-12]不断改进和完善了模型修正技术。而大跨度斜拉桥模型结构和边界复杂,有限元模型与实际误差较大,目前尚未有从结构响应和修正精度的角度,对比基于静力、动力及联合静动力的有限元模型修正方法的精确性研究。

苏通长江大桥是我国综合建设条件最复杂的大型桥梁工程之一,建立一个精准的有限元模型非常重要。为此,本文以苏通长江大桥为工程背景,分析斜拉桥各参数的敏感性,并基于静动载试验数据探究静、动力及联合模型修正方法以及模型修正前后结构响应和修正参数上的差异,为桥梁结构日常检修、损伤识别和桥梁结构安全状态评估等提供参考依据。

1 模型修正优化方法

模型修正基本方法分为矩阵型修正法和设计参数型修正法。矩阵型修正法计算效率高,但存在破坏有限元模型连续性的可能性,从而影响整体修正精度。设计参数型修正法通过构造静、动力响应特性目标函数后修正结构参数,使有限元结构模型与实际结构目标函数最小化以达到修正的目的[13]。构造的函数一般是非线性,故采用迭代法对目标函数进行优化,并将优化问题转化为间接线性问题求解[8],修正后的模型物理意义较明确,且模型设计参数与工程结构参数易对比。因此,本文采用设计参数型修正法对苏通长江大桥有限元模型进行修正。

设计参数型修正法选择待修正参数后,有限元模型修正问题变成结构待修正参数优化问题。其原理是构建问题目标函数,运用优化算法进行一定要求下的参数迭代运算和灵敏度分析,求解使目标函数极小值的修正参数最优解问题[14]。常用的优化求解方法有ANASY软件中的零阶和一阶算法及MATLAB优化工具箱中fmincon函数中的序列二次规划法。一阶算法较零阶算法精确,但迭代时间更长[15]。因此,本文选用序列二次规划法进行模型优化。二次规划问题指优化目标函数是二次函数,约束为线性等式或线性不等式条件。序列二次规划法就是通过解一系列二次规划问题,从而产生收敛于优化问题的参数最优解和Lagrange乘子的迭代序列。

本文运用MATLAB优化工具箱中有约束的非线性最小化函数(fmincon)进行模型静动力目标函数和修正参数的迭代优化,最终实现序列二次规划法优化。

2 工程概况

2.1 总体布置

苏通长江大桥主桥为双塔双索面斜拉桥,半漂浮体系。主梁采用扁平钢箱梁,斜拉索共136对,单根拉索最长577 m。主梁与索塔之间设置抗风支座和粘滞阻尼器,过渡墩、辅助墩之间设置纵向滑动支座。粘滞阻尼器只在桥梁超出行程时约束主梁运动。

2.2 桥梁静动载试验

静载试验重点对该桥结构测点位移挠度值进行分析,测点布置如图1所示。动载试验在S1、S2和S4处测试动应力,在S4处挠度测试,测量桥梁结构在移动荷载下静、动力叠加总效应,从而计算静、动力总效应与静力效应的比值。

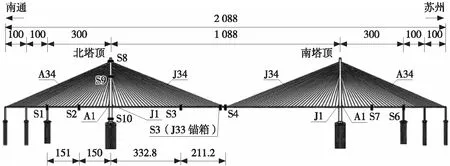
(a) 静载试验测试部位示意

采用环境随机振动法进行振动特性测试,得到结构各部分振动响应数据。

2.3 初始有限元模型建立

用Midas/Civil建立苏通长江大桥主桥的初始有限元模型,如图2所示,共733个节点、698个单元。主桥斜拉桥有限元模型钢箱梁采用Q345qD、Q370qD钢材模拟,斜拉索采用Φ7、抗拉强度为1 770 MPa的钢丝模拟,主塔塔柱采用C50混凝土模拟,辅助、过渡桥墩采用C40混凝土模拟,承台采用C35混凝土模拟,具体特性参数如表1所示。主梁、索塔及桥墩等采用实体梁单元模拟,斜拉索采用桁架单元模拟,且考虑拉索垂度效应。斜拉索与主梁连接采用弹性连接,主塔、过渡墩和辅助墩墩底固结,过渡墩和辅助墩(墩顶)释放梁端竖向约束,并根据实际情况添加荷载工况及移动荷载分析数据。

表1 苏通长江大桥材料特性设计参数

图2 苏通长江大桥有限元模型

2.4 静力特性相关性分析

选择模拟主梁下挠最大、代表性强的工况2(中跨跨中)和工况22(北跨跨中)在静力试验满载时得到的主梁挠度数据,与静载试验实测测点位移值进行比较,结果如表2所示。

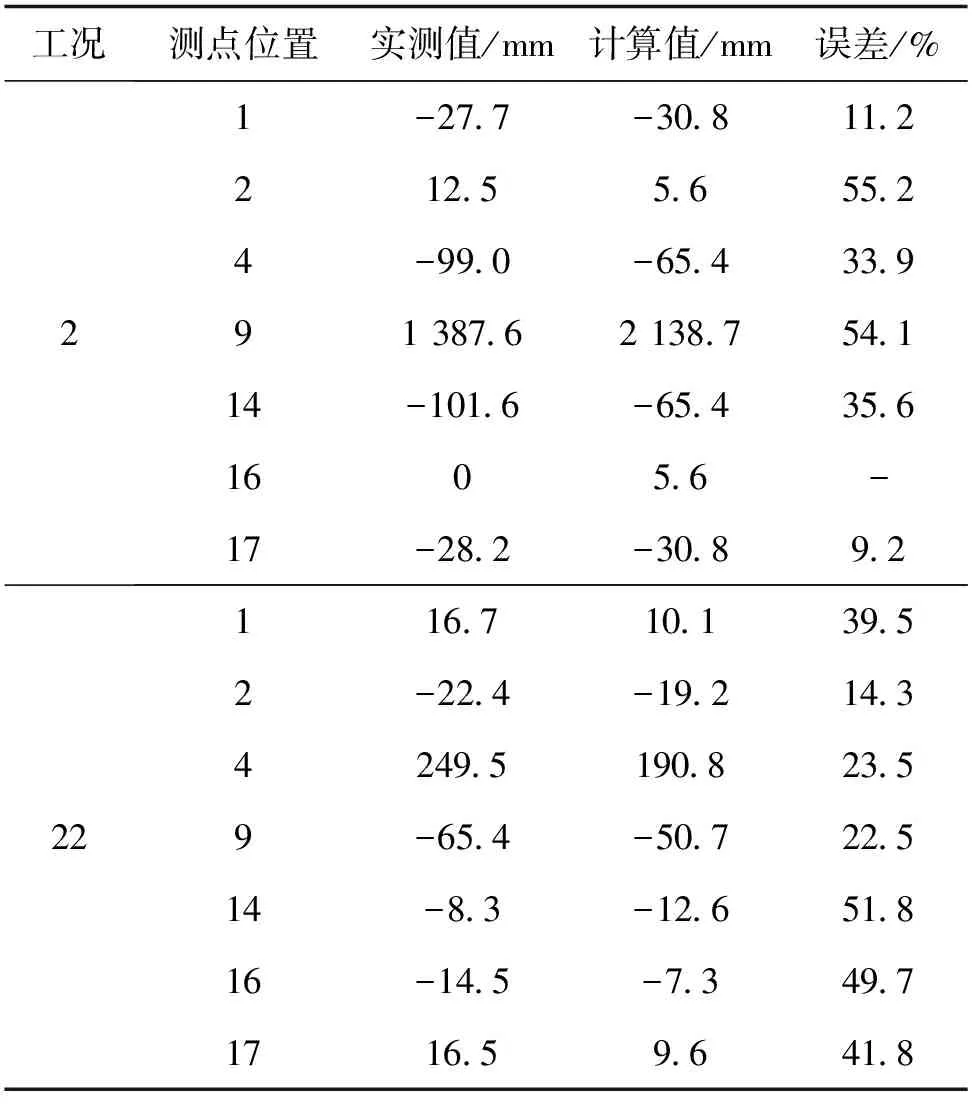
表2 工况2和工况22测点位移结果对比

由表2可知,由于桥梁跨度大、整体柔度高,模型位移与实际位移相差较大,静力特性误差大。因此,不能准确反映实际桥梁状态。

2.5 动力特性相关性分析

以有限元模型结构自振频率计算值和实测值误差衡量频率相关性,计算模态保证准则MAC(Modal Assurance Criterion)衡量阵型相关性,模态参数对比如表3所示。

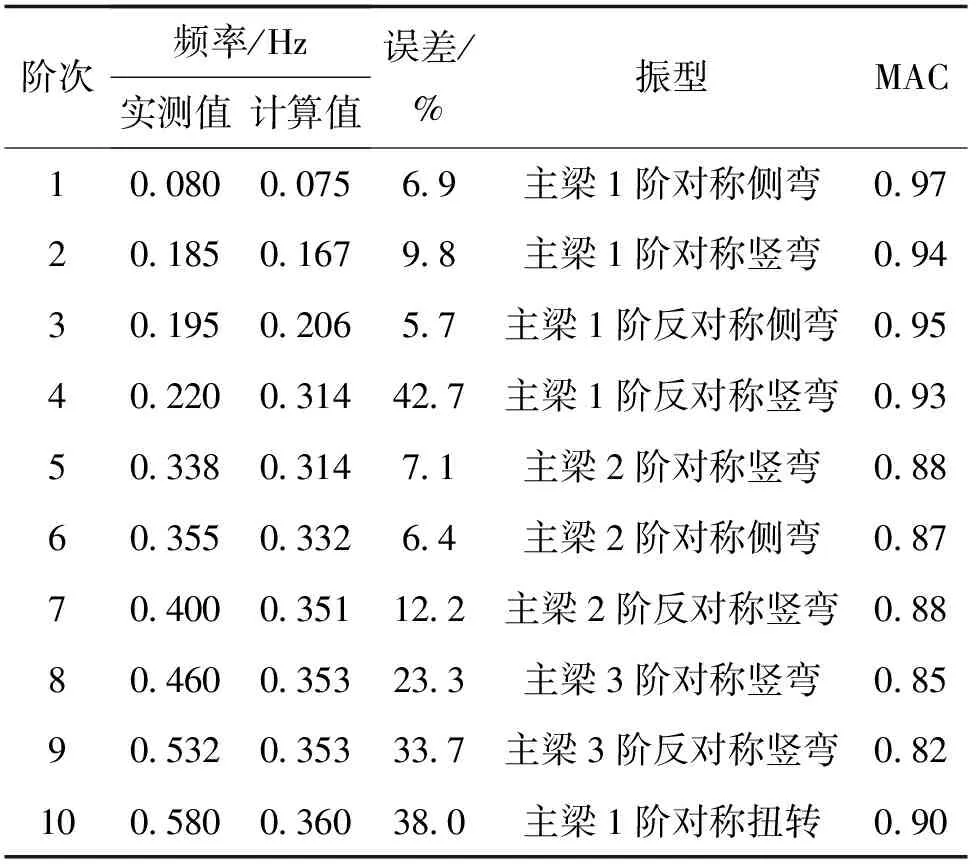
表3 苏通长江大桥模态参数对比

由表3可知,模型动力特性误差较大,因此不能准确反映实际桥梁结构的真实静动力响应状态。

3 模型修正特性灵敏度分析

3.1 静、动态特性灵敏度分析

大跨度桥梁结构复杂,采用有限差分法代替直接求导法进行参数灵敏度计算,修正参数扰动步长取10%。

将静态特性灵敏度分析中主梁各测点位移对主梁各参数灵敏度对比、动态特性灵敏度分析中的模态频率计算对主梁影响较高的要素灵敏度对比按单位量级分开对比,结果如图3和图4所示。

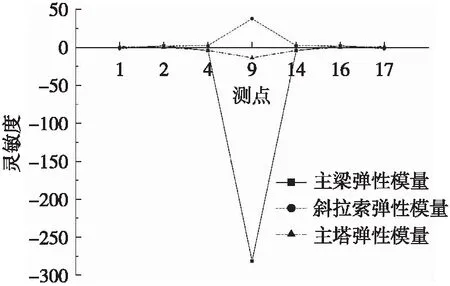
(a) 构件弹性模量灵敏度

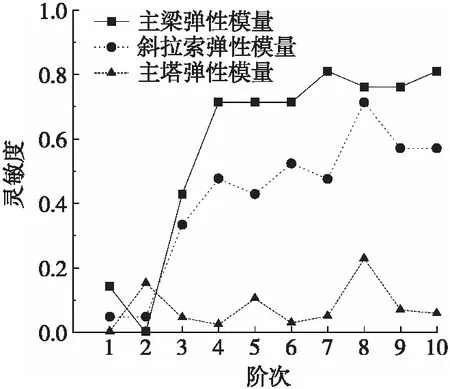
图4 结构模态频率对各修正参数灵敏度对比

由图3、图4可见,结构位移对各修正参数灵敏度规律为:1) 结构材料弹性模量灵敏度:主梁>斜拉索>主塔;2) 结构容重灵敏度:主梁>斜拉索>主塔,且斜拉索面积灵敏度又较主塔容重高。结构模态频率对结构各组成部分弹性模量灵敏度:主梁>斜拉索>主塔。

3.2 参数灵敏度正交分析

为探究结构各组成部分构件参数变化组合敏感度,对主梁、斜拉索、主塔弹性模量考虑各参数变化10%后的试验组合进行正交性试验组合,试验结果如图5～图7所示。

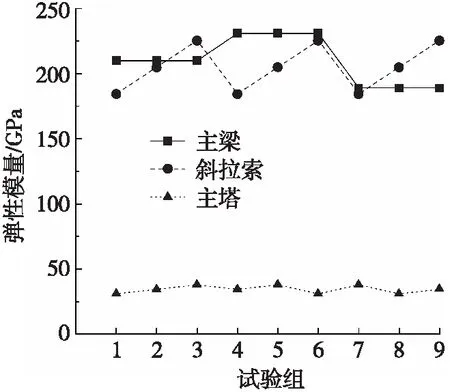
图5 修正参数正交试验

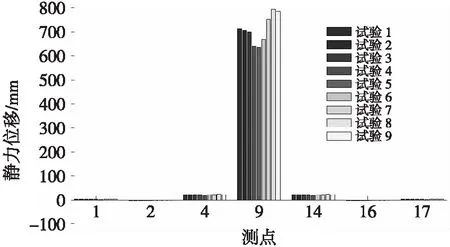
图6 各正交试验各重要测点静力位移对比

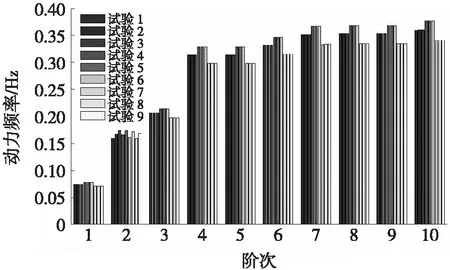
图7 各正交试验动力频率对比

从图5～图7可知,主梁弹性模量对静力位移和动力频率值变化起主导作用:1) 主梁弹性模量增大,主梁位移会相应减小,结构自振频率增大;2) 斜拉索弹性模量增大,主梁位移减小;3) 结构自振频率变化对主塔弹性模量和斜拉索弹性模量变化敏感度较低。

进一步分析弹性模量影响结构静动力响应机理:主梁弹性模量增大,主梁刚度增加,整体变形减小,自振频率增大;斜拉索弹性模量增加,斜拉索变形量减小;主塔弹性模量增大,刚度增大,变形能力减小。

4 模型修正优化

4.1 静力位移模型修正优化

通过建立静力位移目标函数对该斜拉桥有限元模型进行修正,选择5个对静力位移敏感度高的结构参数:主梁弹性模量、容重、斜拉索弹性模量、面积和主塔弹性模量进行有限元模型优化求解,修正参数范围如表4所示。

表4 初步修正参数选择及估值

优化过程如下:1) 将前一次优化后的修正参数变化量带入模型进行下一次位移参数灵敏度分析;2) 将灵敏度结果带入MATLAB优化工具箱进行修正参数求解;3) 对有限元模型结构位移值求解。因非线性最小化函数中的Uti不能为零,故在软件数据组中将工况2的测点16实测位移设为小值进行迭代计算,不等式约束计算位移与实测位移的残差限值取10%。初步修正参数选择及估值如表4所示,模型静力位移修正、模型修正前后参数值对比结果如表5、表6所示。

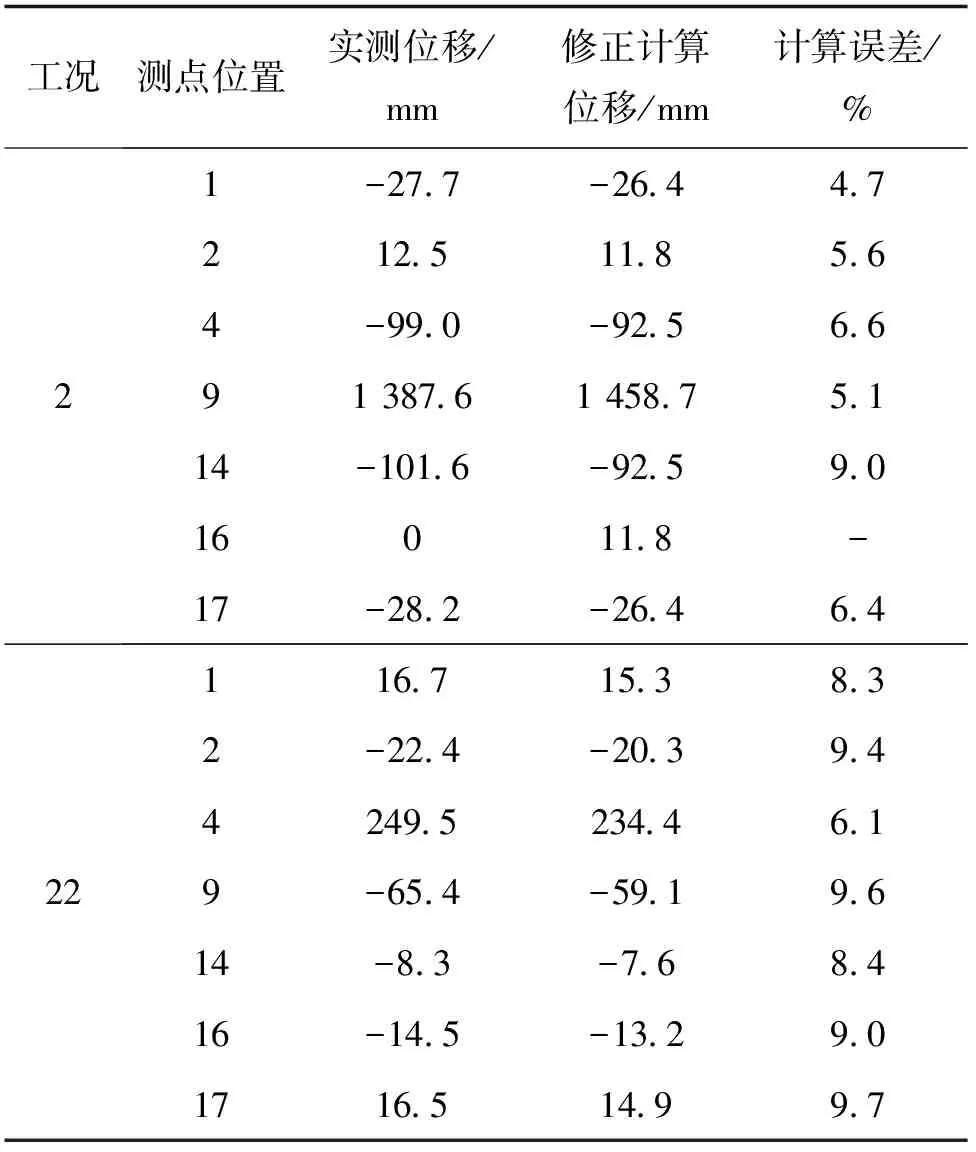
表5 模型修正15次优化前后工况2、工况22测点静力位移值对比

表6 模型修正优化前后修正参数值变化对比

由表5、表6可以看出,模型优化15次后位移误差降到10%以内,且主梁弹性模量变化量较斜拉索和主塔的弹性模量更大,证明主梁弹性模量在目标函数优化过程中作用较大、整体优化效果好。

4.2 动力频率模型修正优化

动力频率模型修正参数选择同静力位移目标函数修正参数,在软件中创建函数关系,给出约束条件后求解出各修正参数的增量,再进行后续分析计算。其中,不等式约束计算频率与实测频率的残差限值取5%,修正结果如图8、图9及表7所示。

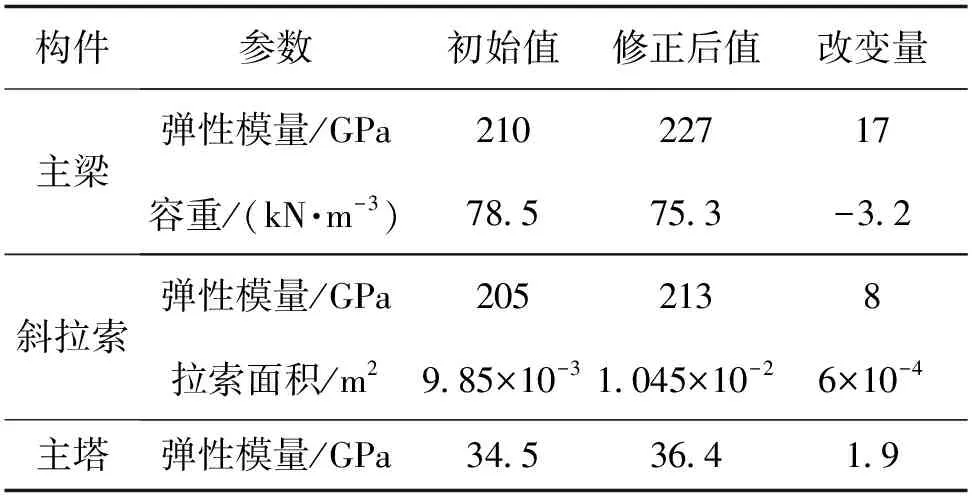
表7 模型修正前后修正参数值变化对比

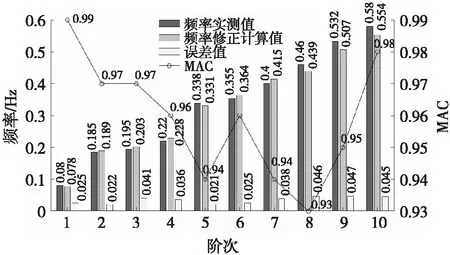
图8 模型修正7次优化前后动力频率特性对比

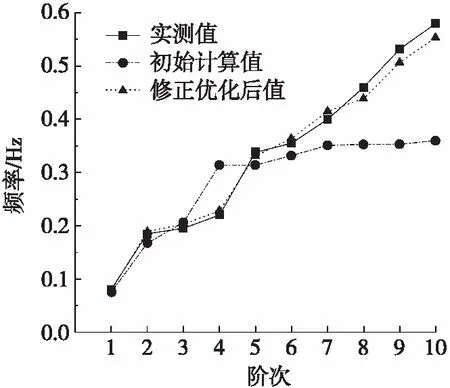
图9 模型修正优化前后各阶频率对比

结合图8、图9和表7分析可得,优化后的模型结构自振频率计算值误差小于允许误差,MAC值均超过90%,优化效果显著。

4.3 联合静动力模型修正优化

联合静动力模型修正优化同静力、动力模型优化过程大致相同,仅增添了分项权重系数的计算迭代,修正结果如表8、表9及图10所示。

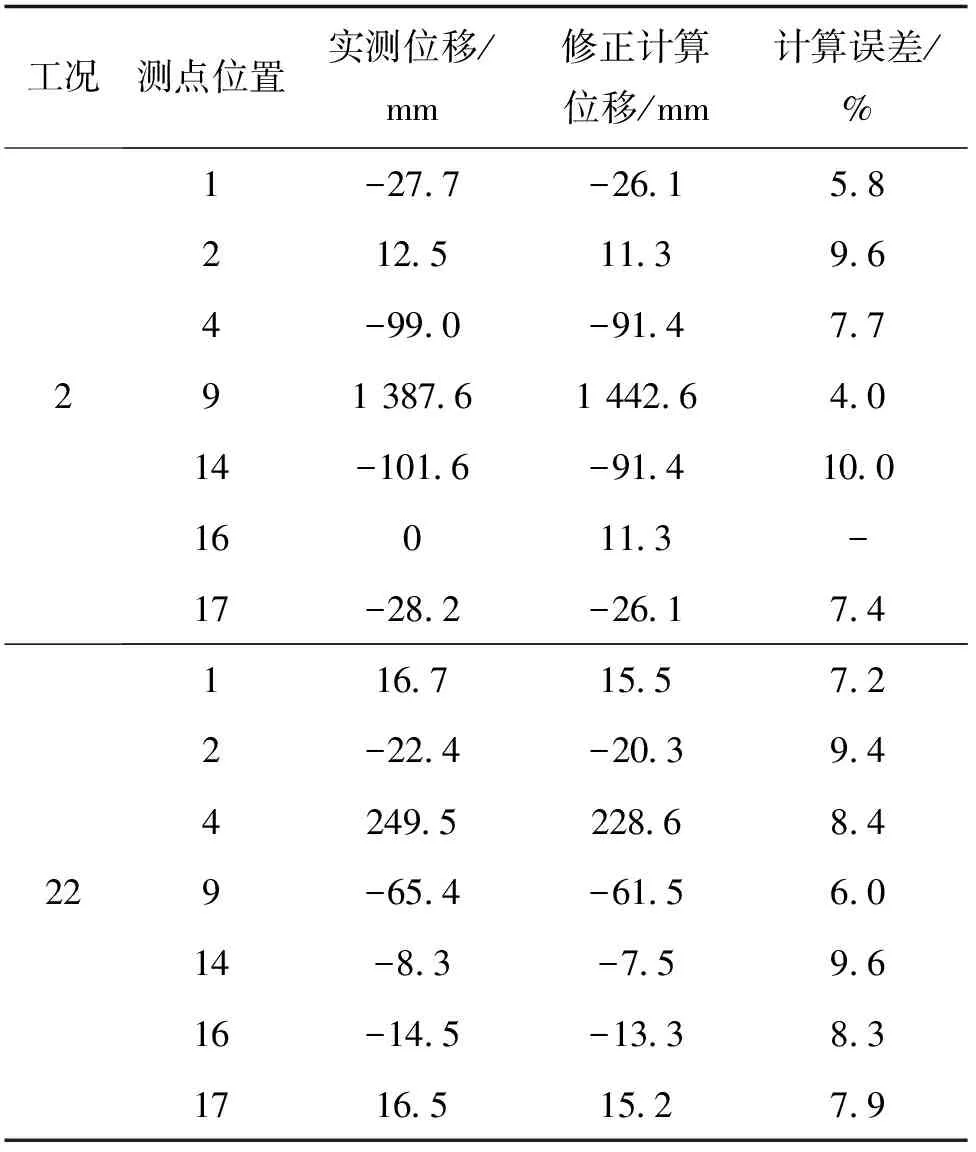
表8 模型修正优化前后工况2、工况22测点静力位移值对比

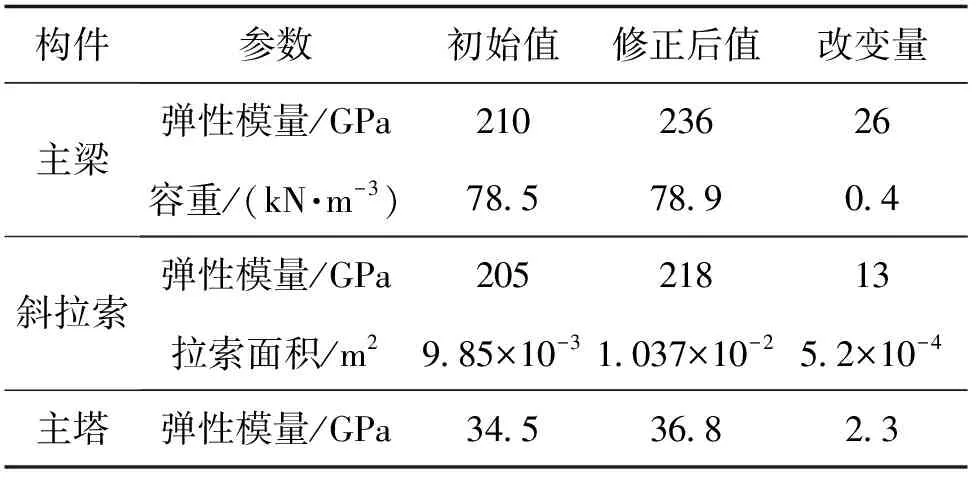
表9 模型修正前后修正参数值变化对比

图10 模型修正优化前后动力频率特性对比

对比表8、表9和图10可见,静力位移值误差、动力频率修正误差值均控制在允许误差以内,阵型匹配MAC值提升明显。

4.4 修正优化对比

将修正优化后模型的静动力响应特性与实际桥梁结构试验实测值进行了对比,结果如图11和表10所示。

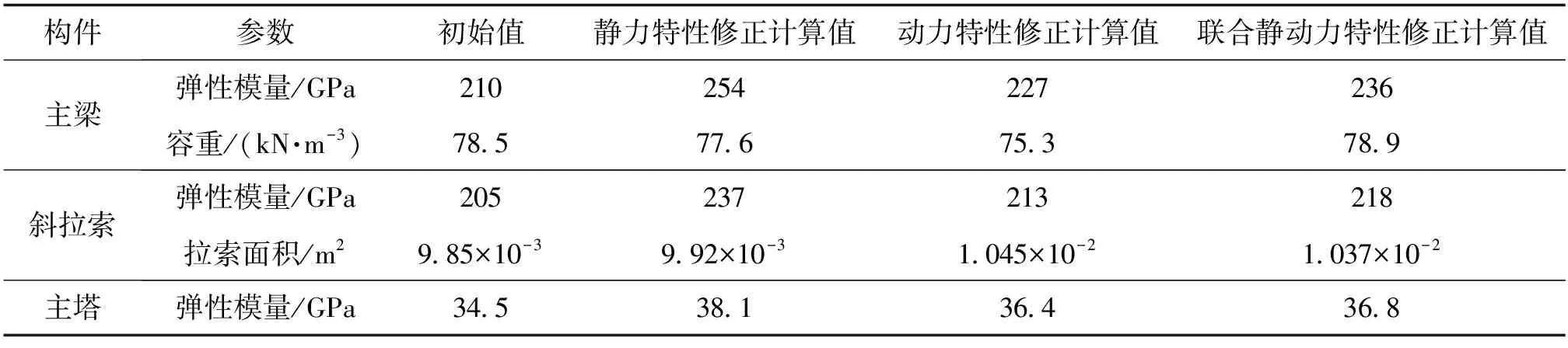
表10 静、动力特性与联合静动力特性修正后修正参数值对比

(a) 工况2静力与联合静动力特性修正位移值对比

综合图11和表10分析可见,各跨中点的静力位移值在联合静动力修正下的误差整体高于单静力修正的误差;联合静动力特性的修正后的模型结构自振频率更接近结构实际测量自振频率;主梁弹性模量在3种方法对应的结构响应中都起主导作用,印证了结构位移和频率参数灵敏度分析结果的一致性和准确性。联合静动力特性修正的参数变化更合理,且更符合结构各组成部分参数在桥梁结构建成后的变化。因此,联合静动力目标函数修正满足静、动力响应精度要求,且效率较高。

5 结论

桥梁有限元模型的精确程度影响桥梁结构运行的日常检修、损伤识别及安全评估,本文基于灵敏度分析和序列二次规划法对苏通长江大桥模型进行了修正优化,得出如下结论:

1) 结构位移对各修正参数灵敏度分析规律表明,结构材料弹性模量灵敏度:主梁>斜拉索>主塔;结构容重灵敏度:主梁>斜拉索>主塔容重,且斜拉索面积灵敏度又较主塔容重高。结构模态频率对结构各组成部分弹性模量灵敏度:主梁>斜拉索>主塔。

2) 静力位移、动力频率、联合静动力模型修正优化结果表明,静力位移、动力频率模型修正优化效果好,整体优化效果明显。联合静动力模型修正优化与原模型MAC值更匹配,目标函数修正效率较高。

3) 3种模型修正优化方法对比表明,主梁弹性模量在3种方法对应的结构响应中起主导作用。联合静动力模型修正的参数变化更符合实际监测数据,且更满足实际模型对静、动力响应特性精度要求。