高速涡轮泵多部件耦合转子系统动力行为

张国渊,廉佳汝,赵伟刚,梁茂檀,赵洋洋

(1.西安电子科技大学 机电工程学院,陕西 西安 710071;2.西安航天动力研究所,陕西 西安710100)

0 引言

液体火箭发动机高速涡轮泵低温推进技术是目前世界各航天大国深空探测运载器研发的核心技术,如美国NASA提出低温推进下的TOPS(Titan orbiter polar surveyor)深空探测器技术方案[1];法国航天局提出新一代的航天低温推进研究计划[2];日本在核心液体火箭发动机液氢液氧高速涡轮泵研究计划中强调低温下的轴承和密封技术研究[3];我国清洁低温燃料推进的长征5系列液体火箭研制中也采用液氧液氢低温介质为主介质[4]。低温介质下的发动机系统所处的复杂极端工况条件(如低温、低黏度、高速、高压、瞬态启动、大推力比、空间质量比限制等)也对发动机及其泵系统核心基础部件(如组合密封、支承轴承、轴向平衡装置等)的服役性能提升和可靠性增长提出了更严苛的要求[5]。组合密封定义为涡轮泵系统中的所有径向或轴向、静或动密封单元的集合,阻塞或防止被密封流体沿各类接触或摩擦副界面不可预期地泄漏。本文研究中将以多道浮环密封、轴端机械密封形成的组合密封、高速滚动轴承等构成的复杂多功能部件耦合的涡轮泵转子为对象,讨论其动力特性演变规律。对于多部件耦合复杂转子系统动力学特性演变的研究尚处在快速发展阶段;现有的研究仅限于单部件影响作用,如浮环密封、机械密封等的单独作用。

在浮环耦合转子系统特性研究方面,最早Kirk等[6]采用Ocvirk[7]定义的浮环动力学模型并将其引入分析转子系统特性,归纳了影响系统稳定性的因素,如浮环的交叉刚度、偏心率、供油压力和“有效长度”等。西安交通大学浮环密封研究小组在国内较早地开展了在系统稳定状态和失稳状态下浮环的理论和实验研究,指出浮环密封对转子特性有较大影响[8]。刘占生等构建了考虑温度、瞬态流体动压力和摩擦力等因素的密封—转子耦合动力学模型,分析了浮环引发轴系失稳的原因[9]。Xia等研究了浮环的质量、摩擦力、转子响应振幅以及浮环与转子之间的相互作用对转子系统动力特性的影响规律[10]。Liu等分析了干气密封浮环对系统动力特性的影响,并完成了密封的结构优化[11]。苏令等用微小位移和速度扰动法求解Reynolds方程获得了浅槽环瓣型浮动环的刚度和阻尼系数,并完成了系统稳定性分析[12]。近年来,杨宝锋等研究了浮环密封刚度阻尼系数对涡轮泵转子动力特性的影响规律,进一步表明密封对转子临界转速和响应均有较大的影响[13-14]。杜家磊等对某型涡轮泵动特性进行了仿真研究,结果表明流体密封附加刚度阻尼等对转子稳定性亦具有显著影响[15]。

在机械密封耦合转子系统特性研究方面,文献[16-17]将机械密封的刚度阻尼系数引入转子动力学方程,分析了系统的动力学行为;随后进一步考虑偏心产生的力和力矩耦合作用,开展了机械密封、转子和整机系统之间的运动学和动力学相关研究。近年来,Varney等利用弹塑性Jackson-Green粗糙表面接触模型对密封由于端面接触产生的效应进行量化分析,模拟了柔性安装定子(FMS)机械端面密封在非接触状态下的冲击现象,首次发现产生接触的某些参数会引起机械端面非周期振动;同时也提出了考虑密封间隙引起的各种力和力矩特性、转子动力学和惯性机动载荷影响的机械密封模型[18-19]。

在多部件对转子系统非稳态效应建模方面,研究者主要关注密封、轴承等组件受工况变化影响的静态阻塞效应和动态特性系数的变化规律。静态阻塞效应常用来解释微小间隙内流体的承载特性(即静特性),通过满足流体动压效应形成条件来实现;动特性系数用于表征部件动态行为特征,一般为刚度阻尼系数,其获得的常见方法为小扰动法求解全流体膜的雷诺方程。Hassini等发展了被密封低温介质气液两相转变过程中的属性效应对其动力学刚度阻尼系数的影响,同时分析了不同激振频率下系数的变化及系统动力学稳定性[20]。当考虑机械密封倾斜条件时,其动态系数可以含有更多的参数。文献[21-22]在机械密封瞬态过程的动力学分析过程中提出了瞬态动态系数的计算方法,得到了液/气态氧混合均质介质润滑模型下的密封动态刚度阻尼系数。但在启动阶段或者稳定运行阶段低温介质相变及混合润滑的接触状态下的密封动力性能演变机理尚无研究结果。

基于上述文献分析,已有的考虑多部件转子系统动特性研究主要倾向于获取各部件(如浮环密封、机械密封等)的动静特性,涉及组合密封、轴承等且耦合转子系统的完整动力学研究尚不足。同时,先进高速涡轮泵系统中,径向浮环与转子、轴向密封动环与静环组合密封—轴承—转子系统动力行为受极端工况(低温介质、微小约束间隙等)及时序运行规程(快速启停、高速运行等)影响的实际问题也越来越突出。基于此,本文将针对耦合多部件的高速涡轮泵转子进行瞬态启停和稳定运行等时序过程的动力行为特性研究,以此探讨其在全时序运行规程下的演化机理,结果可为相关工程应用提供参考。

1 理论模型

1.1 浮环密封动力系数求解模型

1.1.1 流体动压模型

图1为浮环密封工作状态结构图。

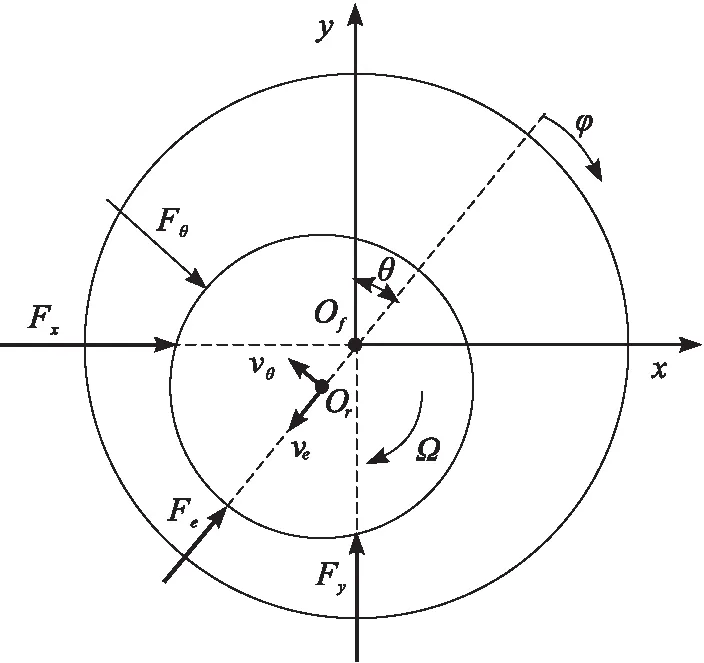
图1 浮环密封运动简图

随着转子系统转速的增加,当浮环重力、转子间的动压油膜力以及摩擦力之间达到平衡时,浮环锁死。浮环间隙流体动力控制方程为[23]

(1)

其中

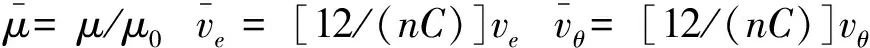
式中:φ为浮环密封的周向坐标;δ为液膜厚度;z为浮环密封的轴向坐标;ε=e/C为偏心率,e为偏心距,C为半径间隙;L为浮环密封宽度;n为转子转速;p为液膜压力;D为转子直径;μ为润滑介质的动力黏度,采用指数温黏模型μ=μ0e-α(T-T0),T0为起始温度,μ0为在温度T0下的润滑介质黏度,α为温黏指数。

1.1.2 动力学特性系数

浮环密封在轴系平稳运转状态下处于锁死状态,轴心在平衡位置附近做定常运动。因此,对流体压力积分获得油膜力,利用位移和速度扰动法可获得浮环密封在极坐标下的动特性系数,即

(2)

(3)

浮环的动特性系数在坐标系Of-xyz中表示为

(4)

(5)

1.1.3 边界条件

考虑供油压力pin的影响,则入口压力、入口温度、出口压力分别为

(6)

(7)

(8)

联立式(1)～式(8),采用有限元差分法进行数值求解,可得到浮环密封的动力学特性系数;具体的计算流程可见文献[24]。

1.2 机械密封力效应及耦合求解模型

1.2.1 动、静环间膜厚方程

图2为机械密封动、静环示意图。取静环表面为参考平面建立O-xyz坐标系,动、静环之间的液膜厚度为[25-26]

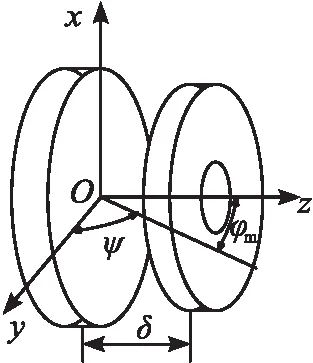
图2 机械密封动、静环示意图

δ=hm-ψrcosθm+φmrsinθm+hs

(9)

式中:hm为动、静环之间的初始间隙;ψ为机械密封动环轴心线与坐标轴z之间的夹角在y-z平面内的投影;φm为机械密封动环轴心线与坐标轴z之间的夹角在x-z平面内的投影;hs为螺旋槽槽深;θm为动环随转子的旋转角度。机械密封静环通常为平面,密封环动环表面开有深度为hd的螺旋槽,则在螺旋槽槽区有hs=hd,在非槽区有hs= 0。

1.2.2 流体动压模型

考虑挤压及动压效应下的无量纲流体动力控制方程为[27]

(10)

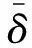
1.2.3 密封轴向力及力矩

机械密封平稳运转,对动、静环之间的介质压力p进行积分,得到动、静环之间动压力Frs和力矩Mrs分别为

(11)

结合图2定义的坐标系,将其分解到不同方向,有

(12)

(13)

机械密封动、静环之间的流体剪切力和剪切力矩[24]可表示为

(14)

(15)

(16)

式中v′为密封面间密封介质的流体速度。

由动压力产生的机械密封动、静环之间的摩擦力和摩擦力矩[19]可表示为

(17)

(18)

密封面间的摩擦因数μf在干摩擦下取0.26,在正常运行下取0.14[24]。

1.2.4 边界条件

机械密封的压力和速度边界条件主要为动环内径r1和外径r2上压力,即

(19)

式中:pin为机械密封腔的内压;pout为机械密封腔的外压,即环境压力。

机械密封的速度边界条件如下。

静环(z=0)速度为

vr=vθ=vz

(20)

动环(z=h)速度为

(21)

式中:vr为径向速度;vθ为半径为r处的切向速度;vz为动静环之间的挤压速度。

联立式(9)～式(21),采用有限差分法求解机械密封动静特性系数;在已有的研究基础上[22,24]开展具体求解过程的处理,实现了上述力、力矩及动特性系数的求解,具体计算流程和算例验证见文献[22,26]。

1.3 组合密封—轴承—转子系统模型

本文定义轴端点的位移为广义坐标,轴线方向为z轴,构建了包含多个组件如组合密封、轴承、转子等的系统动力学模型(见图3)。对任一节点自由度有5个,分别为x、y轴的平动和绕x、y、z轴的旋转自由度。模型中将系统按6个节点划分为5个单元,故总自由度数为30。其中节点1、节点5处为轴承单元,节点3处为浮环密封单元,节点6处为机械密封单元。

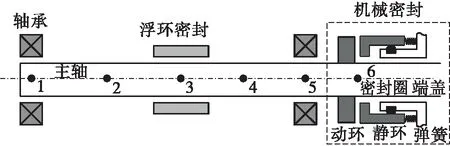
图3 组合密封—轴承—转子系统动力学模型

将机械密封动环模化为圆盘单元,推导出组合密封—轴承—转子系统的动力学微分方程[28],即

(22)

式中:M为系统的质量矩阵;Ω为转速;G为回转矩阵;C为阻尼矩阵,阻尼主要为浮环密封润滑介质阻尼;K为刚度矩阵;q为系统的广义坐标矩阵,q= {xi,yi,θxi,θyi,ψi},对应的自由度如图4所示;下标i(i=1,2,…,6)表示第i个节点;Fd和Md分别为油膜作用施加在动环上的力和力矩,包括动环的重力Fgr,流体动压力Fr和动压力矩Mr,流体剪切力Fμr和剪切力矩Mμr,以及摩擦力Ffr和摩擦力矩Mfr。

图4 弹性轴段自由度

本文在已有研究基础上完成了对动力学模型的求解,采用的动力学分析方法与算例验证见文献[28-29]。

1.4 系统稳定性分析

干扰系统稳定性的因素有冲击、密封力、转子不平衡力、轴承力、油膜涡动等。本文依据API617中规定用对数衰减率δ′来评估转子系统的稳定性[30]。对数衰减率定义为

(23)

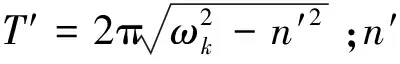
综上,为了得到组合密封—轴承—转子系统模型的密封行为和动力学行为,首先需分别确定浮环密封和机械密封的动力学性能,随后再利用有限元方法建立系统运动方程,将浮环和机械密封的动静特性参数引入矩阵中求解。具体求解计算流程如图5所示。

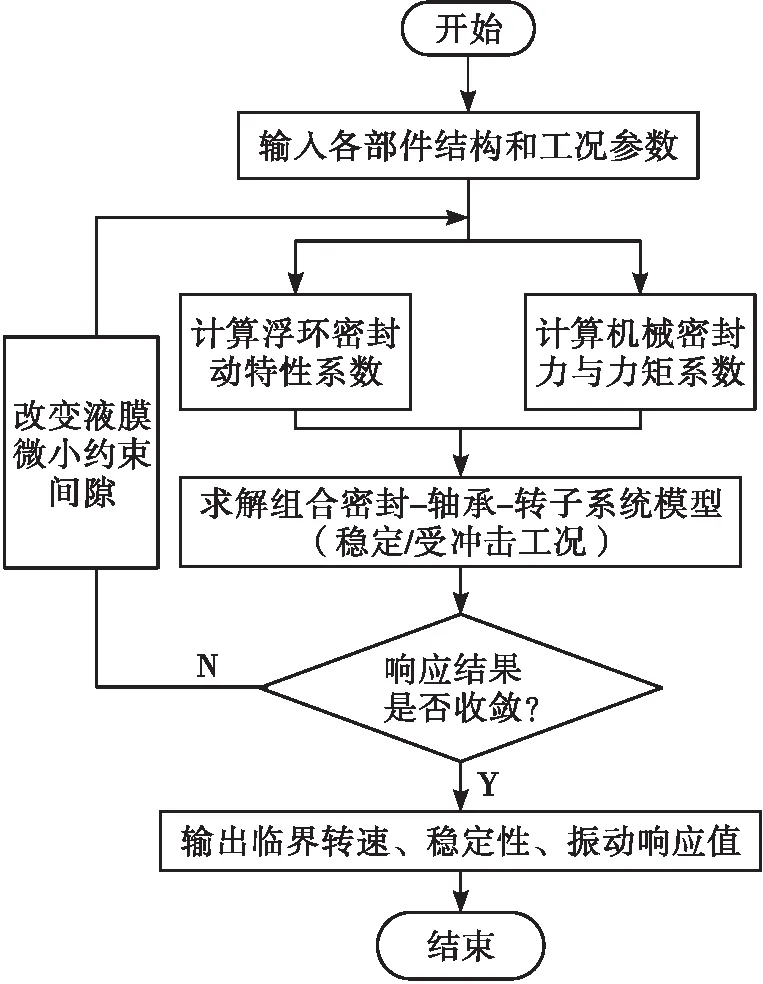
图5 组合密封—轴承—转子系统特性计算流程图

由图5可知,本文所采用的方法耦合了多个部件的动力系数,代入动力学模型完成具体计算;对比直接引入浮环密封力、机械密封力与力矩等结果作为计算条件,是一种较为简便且精度较高的方法,能有效避免计算耗时较长及在计算过程中由于可能出现的大量局部循环造成难以收敛的情况。

2 算例验证

本文采用刘占生[9]、Childs的实验[31]和理论[32]中的算例对提出的模型和计算方法进行验证。算例中浮环密封的结构参数和工况条件参见文献[9,32]。浮环刚度和阻尼随偏心率变化如图6和图7所示。

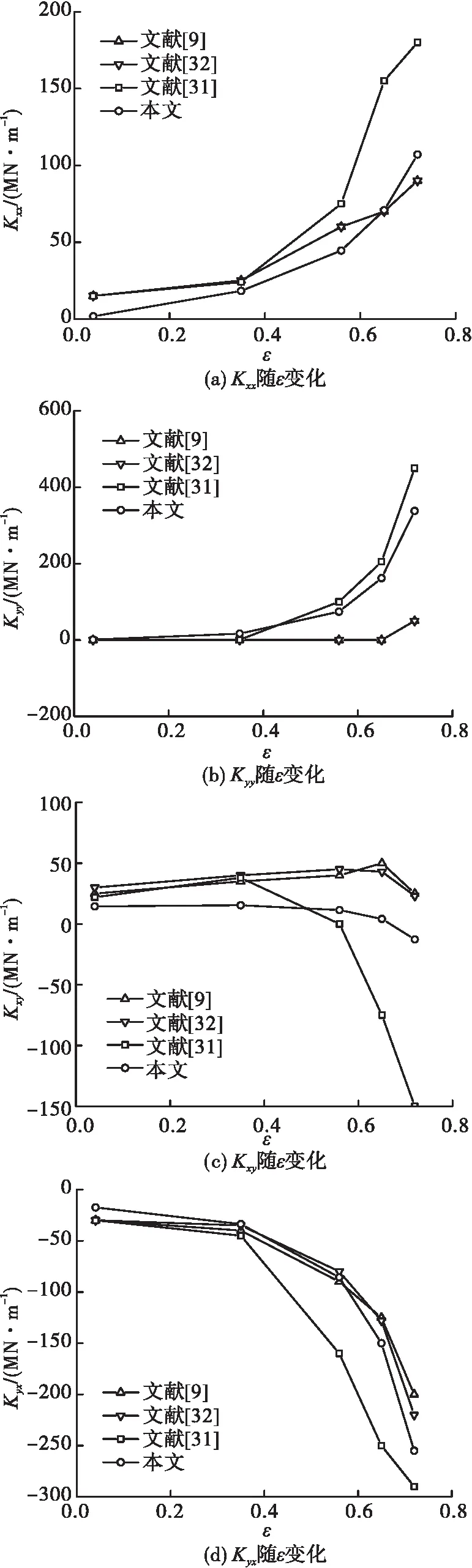
图6 浮环刚度随偏心率的变化

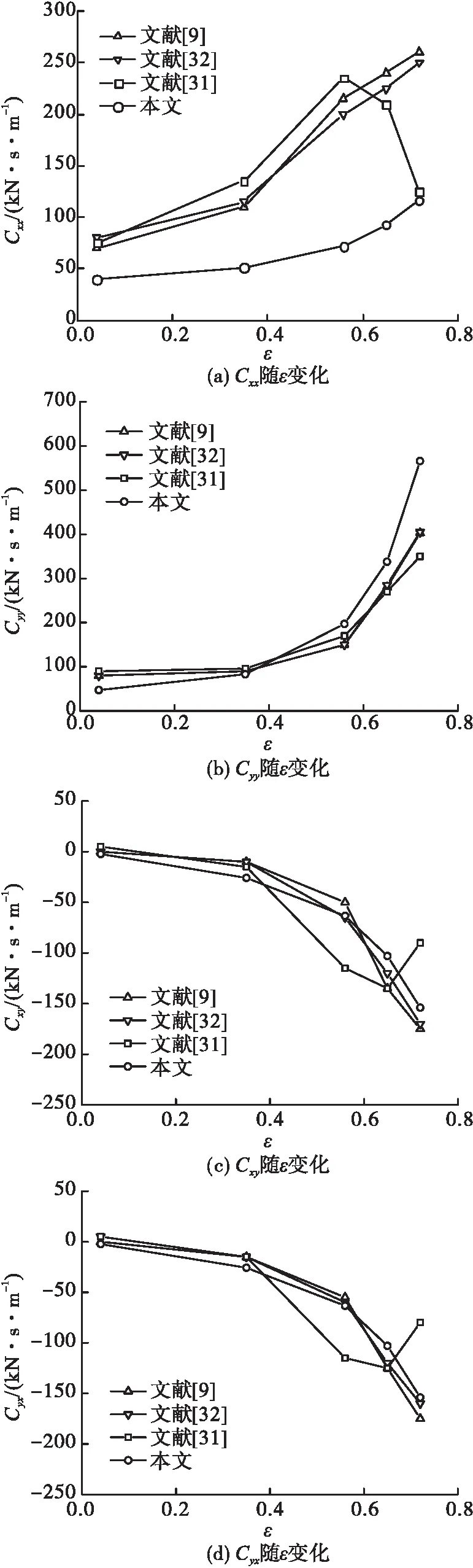
图7 浮环阻尼随偏心率的变化

由图6可见,主刚度Kxx和Kyy随偏心率ε的变化趋势与文献一致。Kxx计算结果与文献的偏差在偏心率ε = 0.04时达到最大,偏心率ε = 0.65时达到最小,仅为1.2%。Kyy与文献实验结果吻合良好。交叉刚度Kxy和Kyx随偏心率ε的变化趋势均与文献理论结果基本保持一致。Kyx主要体现为负刚度,随偏心率ε增大而持续减小。负刚度Kyx远大于主刚度Kxx和Kyy,严重影响了轴系稳定性。

由图7可见,主阻尼Cxx和Cyy随偏心率ε的增加均保持上升趋势,与文献理论结果一致。Cxx与文献的偏差在偏心率ε <0.75时较大,偏心率ε = 0.75时,其与实验值非常接近,偏差仅为7.43%。Cyy随着偏心率ε的增大而逐渐增大,与文献结果保持了很好的一致性。Cxy与Cyx数值上相等,Cxy与Cyx均随偏心率ε的增加而逐渐减小,当偏心率ε>0.56时出现了较大的偏差,可能产生了两相流现象。

基于上述分析,浮环动特性系数在各偏心率ε下,计算结果与文献保持了很好的一致性,其平均偏差保持在15%以内,主刚度Kyy和主阻尼Cyy与文献实验结果很好地吻合。对比结果表明本文关于浮环密封动特性系数的建模和计算方法是可行的。

3 计算实例

3.1 浮环密封的动特性系数计算

某高速涡轮泵工作中处于低温液氮环境,表1中给出了浮环的结构和工况参数,刚度阻尼系数随偏心率的变化如图8所示。

表1 浮环密封的结构参数和工况条件

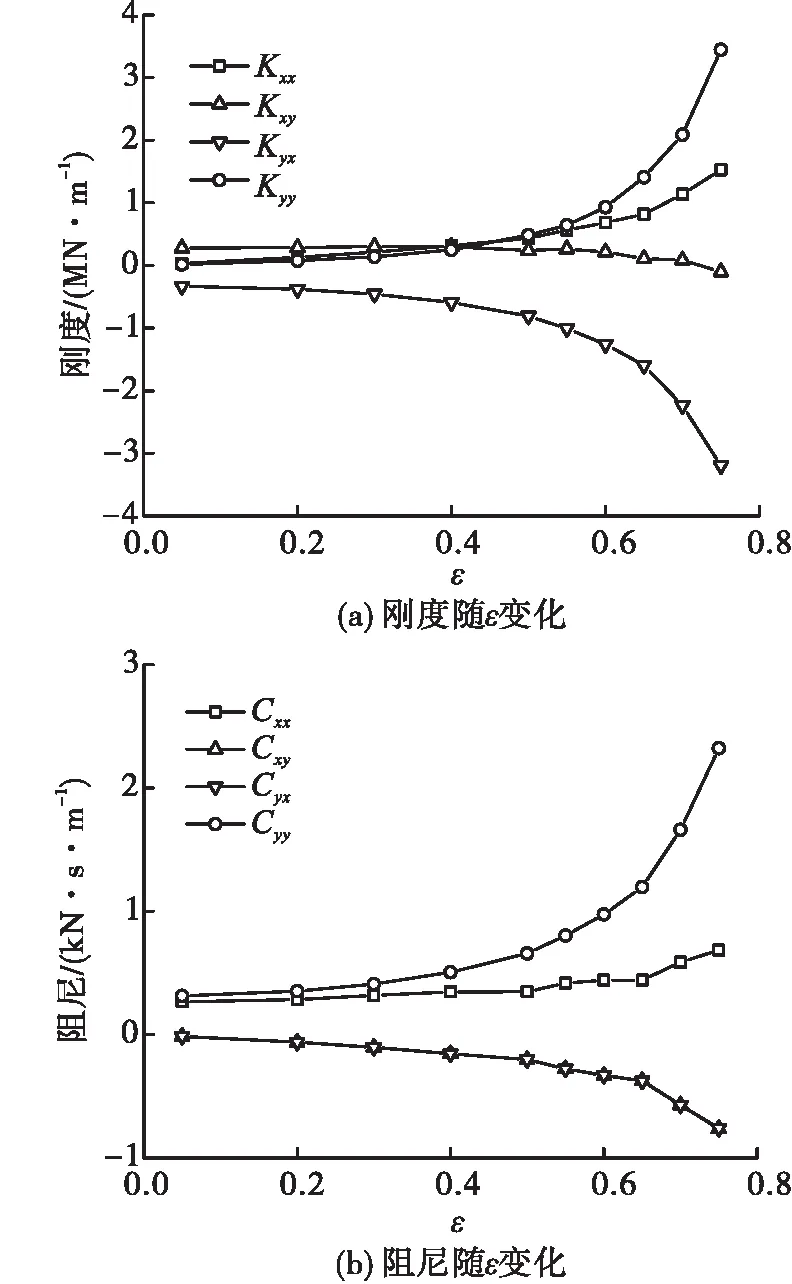
图8 浮环刚度和阻尼随偏心率的变化

由图8 (a)可见,主刚度Kxx和Kyy随ε的增大而增大。交叉刚度Kxy和Kyx随着ε的增大而减小,在0.65<ε<0.7之间,Kxy跨越0刻线成为负刚度;Kyx恒为负,极大地降低了轴系的稳定性。由图8(b)可见,主阻尼Cxx和Cyy随偏心率ε的变化关系与主刚度Kxx和Kyy类似,浮环的交叉阻尼Cxy和Cyx恒为负值,是系统不稳定的因素。

3.2 机械密封的力及力矩计算

某涡轮泵用螺旋槽机械密封的端面结构如图9所示。

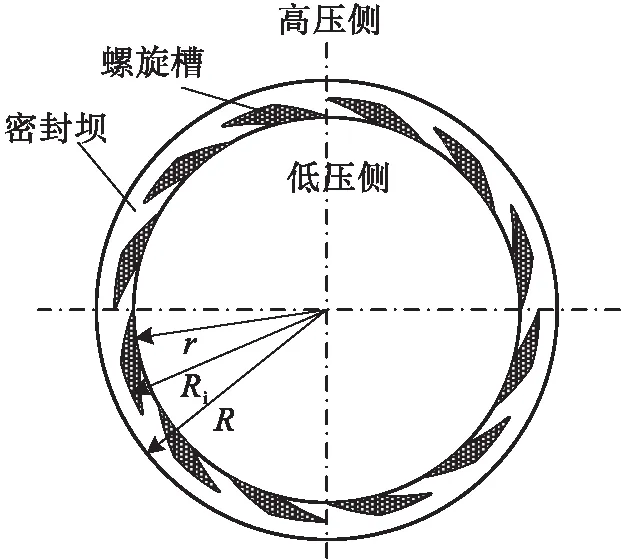
图9 螺旋槽机械密封结构图

高压侧与低压侧之间由密封坝隔开,内外表面由螺旋槽和密封坝组成,黑色区域为密封槽,静环表面光滑无槽型结构。机械密封动环端面的结构参数和工况条件如表2所示。密封外径压力1 MPa,内径压力0.1 MPa。

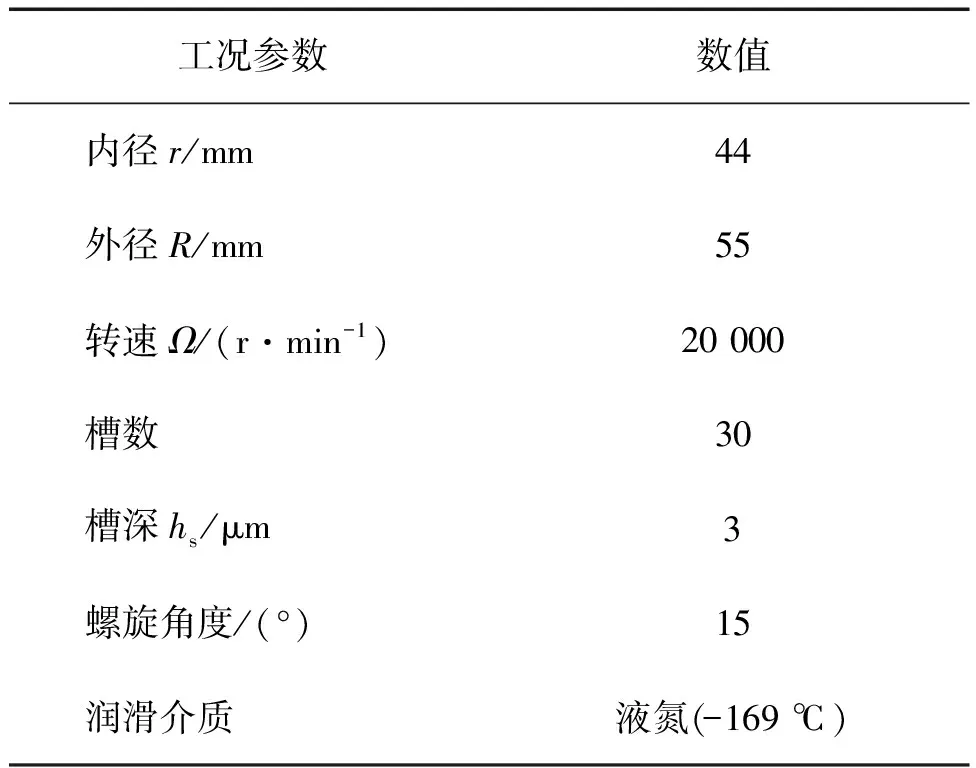
表2 机械密封结构和工况参数

在实际工况下,机械密封动、静环之间存在不对中情况,ψ和φ随时间t的变化关系可用周期性简谐运动方程来表示,即

(24)

式中:A和B分别为倾角ψ和φ的最大取值,考虑加工、装配等工况条件均取为2°;ω为动环随轴系的涡动频率(转频);θA和θB为机械密封的初始相位角,取为0°。

密封动、静环之间的动压力Frs和力矩Mrs随密封间隙Cm和轴系转速Ω的变化而变化,当轴系转速在工作转速20 000 r/min时,动压力Frs和力矩Mrs随密封间隙Cm的变化如图10所示。当间隙Cm为3 μm(与槽深一致)时,动压力Frs和力矩Mrs随转速Ω的变化如图11所示。

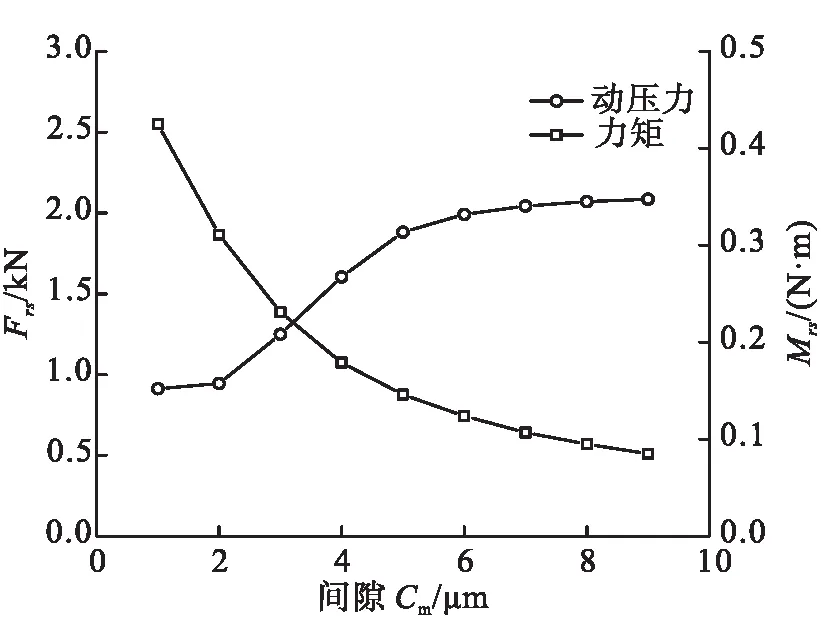
图10 动压力Frs和力矩Mrs随密封间隙Cm的变化

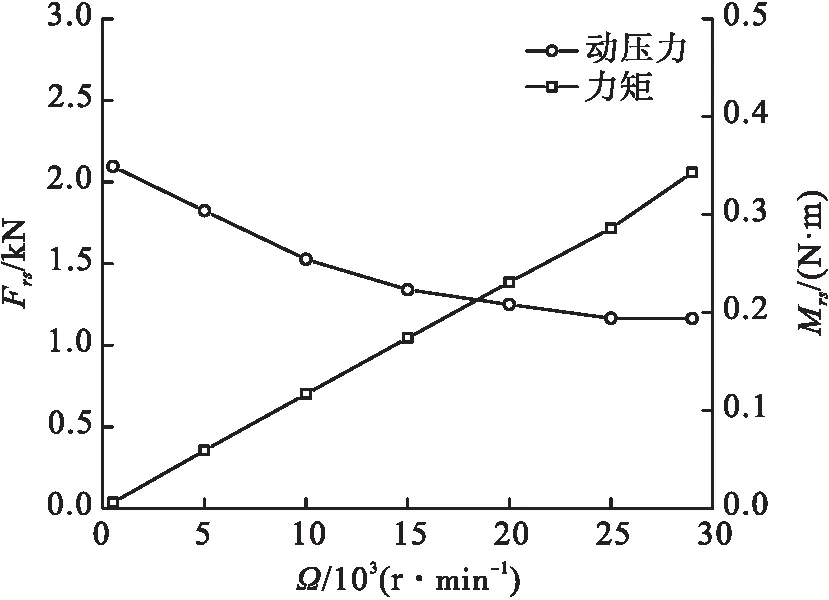
图11 动压力Frs和力矩Mrs随轴径转速Ω的变化

由图10可见,随着间隙Cm的增大,动压力Frs由一恒定值持续增大到另一恒定值,表现出在低黏度介质下动、静环之间静压力和动压力的变化规律。动压力矩Mrs随着间隙Cm的增大而持续减小。由图11可见,随着轴系转速Ω的增大,动压力Frs随转速Ω逐渐减小,力矩Mrs线性增大。

利用式(12)和式(13)将动压力Frs和力矩Mrs分解,在工作中转速20 000 r/min、间隙3 μm下,获得力Fx、Fy和力矩Mx、My、Mz随时间t的变化曲线如图12和图13所示。

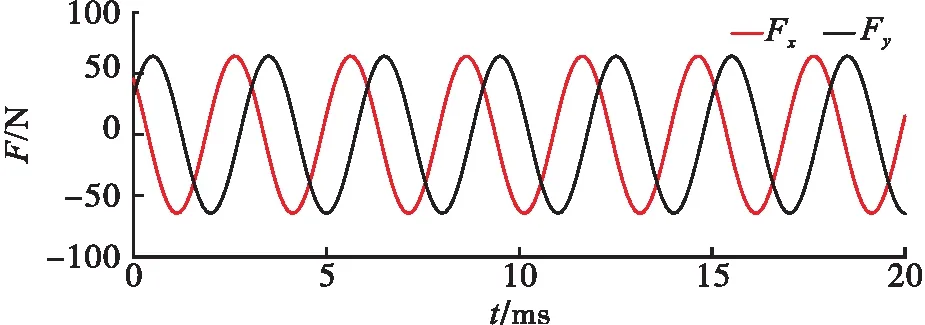
图12 Fx和Fy随时间t的变化

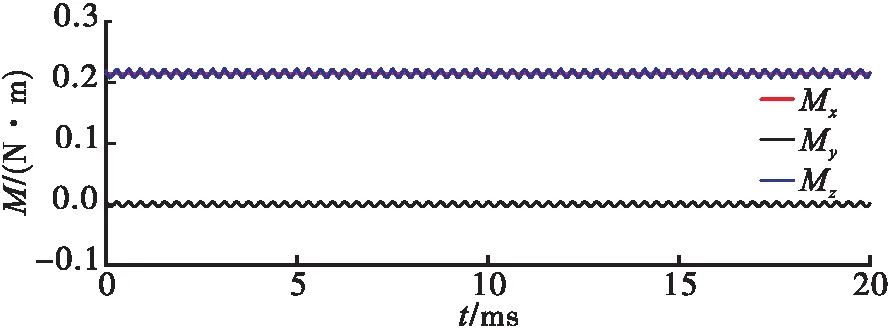
图13 Mx、My、Mz随时间t的变化

由图12和图13可知,力Fx和Fy随时间的变化波动明显;力矩Mx、My和Mz较小,随时间的变化无明显波动,My的值趋近于0,可忽略不计。

3.3 组合密封—轴承—转子系统动力学分析

对浮环密封、盘单元、轴承和机械密封等模化,某涡轮泵转子模化后的节点划分如图14所示。由图14可见,转子系统包括盘(集中质量,节点4、13、18),轴承(位于节点8、9),密封(浮环密封位于节点10、11、15,机械密封位于轴端节点24)以及轴段,轴系材料及轴承刚度系数等如表3所示。

表3 主要结构参数

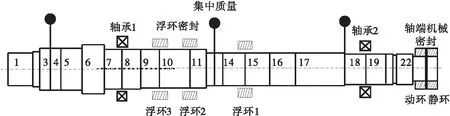
图14 组合密封—轴承—转子系统模化模型

为讨论多部件耦合因素对转子系统动力行为影响,分别从不考虑密封部件耦合、不同浮环密封数量、浮环与机械密封组合等多种不同形式密封与轴承—转子系统动力特性角度,表4给出了计算过程中定义的5类密封—轴承—转子系统计算说明。

表4 定义的转子系统组成类型及计算说明

3.3.1 组合密封对系统弯曲临界转速的影响

根据表4中转子类型,通过数值计算获得不同转子系统类型下系统的临界特性如图15所示。

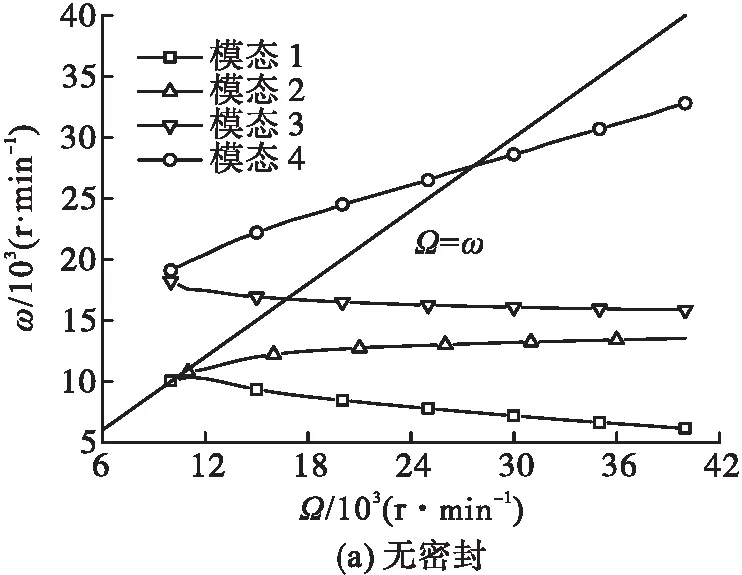
图15 不同组合密封系统涡动频率

整理上述计算结果,组合密封对系统临界转速的影响特性如图16所示。由图16可见,浮环的添加对转子系统的前四阶临界产生了一定的影响,表现为先增大后减小的趋势,其中二阶临界变化最为明显。此外,机械密封不影响系统的临界特性和稳定性。

图16 各类型转子系统临界转速

3.3.2 组合密封对转子系统稳定性的影响

根据表4中转子类型,通过数值计算获得不同转子系统类型下系统的稳定性,如图17所示。

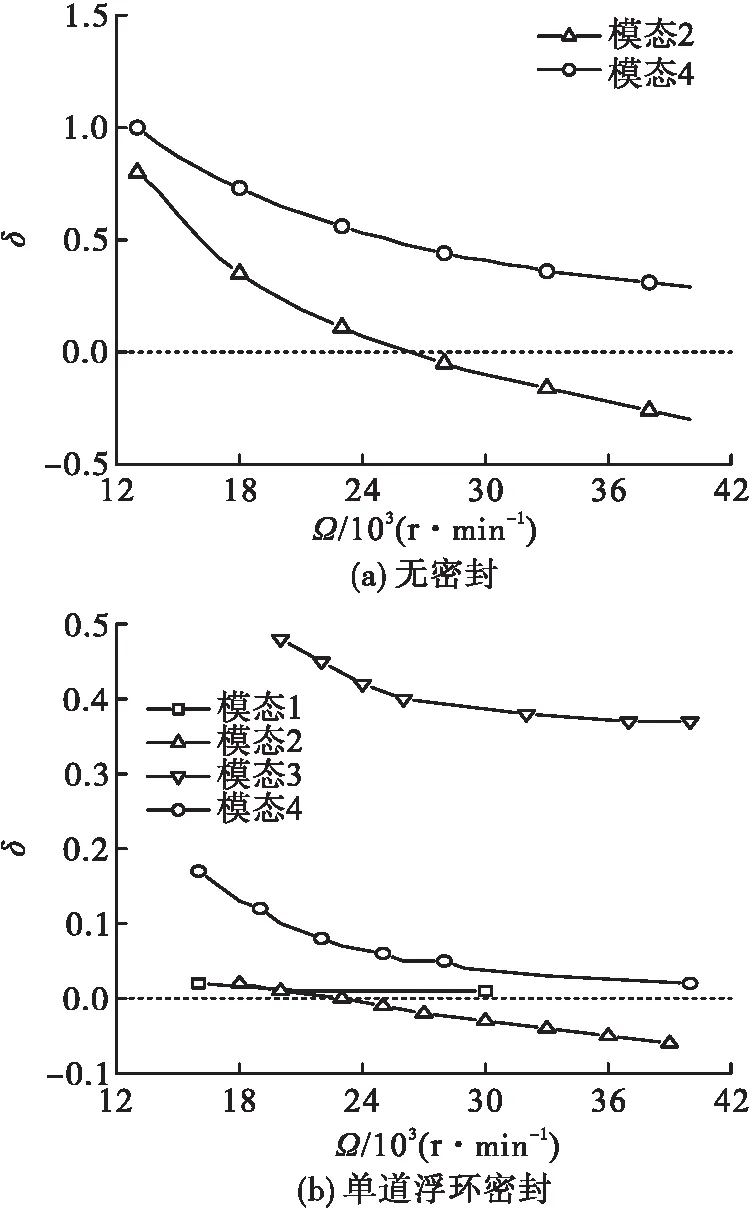
图17 不同组合密封系统对数衰减率

整理数据,可得不同组合密封对转子系统稳定性的影响规律,如图18所示。从图18可见转子系统易发生二阶模态失稳,失稳转速随浮环的添加发生了明显的变化,整体趋势是减小的;机械密封对系统失稳转速的影响较小。

图18 各类型转子系统失稳转速

3.3.3 组合密封对转子系统瞬态响应的影响

系统的弯曲特性受机械密封静特性的影响尤为突出,如图14所示的转子系统,当涡轮泵在瞬态启动过程中,机械密封会经历一个从端面接触到非接触的脱开状态(本文中以启动后0.8 s时密封端面脱开为例),特模拟机械密封受动压作用而脱开,脱开过程中由于密封间隙的增加会导致瞬间动静环不对中,进而产生瞬态动压力和动压力矩作用(以瞬态简谐力模拟力及力矩作用),在工作转速下(20 000 r/min)转子系统轴承1(节点8)、浮环密封1(节点15)和轴承2(节点19)处瞬态响应如图19～图21所示。

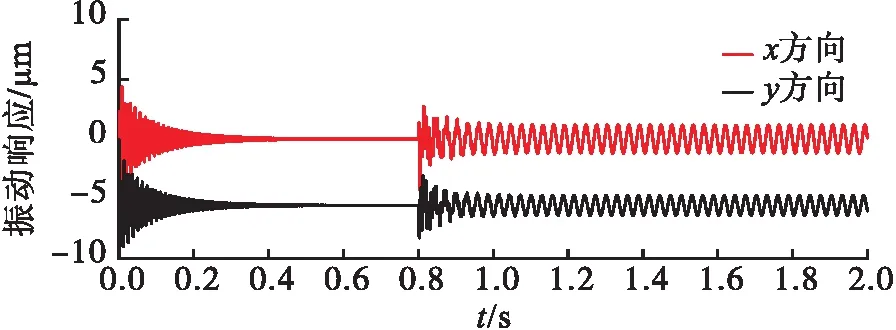
图19 轴承1处位移响应

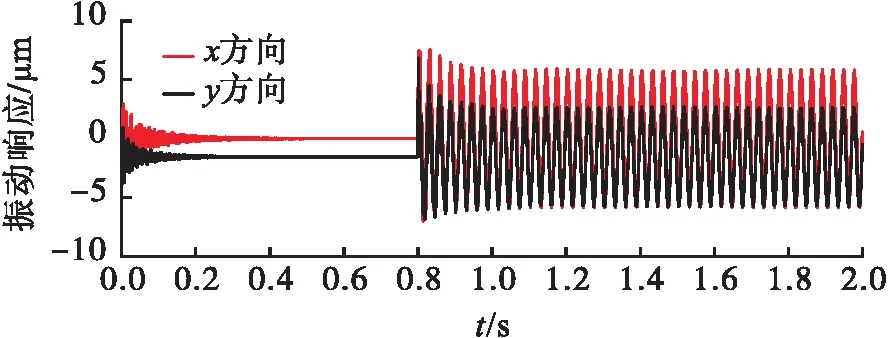
图20 浮环密封1处位移响应

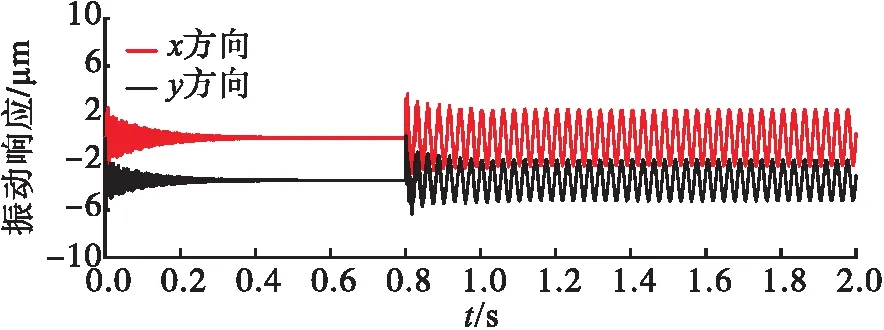
图21 轴承2处位移响应

由图19～图21可见,随着涡轮泵启动经过0.8 s后,端面机械密封脱开,形成非接触机械密封,其给转子系统造成的冲击激励会影响随后0.2 s的振动响应,但系统在工作转速下能很快地再次达到稳定运转状态。该过程中,轴承处的振动响应在y方向因重力作用偏离位移0刻度,平衡位置处于y轴负半轴。浮环密封位置处的振动响应值明显大于轴承处,且增加较为显著,这可能会对密封性能带来一定的影响,即可能会导致不期望的密封泄漏量的出现,需要在后续研究中予以充分关注。

4 结论

开展了对多部件耦合高速涡轮泵转子系统动力学特性的研究,得到以下结论。

1)推导了浮环密封和机械密封的刚度阻尼系数求解模型,给出了因机械密封动、静环不对中引起的流体动压力和动压力矩、摩擦力和摩擦力矩、剪力和剪力矩等的求解方法,构建了考虑浮环、机械密封等多部件耦合的组合密封—轴承—转子系统动力学分析模型,求解模型可获取系统的涡动速度、失稳转速、对数衰减率以及瞬态响应等。

2)对比已有文献,本文所构建求解模型获得的浮环特性与文献试验和理论结果高度一致,平均误差在15%以内,表明本文浮环密封模型与求解方法的正确性。

3)数值仿真结果表明多道浮环密封改变了系统的临界特性和稳定性特征,而机械密封并无此特征;机械密封不对中特性导致系统的瞬态响应升高。

4)高速涡轮泵启动过程存在的机械密封瞬态脱开现象,其对转子系统会产生瞬时冲击,但系统能在较短的时间内再次达到稳定运转状态;机械密封脱开后,随着转速增加,系统的动力响应明显增加。高速稳定运转过程多道浮环密封对系统稳定性呈现出降低失稳转速的不利影响;振动响应会对浮环密封的间隙产生影响,进而影响其密封性。