基于MWorks的自动器-管路系统动态特性仿真

孙永鑫,周晨初,张黎辉,胡海峰

(1.北京航空航天大学 宇航学院,北京 100191;2.西安航天动力研究所 液体火箭发动机技术重点实验室,陕西 西安 710100)

0 引言

自动器是液体火箭发动机系统中的重要组成部分,用于调控发动机的工作过程,维持系统的稳定性和可靠性。流量调节器、单向阀是典型的自动器组件,流量调节器通常安装在推进剂供应管路中,用于满足工作过程中燃料流量稳定和调节的要求,其静、动态性能的优劣直接影响发动机的工作性能[1];而单向阀位于发动机蒸发器流路上,防止在预冷过程中低温推进剂进入蒸发器,直接关系到发动机能否正常工作。某型液氧煤油发动机在一次试车过程中,低温液氧单向阀发生自激振荡且频率接近预燃室一阶纵向声学固有频率,引起系统内出现强烈的振荡响应,对发动机工作的可靠性造成严重的威胁。因此,有必要对流量调节器、单向阀的流路系统开展动态特性研究。

对于自动器系统,研究表明其稳定性通常与所在的供应系统相关。Rivera对气动系统的两级电动气阀及前后管路建立集中参数模型,通过数值积分法探索了系统在不同工作条件下的非线性不稳定,得到了系统的稳定域,并研究了阀孔直径等结构参数对系统稳定域的影响[2]。Hayashi等研究了由一根短管与贮箱连接的提升阀组成的系统,分析了阀芯小开度下的不稳定性,得到了系统不稳定区域,并探索了不同初始条件对不稳定区域的影响,同时识别出两种类型的自激振荡[3]。Misra针对包含控制阀和供应管路系统的自激振荡问题,通过仿真揭示流体与结构的相互作用是自激振荡的原因,并详细分析了引发自激振荡的过程[4]。

从国内外研究来看,自动器管路系统在时域上的表现特征为系统状态变量随时间的变化,可以反映出系统出现自激振荡时的特征、系统稳定域及固有频率下状态参数的振荡特性等;而在频域上的表现特征为对特定扰动的状态变量响应随扰动频率的变化,可以反映出局部振荡对系统参数的影响规律以及系统不同组件间的耦合稳定性等。

在液体火箭发动机系统动态特性研究中,多数研究者采用传统的AMESim、MATLAB系统仿真软件[5-12]。传统系统仿真软件建立的发动机系统结构复杂,通用性较差,难以满足多型号发动机系统动态特性研究。针对上述问题,本文采用国产自主化系统仿真软件MWorks建立通用性较强的组件模型,开展自动器管路系统动态特性仿真。

MWorks是由苏州同元软控开发的系统仿真软件,这一软件基于多领域统一建模规范Modelica,可以提供系统仿真中所需的仿真建模、编译分析、仿真求解和后处理等过程[13]。软件所建立的Modelica模型采用微分、代数和离散方程组来进行数学描述,具有如下特点:①面向对象建模;②多领域统一建模;③基于非因果建模;④连续离散建模[14-15]。基于这些特点,MWorks平台可以实现模型重用、重构和扩展,极大降低了系统仿真的难度。

1 数学模型及仿真方法

1.1 数学模型

1.1.1 流量调节器—管路系统模型

本文研究的流量调节器的主要结构如图1所示,包括两级节流机构,第一级节流机构由齿条组件、节流口构成,通过齿条组件控制节流口的开度,从而改变输出的稳态流量;第二级节流机构由滑阀、弹簧、阻尼孔、滑阀口构成,通过弹簧弹力和液体作用力控制滑阀位移,维持节流口前后压差恒定,从而保证输出流量的稳定[16]。

图1 流量调节器示意图

流量调节器模型采用了文献[17]中描述其动态过程的数学模型,由于调节器传递矩阵计算过程涉及五阶矩阵运算,矩阵形式过于复杂难以在MWorks平台上输入和运算,考虑到MWorks平台支持陈述式非因果建模,可以采用陈述式方程来表达模型,因此直接对文献[17]中的式(6)～式(10)进行拉普拉斯变换,得到以拉普拉斯算子s为变量的频域模型,即

(1)

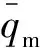
流量调节器的主要参数如表1所示。

表1 流量调节器主要参数

流量调节器—管路系统的基本结构如图2所示,由恒压源、液体管路和流量调节器组成,调节器后压力恒定,管路入口存在一定的局部阻力,其中流体管路模型采用文献[17]中的无损管路模型。

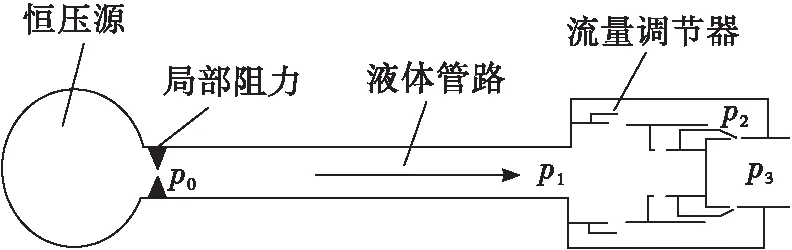
图2 流量调节器—管路系统示意图

1.1.2 单向—管路系统模型

本文研究的单向阀主要结构如图3所示,由阀芯、壳体、弹簧等组成。当阀芯前后压差作用力不足以克服弹簧弹力时,阀芯与阀座左端闭合来阻止液体通过;当阀芯前后压差作用力逐步增大到完全克服弹簧弹力时,阀芯会向右侧移动直至阀座右端,液体通过环形节流口和阀芯小孔流过单向阀[18]。

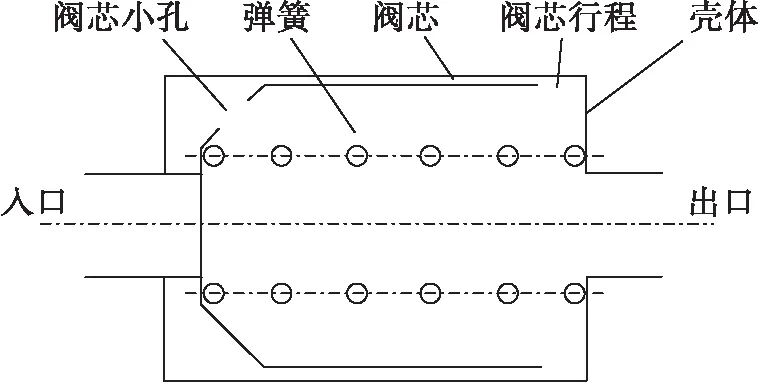
图3 单向阀示意图

单向阀模型采用了文献[19]中描述其动态过程的方程作为其时域模型,表达式为

(2)

式中:x、v、m分别为阀芯开度、速度、折算质量;qmx为流过单向阀阀芯的质量流量;p1、p2、p3分别为单向阀入口、中间腔、出口压力;A1、A3分别为入口压力、出口压力的作用面积;f为阀芯导向面间隙黏性摩擦力系数;Ff、Fs、Fi分别为干摩擦力、稳态液动力、瞬态液动力;Jv为单向阀内流体的惯性系数;ζx、ζh分别为节流口、阀芯小孔的流阻系数。单向阀主要参数如表2所示。

表2 单向阀主要参数

单向阀—管路系统的基本结构如图4所示,由液体管路、节流圈和单向阀组成。共有4段液体管路,均采用文献[19]中的分段集中参数动力学模型,且系统进出口压力为定值。

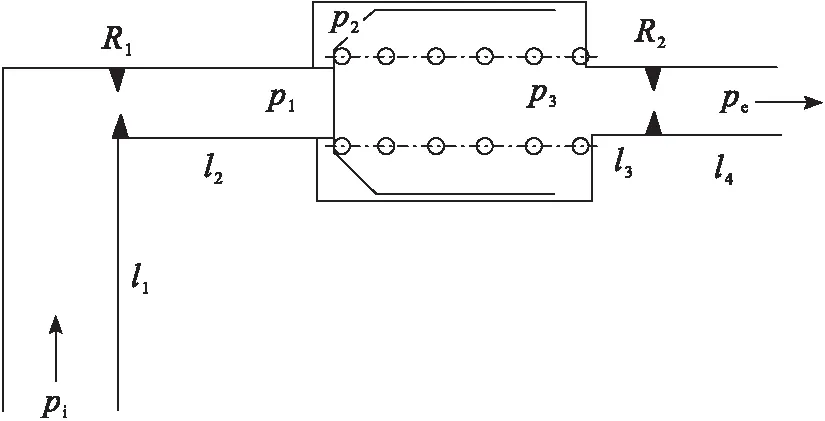
图4 单向阀—管路系统示意图

1.2 仿真方法

Modelica是一个开放的面向对象的物理系统多领域统一建模规范,以微分方程、代数方程和离散方程为数学表示形式。在先前多种建模语言的基础上,Modelica继承了优秀特性,从原理上统一了之前的各种多领域统一建模机制,直接支持基于框图建模、基于函数建模、面向对象和面向组件建模,通过基于端口与连接的广义基尔霍夫网络机制支持多领域统一建模。

由于MWorks以时间为仿真变量,而频域特性是传递函数的相关量随频率的变化特性,因此需要建立频率与时间的关系。研究中考虑到多数组件频域模型中的传递矩阵均含有拉氏算子s,因此采用了Modelica规范中的inner/outer关系,将拉氏算子s设定为全局变量。根据拉氏算子s与频率f间的关系(s=j2πf),将频率f设置为仿真时间t的函数f(t)。通过调整仿真时间来控制频率范围,采用Modelica标准库中的复数计算函数,根据频域特性参数的定义式得到所求量(幅值、相位等)随频率f的变化曲线。

在MWorks中基于Modelica建立模型并仿真的流程如图5所示。

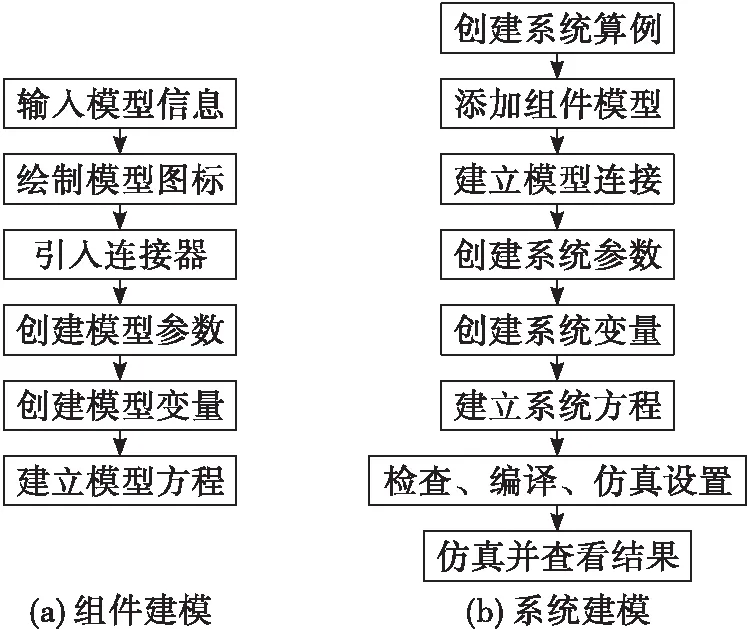
图5 MWorks建模流程图

其中组件建模过程如下。

1)输入模型信息:包括模型名、类别、描述、存储位置等,较为常用的类别包括模型model、端口connector和命名空间package,分别用于定义组件模型、组件间连接的连接器和模型库的目录层次。

2)绘制模型图标:在模型的图标部分绘制,为组件的图形显示。

3)引入连接器:为了实现不同组件间的连接和状态变量的传递,组件模型中通常会引入连接器模型,连接器模型通常需要传递压力和质量流量。

4)创建模型参数:在模型的文本部分创建,需在创建的参数前加入关键词parameter,作为与模型变量的区别,由于组件频域数学模型中的参数存在单位且涉及复数计算,所以需要在创建参数前引入Modelica标准库中的国际单位库、虚数单位j和复数运算库。

5)创建模型变量:在模型的文本部分创建,包括数学模型中的状态变量、中间变量等,以及全局变量拉氏算子s。

6)建立模型方程:需在关键词equation后建立模型方程,包括组件输入输出状态变量与连接器变量传递方程、中间变量计算方程及其他计算式等,最终建立Modelica程序。

系统建模过程如下。

1)创建系统算例:该过程与创建组件模型中的过程1)基本一致。

2)添加组件模型:当系统模型的图形部分完成时,在模型浏览器中将所需的模型拖拽到模型的图形视图中,即可在系统模型中添加组件模型。

3)建立模型连接:根据对实际发动机系统的模块化划分结果,将相邻组件的连接器进行连接。

4)创建系统参数:组件参数可以直接通过在系统模型的图形部分点击组件图标来进行改变,从而创建同种类型不同结构的组件,因此所建立的组件模型具有通用性,其他系统参数的创建过程与创建组件模型中的过程4)基本一致。

5)创建模型变量:在模型的文本部分创建,系统模型中的变量主要包括了频率f、全局变量拉氏算子s、所研究的传递函数,以及对应的幅值相位等频域参数。

6)建立模型方程:需在关键词equation后建立模型方程,包括频率f与仿真时间的关系式、拉氏算子s与频率f间的关系式s=j2πf、传递函数的定义式以及频域参数的计算式等。

7)检查、编译及仿真设置:检查用于检测模型的变量和方程数,翻译用于分析模型、生成仿真代码和求解器,仿真设置用于对仿真区间、时间步长、积分算法等进行设置,完成后即可开始进行仿真研究。

8)仿真并查看结果:在结果处理方面,MWorks软件提供了创建y(t)、y(x)曲线的功能。此外,还可以将结果数据导出为csv或mat文件,可以通过数据处理软件对得到的结果进一步处理。

通过上述建模过程,在MWorks中建立的流量调节器—管路系统计算模型、单向—管路系统计算模型分别如图6和图7所示。

图6 流量调节器—管路系统计算模型

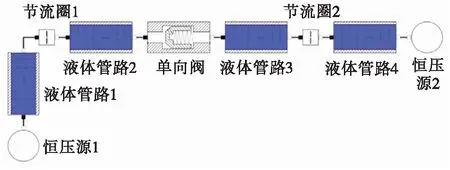
图7 单向—管路系统计算模型

2 计算结果及分析

2.1 流量调节器—管路系统结果分析

某一稳态工况条件下,分别以调节器进口、出口压力为扰动项,在MWorks软件通过模型计算得到出口流量和滑阀位移分别对进、出口压力扰动响应的幅频特性如图8所示。

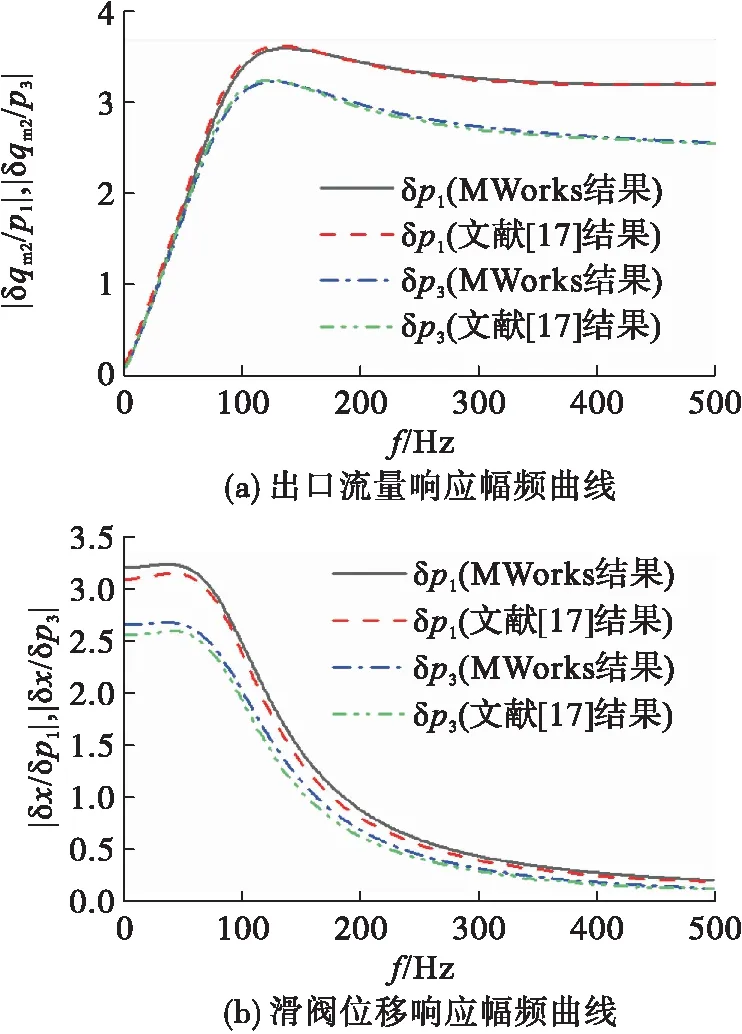
图8 流量调节器对进出口压力扰动响应的幅频特性

通过对比可以看出MWorks与文献[17]中的计算结果误差在10%以内,可以说明在MWorks中建立组件频域模型和开展频域特性研究的合理性。同时,可以看出进、出口压力扰动对调节器状态参数的影响规律相近,只是出口流量、滑阀位移对进口压力脉动响应的无量纲幅值均大于相同频率下出口压力脉动的数值,说明调节器受进口压力脉动的影响更大。

出口流量对进口压力脉动响应的无量纲幅值先随频率的增大而增加,当频率达到150 Hz左右时幅值达到最大值,随着频率的继续增大,幅值降低到稳定数值;滑阀位移对进口压力脉动响应的无量纲幅值则刚好相反。这说明流量调节器具有抗低频干扰的能力,频率较低时调节器出口流量受压力扰动的影响较低。而在较高频率下滑阀位移受压力扰动的影响几乎为零,滑阀口面积为恒定值,这种情况下调节器相当于两个固定节流口的装置。

为了研究加装供应管路的长度对流量调节器—管路系统频域特性的影响,取管路长度分别为1.0、1.5、2.0 m,管路直径为26 mm,计算调节器出口流量、滑阀位移相对管路入口压力的幅频特性如图9所示。

从图9中可以看出,曲线上有若干谐振峰,随着管路长度的增加,各阶谐振峰移向低频区域,而且峰值有所增加。各阶谐振峰值均大于单独考虑流量调节器时的幅值,说明供应管路对调节器的动态特性有很大影响。这些谐振峰在一定程度上体现了系统的固有特性,在某些响应较高的谐振频率附近,可能体现了系统的固有不稳定。

2.2 单向—管路系统结果分析

将单向—管路系统的进出口压力分别设置为13.62 MPa、2.2 MPa,阀芯关闭且速度为0,节流口前压力均为系统进口压力,节流口后压力均为系统出口压力,流量均设为0,来模拟阀芯瞬开过程。系统初始在小流量条件下计算,对应的前后节流圈的流阻系数较大。

在MWorks平台采用四阶Runge-Kutta数值积分法进行求解,时间步长取为20 μs,该初值条件下系统各状态参数的变化曲线如图10所示。

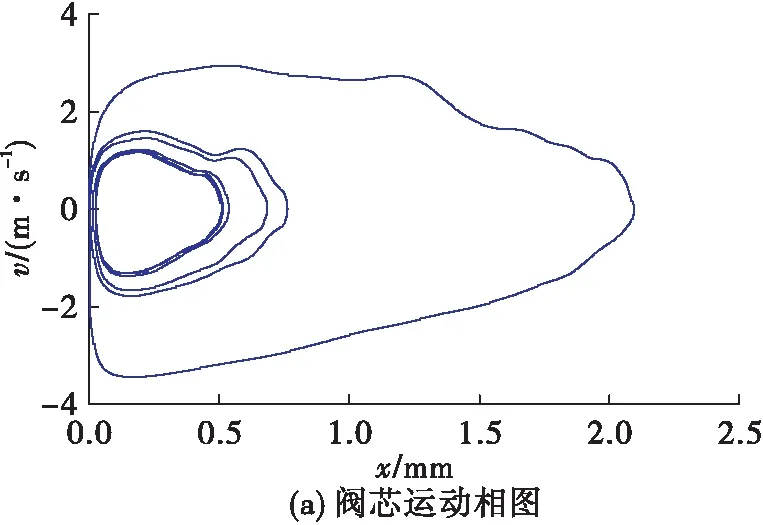
图10 单向—管路系统的参数变化情况

从图10中可以看到,经过一段时间后,系统的各参数达到了等幅振荡状态,阀芯运动相图上形成了一道闭合的极限环。阀芯开度变化的周期约为1.286 ms,折合成频率为777.6 Hz,同时可以看到阀芯在完成1个周期达到零开度前速度小于0,说明阀芯与阀座左端周期碰撞,形成了自激振荡。

从图10 (c)、图10(d)中可以看到,当阀芯趋于关闭时,阀芯流量qmx急剧降低,阀芯入口压力p1迅速升高,出口压力p3迅速降低,在压差力作用下阀芯再次打开,阀芯流量qmx迅速增加,出口压力p3随之增加,而由于流量滞后效应,节流圈流量qm1还在减小,导致阀芯入口压力p1急剧减小,单向阀两端压差降低,在弹簧力作用下阀芯达到最大开度后又趋于关闭,从而维持了系统的自激振荡过程。

综上可以得出单向阀流路系统不稳定的机理是在小的阀芯开度下,微小的阀芯开度波动即可引起阀芯节流口流阻系数很大的变化,从而使得流过阀芯的流量以及阀芯前后的压差随之大幅变化,而大幅变化的压差使得阀芯开度再次变化,此时阀芯与流体运动间的相互作用形成了正反馈,系统的自激振荡不断发展,进入了稳定的极限环。

改变系统状态参数的初值,在各处压力、流量初值均不变的条件下,取阀芯开度、速度分别为较小、较大的初值,计算阀芯的运动相图,如图11所示。与初值为0时的阀芯运动相图对比可以看到,在不同初值下系统最终达到同一个极限环。

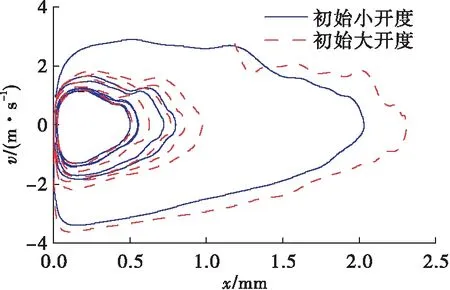
图11 不同初值时的阀芯运动相图

通过静态计算得到系统的平衡点,将各状态参数初值设置在平衡点附近,采用相同的仿真设置,得到的结果如图12所示。从图12中可以看到阀芯开度最终稳定在0.137 6 mm处,速度为0,流量在较小范围内有变化。由此表明当系统初值远离平衡点时,系统是不稳定的并最终达到同一个极限环,而平衡点附近系统各状态参数值会很快达到稳定。这是因为在平衡点附近阀芯受力接近平衡,运动速度较小,且干摩擦力不断阻碍阀芯运动,最终使系统收敛于平衡点,因此可以得出单向阀流路系统在小流量条件下具有平衡点附近局部稳定而大范围不稳定的特征。

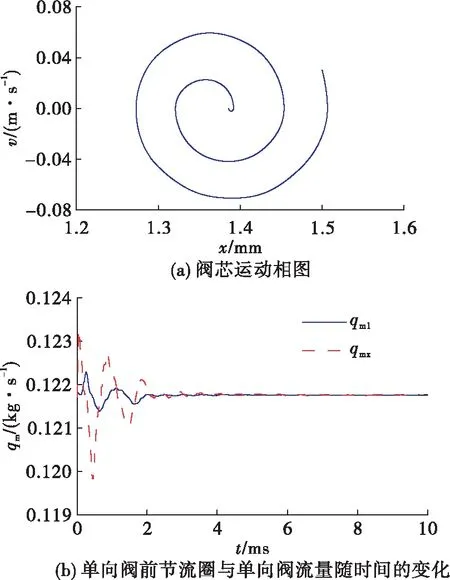
图12 系统局部稳定曲线

为了避免单向阀流路系统出现自激振荡的情况,需要研究工况参数、结构参数等对单向阀流路系统阀芯开启过程的影响规律。

2.2.1 系统压差

首先衡量系统压差对单向阀流路系统自激振荡过程的影响,分别在3组不同的进出口压力下开展系统仿真计算,压力数值如表3所示。系统中各组件状态变量的初始值为远离平衡点的极端状态,即阀芯关闭且速度为0,节流口前压力均为系统进口压力,节流口后压力均为系统出口压力,流量均设为0。计算得到不同系统压差下的自激振荡形成的极限环如图13所示。

表3 3组不同的进出口压力数值

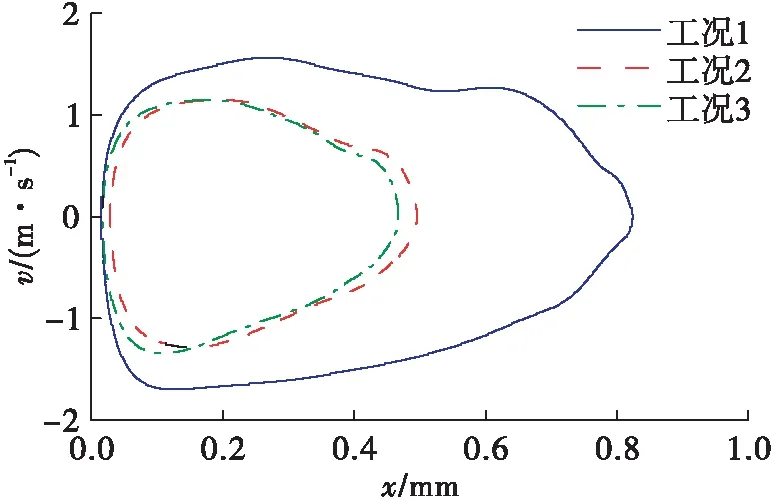
图13 不同系统压差条件对自激振荡极限环的影响

从图13中可以看到,随着系统压差的增大,由阀芯自激振荡形成的极限环扩大,此时状态变量的振荡幅值增加,阀芯碰撞阀座时的速度值也增大。3种不同的系统压差下,阀芯开度变化的周期分别约为1.669、1.286、1.211 ms,折合成自激振荡的频率依次为599.16、777.6、825.76 Hz,说明自激振荡的频率随压差增大而有降低的趋势。

2.2.2 干摩擦力

考虑干摩擦力对以平衡点附近为初值的单向阀流路系统的影响,在进出口压力分别为13.62、2.2 MPa下,通过静态计算选取平衡点附近一点处的参数为状态变量的初始值,分别在有干摩擦力、无干摩擦力条件下开展仿真计算,得到两种条件下的结果如图14所示。可以看到当不考虑阀芯的干摩擦力时,阀芯运动会逐步远离平衡点,而流路振荡的幅值也随之增大。这种情况代表了无干摩擦情况下系统是线性不稳定的,只需微小的扰动就能使整个系统偏离平衡点,即干摩擦力是使系统在平衡点附近达到局部稳定的原因。

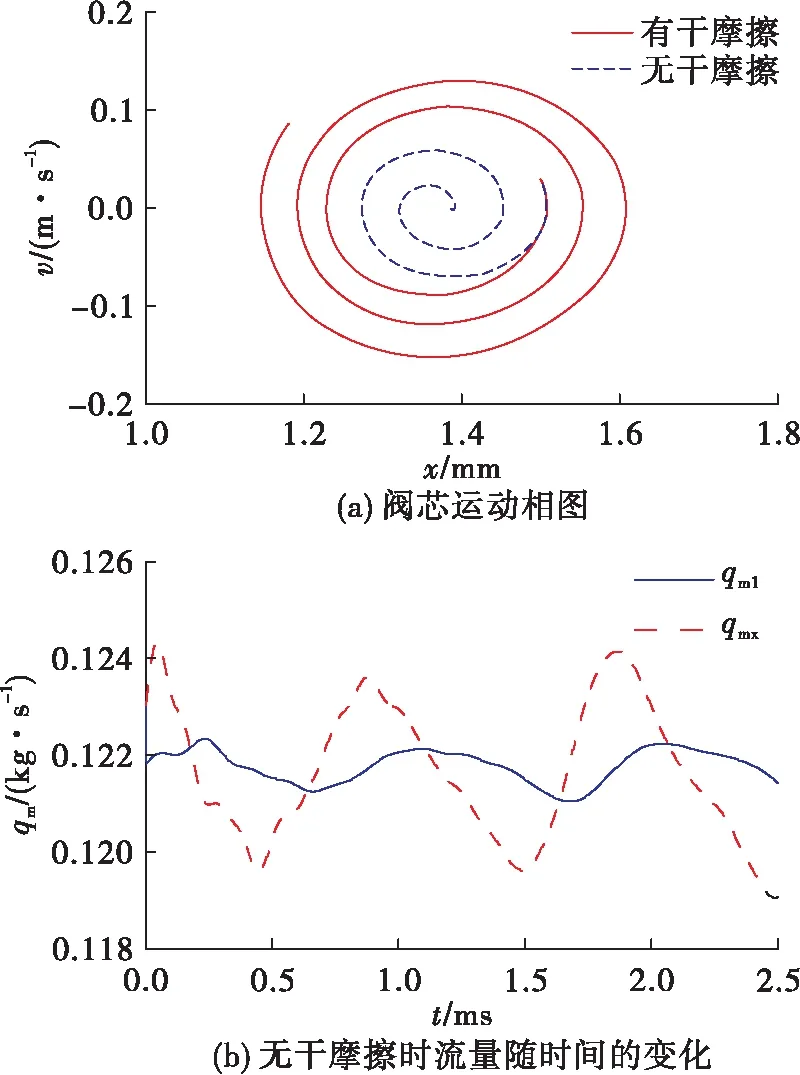
图14 有无干摩擦对单向阀流路系统的影响

综上所述,干摩擦力是单向阀流路系统在小流量条件下具有平衡点附近局部稳定的原因,工况参数对单向阀流路系统的自激振荡过程有所影响,稳态压差增大会使系统状态参数的振荡幅值增加但频率降低。

3 结论

本文在MWorks软件平台上采用Modelica语言进行了流量调节器—管路系统、单向—管路系统的搭建,并研究了流量调节器—管路系统的频率响应特性和单向—管路系统的自激振荡特征及规律,根据计算结果可以得到以下结论。

1)MWorks中可以根据inner/outer关系将拉氏算子s设置为全局变量,并通过建立频率随时间的变化函数,使得同一时刻系统各组件的计算频率相同,从而实现系统频域特性的计算,且建模过程清晰明了,所建立的Modelica模型具有较强的通用性,计算精度满足需求,适用于液体火箭发动机动态特性的研究。

2)流量调节器自身具有抗低频干扰能力,流量调节器连通供应管路后,系统的幅频特性会出现谐振峰,随着管路长度的增加,各阶谐振峰移向低频区域,而且峰值有所增加。这说明流量调节器的滑阀随动响应与供应管路的声学振荡相耦合,滑阀作动对管路在声学频率下的参数脉动起到放大效果,且频率越低放大效果越明显,因此在发动机设计过程中应合理设计流量调节器供应管路的长度,避免因谐振频率与预燃室一阶纵向声学固有频率接近而引起中频耦合振荡。

3)单向阀流路系统在小流量条件下具有平衡点附近局部稳定而大范围不稳定的非线性特点,在阀芯所受的众多作用力中干摩擦力是平衡点附近局部稳定的要素。系统自激振荡形成的极限环是一个具有大范围吸引域的稳定极限环,随着单向阀流路系统进出口压差的增大,阀芯运动形成的极限环会扩大,状态变量振荡幅值增加,而系统自激振荡频率降低。