常用钟型喷管造型、性能及低空使用边界分析

刘阳旻,田 原,马志瑜,杜 宁,丁煜朔

(北京航天动力研究所,北京 100076)

0 引言

液体火箭发动机喷管的主要作用是将在燃烧室中发生剧烈化学反应燃烧产生的高温高压燃气的热能转化为动能,使气流加速,气流对推力室的反作用力产生推力[1]。不同的喷管型面对气流的作用不同,低空喷管型面设计的主要目标是高喷管性能、不流动分离以及避免启动关机段的大侧向力[2-3]。其中喷管性能主要由面积比和型面决定,是否发生流动分离主要由喷管壁面出口压力决定,喷管的内激波会造成启动关机段从FSS(free shock separation)分离模态向RSS(restricted shock separation)分离模态的转换,从而产生大侧向力[4-5]。这三者与型面关系最大,因此喷管型面设计非常重要。

目前工程上基本都使用钟型喷管,它们分别是最大推力喷管[6](thrust optimized contour,TOC)、最优抛物线喷管[7](thrust optimized parabolic,TOP)、截短理想喷管[8](truncated ideal contour,TIC)、压缩截短理想喷管[9](compressed truncated ideal contour,CTIC)。这4类钟型喷管各有优劣。TOC喷管因其高性能优势得到了我国工业部门的采用,但是它的出口压力较低,具有内激波,在避免流动分离和大侧向力上没有优势。TOP喷管因为其在性能和高出口压力的较好协调而得到了欧美航天部门的青睐,航天飞机主发动机(space shuttle main engine,SSME)[10]、火神发动机[11]均采用了TOP喷管,缺点是具有内激波,可能会遇到大侧向力[12]。TIC喷管没有内激波,不会产生大侧向力,性能略逊于TOC喷管,RD-0120等大部分俄罗斯发动机喷管都使用该型面设计,但它的出口压力较低[13]。CTIC喷管可达到与TOC喷管相当的性能,Hoffman认为它在TOC喷管型面无解时是一种优良替代[9],日本LE-7A[14]发动机喷管在设计时为了尽量减小喷管长度而采用了它,其缺点与TOP喷管相同。这说明TOC喷管并非工程上的唯一选择,其余3类钟型喷管也有其自身的突出优点才会被采用。Frey等将TIC喷管和TOP喷管设计方法融合,开发出了TICTOP喷管设计,它融合了两者的优点,具有高出口压力,无内激波[15]。刘亚洲等提出了一种壁面压力控制的钟型喷管造型方法,先截短TOC喷管并规定后段壁面的压力分布,然后使用特征线法反求壁面型线,大大提高了规定燃烧条件下喷管的低空可用面积比[16]。

但是上文提及的新型钟型喷管型面设计方法都没有实际使用经验,并且我国工业部门对非TOC喷管的钟型喷管型面研究较少,对其优化造型方法和特点不够了解。因此本文使用文献[17]中的无旋特征法开发了除TOP喷管以外的喷管造型程序,使用拟抛物线公式构建TOP喷管型面。同时在喷管流场求解上创新性地使用自编的高效喷管轴对称化学动力流场求解器NEABLS[18](nozzle euler and boundary layer solver)对构建的型面进行求解,它的计算原理类似于美国的TDK[19](two-dimensional kinetics)软件,采用特征线法求解欧拉方程,有限差分方法求解可压缩附面层方程,它完整求解一次二维喷管化学动力流场仅需1 min左右,相比全N-S方程求解[20]时间大大减少,精度相当,更适合用来做喷管初步设计和优化设计。因此本文使用NEABLS求解绝热状态下的喷管真空比冲表征喷管性能,求解喷管出口壁面压力表征流动分离界限,然后使用Fluent来进行流动分离仿真验证,从而系统研究了4类传统钟型喷管型面的性能以及低空使用边界上的差异,可供工业部门设计参考。

1 常用钟型喷管型面设计

1.1 TOC喷管型面设计

如图1所示,本文采用Rao氏最大推力喷管设计方法[6],它的原理是假定喷管长度与质量流量一定,求产生最大推力的控制面BDE,引入推力公式时也对外界气压pa进行了规定,图1中BD为右特征线,DE为左特征线,经过变分法推导后得出的公式如下。

图1 最大推力喷管设计示意图

在DE线上,有

(1)

yρv2sin2θtanα=-λ3

(2)

在E点处,有

(3)

计算出从下圆弧段发出的右特征线后,将右特征线上每一点当做D,然后利用式(1)～式(3)和左特征线关系式以及流量平衡关系求出DE线,根据设计需求确定E点后,采用特征线法和流量平衡关系求解壁面型线BE。然而实际计算时,往往为了控制喷管质量选择的设计标准是规定面积比和长度,因此为了扩大程序的求解范围要放松对式(3)的严格求解,即压比通常不严格满足式(3),在规定面积比和长度时,真空条件pa/pe=0通常达不到,这使得设计出的喷管不一定是规定面积比长度下的最大真空比冲喷管。

1.2 TOP喷管型面设计

将喷管喉部半径rt、下游圆弧半径rd、喷管长度l、喷管初始扩张角αi、喷管出口半径re、喷管出口角αe代入抛物线型面拟合公式中便可得到不同的抛物线型面如图2所示,之后要对这些型面进行流场计算以获取喷管性能、流动分离边界等关键参数,再根据设计需求选择TOP喷管型面。

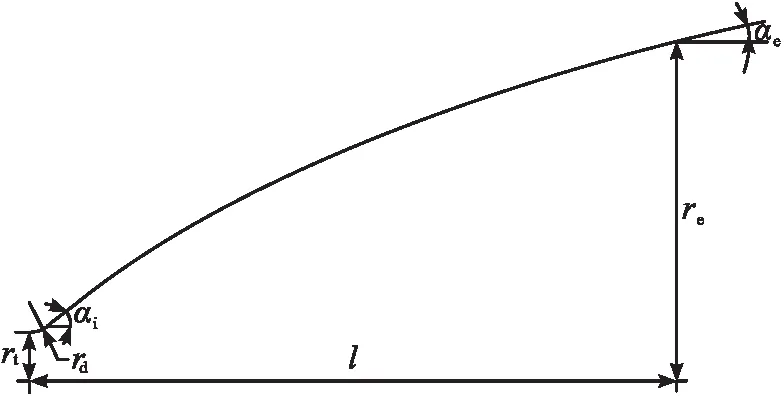
图2 抛物线喷管设计示意图

本文使用SSME喷管抛物线公式[10],它是Rao提出的拟抛物线公式[2]的一种变形,即

(4)

式中以喉部为原点。

1.3 TIC喷管型面设计

TIC喷管设计的前提是理想喷管(ideal contour,IC)设计,理想喷管设计示意图如图3所示。

图3 理想喷管设计示意图

由于理想喷管出口产生均匀平行气流,因此图3中的左特征线DE是一条直线,其上各点流动参数相同。BD是一条从下圆弧段发出的右特征线,故理想喷管设计与Rao氏最大推力喷管类似,实际上Rao氏最大推力喷管控制面BDE上的D点在轴线上设计出来的便是理想喷管。理想喷管设计完毕后,根据设计需求将其截短便是TIC喷管设计。

1.4 CTIC喷管型面设计

CTIC喷管将TIC喷管型面轴向进行线性压缩,然后使线性压缩后的型面与原有圆弧段平滑过渡。本文用的方法是不连续点沿径向和轴向都平移直至与圆弧相切[21],维持了所有压缩段型面的原貌,但是在轴向和径向都会略微偏离设计点,实际计算过程中这个误差不超过1%。CTIC喷管设计如图4所示。

图4 CTIC喷管设计示意图

线性压缩程度由压缩因子确定,压缩因子公式为

(5)

设计时,取不同面积比的基准理想喷管就能设计出不同型面的CTIC喷管,类似于TOP喷管设计,之后仍需对这些不同的型面进行流场计算,根据需求选取最优型面。

2 喷管性能和流动分离计算方法

2.1 喷管性能计算方法

理论上满流的内流场使用自编软件NEABLS求解,它是一个高效的无黏流场结合附面层修正求解器,精确考虑了化学动力效应、扩散效应、附面层效应对喷管性能的影响,使用特征线法求解无黏流场,有限差分方法求解可压缩附面层方程,其详细描述和验证计算可参见文献[18]。它可直接输出满流状态下的喷管真空比冲和出口壁面压力,但由于附面层近似的局限性,无法计算流动分离。它的计算速度极快,单个工况计算时间在40 s左右,结果与CFD相当。

2.2 流动分离计算方法

使用ICEM绘制二维网格,导入Fluent后进行计算,计算域与边界条件参考了文献[22]的设置,计算网格在喷管出口和壁面处加密,计算域和网格如图5和图6所示。

图5 计算域及边界条件

图6 计算网格

图5中除喷管以外的压力进出口边界均取大气压和300 K常温,喷管的压力入口取室压和热力计算得到的总温,喷管壁和转折处小台阶取绝热无滑移壁面,紧接大气入口的壁面取绝热有滑移壁面,取应力为0。将工质当做量热完全气体处理,cp取热力计算得到的燃烧室处的燃气冻结cp,分子量也取热力计算得到的燃烧室处的值,导热率使用分子动力学,黏度使用苏士兰公式,系数取空气所用的系数。湍流模型使用SA一方程模型,保证壁面y+≈1,计算时除湍流输运方程采用一阶格式外,其余方程均采用二阶格式。

2.3 网格无关性及自研求解器NEABLS计算效果验证

在使用特征线法和附面层修正求解器NEABLS求解喷管性能时,喉部初值线点数设置为251点,附面层计算时差分节点数在50点以上,该设置的结果经与文献[18]中SSME比冲及传热的计算结果对比已得到充分验证。

如2.1节所述,NEABLS无法计算流动分离,因此使用FLUENT仿真流动分离,共采用了3套网格对SSME喷管的标准工况进行了仿真,型面参数及燃烧条件均取自文献[22],文献[22]中TDK计算的喷管壁面出口压力为42.124 9 kPa,NEABLS计算得到的壁面出口压力为42.669 8 kPa,与文献[23]结果基本一致,此时在大气压下喷管应处于满流状态,可将CFD与NEABLS计算得到的内流场结果做对比验证。划分网格时以喷管内部的流向网格和径向网格数为参数,3套网格“流向网格数×径向网格数”分别是500×161、900×161、900×251。使用最精细网格CFD计算得到的SSME的流场马赫数云图与NEABLS使用特征线法计算得到的无黏流场马赫数云图如图7所示。

图7 SSME流动分离计算马赫数云图

结果表明CFD与使用特征线法计算无黏流场的NEABLS软件的马赫数云图基本一致,喷管呈现预期的满流状态,仿真结果与设计结果一致,NEABLS目前没有激波追踪模块,全流场使用左特征线和流线构建网格,但是采用了插入临时特征线的方法来提高计算精度,具体做法可见文献[19]。从图7中可以看出其捕捉到了喷管中的内激波,说明只要特征线网格足够密、收敛精度足够高,不加入激波追踪的特征线法也能分辨出激波的存在。

分别使用这3套网格计算得到的壁面压力分布与自研软件NEABLS计算得到的压力分布结果对比图(原点对应喉部)如图8所示。

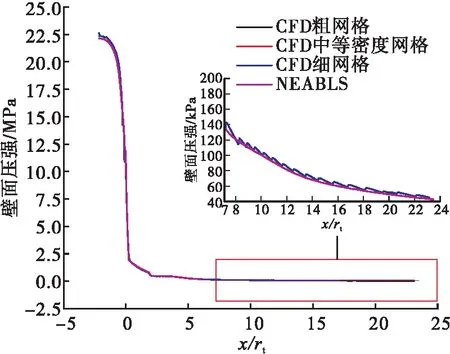
图8 CFD网格无关性验证

由图8可知CFD与NEABLS软件计算得到的壁面压力分布结果基本一致,结合以上的马赫数云图(见图7),本文得到了与文献[24]相同的结论,即在激波强度较低的钟型喷管流场中,没有加入激波追踪方法的特征线法依然可以获得精确的结果,这说明NEABLS计算精度已经足够高,完全可以用作喷管型面优化计算的工具。而CFD采用最精细的网格和采用粗网格结果相差不超过0.5%,因此采用中等密度网格进行仿真计算。

3 计算结果

3.1 相同长度、面积比下4类喷管性能对比

设计输入面积比为49、长度为0.8倍15°锥型喷管长、喉部半径rt为106.2 mm、下游喉部半径为0.6rt、室压10.2 MPa、混合比6.048 5的氢氧发动机喷管。分别用前文所述的4类设计方法进行了设计,并使用NEABLS计算获得喷管性能。

规定面积比和长度,TOC喷管和TIC喷管的型面是唯一确定的,但是此时由式(3)计算出的TOC喷管的压比不为0,这表明它并不是该面积比下的严格真空比冲最大喷管。而TOP喷管和CTIC喷管的设计需要对不同型面进行寻优计算,下面介绍了优化计算的方法和思路。

首先计算TOC喷管得到的喷管出口角为7.828°,喷管初始角为33°,推测TOP喷管的设计输入在这两个值附近,于是将初始角从20°取到40°间隔为1°共21个值,而出口角取了3°、4°、5°、6°、7°、7.5°、7.828°、8°、9°、10°、11°共11个值,组合在一起共计算了231个工况,耗时2.57 h,若使用CFD计算预计耗时约2个月。在设计CTIC喷管时,先是分别以面积比51、53、55、59、69、79、89、99、109、119、129(这些取值和间距可通过试算喷管性能得到)的理想喷管为基础喷管设计了11个喷管,然后计算它们的性能,发现在面积比为69处转折。为了研究在面积比59～69之间是否会出现性能更好的喷管,又额外计算了以面积比71、73、75、77、81、83、85、87的理想喷管为基础喷管设计的CTIC喷管性能。计算出的抛物线喷管真空比冲随进出口角αe、αi变化的云图和CTIC喷管真空比冲随基础理想喷管面积比的变化如图9所示。

图9 TOP喷管和CTIC喷管的真空比冲优化计算

从图9可知:随着进出口角的增大,抛物线喷管比冲先增大后减小;而CTIC喷管比冲则是随着基准理想喷管面积比先增大后减小。这可以从本文所用的特征线法计算公式出发分析,沿左特征线有如下相容关系[19]。

(6)

式中:p为压力;r为径向坐标;θ为流线角;A为化学项相关参数;G仅与马赫数相关;F与θ成反比。

式(6)中A、G、P可认为仅与上游参数相关,因此由式(6)可得流线角越大,流线角变化量越大,压力降低越快,因此喷管扩张段型线整体斜率越小,压力降低越少。而此时压力在壁面的轴向余弦值也在变小,故随着抛物线喷管进出口角的增大或是CTIC喷管基准喷管面积比增大,型面整体倾斜程度增大,先是压力减小的速度低于轴向余弦值增大的速度,两者的乘积(即压力的轴向分量)增大,比冲增加,到了最大点后,压力减小的速度高于轴向余弦值增大的速度,两者的乘积减小,比冲减小。

从图9中可知:真空比冲最大的抛物线喷管出口角αe为9°、初始角αi为37°,于是将该喷管确定为TOP喷管,而以面积比为69的理想喷管构建的CTIC喷管真空比冲最大,它们和TOC、TIC喷管的性能如表1所示。

表1 4类喷管性能

由表1可知,4类喷管性能差距不大,由于此时TOC喷管不是严格解,其比冲反而略低于TOP和CITC喷管,并且从图9(b)中可以发现CTIC喷管在达到与TOC喷管相当性能的设计参数后再细化参数进行计算取得的收益很小。

3.2 4类喷管低空使用界限对比

通过分析出口壁面压力来对比它们的低空使用界限,先给出前面NEABLS计算出的抛物线喷管出口壁面压力随进出口角αe、αi变化的云图和CTIC喷管出口壁面压力随基础理想喷管面积比的变化如图10所示。

图10 TOP喷管和CTIC喷管的壁面出口压力优化计算

从图10中可以发现,抛物线喷管的出口壁面压力随进出口角αi、αe减小而增加,CTIC喷管的出口壁面压力随基础理想喷管面积比增大而减小,与3.1节中分析一致,而CTIC喷管在最优设计点附近出口壁面压力有时会随基准喷管面积比的增大而略微增大,这主要考虑型面计算精度和NEABLS软件计算误差的综合影响,并不影响主要结论。TOC、TIC、TOP、最优比冲CTIC喷管的出口壁面压力如表2所示。

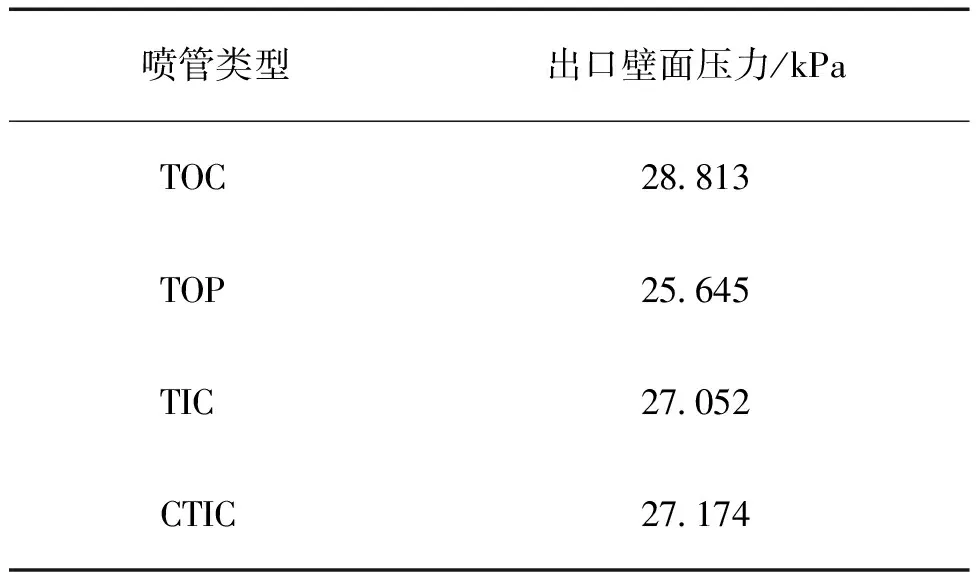
表2 4类喷管出口壁面压力

由表2可知,若仅追求真空比冲最大,此时4类喷管出口壁面压力均低于31.41 kPa(0.3 atm),处于即将发生流动分离或者弱分离的状态。参考SSME喷管的设计思路,适当减小抛物线喷管的进出口角(αi,αe)为(35,3),出口壁面压力提升为41.341 kPa,真空比冲仍可达4.395 977 km/s,相比TOP喷管比冲仅减小0.3%,提高了可靠性。而选用面积比为51的理想喷管构建出的CTIC喷管出口壁面压力也可达38.618 kPa,但是真空比冲仅为4.368 854 km/s。

为了进一步分析抛物线喷管和CTIC喷管的压力可调性,进而增大可用的设计面积比,进行了面积比为59,0.8倍15°钟型喷管长度的喷管设计,其中抛物线喷管进出口角选(35,3)、CTIC喷管基础理想喷管面积比取61和63,它们的真空比冲和出口壁面压力如表3所示。

表3 面积比为59的喷管出口壁面压力与真空比冲

从表3中可以看出:增大面积比后,TOC喷管和TIC喷管压力均过低,不适宜低空工作;CTIC61喷管压力虽高但是真空比冲太低;CTIC63喷管相比面积比为49的TOC喷管提高15.408 m/s,出口壁面压力与之相当;TOP(35,3)喷管比冲相比面积比为49的TOC喷管提高了20.954 m/s,壁面压力超过了31.411 kPa(0.31 atm)。

3.3 4类喷管流动分离界限对比

为了验证前文所提的低空使用界限,使用2.2节中所述的方法对本文设计的各喷管进行了流动分离仿真,理论上满流的面积比为49的TOP(35,3)喷管马赫数云图如图11所示。对比了设计的其他喷管的流动分离图像(见图12),其中面积比为59的TOC、TIC喷管,面积比为49的TOP喷管,出口压力过低,不再对它们进行仿真,使用面积比为61的理想喷管构建的面积比为59的CTIC喷管比冲相对其他喷管太低,也不对其进行仿真。

图11 面积比为49,35°入口角、3°出口角抛物线喷管马赫数云图

图12 各类喷管流动分离仿真图像

由图12可知,无内激波的TIC喷管或是内激波在轴线上反射的喷管呈现马赫盘结构,其余内激波未反射的喷管均显示出了帽状激波结构。出口压力较低的面积比为49的TOC、TIC、最优比冲CTIC喷管以及以面积比为63的理想喷管设计的面积比为59的CTIC喷管流动分离程度都非常小,不影响实际使用,出口壁面压力较高的面积比为49的CTIC51喷管和面积比为59的TOP(35,3)喷管则呈现了满流状态,这说明通过使用NEABLS计算出口壁面压力判断流动分离状态是可行的,并且通过调节型面,CTIC喷管和TOP喷管都可以使用更大的长度和面积比来进行设计,因此在进行CTIC喷管和TOP喷管设计时,可以将长度和面积比也作为变量来进一步优化设计型面。

4 结论

本文采用无旋特征线法和拟抛物线公式设计各类喷管,使用自编的基于特征线法和附面层修正算法求解器NEABLS求解喷管性能和出口壁面压力,采用FLUENT软件计算流动分离,得到了以下结论。

1)自编求解器NEABLS求解喷管性能和流场的结果非常准确,是一个比较好的喷管设计优化工具。

2)由于TOC喷管在求解型面时难以满足所有约束条件,规定面积比和长度时,最优性能的CTIC喷管、TOP喷管和TIC喷管的性能都有可能高于TOC喷管。

3)若不希望内激波出现,则应选择TIC喷管。

4)喷管面积比和长度相同时,4类喷管性能相似,若追求设计效率,建议采用TOC或TIC喷管。

5)TOP喷管减小进口角或者出口角,CTIC喷管减小压缩因子,均可增大其壁面出口压力,提高喷管抗流动分离能力,进而提高低空可用面积比,因此TOP喷管和CTIC喷管可以将面积比和长度也作为优化设计的变量来进一步对喷管型面进行优化设计。设计目标是不流动分离且比冲最大时,建议考虑这两种型面,但是它们设计计算量较大,需要如NEABLS这样高效准确的喷管流场求解器辅助才能迅速完成。