基于变分模态分解的燃烧室热声振荡衰减系数辨识

樊志伟,钟 战,李 庚,聂万胜,何 博

(航天工程大学 宇航科学与技术系,北京 101400)

0 引言

高频燃烧不稳定源自燃烧室内燃烧过程与声学振荡的耦合[1-2],一旦发生将在几秒内破坏整个发动机。为尽量避免液体火箭发动机使用过程中出现燃烧不稳定,提高工作可靠性,通常需要在其研制阶段开展大量燃烧稳定性裕度试验评估工作。目前,评估燃烧稳定性裕度主要基于如下两种技术指标参数[3-4]:①燃烧室工作过程对人为扰动响应的驰豫时间[5];②燃烧室容腔谐振频率的振荡衰减率。其中,前者是国内外早期试验评估通常使用的方法,但需要外部激励装置诱导激励燃烧室出现高幅值压力振荡,会对发动机结构产生不利影响;后者则仅需要发动机稳定燃烧阶段的燃烧室压力监测数据,是当前极具发展前景的一种燃烧稳定性裕度评估方法。

对于燃烧室热声振荡衰减率的辨识,其基本原理是将其稳定燃烧阶段的系统动力学建模为不同复杂程度振子模型方程[6],进而通过系统辨识方法从燃烧室脉动压力数据中辨识出模型方程衰减系数,从而判定发动机燃烧稳定性裕度。Lieuwen利用压力数据的自相关函数计算出燃烧系统衰减系数,从时域对非线性耦合振子模型的衰减系数进行了辨识[7]。Stadlmair等采用贝叶斯统计方法,从单特征模态拓展到了多模态的衰减系数辨识[8]。Yi等利用维纳辛钦定理将时域方法变换到了频域,拟合脉动压力功率谱得到衰减系数[9]。Noiray等基于噪声相干共振现象,将系统模型建模为随机噪声激励的范德波尔方程,利用压力信号概率密度函数建立了系统模型的福克-普朗克方程,最终通过求解方程的Kramers-Moyal系数拟合出系统衰减系数[10-11]。Boujo等通过引入伴随优化方法修正了Noiray方法中因有限采样时间效应带来的辨识误差,进一步提高了辨识精度[12]。

然而,衰减系数辨识方法中误差影响最大的环节是获取燃烧室热声谐振模态。目前对于燃烧室内谐振模态信息的提取主要采用带通滤波方法,这种方法需要预先确定带通滤波中心频率与滤波宽度。但是,燃烧室稳定噪声燃烧阶段的中心频率通常难以通过理论模型获取,因此使用理论声学谐振频率近似替代中心频率会存在较大误差,从而影响辨识结果精度。此外,带通滤波宽度的选取也会对衰减系数辨识结果产生重要影响[13]。杨尚荣等提出了一种基于非线性最小二乘法的滤波参数计算方法,然而该方法仅适用于单个谐振模态的分离辨识,对两邻近模态混叠情况下分离辨识仍存在不足[14]。

本文基于随机白噪声驱动的二阶非线性振子模型,对理论模型仿真数据和针栓式模型发动机热试车数据进行分析,重点比较了现有带通滤波方法与变分模态分解算法的优劣,验证了变分模态分解算法的适用性与准确性,并将其应用于模型发动机试验结果处理,为液体火箭发动机燃烧稳定性裕度评估提供参考。

1 系统模型与辨识方法

1.1 燃烧室热声模型

目前对燃烧稳定性研究表明:燃烧不稳定是火焰、流场和声场间非线性耦合的结果,而液体火箭发动机的高频燃烧不稳定大多是火焰与声场之间的热声耦合导致的[1]。所以,燃烧不稳定低阶动力学模型通常主要考虑声场与火焰热释放之间的耦合,而将湍流等流场影响简化为随机白噪声项,则热声耦合振荡模型可用如下随机振子方程描述。

(1)

式中:p′(x,t)为时间t位置x处的脉动压力;ηi和ψi分别为第i阶声模态的幅值和振型;Dε(t)为燃烧室压力振荡中湍流引起的白噪声扰动,D为噪声强度,ε(t)为单位高斯白噪声;f为火焰热释放对压力振荡幅值的反馈函数;αi为声模态衰减系数;ω为角频率。

(2)

式(2)中,当v<0时系统处于线性稳定状态。由此可知,根据辨识得出的衰减系数v与0之间的距离即可评定燃烧装置的燃烧稳定性裕度。

1.2 模态提取方法

衰减系数辨识方法中最重要的就是特征模态的获取,而前期研究表明:带通滤波参数选取对辨识精度有较大影响,特别是当处于稳定燃烧阶段,无法精准获取燃烧室内热声耦合频率,进而影响滤波宽度的选择[13]。现有辨识方法采用的是将燃烧室固有声学频率作为特征模态中心频率,进而测算合适的滤波宽度,以此来获取特征模态信息。

然而燃烧噪声阶段,燃烧室压力监测信号为宽频振荡,较难选择中心频率。另外带通滤波宽度也对衰减系数辨识有严重影响。当带通滤波宽度较小时,带通滤波提取的模态信息会丢失部分热声耦合模态从而导致辨识精度下降;而带通滤波宽度过大时,带通滤波提取的模态信息会包含多个特征模态信息从而导致辨识精度下降。所以得到准确可靠的热声耦合模态信息不仅要求包含确定的中心频率,还要求提取模态信息在频谱上存在一定宽度,以包含所有与该模态耦合的湍流噪声信息。

随着信号处理方法的发展,经验模态分解[15](empirical mode decomposition,EMD)、变分模态分解[16](variational mode decomposition,VMD)、局部均值分解[17](local mean decomposition,LMD)等方法逐渐应用于时间序列分解中,然而EMD、LMD方法都存在模态混叠、边界效应和噪声鲁棒性弱等不足,而VMD方法虽然具有良好的噪声鲁棒性,但由于其需要预先设定好分解层数,致使分解结果可能存在过分解或欠分解情况。本文采用文献[18]提出的基于峭度的VMD分解方法计算分解模态中的最大相关分量的峭度值,当峭度值达到最大时停止分解,最终得到最优模态分解结果。

变分模态分解方法将原始信号分解成n个限制带宽的本征模态函数(intrinsic mode function,IMF),表示为

un(t)=An(t)cos[ωn(t)]

(3)

式中:un(t)为分解得到的n个IMF;An(t)为un(t)的瞬时幅值;ωn(t)为un(t)的瞬时频率。每个分量在中心频率处集中,可用高斯平滑调制信号来估算带宽,由于VMD分解的稀疏性,分解时可将其转换为

(4)

为解决上述的约束最优化问题,将约束变分问题转换为非约束变分问题,添加二次惩罚项和拉格朗日因子,得到如下增广拉格朗日函数以求上述问题的最优解。

(5)

式中:α为乘法因子;λ为拉格朗日因子。

利用变分模态分解方法将原始信号分解为K个IMF,过程如下。

1)初始化{uk}、{ωk}、λ1为0。

(6)

3)对所有ω≥0,更新泛函ωk,即

(7)

4)对所有ω≥0,更新拉格朗日因子λ,即

(8)

5)重复循环步骤2)～4),直到满足如下约束条件

(9)

式中:τ为噪声容限;K为预设分解层数。

从分解过程可以看出分解层数与噪声容限对分解结果影响最大。基于峭度的分解层数K确定方法是以最大相关IMF的峭度作为对照依据,以峭度最大作为循环截止条件来确定K的最优解。具体步骤如下。

2)计算ui(t)与原始信号x(t)的相关系数,得到最大相关分量uj(t)。

4)重复步骤1)～3),直到找到峭度最大时的分解层数K。

在确定分解层数后,利用残差指数REI确定噪声容限,在τ∈[0,1]范围下选择残差最小的噪声容限τ。残差指数计算式为

(10)

1.3 时/频域衰减系数辨识方法

对式(2)进行傅里叶变换并取模的平方后,可得到幅值方程的功率谱函数为

(11)

式中:ωi为特征模态的角频率。

系统参数D、v可由压力时间序列辨识得到,即频域衰减系数辨识方法。

根据维纳—辛钦定理可得时域计算的自相关函数与频域计算的功率谱Sη(ω)的关系为

(12)

则可得到幅值方程的自相关函数为

(13)

由于线性衰减系数v远小于角频率ωi,则自相关函数第二项可忽略,由此可得

(14)

由式(14)可知自相关函数幅值在频率ωi附近振荡,且幅值成指数衰减,衰减率为线性衰减系数v,由此可得线性衰减系数,即时域的衰减系数辨识方法。

2 结果与讨论

2.1 模态提取与算法验证

理论验证信号采用非线性耦合振子模型,模型方程为式(2),设定模型参数如表1所示,需辨识的信号由3种不同衰减率模拟信号叠加而成,数值模拟时间为10 s,采样频率为10 kHz。

表1 数值模拟信号系统参数

图1为3种指定参数模拟信号叠加后的幅值与频谱图。

图1 数值模拟信号及其频谱图

图2为带通滤波中心频率选择影响,当带通滤波宽度选取为中心频率的20%时,改变带通滤波中心频率,可见随着中心频率选取从1.0～1.2 kHz,频域方法辨识结果越来越向模态3靠近;时域方法辨识结果先减小,然后趋于模态3的预设衰减系数值(-0.05),误差越来越大,逐渐偏离相对应的模拟信号预设衰减系数。其中,时域方法先降低是因为2个相近模态(0.9 kHz、1.0 kHz)之间的混叠效应。

图2 中心频率对系统辨识结果影响

图3为带通滤波宽度对模拟信号的辨识结果影响,可见时域方法辨识结果先增大后减小,最后仍存在一定误差,频域方法辨识结果一直比较稳定。这是因为时域方法受滤波宽度影响较大,起初滤波宽度较小,模态2(1.0 kHz)只有部分信息进行辨识;进而因模态1(0.9 kHz)与模态2(1.0 kHz)两者中心频率相近,滤波宽度增大会将模态1的影响引入辨识结果中;最后随着滤波宽度继续加大,模态3(1.2 kHz)也影响着辨识结果。频域方法辨识结果较好是因为中心频率不变,滤波宽度影响程度较小。

图3 滤波宽度对系统辨识结果影响

在传统模态提取方法中,频域方法对中心频率的选取比较敏感,时域方法则需要合适的中心频率与滤波宽度。然而在燃烧噪声阶段,燃烧室压力表现为以固有频率为中心的宽频振荡,燃烧噪声自身的随机性会对辨识结果有较大影响。因此,准确可靠的模态提取方法不仅需要准确的中心频率,也需要一定的频带宽度以包含所有模态信息。

图4为本文VMD算法处理的结果。处理VMD分解得到的结果如表2所示,可见VMD算法可以高效分离得到中心频率与模态信号,所得的模态经过时/频域方法辨识后与带通滤波结果误差较小,可以使用基于峭度最大的变分模态分解算法处理压力信号,与带通滤波方法相比,变分模态分解可以自动计算得到中心频率及信号,无需先验的热声谐振频率。

图4 VMD分离模态结果

表2 VMD与带通滤波方法辨识结果

2.2 试车数据与验证

试验发动机采用气氧/乙醇作为推进剂,点火过程利用火花塞来启动发动机,喷嘴类型为针栓式,试验工况设置为:氧化剂(O2,300 K)为112 g/s,燃料(质量分数为50%的乙醇水溶液,300 K)为218 g/s,氧燃比为0.51;该工况下燃烧室内总温1 506 K,声速为910 m/s,模型燃烧室为圆筒形结构,燃烧室直径为70 mm,长度为350 mm,收缩段长度为20 mm,通过计算可得1阶纵向声学固有频率为1.264 kHz,2阶 为2.528 kHz,4阶为5.056 kHz。压力传感器选用一个采样频率为125 kHz的Kistler 6043A动压传感器,脉动压力测点距喷注面板平面15 mm。

图5为燃烧室脉动压力监测信号图,从6.1 s开始进行点火,在6.2～7.2 s之间为燃烧阶段,7.2 s时刻停止供应氧气,燃烧持续时间约1.0 s,期间燃烧室内压力约为1.0 MPa,由放大图可知,发动机处于稳定燃烧状态。为保证实验安全,发动机点火在富氧条件下进行,熄灭在富燃条件进行。

图5 燃烧室动态压力监测图

图6为燃烧室压力功率谱密度,可见在稳定燃烧阶段(6.2～7.2 s)存在2个凸频,在频率2.534 kHz、4.814 kHz附近显示宽频燃烧振荡,分别对应理论计算出的燃烧室2阶纵向、4阶纵向声模态。

图6 燃烧室压力信号功率谱密度

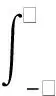
图7为VMD算法对脉动压力数据的处理结果,经过计算:分离模态数K取值为9,噪声容限τ为0.92,共分离出9个本征模态函数,中心频率分别为0.195 kHz、2.510 kHz、3.710 kHz、4.882 kHz、7.421 kHz、10.156 kHz、20.210 kHz、22.613 kHz、32.738 kHz,其中模态2、模态4的中心频率(2.510 kHz、4.882 kHz)与燃烧室固有2阶纵向声频率(2.528 kHz)和4阶纵向声频率(5.056 kHz)相近,且与压力信号功率谱密度图中2个宽频凸峰相近(2.534 kHz、4.814 kHz),可以看出VMD算法可准确地分离得到谐振模态中心频率。

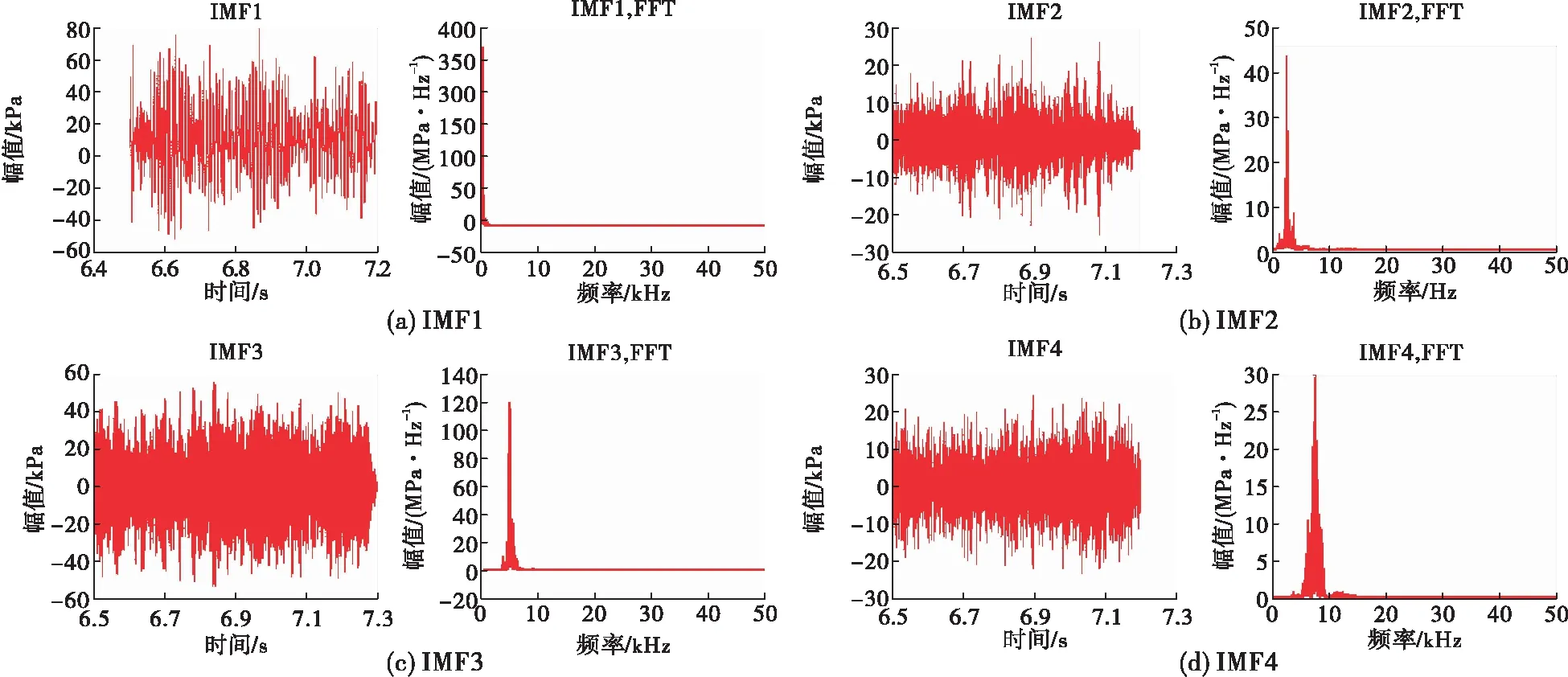
图7 VMD分离模态结果

进而对IMF2和IMF4进行衰减系数辨识,辨识结果如表3所示。

表3 VMD辨识结果

图8为滤波宽度对线性衰减系数影响,随着滤波宽度增加,衰减系数随之减小。所以在带通滤波宽度为中心频率的30%时,衰减系数变化基本稳定,因此时域、频域方法中带通滤波宽度均选择为中心频率的30%。

图8 滤波宽度对系统辨识结果影响

进而对滤波结果进行衰减系数辨识,所得结果与VMD方法所得结果对比如表4所示,对比结果可得无论2阶还是4阶模态的衰减系数,时域方法所得结果相差较小,频域方法所得结果差异相对较大,具体表现在基于VMD方法滤波后的频域结果更高,主要是因为VMD滤波所得的频带宽度更大。

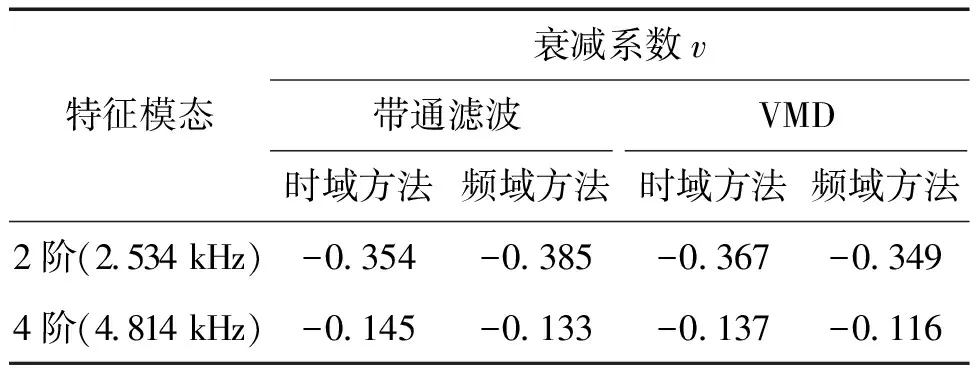
表4 VMD与带通滤波方法辨识结果

图9为衰减系数随时间变化图,对发动机稳定燃烧阶段数据进行滑窗切片处理(滑窗宽度为0.20 s,前进步长为0.01 s),对切片数据进行衰减系数辨识,由此可见衰减系数在稳定燃烧阶段保持稳定,2阶纵向模态在开机表现出较强的不稳定趋势,4阶纵向模态在启停期间并未有明显不稳定趋势。出现这种现象的原因是在启动点火阶段,燃烧室燃料分布不均匀,还未形成稳定燃烧,所以未能形成热声耦合共振场[19-20],得到的衰减系数本质上反映了燃烧室结构的频率选择性。

图9 衰减系数随时间变化

3 结论

本文开展了基于变分模态分解的燃烧室热声振荡衰减系数辨识研究,基于理论模型仿真数据进行验证,并应用在模型发动机热试车数据处理中,得出以下结论。

1)基于最大峭度准则的变分模态分解可以减小现有辨识方法中中心频率选择的任意性,有效得出燃烧室热声谐振频率,提高计算精度。

2)模型发动机试车工况为稳定燃烧工况,2阶纵向模态衰减系数为-0.35,4阶纵向模态衰减系数为-0.13,同时变分模态分解算法与带通滤波方法所得结果差异体现在频域方法结果,是由变分模态分解算法滤波后频带宽度较大所致。