微项目教学:初中数学复习课思维转型路径

[摘 要] 文章以“二次函数”单元复习课为例,阐述“微项目教学”在单元复习课的实践,指出“微项目教学”的单元复习课能更好地串联知识、构建体系,聚焦主线、升华思维,培育学生的数学核心素养.
[关键词] 微项目教学;微项目任务;单元复习
单元复习,以知识梳理和解题教学为主,这样的复习,学生对知识点的掌握是没有问题的,但从整体来看,学生缺乏对知识的整体建构,一做综合题就容易思路混乱,不知从何处开始思考,往往束手无策. 如何让一堂复习课充满活力,让学生有所收获?笔者认为,实施“微项目教学”的复习课,能帮助学生建构知识体系,学会分析问题,寻求解决问题的路径,从而找到思维的突破点,提升数学素养[1].
项目学习理念一般被认为起源于杜威的“做中学”及建构主义思想,“微项目教学”的单元复习课旨在帮助学生在掌握基础知识的前提下,建构知识网络,感悟思想方法,重视思维培养,落实素养提升. 下面笔者以“二次函数”的复习课为例,依托结构建立、模型提炼、题目编拟、拓展探究四类微项目,进行复习课教学,与大家交流.
“微项目任务”下的教学目标
(1)通过设置“微项目任务”,构建二次函数图象和性质的知识体系.
(2)通过设置“微项目任务”,从数和形的角度理解二次函数的图象和性质.
(3)通过设置“微项目任务”,理解二次函数、一元二次方程、一元二次不等式之间的关系[2].
“微项目任务”下的教学过程
1. 设计“微项目任务”,建构知识体系
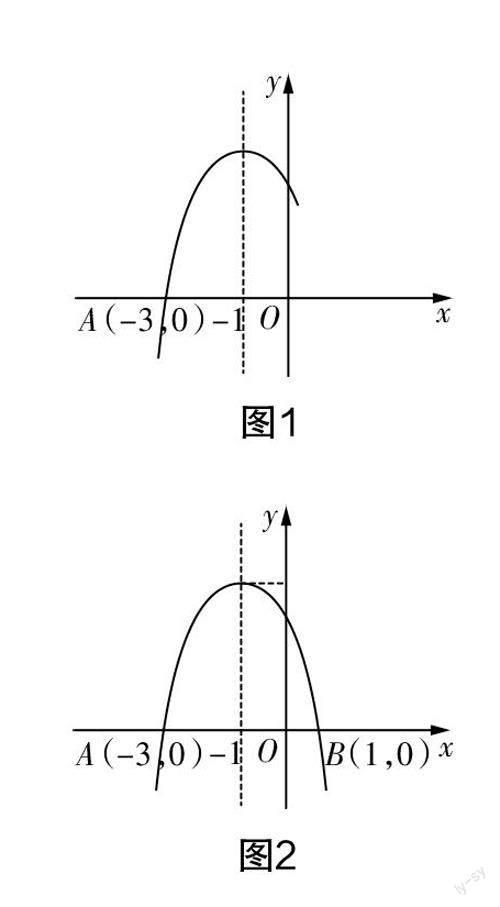
复习课的问题引入应基于学生已有的认知水平,让学生在复习中串联知识,建构知识体系. 为此,我们可以设计如下结构建立类“微项目任务”:二次函数y=a(x+1)2+4(a≠0)的部分图象如图1所示,从图中你能得到哪些信息?这里涉及二次函数的哪些知识?小组交流并画出本章的知识结构.
设计意图 设置开放性问题,从图象入手,由形到数,多视角引发学生思考,建立知识体系,实现不同的学生获得不同的体验.
教学示范 学生思考,教师巡视并指导,从学情(学生写的情况)出发,变教学为导学,帮助学生建立数与形的密切联系. 通过交流,学生发现如下信息.
(1)函数图象开口向下.
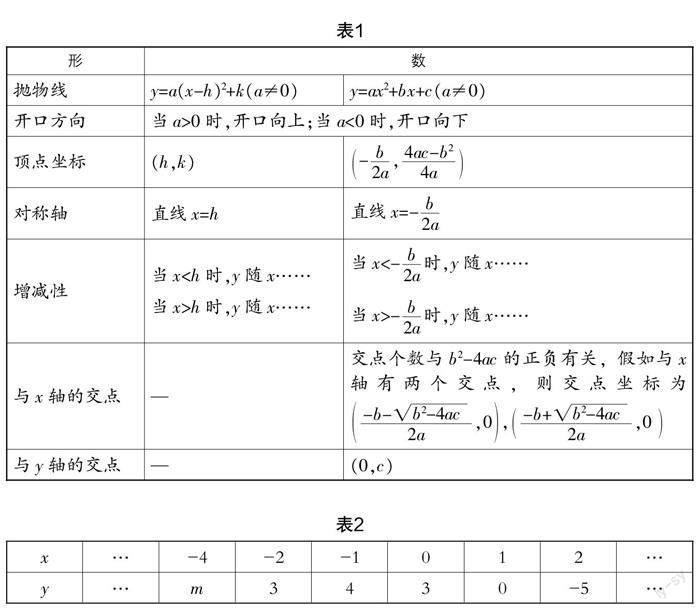
(2)函数图象的对称轴是直线x=-1,把函数图象补充完整(如图2所示)后发现,函数图象与x轴的两个交点是A(-3,0),B(1,0).
(3)函数图象的顶点坐标是(-1,4),通过计算可得到a=-1,从而得到函數的表达式为y=-(x+1)2+4= -x2-2x+3,还可以求出函数图象与y轴的交点是(0,3).
(4)从函数图象可以看出单调性:当x<-1时,y随x的增大而增大;当x>-1时,y随x的增大而减小;当x=-1时函数取得最大值4.
(5)当-3<x<1时,y>0;当x>1或x<-3时,y<0;当x=1或x=-3时,y=0.
由此可得二次函数的知识结构如表1所示.
2. 设计“微项目任务”,进行模型提炼
以学定教. 学生在前面的学习过程中已经积累了大量的经验,也遇到了许多困难,教师可设计如下模型提炼类“微项目任务”:二次函数y=ax2+bx+c(a≠0)中y与x的部分对应值如表2所示.
(1)求m的值;
(2)将该函数的图象上下平移,能否经过原点?左右平移呢?
设计意图 设计第(1)问的目的是告诉学生,不同的解题角度,会带来不同的解题速度. 用待定系数法求函数的表达式时,三种不同的设法,解题速度不同,复杂程度也不同. 当然,最简单的是通过对称直接求出m的值为-5. 设计第(2)问的目的是复习二次函数的平移,让学生理解二次函数图象的平移就是特殊点(如顶点、与坐标轴的交点)的平移.
教学示范 对于第(1)问,可让学生先做,教师巡视,发现、收集不同的解法,展示这些解法后一一点评. 解法1,用待定系数法求出函数的表达式为y=-x2-2x+3,从而求出m的值,其中用待定系数法求函数表达式时选取的点不同,解决问题时的复杂程度也不同. 解法2,直接通过函数图象的对称性得到m的值,简单方便.
对于第(2)问,还是让学生先做,教师及时点评. 解法1,考虑到二次函数图象与y轴的交点是(0,3),所以二次函数的图象直接向下平移3个单位长度即可经过原点;考虑到该二次函数图象与x轴的两个交点是(-3,0)和(1,0),所以二次函数的图象直接向右平移3个单位长度或者向左平移1个单位长度即可经过原点. 解法2,画出函数图象,有的学生还发现这就是上一个任务中的二次函数. 通过完成模型提炼类“微项目任务”,学生知道解决二次函数问题时,不应急着求出表达式,而应多关注图象自身的特征,如对称性和特殊点,从而灵活解题.
3. 设计“微项目任务”,实现思维创新
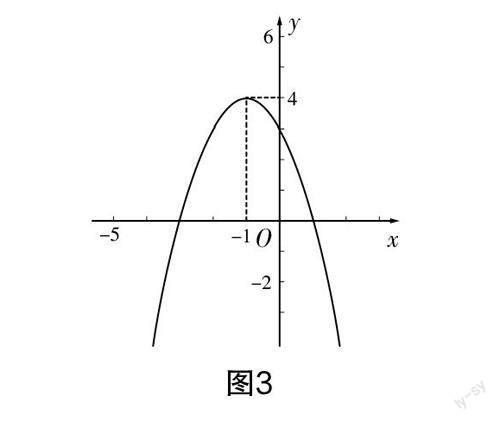
复习课不单单是帮助学生解决问题,更重要的是引导学生善于提出问题. 如刚刚完成模型提炼类“微项目任务”后,教师可继续设计题目编拟类“微项目任务”:观察如图3所示的二次函数图象,添加一个条件,编写一个题目,并和小组同学一起解决.
设计意图 通过解决此类“微项目任务”,学生能体会到重点知识的重点考法,从而提升思维能力.
教学示范 在这里,学生编拟的试题非常精彩,如有学生编了这样一道题:
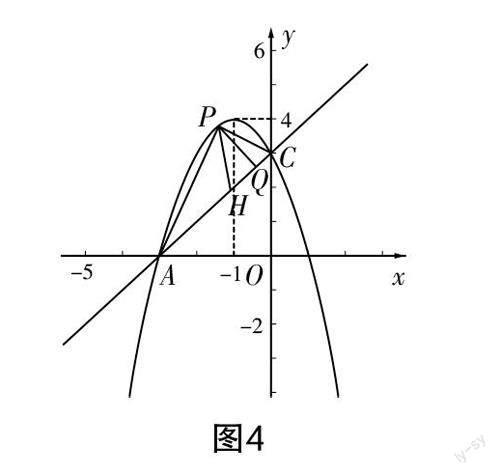
已知如图4所示的二次函数图象和直线AC:y=x+3.
(1)求抛物线和直线的交点坐标;
(2)将这条直线向上平移n(n>0)个单位长度,若平移后得到的新直线与抛物线依然有交点,求n的取值范围.
经过教师的引导,学生编出了第(3)问,即观察图形,利用线段PH,你能解决哪些最值问题?各小问的具体解析如下. 第(1)问求交点坐标,只要求出A,C两点的坐标即可;对于第(2)问,可先求出抛物线的解析式,并设新直线为y=x+3+n,然后联立方程组,转化为关于x的一元二次方程. 因为有交点,所以只需要Δ≥0即可;第(3)问是由线段PH引起的一系列线段和三角形面积的最值问题. 此题的设计是把问题转化为求方程的解,转化为最值问题,涉及化斜为直的思想,这一直是我们平时教学中所强调的,现在学生都能自己命题了,可见他们对知识掌握得非常扎实.
4. 设计“微项目任务”,提升迁移运用能力
对于复习课,教师不仅要关注学生现阶段的知识,还要引导学生拓展研究,解决综合性问题,拓宽学生的视野,提升学生的运用能力和迁移能力. 基于此,教师可设计一些新定义或新情境试题,引导学生现学现用,解决综合问题. 如教师可设计如下拓展探究类“微项目任务”.
定义:若二次函数y=ax2+bx+c(ac≠0)与x轴的两个不同的交点A和B的横坐标分别为x,x,与y轴的交点是(0,c),若x,x中存在一个值,满足x=-c或x=-c,则称该函数为拟和谐函数.如二次函数y=-x2-2x+3就是一个拟和谐函数.
(1)请写出一个拟和谐函数.
(2)请探究拟和谐函数y=ax2+bx+c(ac≠0)表达式中a,b,c之间的关系.
(3)拟和谐函数y=-x2+bx+3与x轴交于A,B两点,与一次函数y=x+3交于A,C两点. ①求b的值;②若M是点B左侧抛物线上的点,连接BM与直线AC交于点N,且BN ∶ MN=5 ∶ 1,求点M的坐标.
设计意图 设计该“微项目任务”,一方面考查学生的阅读能力和信息提取能力,另一方面旨在通过此项目任务的解决,让学生对数学思想(主要是从特殊到一般、类比、转化)有更深刻的认识,并会灵活运用.
教学示范 让学生阅读,提取有用信息,并独立完成,然后小组讨论解决.
“微项目任务”下的教学评价
1. 确立评价工具
评价可以促反思,反馈教学效果,以便下次进行教学改进,所以评价也是教学不可缺少的环节之一. 在“微项目”教学中,评价的工具笔者认为依然是教学目标,让“教、学、评”实现统一,强化教学目标的达成. 依据教学目标,笔者在“二次函数”单元复习课设置了如表3所示的自我评价表.
2. 实施评价教学
教学评价的实施可在课堂结束前5分钟进行,教师可让学生根据自我评价表,给自己打分,然后小组交流,最后班级交流. 在这个过程中,教师积极引导学生在客观评价自我的基础上打分,学生则在此过程中反思自己,和同伴分享收获和疑问. 本节复习课,笔者对学生的各項打分做了统计,平均分依次为9.12分、9.23分、9.29分、9.03分、8.73分、9.43分、8.94分、9.01分、9.18分、9.08分,总的平均分为91.04分. 在以后的教学中,教师要多注意数学思想的渗透,多督促学生记笔记.
学生打分后,教师还可以请某项得分特别低的学生来说明情况,提出自己的困惑. 在这节课上,笔者请了某项得分较低的学生来提出自己的困惑,他说,有时候他想不到解题方法,有时候他想到了又不敢把答案写上去. 这表明,该生还没有真正理解二次函数图象的对称性,还在把图象和点孤立开来.
师:二次函数y=ax2+bx+c(a≠0)的对称轴是什么?
生:直线x=-b/2a.
师:对称轴的本质是什么?
学生摇头.
师:对称轴的本质就是二次函数的图象关于这条直线对称. 那应用的关键是什么?
生:找到关于它对称的点.
师:对,换句话说,看到抛物线就要想到对称轴,只要是根据对称来的,就都是对的.
此处教师帮助学生巩固、完善知识,把握关键点.
最后,教师还可以在课后把评价表收起来,并单独辅导有困难的学生,同时反思自己的教学过程,力求不断调整教学以适应学生的学情.
教学反思
二次函数比较注重对学生学习能力和数学素养的考查,因此对大部分学生而言,难度较大. 本节课按照“微项目教学”单元复习范式,通过“用活动引出问题,用问题串联教学”来进行教学设计. 教师通过设置开放性问题来引导学生建立知识体系,让学生通过联想把新问题转化为用旧知识解决,在这个过程中,学生初步感知了用二次函数解决问题的重要思想——对称(数形结合). 在此基础上,学生自主完成了知识的迁移. 在这个环节,教师把学习的主动权还给学生,并通过问题引导,让他们充分地想和说.通过回顾本堂课的解题过程,学生从局部到整体地认识到了这类题的解题策略,并画出了解题的思维导图,同时梳理了解题过程中要用到的数学思想方法.
在整个教学过程中,教师做到了以下几点.
(1)以问题情境为抓手,在探究中注重对学生阅读能力、迁移能力的培养,促进学生深度理解. 虽然不同情境的侧重点不一样,但有共性,都沿着“理解—探究—应用”的思路展开,其中“理解”是基础,“探究”是过程,“应用”是目标.
(2)通过剖析解题思路的形成过程,引导学生学会“怎么想”. 在解题策略的小结和归纳中,教师帮助学生体会解此类题的通法,最后通过课后练习,对学习效果进行检测. 相信通过这节课的学习,学生以后处理二次函数问题会比较容易上手.
(3)关注学生在课堂上的参与度. 例题的安排有梯度,层层递进. 前面的问题起点低,每个层次的学生都能解决;后面的问题难度在递增,但教师强调需自己独立思考后再和其他学生讨论. 在课堂上,学生能讲的教师都要提供机会让他们讲. 对于学生不同的解法,只要合理,教师都要给予肯定,从而提升他们学习数学的自信心.
参考文献:
[1]孙雅琴. 初中数学课堂“微项目式学习”初探——以《平方差公式》一课为例[J]. 教育研究与评论(中学教育教学),2020(03):54-58.
[2]夏乾冬. 二次函数[J]. 中学数学教学参考,2021(02):49-51.
作者简介:范茜(1983—),硕士研究生,中学一级教师,从事初中数学教学研究工作.

